人教版九年级数学上册24.1.2-垂径定理的应用(用)1课件(共39张)
文档属性
| 名称 | 人教版九年级数学上册24.1.2-垂径定理的应用(用)1课件(共39张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 399.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 19:55:50 | ||
图片预览









文档简介
九年级数学(下)
圆
2. 圆对称性(2)
垂径定理的应用
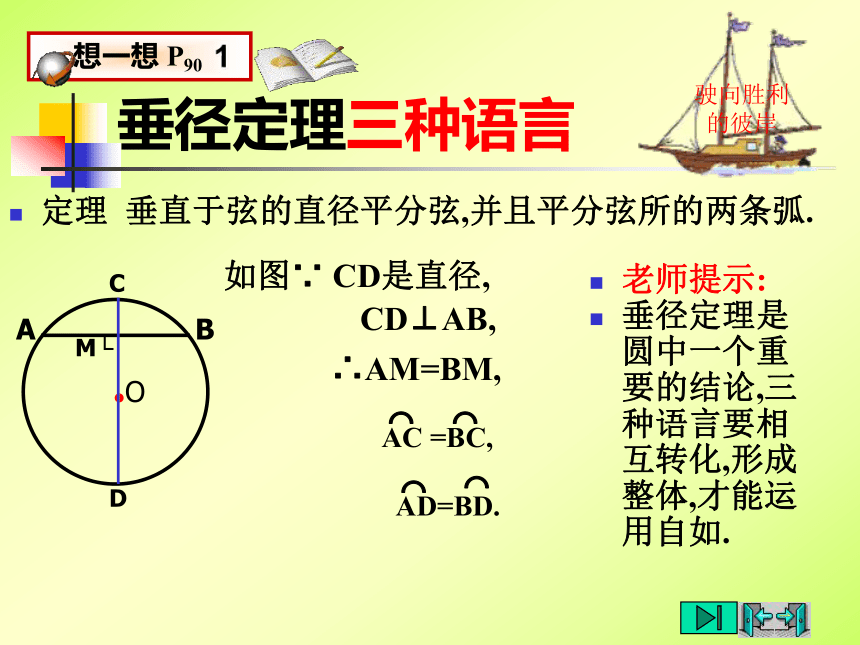
垂径定理三种语言
定理 垂直于弦的直径平分弦,并且平分弦所的两条弧.
老师提示:
垂径定理是圆中一个重要的结论,三种语言要相互转化,形成整体,才能运用自如.
想一想 P90
1
驶向胜利的彼岸
●O
A
B
C
D
M└
CD⊥AB,
如图∵ CD是直径,
∴AM=BM,
⌒
⌒
AC =BC,
⌒
⌒
AD=BD.
垂径定理的应用
例1 如图,一条公路的转变处是一段圆弧(即图中弧CD,点o是弧CD的圆心),其中CD=600m,E为弧CD上的一点,且oE⊥CD垂足为F,EF=90m.求这段弯路的半径.
想一想P91
2
驶向胜利的彼岸
解:连接oC.
●
O
C
D
E
F
┗
垂径定理三角形
对于一个圆中的弦长a、圆心到弦的距离d、圆半径r、弓形高h,这四个量中,只要已知其中任意两个量,就可以求出另外两个量.
想一想 P补
7
⑴d + h = r
⑵
已知:如图,直径CD⊥AB,垂足为E .
⑴若半径R = 2 ,AB = , 求OE、DE 的长.
⑵若半径R = 2 ,OE = 1 ,求AB、DE 的长.
⑶由⑴ 、⑵两题的启发,你还能编出什么其他问题?
例2、弓形的弦长为6cm,弓形的高为2cm,则这弓形所在的圆的半径为 .
变式:如下图,若以O为圆心再画一个圆交弦AB于C,D,则AC与BD间可能存在什么关系?
例3. 思考:过圆内一定点的弦中,
弦最短。
变式1:如图,P为⊙O内一点,且OP=2,⊙O的半径为3,则过P的最短的弦等于___________。
O
P
已知P为
内一点,且OP=2cm,如果
的半径是
,那么过P点的最短
的弦等于 .
例4.在直径为650mm的圆柱形油槽内装入一些油后,若油面宽AB = 600mm,求油的最大深度.
E
D
┌
600
情况1:
B
A
O
600
? 650
D
情况2:
已知:AB和CD是⊙O内的两条平行弦,,AB=6cm,CD=8cm,
⊙O的半径为5cm,
思考题:
(1)请根据题意画出符合条件的图形
(2)求出AB、与CD间的距离。
(1)
(2)
例5. 已知: (如图),求作: 的中点。
D
C
E
A
B
A
B
例5. 已知: (如图),求作: 的中点。
A
B
赵州石拱桥
1.1300多年前,我国隋朝建造的赵州石拱桥(如图)的桥拱是圆弧形,它的跨度(弧所对是弦的长)为 37.4 m,拱高(弧的中点到弦的距离,也叫弓形高)为7.2m,求桥拱的半径(精确到0.1m).
随堂练习P92
3
驶向胜利的彼岸
你是第一个告诉同学们解题方法和结果的吗?
赵州石拱桥
随堂练习P92
4
驶向胜利的彼岸
解:如图,用 表示桥拱, 所在圆的圆心为O,半径为Rm,
经过圆心O作弦AB的垂线OD,D为垂足,与 相交于点C.根
据垂径定理,D是AB的中点,C是 的中点,CD就是拱高.
由题设
在Rt△OAD中,由勾股定理,得
解得 R≈27.9(m).
答:赵州石拱桥的桥拱半径约为27.9m.
R
D
37.4
7.2
船能过拱桥吗
例6 . 如图,某地有一圆弧形拱桥,桥下水面宽为7.2米,拱顶高出水面2.4米.现有一艘宽3米、船舱顶部为长方形并高出水面2米的货船要经过这里,此货船能顺利通过这座拱桥吗?
相信自己能独立完成解答.
做一做P补
5
驶向胜利的彼岸
船能过拱桥吗
解:如图,用 表示桥拱, 所在圆的圆心为O,半径为Rm,
经过圆心O作弦AB的垂线OD,D为垂足,与 相交于点C.根
据垂径定理,D是AB的中点,C是 的中点,CD就是拱高.
由题设得
做一做P补
6
驶向胜利的彼岸
在Rt△OAD中,由勾股定理,得
解得 R≈3.9(m).
在Rt△ONH中,由勾股定理,得
∴此货船能顺利通过这座拱桥.
范例
例7、如图,在⊙O中,弦AB长8cm,
圆心O到AB的距离为3cm,求的⊙O
半径。
O
B
A
转化思想
圆的线段问题转化
为直角三角形问题
变式1:如上图,若以O为圆心再画一个圆交弦AB于C,D,则AC与BD间可能存在什么关系?
变式2:如下图,若将AB向下平移,当移到过圆心时,结论AC=BD还成立吗?
变式3:如图,设AO=BO,求证AC=BD。
B
O
A
C
D
变式3:如图,设AO=BO,求证AC=BD。
变式4:如图,设OC=OD,求证AC=BD。
A
O
B
C
D
变式4:如图,设OC=OD,求证AC=BD。
结束寄语
形成天才的决定因素应该是勤奋.
下课了!
再见
三、计算题:
已知:在⊙O中,弦AB⊥CD于P,⊙O的半径为5,AB=8,CD=6,
OE⊥AB,OF⊥CD。
求四边形OEPF的周长
4
3
5
5
3
4
例2、 已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C、D两点.
求证:AC=BD.
学生练习
已知:AB是⊙O直径,CD
是弦,AE⊥CD,BF⊥CD
求证:EC=DF
.
A
O
B
E
C
D
F
1. 如图,圆O中,AB,CD 是两条弦E,F分别是AB,CD的中点,EF过圆心O,CD?AB为什么?
F
A
B
C
D
E
.O
分析:
CD ? AB
?CFE=90 ?
?BEF=90 ?
OF?CD
OE ?AB
OF过圆心
OE过圆心
点F是CD中点
点E是AB中点
?CFE= ?BEF
2. 在我们生活中处处存在数学问题,比如:某村在村口建一个如图形状的门楼,半圆拱的圆心距地面2米,半径1.5米。现有一辆高2.9米,宽2.5米的集装箱卡车,问能通过这个门楼吗?要解决这个问题,必须运用圆的有关知识,
C
D
O
A
B
E
F
M
3.如图,不过圆心的直线L交⊙O 于CD,AB 是⊙O 直径。AE、BF分别垂直于CD,垂足是E、F。
求证:CE=DF
4.在直径为650mm的圆柱形油槽内装入一些油后,若油面宽AB = 600mm,求油的最大深度.
E
D
┌
600
情况1:
B
A
O
600
? 650
D
情况2:
例3:图示,在直角三角形ABO中,角O为直角,AO=6,BO=8,以O为圆心,OA为半径作圆,交AB与点C,求BC的长。
挑战自我填一填
1、判断:
⑴垂直于弦的直线平分这条弦,并且平分弦所对的两条弧. ( )
⑵平分弦所对的一条弧的直径一定平分这条弦所对的另一条弧. ( )
⑶经过弦的中点的直径一定垂直于弦.( )
⑷圆的两条弦所夹的弧相等,则这两条弦平行. ( )
⑸弦的垂直平分线一定平分这条弦所对的弧. ( )
挑战自我画一画
3、已知:如图,⊙O 中, AB为 弦,D为
AB 的中点,OC交AB 于D ,AB = 6cm ,
CD = 1cm. 求⊙O 的半径OA.
挑战自我画一画
4.如图,圆O与矩形ABCD交于E、F、G、H,EF=10,HG=6,AH=4.求BE的长.
·
A
B
C
D
0
E
F
G
H
巩固训练
判断下列说法的正误
①平分弧的直径必平分弧所对的弦
②平分弦的直线必垂直弦
③垂直于弦的直径平分这条弦
④平分弦的直径垂直于这条弦
⑤弦的垂直平分线是圆的直径
⑥平分弦所对的一条弧的直径必垂直这条弦
⑦在圆中,如果一条直线经过圆心且平分弦,
必平分此弦所对的弧
⑧分别过弦的三等分点作弦的垂线,将弦所对
的两条弧分别三等分
挑战自我
P93:习题3.2 1题
祝你成功!
独立作业P91
11
驶向胜利的彼岸
结束寄语
形成天才的决定因素应该是勤奋.
下课了!
再见
圆
2. 圆对称性(2)
垂径定理的应用
垂径定理三种语言
定理 垂直于弦的直径平分弦,并且平分弦所的两条弧.
老师提示:
垂径定理是圆中一个重要的结论,三种语言要相互转化,形成整体,才能运用自如.
想一想 P90
1
驶向胜利的彼岸
●O
A
B
C
D
M└
CD⊥AB,
如图∵ CD是直径,
∴AM=BM,
⌒
⌒
AC =BC,
⌒
⌒
AD=BD.
垂径定理的应用
例1 如图,一条公路的转变处是一段圆弧(即图中弧CD,点o是弧CD的圆心),其中CD=600m,E为弧CD上的一点,且oE⊥CD垂足为F,EF=90m.求这段弯路的半径.
想一想P91
2
驶向胜利的彼岸
解:连接oC.
●
O
C
D
E
F
┗
垂径定理三角形
对于一个圆中的弦长a、圆心到弦的距离d、圆半径r、弓形高h,这四个量中,只要已知其中任意两个量,就可以求出另外两个量.
想一想 P补
7
⑴d + h = r
⑵
已知:如图,直径CD⊥AB,垂足为E .
⑴若半径R = 2 ,AB = , 求OE、DE 的长.
⑵若半径R = 2 ,OE = 1 ,求AB、DE 的长.
⑶由⑴ 、⑵两题的启发,你还能编出什么其他问题?
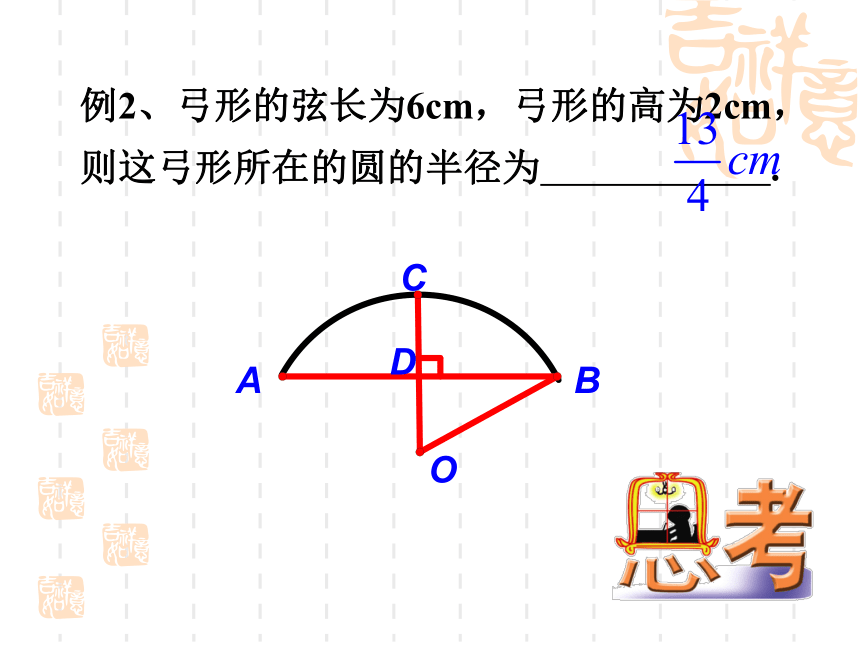
例2、弓形的弦长为6cm,弓形的高为2cm,则这弓形所在的圆的半径为 .
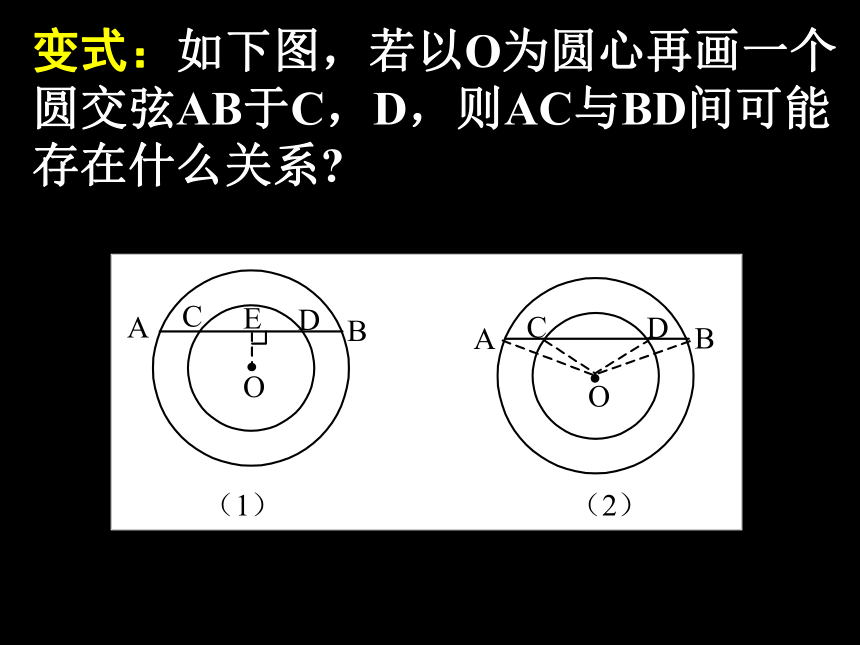
变式:如下图,若以O为圆心再画一个圆交弦AB于C,D,则AC与BD间可能存在什么关系?
例3. 思考:过圆内一定点的弦中,
弦最短。
变式1:如图,P为⊙O内一点,且OP=2,⊙O的半径为3,则过P的最短的弦等于___________。
O
P
已知P为
内一点,且OP=2cm,如果
的半径是
,那么过P点的最短
的弦等于 .
例4.在直径为650mm的圆柱形油槽内装入一些油后,若油面宽AB = 600mm,求油的最大深度.
E
D
┌
600
情况1:
B
A
O
600
? 650
D
情况2:
已知:AB和CD是⊙O内的两条平行弦,,AB=6cm,CD=8cm,
⊙O的半径为5cm,
思考题:
(1)请根据题意画出符合条件的图形
(2)求出AB、与CD间的距离。
(1)
(2)
例5. 已知: (如图),求作: 的中点。
D
C
E
A
B
A
B
例5. 已知: (如图),求作: 的中点。
A
B
赵州石拱桥
1.1300多年前,我国隋朝建造的赵州石拱桥(如图)的桥拱是圆弧形,它的跨度(弧所对是弦的长)为 37.4 m,拱高(弧的中点到弦的距离,也叫弓形高)为7.2m,求桥拱的半径(精确到0.1m).
随堂练习P92
3
驶向胜利的彼岸
你是第一个告诉同学们解题方法和结果的吗?
赵州石拱桥
随堂练习P92
4
驶向胜利的彼岸
解:如图,用 表示桥拱, 所在圆的圆心为O,半径为Rm,
经过圆心O作弦AB的垂线OD,D为垂足,与 相交于点C.根
据垂径定理,D是AB的中点,C是 的中点,CD就是拱高.
由题设
在Rt△OAD中,由勾股定理,得
解得 R≈27.9(m).
答:赵州石拱桥的桥拱半径约为27.9m.
R
D
37.4
7.2
船能过拱桥吗
例6 . 如图,某地有一圆弧形拱桥,桥下水面宽为7.2米,拱顶高出水面2.4米.现有一艘宽3米、船舱顶部为长方形并高出水面2米的货船要经过这里,此货船能顺利通过这座拱桥吗?
相信自己能独立完成解答.
做一做P补
5
驶向胜利的彼岸
船能过拱桥吗
解:如图,用 表示桥拱, 所在圆的圆心为O,半径为Rm,
经过圆心O作弦AB的垂线OD,D为垂足,与 相交于点C.根
据垂径定理,D是AB的中点,C是 的中点,CD就是拱高.
由题设得
做一做P补
6
驶向胜利的彼岸
在Rt△OAD中,由勾股定理,得
解得 R≈3.9(m).
在Rt△ONH中,由勾股定理,得
∴此货船能顺利通过这座拱桥.
范例
例7、如图,在⊙O中,弦AB长8cm,
圆心O到AB的距离为3cm,求的⊙O
半径。
O
B
A
转化思想
圆的线段问题转化
为直角三角形问题
变式1:如上图,若以O为圆心再画一个圆交弦AB于C,D,则AC与BD间可能存在什么关系?
变式2:如下图,若将AB向下平移,当移到过圆心时,结论AC=BD还成立吗?
变式3:如图,设AO=BO,求证AC=BD。
B
O
A
C
D
变式3:如图,设AO=BO,求证AC=BD。
变式4:如图,设OC=OD,求证AC=BD。
A
O
B
C
D
变式4:如图,设OC=OD,求证AC=BD。
结束寄语
形成天才的决定因素应该是勤奋.
下课了!
再见
三、计算题:
已知:在⊙O中,弦AB⊥CD于P,⊙O的半径为5,AB=8,CD=6,
OE⊥AB,OF⊥CD。
求四边形OEPF的周长
4
3
5
5
3
4
例2、 已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C、D两点.
求证:AC=BD.
学生练习
已知:AB是⊙O直径,CD
是弦,AE⊥CD,BF⊥CD
求证:EC=DF
.
A
O
B
E
C
D
F
1. 如图,圆O中,AB,CD 是两条弦E,F分别是AB,CD的中点,EF过圆心O,CD?AB为什么?
F
A
B
C
D
E
.O
分析:
CD ? AB
?CFE=90 ?
?BEF=90 ?
OF?CD
OE ?AB
OF过圆心
OE过圆心
点F是CD中点
点E是AB中点
?CFE= ?BEF
2. 在我们生活中处处存在数学问题,比如:某村在村口建一个如图形状的门楼,半圆拱的圆心距地面2米,半径1.5米。现有一辆高2.9米,宽2.5米的集装箱卡车,问能通过这个门楼吗?要解决这个问题,必须运用圆的有关知识,
C
D
O
A
B
E
F
M
3.如图,不过圆心的直线L交⊙O 于CD,AB 是⊙O 直径。AE、BF分别垂直于CD,垂足是E、F。
求证:CE=DF
4.在直径为650mm的圆柱形油槽内装入一些油后,若油面宽AB = 600mm,求油的最大深度.
E
D
┌
600
情况1:
B
A
O
600
? 650
D
情况2:
例3:图示,在直角三角形ABO中,角O为直角,AO=6,BO=8,以O为圆心,OA为半径作圆,交AB与点C,求BC的长。
挑战自我填一填
1、判断:
⑴垂直于弦的直线平分这条弦,并且平分弦所对的两条弧. ( )
⑵平分弦所对的一条弧的直径一定平分这条弦所对的另一条弧. ( )
⑶经过弦的中点的直径一定垂直于弦.( )
⑷圆的两条弦所夹的弧相等,则这两条弦平行. ( )
⑸弦的垂直平分线一定平分这条弦所对的弧. ( )
挑战自我画一画
3、已知:如图,⊙O 中, AB为 弦,D为
AB 的中点,OC交AB 于D ,AB = 6cm ,
CD = 1cm. 求⊙O 的半径OA.
挑战自我画一画
4.如图,圆O与矩形ABCD交于E、F、G、H,EF=10,HG=6,AH=4.求BE的长.
·
A
B
C
D
0
E
F
G
H
巩固训练
判断下列说法的正误
①平分弧的直径必平分弧所对的弦
②平分弦的直线必垂直弦
③垂直于弦的直径平分这条弦
④平分弦的直径垂直于这条弦
⑤弦的垂直平分线是圆的直径
⑥平分弦所对的一条弧的直径必垂直这条弦
⑦在圆中,如果一条直线经过圆心且平分弦,
必平分此弦所对的弧
⑧分别过弦的三等分点作弦的垂线,将弦所对
的两条弧分别三等分
挑战自我
P93:习题3.2 1题
祝你成功!
独立作业P91
11
驶向胜利的彼岸
结束寄语
形成天才的决定因素应该是勤奋.
下课了!
再见
同课章节目录
