人教版七年级上册数学第四章几何图形初步4.3.1角课件(共25张PPT)
文档属性
| 名称 | 人教版七年级上册数学第四章几何图形初步4.3.1角课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 825.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-15 06:29:52 | ||
图片预览




文档简介
4.3.1角
人教版七上
第四章几何图形初步
建筑上的应用
情境引入
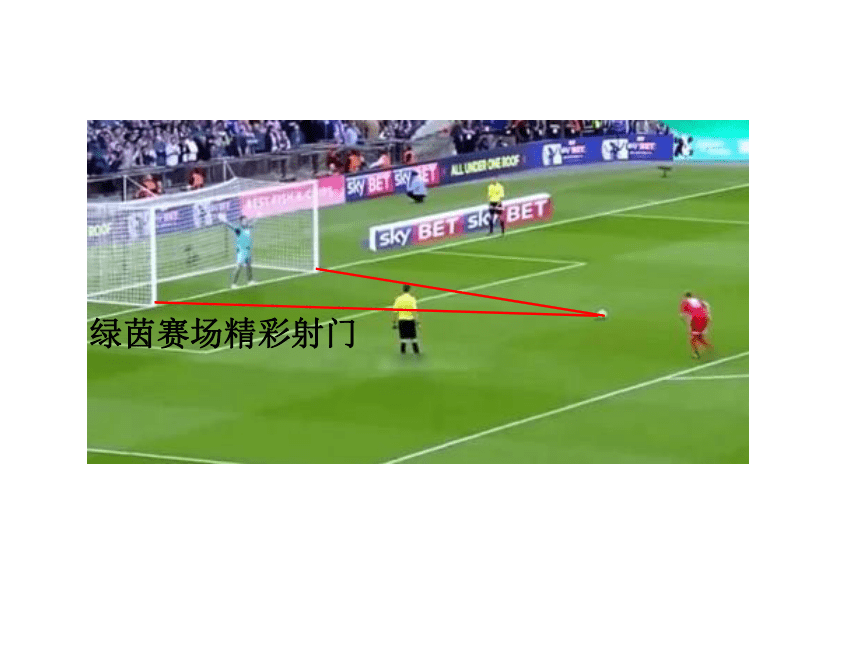
绿茵赛场精彩射门
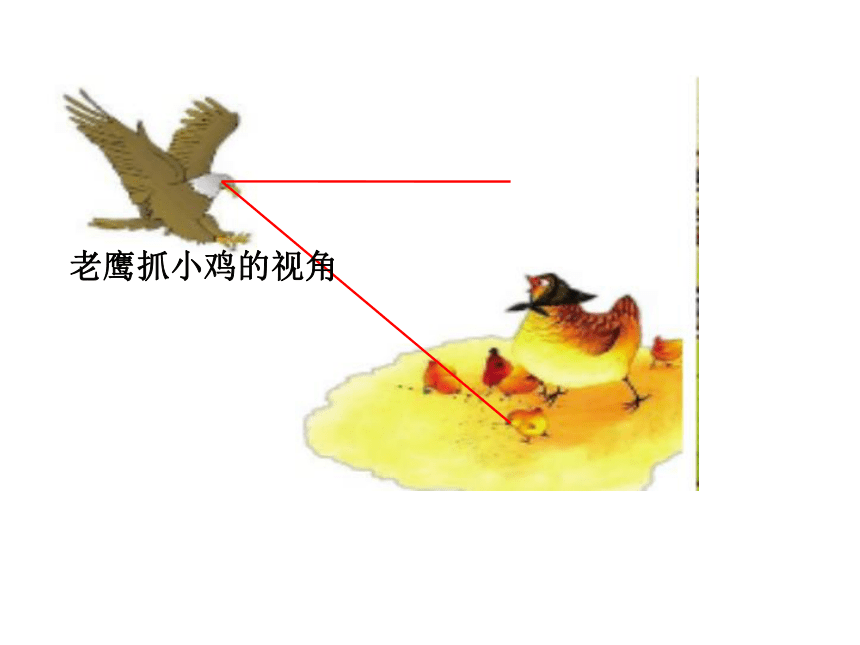
老鹰抓小鸡的视角
日常生活、学习工具等等
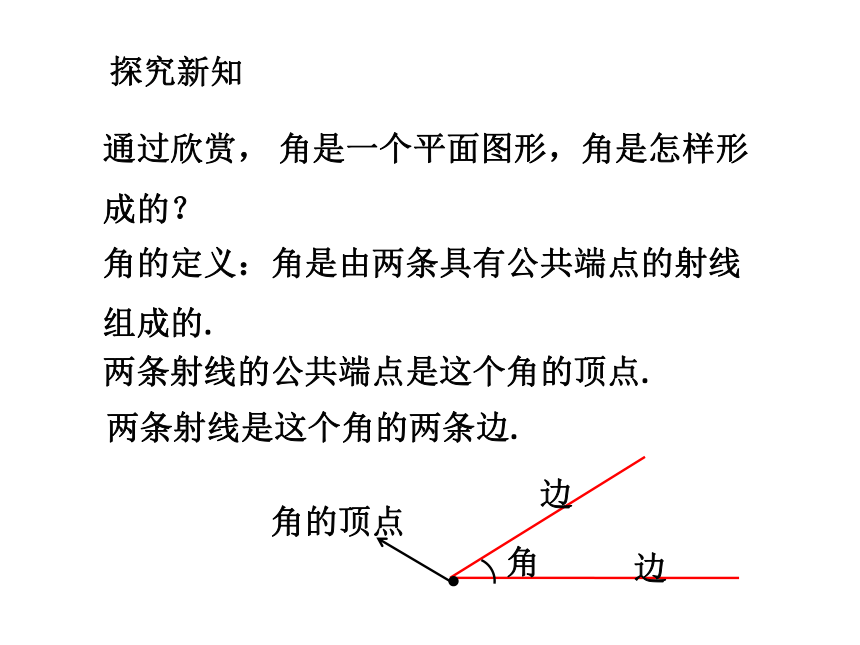
通过欣赏, 角是一个平面图形,角是怎样形成的?
角的定义:角是由两条具有公共端点的射线组成的.
两条射线的公共端点是这个角的顶点.
两条射线是这个角的两条边.
角的顶点
边
边
角
探究新知
角的表示方法:
1.用大写英文字母及符号“∠”来表示.
角的符号:用“∠”来表示角
(2)单独一个角可以用一个字母来表示.如:∠O.
A
B
O
(1)用三个字母及符号“∠”来表示.中间的字母表示顶点,其它两个字母分别表示角的两边上的点.如:∠ABC.
探究新知
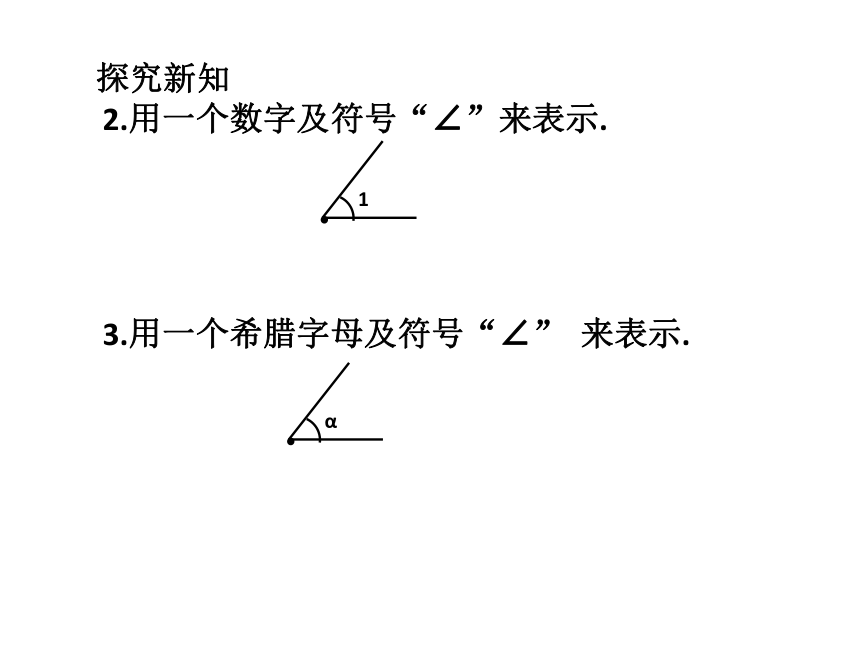
2.用一个数字及符号“∠”来表示.
1
3.用一个希腊字母及符号“∠” 来表示.
α
探究新知
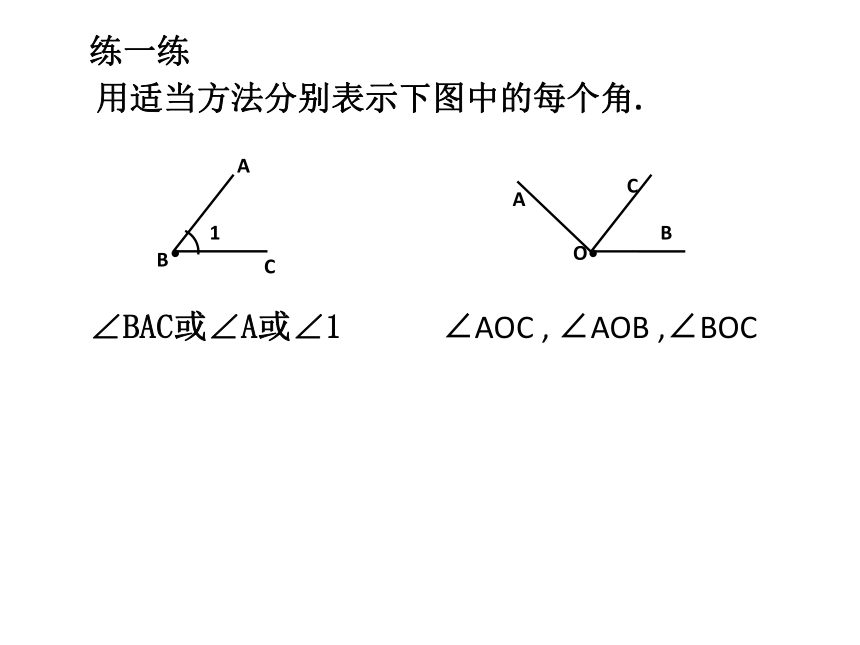
1
用适当方法分别表示下图中的每个角.
C
B
O
A
A
C
B
∠BAC或∠A或∠1
∠AOC , ∠AOB ,∠BOC
练一练
角也可以看做一条射线绕端点旋转所组成的图形。
角的另一个定义:
探究新知
1.角的定义一:
有公共端点的两条射线组成的图形叫做角,这个公共端点叫做角的顶点,这两条射线叫做角的边。
2.角的定义二:
角可以看成是一条射线绕着它的端点从一个位置旋转到另一个位置所形成的图形。射线旋转时经过的平面部分叫角的内部。
归纳总结
●
1.当终止位置OB和起始位置OA成90°时,形成直角。
∟
2.当终止位置OB和起始位置OA成一条直线时,形成平角。
●
继续旋转,OB和OA重合时,形成周角。
探究新知
角的度量单位:度 、分、秒.
度
分
秒
×60
×60
×3600
÷60
÷3600
÷60
1°的60分之一为1分,记作“1′”,即1°=60′
1′的60分之一为1秒,记作“1″”,即1′=60″
角的度量单位 及换算
探究新知
1.把以度为单位的化成度分秒表示
如:3.38°
=3°+(0.38×60) ′
=3°+22.8′
=3°+22 ′+(0.8 ×60) 〞
=3°+22′+48〞
探究新知
1.时针或分针走一圈=______
2.时针走一分钟对应的角度=____________
3.分针走一分钟对应的角度=______
4.分针走五分钟对应的角度=______
360°
30°
2 钟表上的时针、分针始终在围绕中心旋转,两针所成的夹角也随时间变化而变化。
0.5°
6°
探究新知
度、分、秒相互换算的法则
1.度、分、秒的换算是60进制.
2.角的度数的换算有两种情况:
(1)把度化成度、分、秒的形式,即从高单位向低单位转化时,每级变化乘以60.
(2)把度、分、秒化成度的形式,即从低单位向高单位转化时,每级变化除以60.
总结:
⑴1.45°等于多少分? 等于多少秒?
⑵1800″等于多少分? 等于多少度?
解: ⑴ 60′×1.45
=87′,
即 1.45°=87′=5220″.
⑵( ) ′× 1800=
1
60
30′,
60″×87
=5220″,
( ) ° × 30 =
1
60
0.5°,
即 1800″=30′=0.5°.
例1计算:
6°= ′= ″;
45.35°= ° ′;
2880″= ′= °
23°15′= °
360
21600
45
21
48
0.8
23.25
练一练:
1.把一个周角n等分,每份是30°,则n等于( )
A.9 B.10 C.11 D.12
2.下列说法中,正确的是( )
A.平角是一条直线
B.一直线是一个周角
C.两边成一条直线的角是平角
D.直线是平角
课堂演练:
D
C
3.如图,一共有( )个角
A
B
C
D
A 6 B 7 C 8 D 9
C
4.15时的钟表的时针与分针所形成的角的度数是( )
A.30° B.45°
C.60° D.90°
D
6. 比较32°18′ 32.18°.
(1).7.63°=_____度_____分_____秒.
(1).1.75°=_____分=_____秒.
5.(1) 20.6°= 度 分.
36
36
>
7
20
18
105
6300
7.如图,以O为顶点的角有几个,请分别把他们.
解:共有10个角,分别是:
∠AOB,∠AOC,∠AOD,∠AOE,∠BOC,∠BOD,∠BOE,∠COD,∠COE,∠DOE。
O
A
B
C
D
E
1.角的两种定义.
2.角的表示方法
3.平角、周角的概念
4.角的度量单位 及换算
课堂小结
课外作业
第134页第1、2题
人教版七上
第四章几何图形初步
建筑上的应用
情境引入
绿茵赛场精彩射门
老鹰抓小鸡的视角
日常生活、学习工具等等
通过欣赏, 角是一个平面图形,角是怎样形成的?
角的定义:角是由两条具有公共端点的射线组成的.
两条射线的公共端点是这个角的顶点.
两条射线是这个角的两条边.
角的顶点
边
边
角
探究新知
角的表示方法:
1.用大写英文字母及符号“∠”来表示.
角的符号:用“∠”来表示角
(2)单独一个角可以用一个字母来表示.如:∠O.
A
B
O
(1)用三个字母及符号“∠”来表示.中间的字母表示顶点,其它两个字母分别表示角的两边上的点.如:∠ABC.
探究新知
2.用一个数字及符号“∠”来表示.
1
3.用一个希腊字母及符号“∠” 来表示.
α
探究新知
1
用适当方法分别表示下图中的每个角.
C
B
O
A
A
C
B
∠BAC或∠A或∠1
∠AOC , ∠AOB ,∠BOC
练一练
角也可以看做一条射线绕端点旋转所组成的图形。
角的另一个定义:
探究新知
1.角的定义一:
有公共端点的两条射线组成的图形叫做角,这个公共端点叫做角的顶点,这两条射线叫做角的边。
2.角的定义二:
角可以看成是一条射线绕着它的端点从一个位置旋转到另一个位置所形成的图形。射线旋转时经过的平面部分叫角的内部。
归纳总结
●
1.当终止位置OB和起始位置OA成90°时,形成直角。
∟
2.当终止位置OB和起始位置OA成一条直线时,形成平角。
●
继续旋转,OB和OA重合时,形成周角。
探究新知
角的度量单位:度 、分、秒.
度
分
秒
×60
×60
×3600
÷60
÷3600
÷60
1°的60分之一为1分,记作“1′”,即1°=60′
1′的60分之一为1秒,记作“1″”,即1′=60″
角的度量单位 及换算
探究新知
1.把以度为单位的化成度分秒表示
如:3.38°
=3°+(0.38×60) ′
=3°+22.8′
=3°+22 ′+(0.8 ×60) 〞
=3°+22′+48〞
探究新知
1.时针或分针走一圈=______
2.时针走一分钟对应的角度=____________
3.分针走一分钟对应的角度=______
4.分针走五分钟对应的角度=______
360°
30°
2 钟表上的时针、分针始终在围绕中心旋转,两针所成的夹角也随时间变化而变化。
0.5°
6°
探究新知
度、分、秒相互换算的法则
1.度、分、秒的换算是60进制.
2.角的度数的换算有两种情况:
(1)把度化成度、分、秒的形式,即从高单位向低单位转化时,每级变化乘以60.
(2)把度、分、秒化成度的形式,即从低单位向高单位转化时,每级变化除以60.
总结:
⑴1.45°等于多少分? 等于多少秒?
⑵1800″等于多少分? 等于多少度?
解: ⑴ 60′×1.45
=87′,
即 1.45°=87′=5220″.
⑵( ) ′× 1800=
1
60
30′,
60″×87
=5220″,
( ) ° × 30 =
1
60
0.5°,
即 1800″=30′=0.5°.
例1计算:
6°= ′= ″;
45.35°= ° ′;
2880″= ′= °
23°15′= °
360
21600
45
21
48
0.8
23.25
练一练:
1.把一个周角n等分,每份是30°,则n等于( )
A.9 B.10 C.11 D.12
2.下列说法中,正确的是( )
A.平角是一条直线
B.一直线是一个周角
C.两边成一条直线的角是平角
D.直线是平角
课堂演练:
D
C
3.如图,一共有( )个角
A
B
C
D
A 6 B 7 C 8 D 9
C
4.15时的钟表的时针与分针所形成的角的度数是( )
A.30° B.45°
C.60° D.90°
D
6. 比较32°18′ 32.18°.
(1).7.63°=_____度_____分_____秒.
(1).1.75°=_____分=_____秒.
5.(1) 20.6°= 度 分.
36
36
>
7
20
18
105
6300
7.如图,以O为顶点的角有几个,请分别把他们.
解:共有10个角,分别是:
∠AOB,∠AOC,∠AOD,∠AOE,∠BOC,∠BOD,∠BOE,∠COD,∠COE,∠DOE。
O
A
B
C
D
E
1.角的两种定义.
2.角的表示方法
3.平角、周角的概念
4.角的度量单位 及换算
课堂小结
课外作业
第134页第1、2题
