人教版七年级上册数学4.3.3余角和补角课件(共21张PPT)
文档属性
| 名称 | 人教版七年级上册数学4.3.3余角和补角课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 91.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-15 06:31:57 | ||
图片预览



文档简介
4.3.3余角和补角
人教版七上
第四章几何图形初步
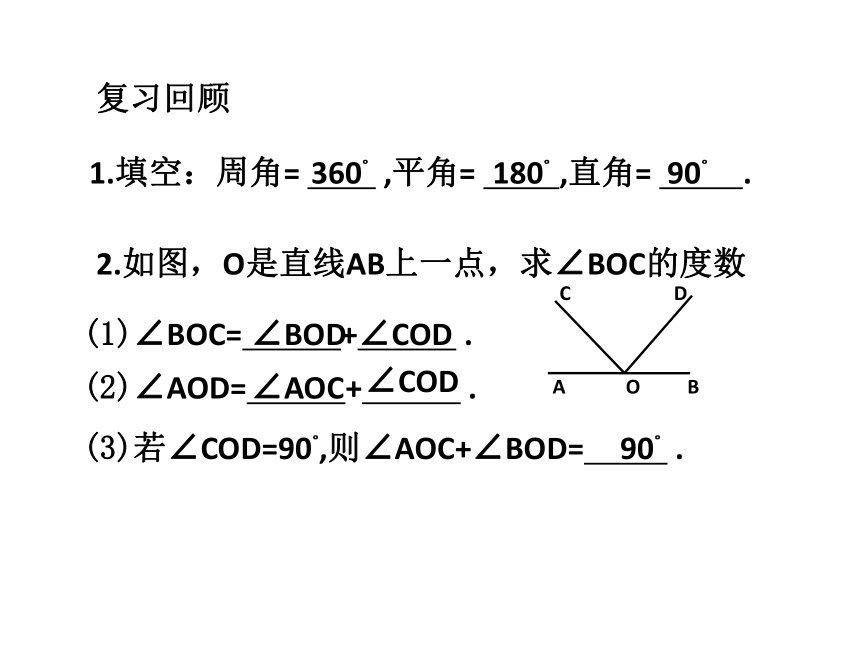
复习回顾
2.如图,O是直线AB上一点,求∠BOC的度数
1.填空:周角= ,平角= ,直角= .
O
A
B
C
D
(3)若∠COD=90?,则∠AOC+∠BOD= .
(1)∠BOC= + .
(2)∠AOD= + .
360?
180?
90?
∠COD
∠BOD
∠AOC
∠COD
90?
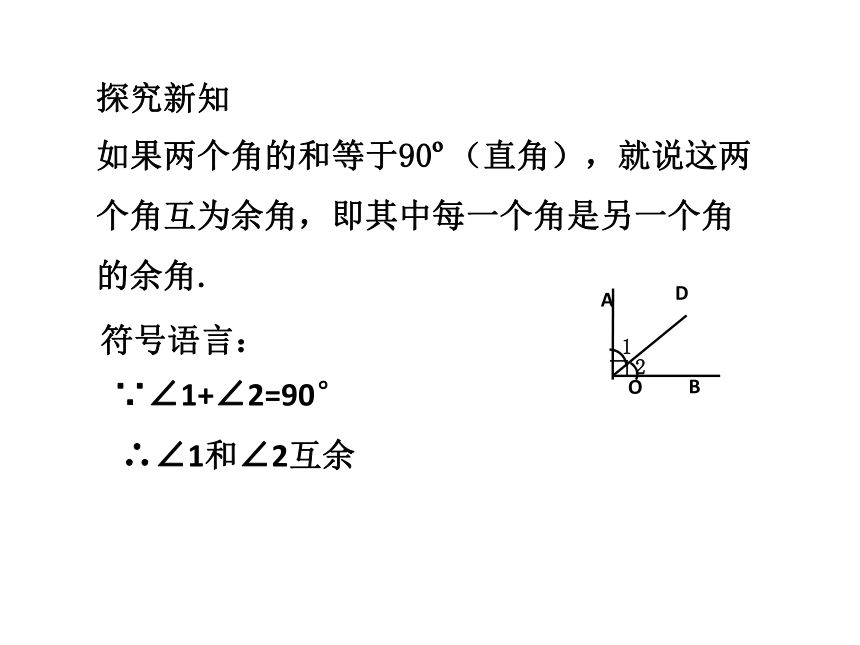
如果两个角的和等于90?(直角),就说这两个角互为余角,即其中每一个角是另一个角的余角.
∟
O
A
B
D
1
2
符号语言:
∵∠1+∠2=90°
∴∠1和∠2互余
探究新知
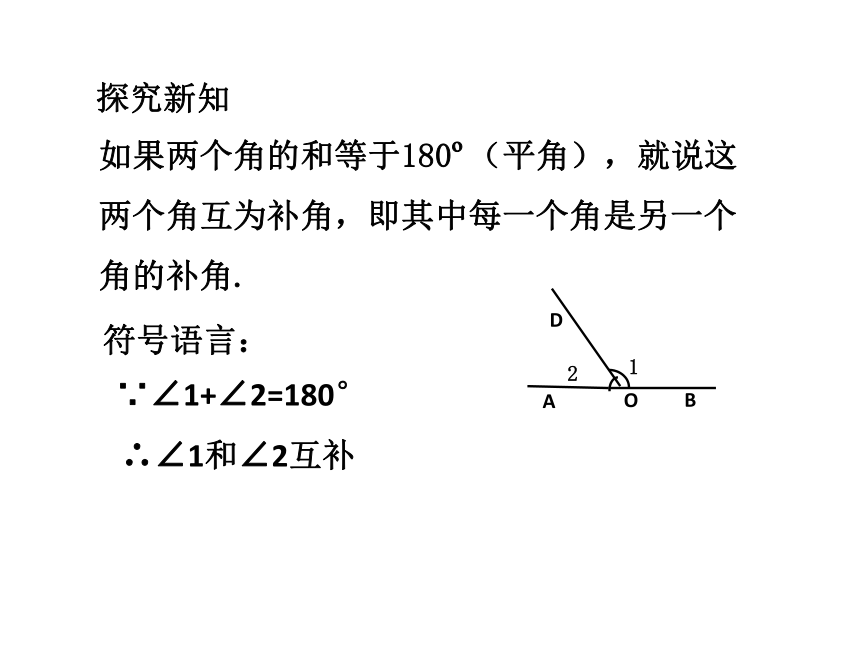
如果两个角的和等于180?(平角),就说这两个角互为补角,即其中每一个角是另一个角的补角.
O
A
B
D
1
2
符号语言:
∵∠1+∠2=180°
∴∠1和∠2互补
探究新知
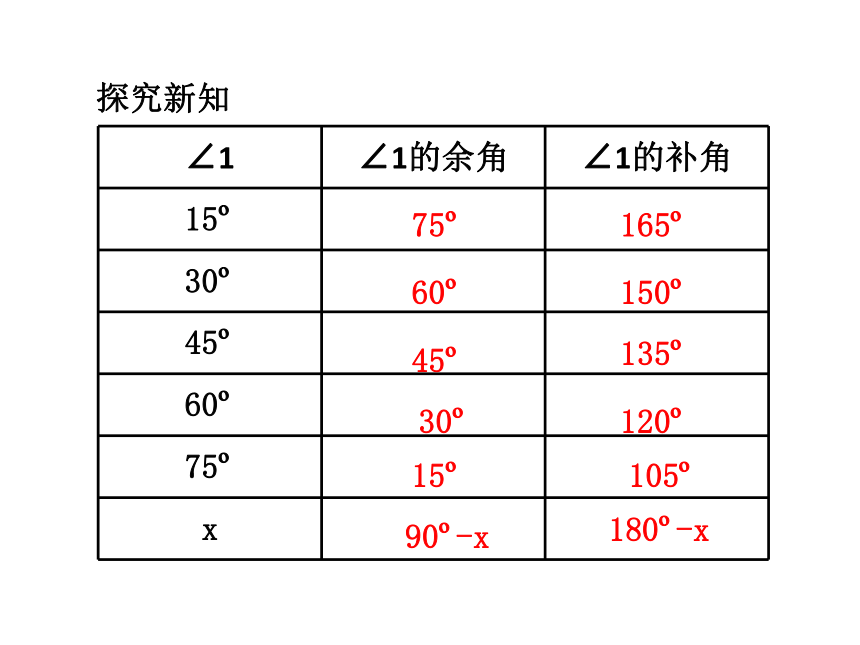
探究新知
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}∠1
∠1的余角
∠1的补角
15?
30?
45?
60?
75?
x
75?
165?
60?
150?
45?
135?
30?
120?
15?
105?
90?-x
180?-x
1.互余、互补都是反映两个角的数量关系,与角的位置无关.
2.互余的两角之和等于90°,其中任何一角都小于90°;互补的两角之和等于180°,其中的两角不可能都小于90°,也不可能都大于90°.
3.任何一个锐角的余角都小于它的补角
归纳
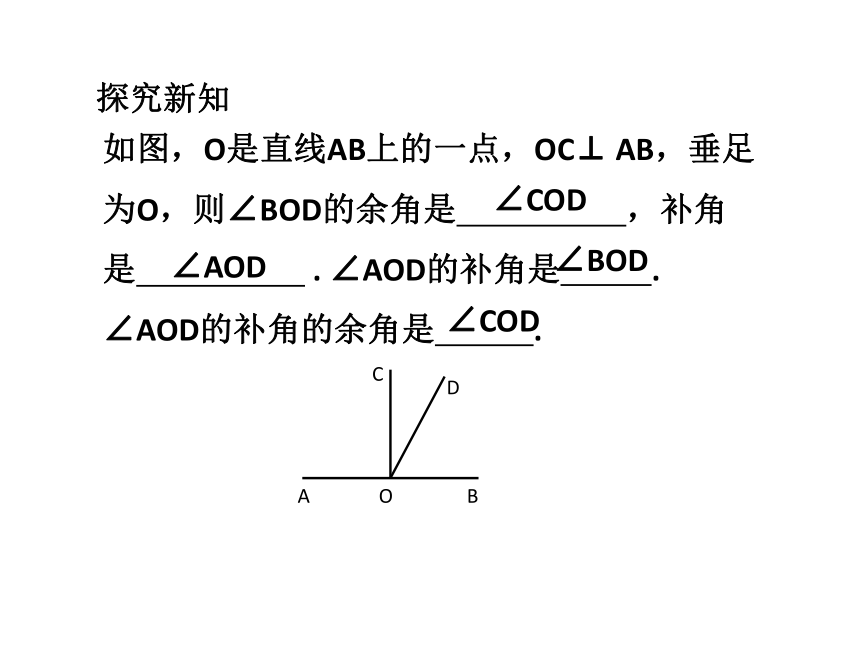
如图,O是直线AB上的一点,OC⊥ AB,垂足为O,则∠BOD的余角是 ,补角是 . ∠AOD的补角是 . ∠AOD的补角的余角是 .
A
B
C
D
O
∠COD
∠AOD
∠BOD
∠COD
探究新知
若一个角的补角等于它的余角的4倍,求这个角的度数。
解:设这个角是X度,则它°补角是(180-X),余角是(90-X),根据题意得:
180°-x=4(90°-x)
解得:
x=60°
这个角的度数是60°
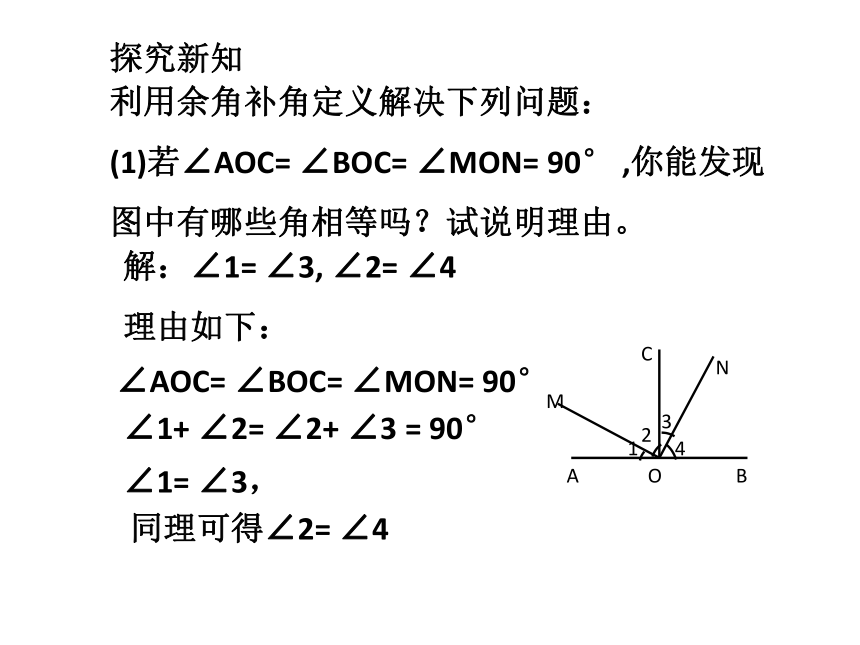
利用余角补角定义解决下列问题:
(1)若∠AOC= ∠BOC= ∠MON= 90° ,你能发现图中有哪些角相等吗?试说明理由。
A
B
C
N
O
M
1
2
3
4
∠AOC= ∠BOC= ∠MON= 90°
解:∠1= ∠3, ∠2= ∠4
理由如下:
∠1+ ∠2= ∠2+ ∠3 = 90°
∠1= ∠3,
同理可得∠2= ∠4
探究新知
(2)若直线AB与CD相交于点O ,你能发现图中有哪些角相等吗?试说明理由。
∠1= ∠3, ∠2= ∠4
A
B
C
O
D
1
2
3
4
∠1+ ∠2= ∠2+ ∠3 = 180°
∠1= ∠3,
同理可得∠2= ∠4
∠1+ ∠2= ∠2+ ∠3 = 90°
∠1= ∠3,
同角或等角的余角相等
余角的性质:
补角的性质:
同角或等角的补角相等
∠1+ ∠2= ∠2+ ∠3 = 180°
∠1= ∠3,
或∠1= ∠3,
∠2+ ∠1= ∠3+ ∠4 = 90°
A
B
C
N
O
M
1
2
3
4
∠2=∠4
A
B
C
O
D
1
2
3
4
方位角的定义:
以正北、正南的方向为基准,描述运动的方向,如图OA北偏东20°,OB为南偏东40°,这样的表示方向的角叫做方位角.
O
A
B
20°
40°
如图,射线OA表示北偏东 ,射线OB表示 ,射线OC表示 ,也叫 ,射线OD表示 .
O
A
B
30°
60°
C
D
45°
30°
南偏东30°
西南方向
南偏西45°
正西方向
1.若一个角为50°,则它的余角等于 .
A. 50° B. 40° C. 130° D. 60°
2.∠1和∠2互余,且∠1- ∠2= 30°,则∠1和∠2的度数分别为 .
60°、 30°
B
课堂练习
3.如果∠1+∠2=180°,而∠2与∠3互补,那么∠1与∠3的数量关系是________.
4.若一个角的3倍等于这个角的补角,则这个角等于________.
∠1=∠3
45°
5.如图,射线OA表示北偏东30°,画出表示下列方向的射线.
O
A
B
30°
30°
C
40°
(1).北偏西40°.
(3).南偏东30°.
(2).西南方向
北偏西
南偏东
西南方向
D
45°
6.如图,若直线AB与直线CD交于点O,OA平分∠COF,OE⊥CD.
(1)写出图中与∠EOB互余的角;
(2)若∠AOF=30°,求∠BOE和∠DOF的度数.
(1)解:∵OA平分∠COF, ∴∠COA=∠FOA=∠BOD,
∵OE⊥CD,
∴∠EOB+∠BOD=90°,
∴∠COA+∠EOB=90°,∠FOA+∠EOB=90°,
∴与∠EOB互余的角是:∠COA,∠FOA,∠BOD
(2)解:∵∠AOF=30°,由(1)知∠COA=∠FOA=∠BOD=30°, ∴∠DOF=180°﹣∠FOA﹣∠BOD=120°,
∵OE⊥CD,
∴∠BOE=90°﹣30°=60°
1.余角和补角的定义及其性质定理
2.方位角的定义
3.运用方程解决有关余角和补角的问题
课堂小结
探究新知
第139页
第6题、第8题
人教版七上
第四章几何图形初步
复习回顾
2.如图,O是直线AB上一点,求∠BOC的度数
1.填空:周角= ,平角= ,直角= .
O
A
B
C
D
(3)若∠COD=90?,则∠AOC+∠BOD= .
(1)∠BOC= + .
(2)∠AOD= + .
360?
180?
90?
∠COD
∠BOD
∠AOC
∠COD
90?
如果两个角的和等于90?(直角),就说这两个角互为余角,即其中每一个角是另一个角的余角.
∟
O
A
B
D
1
2
符号语言:
∵∠1+∠2=90°
∴∠1和∠2互余
探究新知
如果两个角的和等于180?(平角),就说这两个角互为补角,即其中每一个角是另一个角的补角.
O
A
B
D
1
2
符号语言:
∵∠1+∠2=180°
∴∠1和∠2互补
探究新知
探究新知
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}∠1
∠1的余角
∠1的补角
15?
30?
45?
60?
75?
x
75?
165?
60?
150?
45?
135?
30?
120?
15?
105?
90?-x
180?-x
1.互余、互补都是反映两个角的数量关系,与角的位置无关.
2.互余的两角之和等于90°,其中任何一角都小于90°;互补的两角之和等于180°,其中的两角不可能都小于90°,也不可能都大于90°.
3.任何一个锐角的余角都小于它的补角
归纳
如图,O是直线AB上的一点,OC⊥ AB,垂足为O,则∠BOD的余角是 ,补角是 . ∠AOD的补角是 . ∠AOD的补角的余角是 .
A
B
C
D
O
∠COD
∠AOD
∠BOD
∠COD
探究新知
若一个角的补角等于它的余角的4倍,求这个角的度数。
解:设这个角是X度,则它°补角是(180-X),余角是(90-X),根据题意得:
180°-x=4(90°-x)
解得:
x=60°
这个角的度数是60°
利用余角补角定义解决下列问题:
(1)若∠AOC= ∠BOC= ∠MON= 90° ,你能发现图中有哪些角相等吗?试说明理由。
A
B
C
N
O
M
1
2
3
4
∠AOC= ∠BOC= ∠MON= 90°
解:∠1= ∠3, ∠2= ∠4
理由如下:
∠1+ ∠2= ∠2+ ∠3 = 90°
∠1= ∠3,
同理可得∠2= ∠4
探究新知
(2)若直线AB与CD相交于点O ,你能发现图中有哪些角相等吗?试说明理由。
∠1= ∠3, ∠2= ∠4
A
B
C
O
D
1
2
3
4
∠1+ ∠2= ∠2+ ∠3 = 180°
∠1= ∠3,
同理可得∠2= ∠4
∠1+ ∠2= ∠2+ ∠3 = 90°
∠1= ∠3,
同角或等角的余角相等
余角的性质:
补角的性质:
同角或等角的补角相等
∠1+ ∠2= ∠2+ ∠3 = 180°
∠1= ∠3,
或∠1= ∠3,
∠2+ ∠1= ∠3+ ∠4 = 90°
A
B
C
N
O
M
1
2
3
4
∠2=∠4
A
B
C
O
D
1
2
3
4
方位角的定义:
以正北、正南的方向为基准,描述运动的方向,如图OA北偏东20°,OB为南偏东40°,这样的表示方向的角叫做方位角.
O
A
B
20°
40°
如图,射线OA表示北偏东 ,射线OB表示 ,射线OC表示 ,也叫 ,射线OD表示 .
O
A
B
30°
60°
C
D
45°
30°
南偏东30°
西南方向
南偏西45°
正西方向
1.若一个角为50°,则它的余角等于 .
A. 50° B. 40° C. 130° D. 60°
2.∠1和∠2互余,且∠1- ∠2= 30°,则∠1和∠2的度数分别为 .
60°、 30°
B
课堂练习
3.如果∠1+∠2=180°,而∠2与∠3互补,那么∠1与∠3的数量关系是________.
4.若一个角的3倍等于这个角的补角,则这个角等于________.
∠1=∠3
45°
5.如图,射线OA表示北偏东30°,画出表示下列方向的射线.
O
A
B
30°
30°
C
40°
(1).北偏西40°.
(3).南偏东30°.
(2).西南方向
北偏西
南偏东
西南方向
D
45°
6.如图,若直线AB与直线CD交于点O,OA平分∠COF,OE⊥CD.
(1)写出图中与∠EOB互余的角;
(2)若∠AOF=30°,求∠BOE和∠DOF的度数.
(1)解:∵OA平分∠COF, ∴∠COA=∠FOA=∠BOD,
∵OE⊥CD,
∴∠EOB+∠BOD=90°,
∴∠COA+∠EOB=90°,∠FOA+∠EOB=90°,
∴与∠EOB互余的角是:∠COA,∠FOA,∠BOD
(2)解:∵∠AOF=30°,由(1)知∠COA=∠FOA=∠BOD=30°, ∴∠DOF=180°﹣∠FOA﹣∠BOD=120°,
∵OE⊥CD,
∴∠BOE=90°﹣30°=60°
1.余角和补角的定义及其性质定理
2.方位角的定义
3.运用方程解决有关余角和补角的问题
课堂小结
探究新知
第139页
第6题、第8题
