人教版数学九年级下册:28.1 锐角三角函数-课件(15张)
文档属性
| 名称 | 人教版数学九年级下册:28.1 锐角三角函数-课件(15张) |  | |
| 格式 | ppt | ||
| 文件大小 | 698.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 20:49:13 | ||
图片预览






文档简介
人教版九年级数学(下册)第二十八章
§28.1 锐角三角函数(2)
——余弦、正切
复习与探究:
1.锐角正弦的定义
在 中,
∠A的正弦:
2、当锐角A确定时,∠A的对边与斜边的比就随之确定。此时,其他边之间的比是否也随之确定?
新知探索:
1、当锐角A确定时,∠A的邻边与斜边的比, ∠A的对边与邻边的比也随之确定吗?为什么?说出理由。
方法一:从特殊到一般,仿照正弦的研究过程
方法二:根据相似三角形的性质来说明。
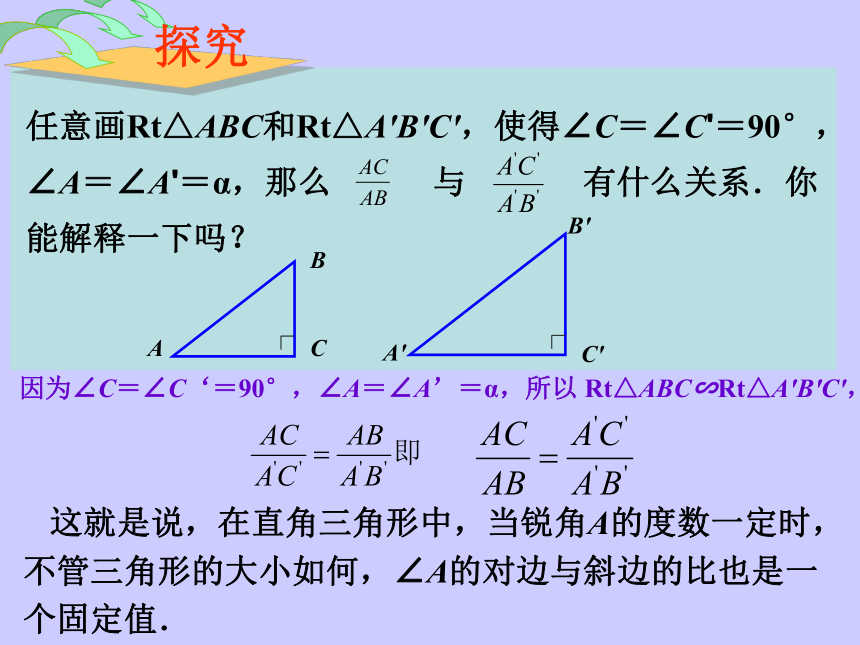
这就是说,在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比也是一个固定值.
任意画Rt△ABC和Rt△A'B'C',使得∠C=∠C'=90°,∠A=∠A'=α,那么 与 有什么关系.你能解释一下吗?
探究
A
B
C
A'
B'
C'
因为∠C=∠C‘=90°,∠A=∠A’=α,所以 Rt△ABC∽Rt△A'B'C',
如图,在Rt△ABC中,∠C=90°,
A
B
C
斜边c
对边a
邻边b
★我们把锐角A的邻边与斜边的比叫做∠A的余弦,记作cosA, 即
★我们把锐角A的对边与邻边的比叫做∠A的正切,记作tanA, 即
注意
cosA,tanA是一个完整的符号,它表示∠A的余弦、正切,记号里习惯省去角的符“∠”;
cosA,tanA没有单位,它表示一个比值,即直角三角形中∠A的邻边与斜边的比、对边与邻边的比;
cosA不表示“cos”乘以“A”, tanA不表示“tan”乘以“A”
对于锐角A的每一个确定的值,sinA有唯一确定的值与它对应,所以sinA是A的函数。
同样地,cosA,tanA也是A的函数。
锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.
例1 如图,在Rt△ABC中,∠C=90°BC=2,AB=3,求∠A,∠B的正弦、余弦、正切值.
A
B
C
2
3
延伸:由上面的计算,你能猜想∠A,∠B的正弦、余弦值有什么规律吗?
结论:一个锐角的正弦等于它余角的余弦,或一个锐角的余弦等于它余角的正弦。
解: 中,由勾股定理得:
A
B
C
6
例2 如图,在Rt△ABC中,∠C=90°,BC=6, ,求cosA和tanB的值.
1、下图中∠ACB=90°,CD⊥AB,垂足为D.指出∠A和∠B的对边、邻边.
练习:
A
B
C
D
(1) sinA =
=
AC
( )
BC
( )
(3) sinB=
=
AB
( )
CD
( )
CD
AB
BC
AC
(2) cosA =
=
AC
( )
AC
( )
(4) cosB=
=
AB
( )
BD
( )
AD
AB
BC
BC
2、分别求出下列直角三角形中两个锐角的正弦值、余弦值和正切值.
解:由勾股定理可知:
BC=5
解:由勾股定理可知:
AB=
1、在Rt△ABC中,如果各边长都扩大2倍,
那么锐角的正弦值、余弦值和正切值有什么
变化?
提高训练:
2、如图,为了测量河两岸A、B两点的距离,
在与AB垂直的方向点C处测得AC=a,∠ACB=α,
那么AB等于( )
a·sinα B. a·tanα
C. a·cosα D.
A
B
C
a
?
B
3、如图,在Rt△ABC中,∠C=90°,CD⊥AB于D。求出∠BCD的三个锐角三角函数值。
在Rt△ABC中,∠C=90°,我们把:
sin A=
cos A=
tan A=
分别叫做锐角∠A的正弦、余弦、正切、,统称为锐角∠A的锐角三角函数.
小 结
0<sin A<1,0<cos A<1
§28.1 锐角三角函数(2)
——余弦、正切
复习与探究:
1.锐角正弦的定义
在 中,
∠A的正弦:
2、当锐角A确定时,∠A的对边与斜边的比就随之确定。此时,其他边之间的比是否也随之确定?
新知探索:
1、当锐角A确定时,∠A的邻边与斜边的比, ∠A的对边与邻边的比也随之确定吗?为什么?说出理由。
方法一:从特殊到一般,仿照正弦的研究过程
方法二:根据相似三角形的性质来说明。
这就是说,在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比也是一个固定值.
任意画Rt△ABC和Rt△A'B'C',使得∠C=∠C'=90°,∠A=∠A'=α,那么 与 有什么关系.你能解释一下吗?
探究
A
B
C
A'
B'
C'
因为∠C=∠C‘=90°,∠A=∠A’=α,所以 Rt△ABC∽Rt△A'B'C',
如图,在Rt△ABC中,∠C=90°,
A
B
C
斜边c
对边a
邻边b
★我们把锐角A的邻边与斜边的比叫做∠A的余弦,记作cosA, 即
★我们把锐角A的对边与邻边的比叫做∠A的正切,记作tanA, 即
注意
cosA,tanA是一个完整的符号,它表示∠A的余弦、正切,记号里习惯省去角的符“∠”;
cosA,tanA没有单位,它表示一个比值,即直角三角形中∠A的邻边与斜边的比、对边与邻边的比;
cosA不表示“cos”乘以“A”, tanA不表示“tan”乘以“A”
对于锐角A的每一个确定的值,sinA有唯一确定的值与它对应,所以sinA是A的函数。
同样地,cosA,tanA也是A的函数。
锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.
例1 如图,在Rt△ABC中,∠C=90°BC=2,AB=3,求∠A,∠B的正弦、余弦、正切值.
A
B
C
2
3
延伸:由上面的计算,你能猜想∠A,∠B的正弦、余弦值有什么规律吗?
结论:一个锐角的正弦等于它余角的余弦,或一个锐角的余弦等于它余角的正弦。
解: 中,由勾股定理得:
A
B
C
6
例2 如图,在Rt△ABC中,∠C=90°,BC=6, ,求cosA和tanB的值.
1、下图中∠ACB=90°,CD⊥AB,垂足为D.指出∠A和∠B的对边、邻边.
练习:
A
B
C
D
(1) sinA =
=
AC
( )
BC
( )
(3) sinB=
=
AB
( )
CD
( )
CD
AB
BC
AC
(2) cosA =
=
AC
( )
AC
( )
(4) cosB=
=
AB
( )
BD
( )
AD
AB
BC
BC
2、分别求出下列直角三角形中两个锐角的正弦值、余弦值和正切值.
解:由勾股定理可知:
BC=5
解:由勾股定理可知:
AB=
1、在Rt△ABC中,如果各边长都扩大2倍,
那么锐角的正弦值、余弦值和正切值有什么
变化?
提高训练:
2、如图,为了测量河两岸A、B两点的距离,
在与AB垂直的方向点C处测得AC=a,∠ACB=α,
那么AB等于( )
a·sinα B. a·tanα
C. a·cosα D.
A
B
C
a
?
B
3、如图,在Rt△ABC中,∠C=90°,CD⊥AB于D。求出∠BCD的三个锐角三角函数值。
在Rt△ABC中,∠C=90°,我们把:
sin A=
cos A=
tan A=
分别叫做锐角∠A的正弦、余弦、正切、,统称为锐角∠A的锐角三角函数.
小 结
0<sin A<1,0<cos A<1
