人教版数学九年级下册:28.2.2应用举例-课件(22张)
文档属性
| 名称 | 人教版数学九年级下册:28.2.2应用举例-课件(22张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 36.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 20:44:15 | ||
图片预览








文档简介
展
题
说
示
2020年4月
录
目
说题意
01
说思路
02
说总结
03
说推广
04
说设计
05
节
环
说题意
Part One
(人教版九年级数学下册第28章锐角三角函数中75页例4)
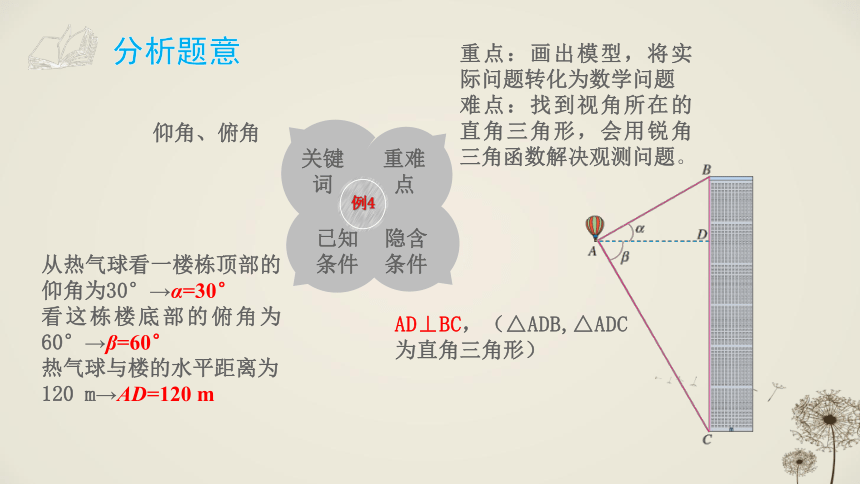
例4 热气球的探测器显示,从热气球看一栋楼顶部的仰角为 30°,看这栋楼底部的俯角为 60°,热气球与楼的水平距离为 120 m,这栋楼有多高(结果取整数)?
本题是与视角有关的解直角三角形的实际应用,即适当选用与视角有关角的锐角三角函数解直角三角形。此类型问题在2016,2017,2018年新疆中考数学卷中均有出现,《数学课程标准》中明确指出:能用锐角三角函数解直角三角形,能用相关知识解决一些简单的实际问题。所以指导学生理清由实际问题转化为锐角三角函数模型的思路,帮助学生攻克中考重要考点是十分必要的。
这道题是面向中考第一轮复习的九年级学生,他们已经学会了利用锐角三角函数解直角三角形,但不少学生对实际问题中,与视角有关角的锐角三角函数解直角三角形问题仍无从下手,导致做题时失分情况严重。
根据教学大纲要求,学生对此内容认知特点确定目标:
理解利用视角解直角三角形的数学依据
会用与视角有关角的锐角三角函数解直角三角形
能将实际问题转化为锐角三角函数模型
1
2
3
节
环
说思路
Part Tow
例4
从热气球看一楼栋顶部的仰角为30°→α=30°
看这栋楼底部的俯角为60°→β=60°
热气球与楼的水平距离为 120 m→AD=120 m
仰角、俯角
AD⊥BC,(△ADB,△ADC为直角三角形)
重点:画出模型,将实际问题转化为数学问题
难点:找到视角所在的直角三角形,会用锐角三角函数解决观测问题。
解:如图,α=30°,β=60°,AD=120.
∵ tanα= ,tanβ= .
∴ BD=AD·tanα=120×tan 30°
=120× = ,
CD=AD·tanβ=120×tan 60°
=120× = .
∴ BC=BD+CD= +
= ≈277(m).
A
α
β
D
C
B
(1)
(2)
仰角、俯角分不清楚
没有利用隐含条件AD⊥BC.
在△BAC中,求边BC。(没有已知边长,缺条件,无法解决)
A
α
β
D
C
B
节
环
说总结
Part Three
(1)
(2)
(3)
(4)
适当选用与视角有关角的锐角三角函数等解直角三角形(解多次直角三角形)
同一视点的仰俯角问题的解决方法:
得到数学问题的答案
得到实际问题的答案
将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题)
根据问题中的条件,找到视角所在的直角三角形
(通常过视点延长水平线构造直角三角形)
节
环
说推广
Part Four
(2018新疆中考)20.如图,在数学活动课上,小丽为了测量校园内旗杆 AB 的高度,站在教学楼的 C 处测得旗杆底端 B 的俯角为45°,测得旗杆顶端 A 的仰角为30°,已知旗杆与教学楼的距离 BD=9m,请你帮她求出旗杆的高度(结果保留根号).
析:根据问题中的条件,找到视角所在的直角三角形
(过视点延长水平线)
A
B
D
C
30°
45°
1.同一视点的仰俯角
(课本76页)1.如图,建筑物BC上有一旗杆AB,从与 BC 相距 40m 的 D 处观测旗杆顶部 A 的仰角为50°,观测旗杆底部 B 的仰角为45°求旗杆的高度(结果保留小数点后一位).
析:根据问题中的条件,找到视角所在的直角三角形
(隐含条件为AC⊥DC即△ACD,△BCD为直角三角形)
(课本84页)8.如图,两建筑物的水平距离BC为32.6 m, 从A点测得D点的俯角α为30°,测得C点的俯角β为45°,求这两个建筑物的高度(结果保留根号).
析:根据问题中的条件,找到视角所在的直角三角形
(过视线上的点向水平线引垂线构造直角三角形)
(课本84页)9.某型号飞机的机翼形状如图所示.根据图中数据计算AC,BD和AB的长度(结果保留小数点后两位).
析:把此题看成与视角有关的解直角三角形问题,
点C点D为视点。
(2017新疆中考)19.如图,甲、乙为两座建筑物,他们之间的水平距离 BC 为30m,在 A 点测得 D点的仰角∠EAD为45°,在 B 点测得 D 点的仰角∠CBD 为60°,求这两座建筑物的高度,(结果保留根号)
45°
60°
A
甲
乙
B
D
C
小试牛刀
析:根据问题中的条件,找到视角所在的直角三角形
(过视点延长水平线)
节
环
说设计
Part Five
与视角有关的解直角三角形的实际应用
画 画出平面图形
找 找到视角所在的直角三角形
1 通常过视点延长水平线构造直角三角形
2 过视线上的点向水平线引垂线构造直角三角形
解 解多次直角三角形
得 得到实际问题的答案
谢谢观看!
题
说
示
2020年4月
录
目
说题意
01
说思路
02
说总结
03
说推广
04
说设计
05
节
环
说题意
Part One
(人教版九年级数学下册第28章锐角三角函数中75页例4)
例4 热气球的探测器显示,从热气球看一栋楼顶部的仰角为 30°,看这栋楼底部的俯角为 60°,热气球与楼的水平距离为 120 m,这栋楼有多高(结果取整数)?
本题是与视角有关的解直角三角形的实际应用,即适当选用与视角有关角的锐角三角函数解直角三角形。此类型问题在2016,2017,2018年新疆中考数学卷中均有出现,《数学课程标准》中明确指出:能用锐角三角函数解直角三角形,能用相关知识解决一些简单的实际问题。所以指导学生理清由实际问题转化为锐角三角函数模型的思路,帮助学生攻克中考重要考点是十分必要的。
这道题是面向中考第一轮复习的九年级学生,他们已经学会了利用锐角三角函数解直角三角形,但不少学生对实际问题中,与视角有关角的锐角三角函数解直角三角形问题仍无从下手,导致做题时失分情况严重。
根据教学大纲要求,学生对此内容认知特点确定目标:
理解利用视角解直角三角形的数学依据
会用与视角有关角的锐角三角函数解直角三角形
能将实际问题转化为锐角三角函数模型
1
2
3
节
环
说思路
Part Tow
例4
从热气球看一楼栋顶部的仰角为30°→α=30°
看这栋楼底部的俯角为60°→β=60°
热气球与楼的水平距离为 120 m→AD=120 m
仰角、俯角
AD⊥BC,(△ADB,△ADC为直角三角形)
重点:画出模型,将实际问题转化为数学问题
难点:找到视角所在的直角三角形,会用锐角三角函数解决观测问题。
解:如图,α=30°,β=60°,AD=120.
∵ tanα= ,tanβ= .
∴ BD=AD·tanα=120×tan 30°
=120× = ,
CD=AD·tanβ=120×tan 60°
=120× = .
∴ BC=BD+CD= +
= ≈277(m).
A
α
β
D
C
B
(1)
(2)
仰角、俯角分不清楚
没有利用隐含条件AD⊥BC.
在△BAC中,求边BC。(没有已知边长,缺条件,无法解决)
A
α
β
D
C
B
节
环
说总结
Part Three
(1)
(2)
(3)
(4)
适当选用与视角有关角的锐角三角函数等解直角三角形(解多次直角三角形)
同一视点的仰俯角问题的解决方法:
得到数学问题的答案
得到实际问题的答案
将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题)
根据问题中的条件,找到视角所在的直角三角形
(通常过视点延长水平线构造直角三角形)
节
环
说推广
Part Four
(2018新疆中考)20.如图,在数学活动课上,小丽为了测量校园内旗杆 AB 的高度,站在教学楼的 C 处测得旗杆底端 B 的俯角为45°,测得旗杆顶端 A 的仰角为30°,已知旗杆与教学楼的距离 BD=9m,请你帮她求出旗杆的高度(结果保留根号).
析:根据问题中的条件,找到视角所在的直角三角形
(过视点延长水平线)
A
B
D
C
30°
45°
1.同一视点的仰俯角
(课本76页)1.如图,建筑物BC上有一旗杆AB,从与 BC 相距 40m 的 D 处观测旗杆顶部 A 的仰角为50°,观测旗杆底部 B 的仰角为45°求旗杆的高度(结果保留小数点后一位).
析:根据问题中的条件,找到视角所在的直角三角形
(隐含条件为AC⊥DC即△ACD,△BCD为直角三角形)
(课本84页)8.如图,两建筑物的水平距离BC为32.6 m, 从A点测得D点的俯角α为30°,测得C点的俯角β为45°,求这两个建筑物的高度(结果保留根号).
析:根据问题中的条件,找到视角所在的直角三角形
(过视线上的点向水平线引垂线构造直角三角形)
(课本84页)9.某型号飞机的机翼形状如图所示.根据图中数据计算AC,BD和AB的长度(结果保留小数点后两位).
析:把此题看成与视角有关的解直角三角形问题,
点C点D为视点。
(2017新疆中考)19.如图,甲、乙为两座建筑物,他们之间的水平距离 BC 为30m,在 A 点测得 D点的仰角∠EAD为45°,在 B 点测得 D 点的仰角∠CBD 为60°,求这两座建筑物的高度,(结果保留根号)
45°
60°
A
甲
乙
B
D
C
小试牛刀
析:根据问题中的条件,找到视角所在的直角三角形
(过视点延长水平线)
节
环
说设计
Part Five
与视角有关的解直角三角形的实际应用
画 画出平面图形
找 找到视角所在的直角三角形
1 通常过视点延长水平线构造直角三角形
2 过视线上的点向水平线引垂线构造直角三角形
解 解多次直角三角形
得 得到实际问题的答案
谢谢观看!
