湘教版(2012)初中数学七年级上册4.3.1 角与角的大小比较 课件(28张)
文档属性
| 名称 | 湘教版(2012)初中数学七年级上册4.3.1 角与角的大小比较 课件(28张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 714.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 20:43:20 | ||
图片预览








文档简介
房顶的角
吊扇扇叶的夹角
剪刀的角
人仰视时的视角
楼梯的折角
时针和分针的夹角
角与角的大小比较
学习目标:
1.掌握角的概念和角的表示方法
2.掌握角的大小比较的方法
3.掌握角平分线的定义
问题导学(阅读教材P123-125,思考下列问题)
1.角的定义是什么?
2.什么是平角?什么是周角?
3.角有哪些表示方法?用这些方法表示角时要注意哪些地方?
4.如何比较两个角的大小?你有哪些方法?
5.角平分线是怎样定义的?
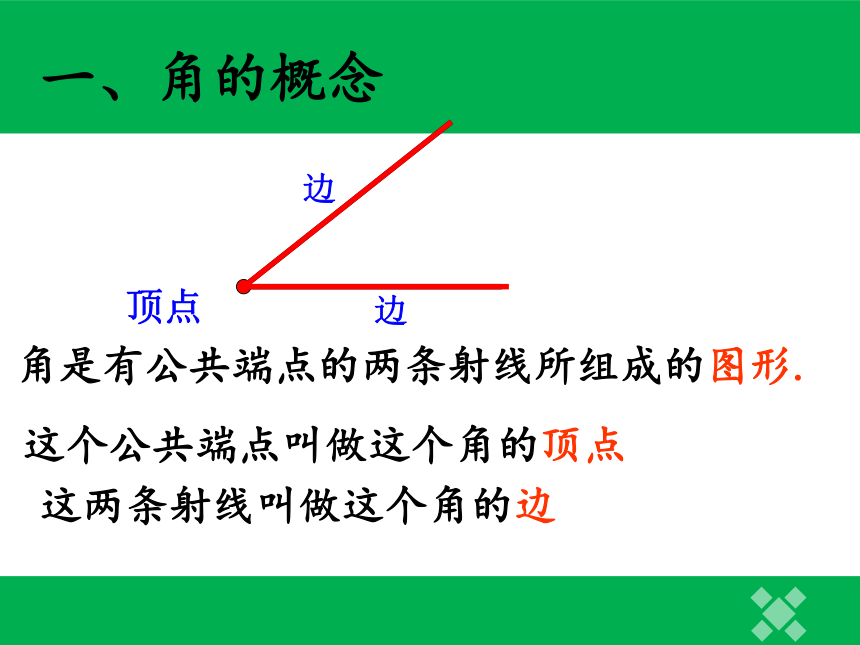
角是有公共端点的两条射线所组成的图形.
这个公共端点叫做这个角的顶点
这两条射线叫做这个角的边
一、角的概念
顶点
边
边
动态的观点
角也可以看成是一条射线绕着它的端点旋转而成的图形.
顶点
始边
起始位置的射线叫做这个角的始边
终边
终止位置的射线叫做这个角的终边
始边旋转到终边所扫过的区域,
叫角的内部
O
A
B
当射线绕着端点旋转到与原来的位置在同一直线上但方向相反时,所成的角叫做平角.
二、平角与周角
O
A
(B)
当射线绕着端点旋转一周,又回到原来的位置时,所成的角叫做周角.
三、角的表示方法
{C4B1156A-380E-4F78-BDF5-A606A8083BF9}图示
表示方法
注意点
适用范围
A
O
B
O
1
α
用三个大写字母表示:∠AOB 或∠BOA
顶点的字
母必须写在中间
所有角
用一个大写字母表示:∠O
用一个阿拉伯数字或希腊字母表示:∠1,∠ α
只适用于顶点处只有一个角
顶点处只有一个角
角的内部弧线加相应的数字或希腊字母
所有角
∠ABC<∠DEF
B
C
A
E
D
F
叠合法比较
DE边在∠ABC的外部,则
四、角的大小比较:1.度量法,2.叠合法
∠ABC=∠DEF
B
A
C
E
D
F
DE与AB边重合,则
叠合法比较
∠ABC>∠DEF
B
A
C
D
E
F
DE边在∠ABC的内部,则
叠合法比较
用叠合法比较角的大小,注意:
1.两角的顶点必须重合;
2.一边必须重合,另一边落在重 合的一边的同侧.
五、角平分线的定义
以一个角的顶点为端点的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线
O
A
B
C
4、写出图中
(1)能用一个字母表示的角 ( )
(2)以B为顶点的角( )
(3)图中共有几个角(小于平角的角)
( )
当堂训练:
1.如图所示,下列表示角的方法错误的是 ( )
A.∠1与∠AOB表示同一个角
B.∠β表示的是∠BOC
C.图中共有三个角:∠AOB,∠AOC,∠BOC
D.∠AOC也可用∠O来表示
D
2、如图, (1)能用一个字母表示的角有
( )
(2)以B为顶点的角有
( )
(3)图中共有几个角(小于平角的角)
( )
A
B
E
C
∠A 和∠C
(∠A 、∠C 、∠ABE 、∠EBC、 ∠ABC、 ∠AEB 、∠CEB)
∠ABE、∠EBC、 ∠ABC
7个角
3.下列说法不正确的是 ( )
A.角是有公共端点的两条射线组成的图形
B.周角大小是平角的2倍
C.平角就是一条直线,周角就是一条射线
D.周角的始边与终边重合
C
4.∠ABC与∠MNP相比较,若顶点B与N重合,且BC与MN重合,BA在∠MNP的内部,则它们的大小关系 ( )
A.∠ABC>∠MNP B.∠ABC=∠MNP
C.∠ABC<∠MNP D.不能确定
5.已知OC是∠AOB的平分线,下列结论不正确的是 ( )
C
A
6.已知OC平分∠AOB,∠AOB=64°,则∠AOC的度数是_________
7.如图,直线AB,CD相交于点O,OE平分∠AOD,若∠BOD=100°,则∠AOE=________.
32°
40°
拓展延伸:
8、如图,在锐角∠AOB内部,画1条射线,可得3个锐角;画2条不同射线,可得6个锐角;画3条不同射线,可得10个锐角;…;照此规律,画10条不同射线,可得锐角______个.
课堂小结:
本节课你有什么收获?
学习目标:
1.理解角的概念和角的表示方法
2.掌握角的大小比较的方法
3.掌握角平分线的定义
谢谢!
吊扇扇叶的夹角
剪刀的角
人仰视时的视角
楼梯的折角
时针和分针的夹角
角与角的大小比较
学习目标:
1.掌握角的概念和角的表示方法
2.掌握角的大小比较的方法
3.掌握角平分线的定义
问题导学(阅读教材P123-125,思考下列问题)
1.角的定义是什么?
2.什么是平角?什么是周角?
3.角有哪些表示方法?用这些方法表示角时要注意哪些地方?
4.如何比较两个角的大小?你有哪些方法?
5.角平分线是怎样定义的?
角是有公共端点的两条射线所组成的图形.
这个公共端点叫做这个角的顶点
这两条射线叫做这个角的边
一、角的概念
顶点
边
边
动态的观点
角也可以看成是一条射线绕着它的端点旋转而成的图形.
顶点
始边
起始位置的射线叫做这个角的始边
终边
终止位置的射线叫做这个角的终边
始边旋转到终边所扫过的区域,
叫角的内部
O
A
B
当射线绕着端点旋转到与原来的位置在同一直线上但方向相反时,所成的角叫做平角.
二、平角与周角
O
A
(B)
当射线绕着端点旋转一周,又回到原来的位置时,所成的角叫做周角.
三、角的表示方法
{C4B1156A-380E-4F78-BDF5-A606A8083BF9}图示
表示方法
注意点
适用范围
A
O
B
O
1
α
用三个大写字母表示:∠AOB 或∠BOA
顶点的字
母必须写在中间
所有角
用一个大写字母表示:∠O
用一个阿拉伯数字或希腊字母表示:∠1,∠ α
只适用于顶点处只有一个角
顶点处只有一个角
角的内部弧线加相应的数字或希腊字母
所有角
∠ABC<∠DEF
B
C
A
E
D
F
叠合法比较
DE边在∠ABC的外部,则
四、角的大小比较:1.度量法,2.叠合法
∠ABC=∠DEF
B
A
C
E
D
F
DE与AB边重合,则
叠合法比较
∠ABC>∠DEF
B
A
C
D
E
F
DE边在∠ABC的内部,则
叠合法比较
用叠合法比较角的大小,注意:
1.两角的顶点必须重合;
2.一边必须重合,另一边落在重 合的一边的同侧.
五、角平分线的定义
以一个角的顶点为端点的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线
O
A
B
C
4、写出图中
(1)能用一个字母表示的角 ( )
(2)以B为顶点的角( )
(3)图中共有几个角(小于平角的角)
( )
当堂训练:
1.如图所示,下列表示角的方法错误的是 ( )
A.∠1与∠AOB表示同一个角
B.∠β表示的是∠BOC
C.图中共有三个角:∠AOB,∠AOC,∠BOC
D.∠AOC也可用∠O来表示
D
2、如图, (1)能用一个字母表示的角有
( )
(2)以B为顶点的角有
( )
(3)图中共有几个角(小于平角的角)
( )
A
B
E
C
∠A 和∠C
(∠A 、∠C 、∠ABE 、∠EBC、 ∠ABC、 ∠AEB 、∠CEB)
∠ABE、∠EBC、 ∠ABC
7个角
3.下列说法不正确的是 ( )
A.角是有公共端点的两条射线组成的图形
B.周角大小是平角的2倍
C.平角就是一条直线,周角就是一条射线
D.周角的始边与终边重合
C
4.∠ABC与∠MNP相比较,若顶点B与N重合,且BC与MN重合,BA在∠MNP的内部,则它们的大小关系 ( )
A.∠ABC>∠MNP B.∠ABC=∠MNP
C.∠ABC<∠MNP D.不能确定
5.已知OC是∠AOB的平分线,下列结论不正确的是 ( )
C
A
6.已知OC平分∠AOB,∠AOB=64°,则∠AOC的度数是_________
7.如图,直线AB,CD相交于点O,OE平分∠AOD,若∠BOD=100°,则∠AOE=________.
32°
40°
拓展延伸:
8、如图,在锐角∠AOB内部,画1条射线,可得3个锐角;画2条不同射线,可得6个锐角;画3条不同射线,可得10个锐角;…;照此规律,画10条不同射线,可得锐角______个.
课堂小结:
本节课你有什么收获?
学习目标:
1.理解角的概念和角的表示方法
2.掌握角的大小比较的方法
3.掌握角平分线的定义
谢谢!
同课章节目录
