2.2.2《整式的加减(去括号)》课件-(人教版七年级上数学)(共16张PPT)
文档属性
| 名称 | 2.2.2《整式的加减(去括号)》课件-(人教版七年级上数学)(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 479.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 00:00:00 | ||
图片预览

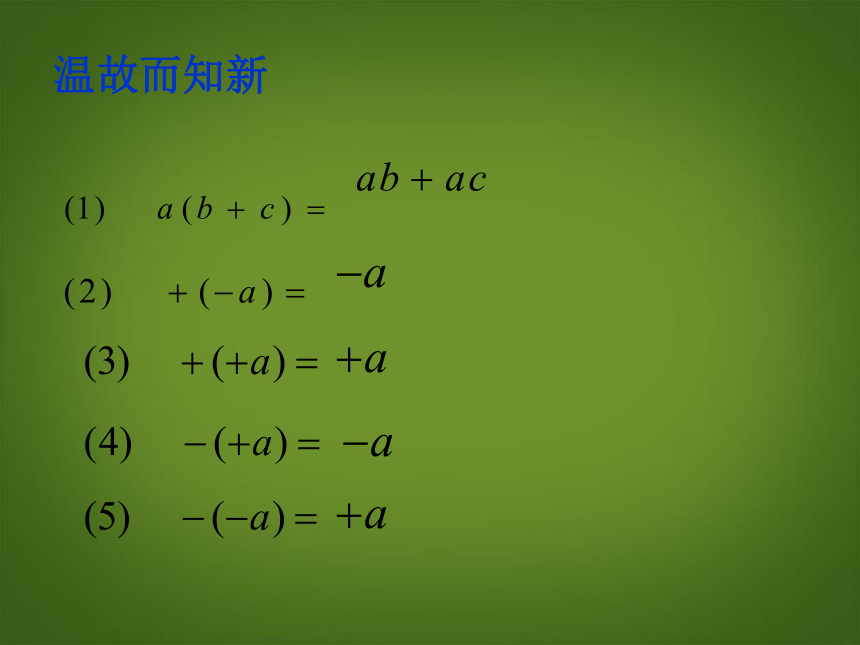

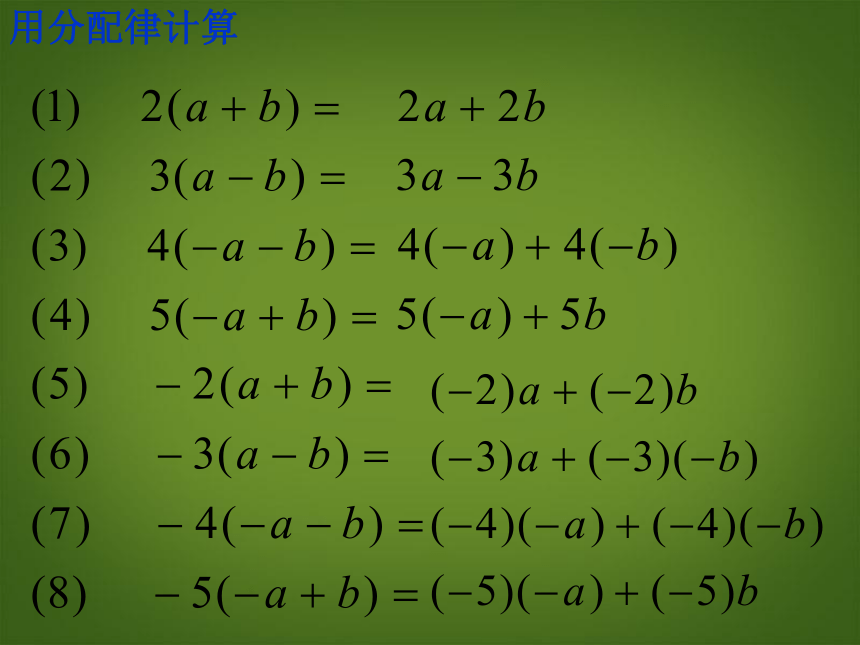

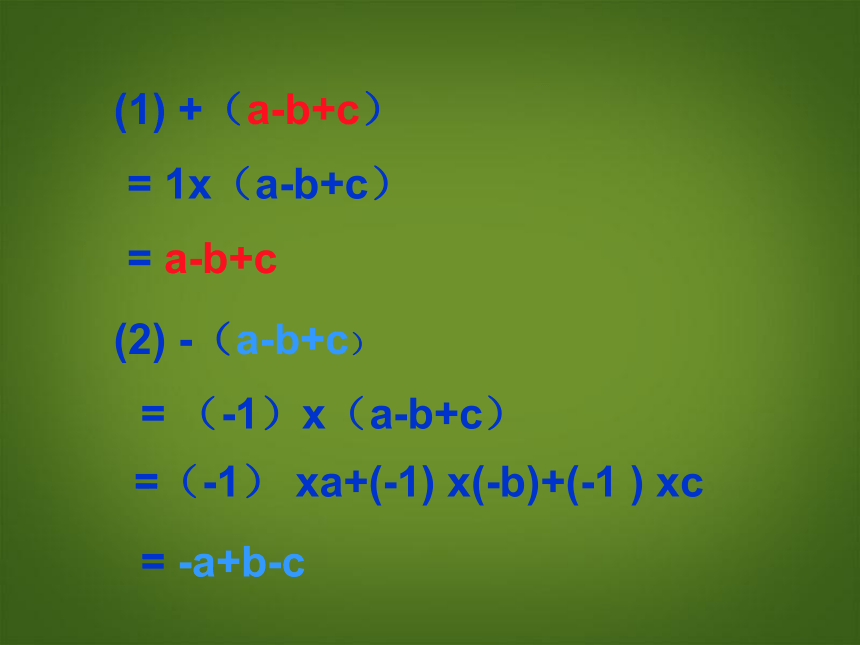

文档简介
去括号
温故而知新
=(-1)x(3-7)
复习旧知
-(+5)=
+(+5)=
-(-7)=
+(-7)=
- 5
+5
+7
-7
1. 化简
=(-1) x 3+(-1) x(-7)
= - 3 + 7
= 1 x 3+1 x (-7)
= 3 - 7
2. 去括号
① -(3- 7)
② +(3- 7)
+3 与-7的 和
=(+1) x(3-7)
观察这两组算式,看看去括号前后,括号里各项的符号有什么变化?
用分配律计算
想一想
根据分配律,你能为下面的式子去括号吗?
(1) +(a-b)
(2) -(a-b)
= 1x(a-b)
= (-1)x(a-b)
观察这两组算式,看看去括号前后,括号里各项的符号有什么变化?
= a-b
= -a+b
=(-1) xa+(-1) x(-b)
(1) +(a-b+c)
(2) -(a-b+c)
= 1x(a-b+c)
= (-1)x(a-b+c)
= a-b+c
= -a+b-c
=(-1) xa+(-1) x(-b)+(-1 ) xc
如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同.
如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
顺口溜:
去括号,看符号:
是“+”号,不变号;
是“-”号,全变号;
原来的符号和括号都扔掉.
练习:
(1)去括号:
a+(b-c)=
————
a+(- b+c)=
————
a- (b-c)=
————
a- (- b+c)=
————
(2)判断正误
a-(b+c)=a-b+c ( )
a-(b-c)=a-b-c ( )
2b+(-3a+1)=2b-3a-1 ( )
3a-(3b-c)=3a-3b+c ( )
×
×
×
a+b-c
a-b+c
a-b+c
a+b-c
a-b-c
a-b+c
2b-3a+1
√
例:为下面的式子去括号
= +(3a-3b+3c)
= 3a-3b+3c
= -3a+3b-3c
= -(3a-3b+3c)
= +[3(a-b+c)]
= -[3(a-b+c)]
(1) +3(a - b+c) (2)- 3(a - b+c)
结论:括号外面的因数不是1或-1时,把符号留在外面,把因数的绝对值按分配率乘进去,最后再去括号.
练习1:去括号
① 9(x-z)
②-3(-b+c)
③4(-a+b-c)
④-7(-x-y+z)
= 9x+9×(-z)
= 9x- 9z
=-[3×(-b)+3c]
=-(-3b+3c)
=3b-3c
= 4×(-a)+4b+4×(-c)
= - 4a+4b- 4c
= - [7(-x)+7(-y)+7z]
= - (-7x-7y+7z)
= 7x+7y-7z
(1)去括号时应先判断括号前面是“+”号还是“-”号。
(2)去括号后,括号内各项符号要么全变号,
要么全不变。
(3)括号前面是“-”号时,去掉括号后,括号内
的各项符号都要变成相反,不能只改变第一
项或前几项的符号。
(4)括号内原有几项,去掉括号后仍有几项,
不能丢项。
(5)去括号法则的依据是分配律,计算时
不能出现有些项漏乘的情况。
典型例题
化简下列各式
例题2
两船从同一港口同时出发反向而行,甲船顺水,乙船逆水,两船在静水中的速度都是50 km/h,水流速度是a km/h.
(1)2h后两船相距多远?
(2) 2h后甲船比乙船多航行多少千米?
① 2(3a+b)
③ -3(-2a+3b)
②-7(-a+3b-2c)
④ 4(2x-3y+3c)
练习2:去括号
=2 ×3a+2b
=6a+2b
= - [ 7(-a)+7 ×3b+7 ×(-2c)
= - (-7a+21b-14)
= 7a-21b+14c
=-[3 ×(-2a)+3×3b]
=-(-6a+9b)
=6a-9b
=4 ×2x+4×(-3y)+4×3c
=8x-12y+12c
行家看门道
火眼金睛
判断下列各题中的正误:
×
×
×
×
√
1、4a+(-a+3)=4a+a+3=5a+3
2、 (2a-b)-(6b-7a)=2a-b-6b-7a=-5a-7b
3、3(x-2y)-2(4x-6y)=3x-6y-8x+6y=-5x
4、-(2x+4y)+(6x-2y+1)=-2x-4y+6x-2y=4x-6y
5、4-3(2x-5)=4-6x+15=19-6x
下课了!
2. 课本69页 习题2.2 第2题
作业:
温故而知新
=(-1)x(3-7)
复习旧知
-(+5)=
+(+5)=
-(-7)=
+(-7)=
- 5
+5
+7
-7
1. 化简
=(-1) x 3+(-1) x(-7)
= - 3 + 7
= 1 x 3+1 x (-7)
= 3 - 7
2. 去括号
① -(3- 7)
② +(3- 7)
+3 与-7的 和
=(+1) x(3-7)
观察这两组算式,看看去括号前后,括号里各项的符号有什么变化?
用分配律计算
想一想
根据分配律,你能为下面的式子去括号吗?
(1) +(a-b)
(2) -(a-b)
= 1x(a-b)
= (-1)x(a-b)
观察这两组算式,看看去括号前后,括号里各项的符号有什么变化?
= a-b
= -a+b
=(-1) xa+(-1) x(-b)
(1) +(a-b+c)
(2) -(a-b+c)
= 1x(a-b+c)
= (-1)x(a-b+c)
= a-b+c
= -a+b-c
=(-1) xa+(-1) x(-b)+(-1 ) xc
如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同.
如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
顺口溜:
去括号,看符号:
是“+”号,不变号;
是“-”号,全变号;
原来的符号和括号都扔掉.
练习:
(1)去括号:
a+(b-c)=
————
a+(- b+c)=
————
a- (b-c)=
————
a- (- b+c)=
————
(2)判断正误
a-(b+c)=a-b+c ( )
a-(b-c)=a-b-c ( )
2b+(-3a+1)=2b-3a-1 ( )
3a-(3b-c)=3a-3b+c ( )
×
×
×
a+b-c
a-b+c
a-b+c
a+b-c
a-b-c
a-b+c
2b-3a+1
√
例:为下面的式子去括号
= +(3a-3b+3c)
= 3a-3b+3c
= -3a+3b-3c
= -(3a-3b+3c)
= +[3(a-b+c)]
= -[3(a-b+c)]
(1) +3(a - b+c) (2)- 3(a - b+c)
结论:括号外面的因数不是1或-1时,把符号留在外面,把因数的绝对值按分配率乘进去,最后再去括号.
练习1:去括号
① 9(x-z)
②-3(-b+c)
③4(-a+b-c)
④-7(-x-y+z)
= 9x+9×(-z)
= 9x- 9z
=-[3×(-b)+3c]
=-(-3b+3c)
=3b-3c
= 4×(-a)+4b+4×(-c)
= - 4a+4b- 4c
= - [7(-x)+7(-y)+7z]
= - (-7x-7y+7z)
= 7x+7y-7z
(1)去括号时应先判断括号前面是“+”号还是“-”号。
(2)去括号后,括号内各项符号要么全变号,
要么全不变。
(3)括号前面是“-”号时,去掉括号后,括号内
的各项符号都要变成相反,不能只改变第一
项或前几项的符号。
(4)括号内原有几项,去掉括号后仍有几项,
不能丢项。
(5)去括号法则的依据是分配律,计算时
不能出现有些项漏乘的情况。
典型例题
化简下列各式
例题2
两船从同一港口同时出发反向而行,甲船顺水,乙船逆水,两船在静水中的速度都是50 km/h,水流速度是a km/h.
(1)2h后两船相距多远?
(2) 2h后甲船比乙船多航行多少千米?
① 2(3a+b)
③ -3(-2a+3b)
②-7(-a+3b-2c)
④ 4(2x-3y+3c)
练习2:去括号
=2 ×3a+2b
=6a+2b
= - [ 7(-a)+7 ×3b+7 ×(-2c)
= - (-7a+21b-14)
= 7a-21b+14c
=-[3 ×(-2a)+3×3b]
=-(-6a+9b)
=6a-9b
=4 ×2x+4×(-3y)+4×3c
=8x-12y+12c
行家看门道
火眼金睛
判断下列各题中的正误:
×
×
×
×
√
1、4a+(-a+3)=4a+a+3=5a+3
2、 (2a-b)-(6b-7a)=2a-b-6b-7a=-5a-7b
3、3(x-2y)-2(4x-6y)=3x-6y-8x+6y=-5x
4、-(2x+4y)+(6x-2y+1)=-2x-4y+6x-2y=4x-6y
5、4-3(2x-5)=4-6x+15=19-6x
下课了!
2. 课本69页 习题2.2 第2题
作业:
