六年级数学下册课件-6.2.1 《 图形的认识与测量》人教版(共30张PPT)
文档属性
| 名称 | 六年级数学下册课件-6.2.1 《 图形的认识与测量》人教版(共30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 00:00:00 | ||
图片预览








文档简介
(共30张PPT)
图形的认识与测量
(一)线
1.特征
图示
名称
特
点
直线
没有端点,无限长,无法度量长度
射线
有一个端点,无限长,无法度量长度
线段
有两个端点,可以度量长度
垂线
在同一平面内,两条直线相交成直角
(画垂线的方法)
平行线
在同一平面内,不相交的两条直线
(画平行线的方法)
过一点可以画出无数条射线。
过一点可以画出无数直线。
过两点可以画出一条直线。
点到直线的距离
从直线外一点到这条直线所画的垂直线段的长度,叫做这个点到直线的距离。
过一点可以画出无数条射线。
过一点可以画出无数直线。
过两点可以画出一条直线。
同一平面内的两条直线不知平行,就是相交,垂直是相交的特例。
轻松一练
数一数,下图中有(
)条直线,(
)条射线,(
)条线段
A
B
C
D
1
8
6
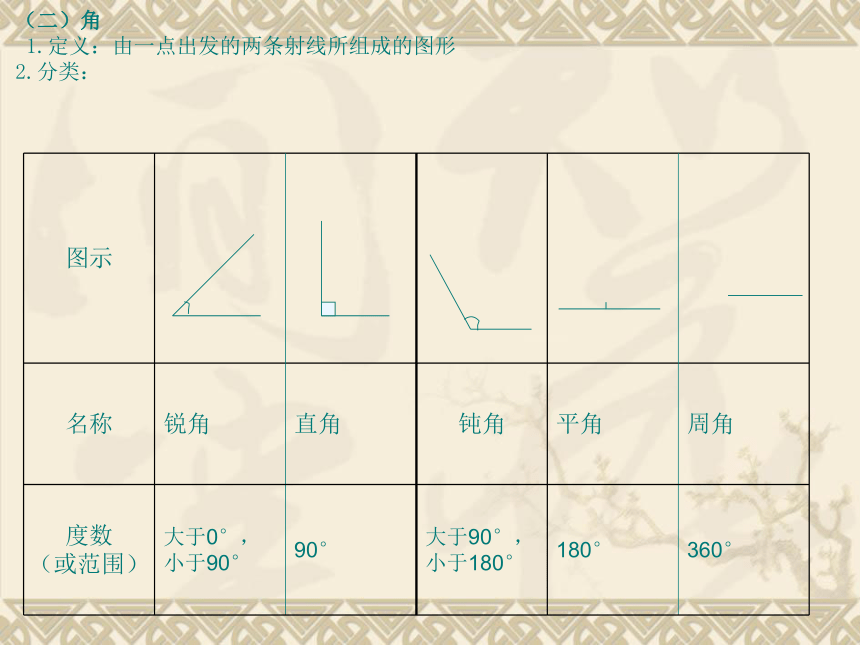
(二)角
1.定义:由一点出发的两条射线所组成的图形
2.分类:
图示
名称
锐角
直角
钝角
平角
周角
度数
(或范围)
大于0°,小于90°
90°
大于90°,小于180°
180°
360°
平面图形
(一)三角形和四边形
1.三角形
定义
由不在同一条直线上的三条线段着尾顺次相接围成的图形叫三角形。
分类
按角分
锐角三角形
三个角都是锐角
三个角都小于90°
直角三角形
有一个角是直角
有一个角等于90°
钝角三角形
有一个角是钝角
有一个角大于90°
按边分
等腰三角形
两条边相等
等边三角形
三条边全相等
每个内角都是60°
不等边三角形
三条边都不相等
图形及字母意义
面积公式
特征
三角形
a——底
h——高
S=ah÷2
面积=底?高÷2
?两边之和大于第三条边。
?两边之差小于第三条边。
?三个角的内角和是180°。
?有三条边和三个角,具有稳定性。
2.四边形
定义
由不在同一直线上的四条线段首尾顺次相接围成的封闭图形叫四边形
分类
平行四边形
平行四边形
两组对边分别平行且相等
长方形
两对边分别相等
四个角都是直角
正方形
四条边都相等
四个角都是直角
梯形
一般梯形
只有一组对边平行,两腰不等长的梯形。
等腰梯形
只有一组对边平行,两条腰相等的梯形。
直角梯形
一条腰与底垂直的梯形叫做直角梯形。
有两个角是直角
图形及字母意义
面积公式
特征
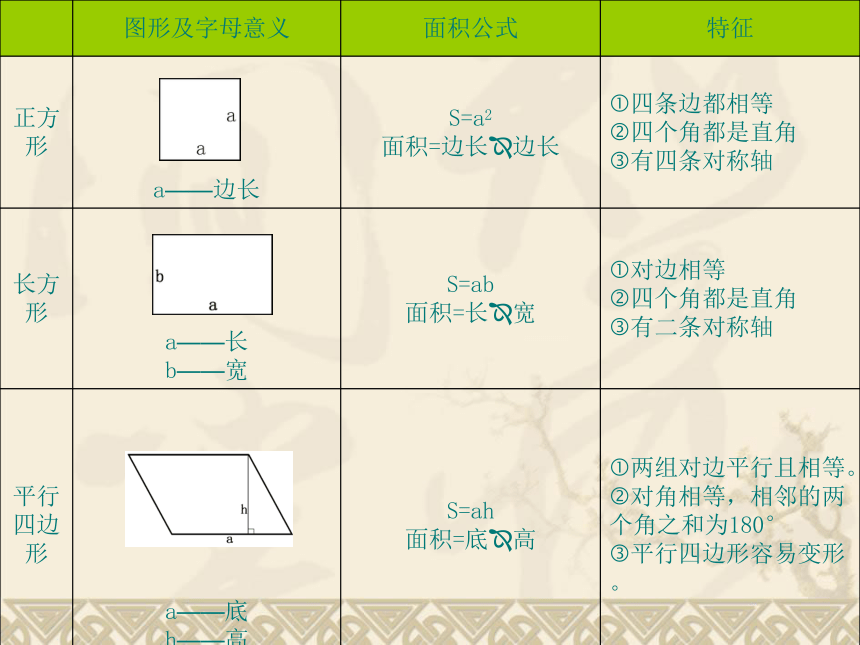
正方形
a——边长
S=a2
面积=边长?边长
?四条边都相等
?四个角都是直角
?有四条对称轴
长方形
a——长
b——宽
S=ab
面积=长?宽
?对边相等
?四个角都是直角
?有二条对称轴
平行
四边形
a——底
h——高
S=ah
面积=底?高
?两组对边平行且相等。
?对角相等,相邻的两个角之和为180°
?平行四边形容易变形。
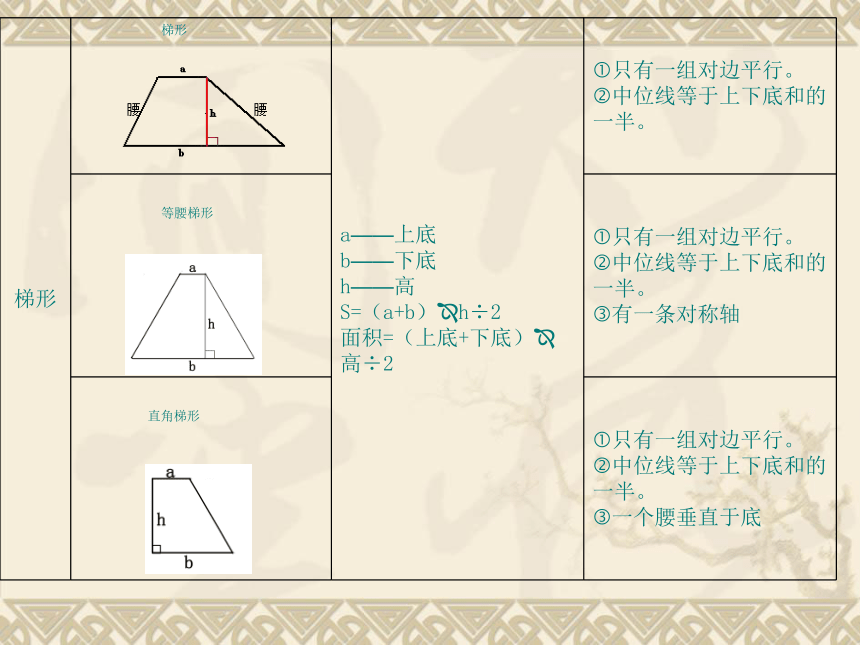
梯形
等腰梯形
直角梯形
梯形
a——上底
b——下底
h——高
S=(a+b)?h÷2
面积=(上底+下底)?高÷2
?只有一组对边平行。
?中位线等于上下底和的一半。
?只有一组对边平行。
?中位线等于上下底和的一半。
?有一条对称轴
?只有一组对边平行。
?中位线等于上下底和的一半。
?一个腰垂直于底
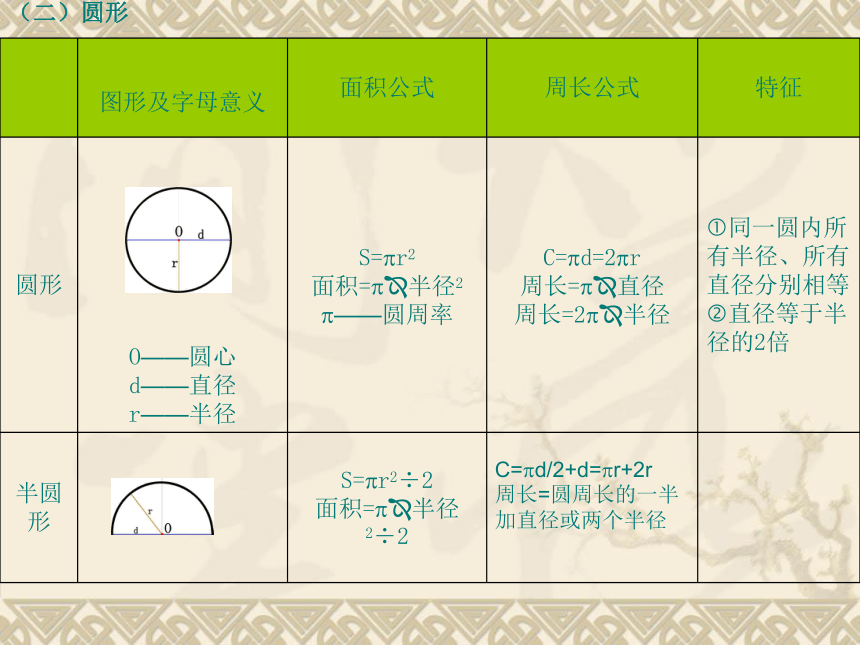
(二)圆形
图形及字母意义
面积公式
周长公式
特征
圆形
O——圆心
d——直径
r——半径
S=?r2
面积=??半径2
?——圆周率
C=?d=2?r
周长=??直径
周长=2??半径
?同一圆内所有半径、所有直径分别相等
?直径等于半径的2倍
半圆形
S=?r2÷2
面积=??半径2÷2
C=?d/2+d=?r+2r
周长=圆周长的一半加直径或两个半径
一、填空
用圆规画一个周长是25.12
cm的圆,圆规两脚间的距离
是(
)
cm
,这个圆的面积是(
)cm2。
2.一个平行四边形的底是5
dm,面积是12dm2,高是(
)dm,
与它等底等高的三角形面积是(
)
dm2
。
3.一个三角形的底是6cm,面积是24cm2,高是(
)cm。
4.如下图,梯形的面积是(
)cm2;如果在梯形中剪下一个最大的三角形,这个三角形的面积是(
)
cm2。
4
50.24
2.4
6
8
144
96
5.用两个边长5cm的正方形拼成一个长方形,这个长方形
的周长是(
)cm,面积是(
)cm2。
6.长方形的周长是30厘米,长与宽的比为3:2,这个长方形的
长是(
)厘米,面积是(
)平方厘米。
7.正方形的边长扩大5倍,它的周长扩大(
)倍,面积扩大
(
)倍。
8.一个三角形与一个平行四边形的面积相等,底也相等,那么
当三角形高是8厘米时,平行四边形的高是(
)厘米。
9.在边长为12厘米的正方形中剪一个最大的圆,剩下图形的周长
是(
)厘米。剩下图形的面积是(
)平方厘米。
10.求半圆的周长就是求(
)与(
)的和。
求半圆的面积就是求(
)。
30
50
9
54
5
25
4
85.68
30.96
圆周长的一半
直径
圆面积的一半
二、判断
1.一个圆的半径是2厘米,它的周长与面积相等。
2.平行四边形的面积是三角形的2倍。
3.两个半圆可以合成一个圆。
4.一个长方形,长增加5厘米,宽增加4厘米,它的
面积就增加20平方厘米。
5.面积相等的正方形,周长相等,所以面积相等的长方形
周长也相等。
×
×
×
×
×
三、计算下列各平面图形的周长与面积
(单位:cm)
30
12
①
30
12
②
比一比,①号图与②号图的周长与面积的异同?
立体图形
(一)正方体和长方体
图形及字母意义
特征
侧面积
表面积
体积
正方体、立方体
a——边长
6个面的
12条棱
8个顶点
6个面完全相等
S侧=Ch
侧面积=
底面周长?高
S表=6a2
V=
S表?h
V=
a
a
a
长方体
a——长
b——宽
h——高
相对的两个面完全相等
S表=(ab+ah+bh)?2
V=abh
正方体展开图
长方体展开图
图形及字母意义
特征
表面积
体积
h——高
r——底面积的半径
S——底面积
?上、下底面是相等的两个圆形。
?两个底之间的距离叫做高(h)?侧面展开是个长方形或正方形。
?这个长方形或正方形的长相当于圆柱体底面周长。
?这个长方形或正方形的宽相当于圆柱体的高。
?圆柱体有无数条高。
S侧=Ch=2?rh
S表=
S侧+2S底
=
Ch+2?r2
V=
S底h=?r2h
h——高
r——底面积的半径
S——底面积
?只有一个顶点
?底面是一个圆,侧面展开是一个扇形。
?顶点到圆心的距离叫做高(h)?圆锥体有且只有一个高。
V=S底h
=?r2h
(二)圆柱和圆锥
圆柱体展开图
圆锥体展开图
一、填空:
1、用一根24
厘米长的铁丝焊成一个最大的立方体模型,它的表面积是(
),体积是(
)。
2、一个底面是正方形的长方体,底面周长是20
厘米,高是12
厘米,它的表面积是(
),体积是(
)
3、一个圆柱的底面直径和高都是10
厘米,它的侧面积是(
),表面积是(
),体积(
)。
4、一段圆柱形木头,把它制成一个最大的圆锥体,削去部分
的体积是圆柱体积的(
),是圆锥体积的(
)。
判断题:
1、圆柱体的体积等于圆锥体的3倍。(
)
2、一个正方体的棱长是6厘米,它的表面积和体积相等。(
)
3、
容器的容积与容器的体积大小不一样
。(
)
造一个长40米,宽25米,深3米的游泳池。
(1)要挖出多少立方米土?
(2)沿着游泳池的周围走一圈,至少有多少米?
(3)如果在池的四壁和底面贴边长是2分米的方形瓷砖,那么需要多少块这样的瓷砖?
图形变换与位置
(一)图形的变换
1.轴对称图形
定义
如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形就是轴对称图形。
折痕所在的直线是轴对称图形的对称轴。
特征
?轴对称图形沿着对称轴对折后,两侧能够完全重合,两侧对称的点完全重合,对称的线段完全重合。
?对称点到对称轴之间的距离相等。
2.图形变换
(1)对称:?找准对应点的位置
?无坐标时,根据对应点到对称轴间的距离相等。
(2)平移与旋转:
意义
特点
平移
物体或图形沿着直线运动的现象。
做直线运动
旋转
物体绕着一个点或一个轴运动的现象。
做圆周运动
?对应点的平移
?对应点的旋转
(3)缩放:
对应线段同时缩小或扩大。
(二)图形与位置
(1)比例尺及坐标方位:
?比例尺:一般以1厘米的距离相当于实际距离多少
(2)根据方向、距离确定位置:
?首先确定方向
?根据比例尺确定直线距离
(3)路线描述:
?坐标原点——参照物
?目标相对于参照物方向
?目标到参照物的距离。
(4)用数字标注位置:
?坐标原点——参照物
?目标相对于参照物方向
?目标相对于参照物的角度
?目标到参照物的距离。
图形
名称
等腰
三角形
等腰
梯形
长方形
等边
三角形
正方形
圆
环形
对称轴
条数
1、等腰三角形、梯形和圆都是轴对称图形。(
)
2、所有的直径都是圆的对称轴。(
)
3、平行四边形也可能是轴对称图形。(
)
4、圆的直径是半径的2倍。(
)
5、通过一个圆的圆心的直线是这个圆的对称轴。
( )
6、圆是轴对称图形,每一条直径都是它的对称轴。( )
7、等腰梯形是对称图形。
(
)
8、正方形只有一条对称轴。
(
)
填一填。
如果一个图形沿着一条直线对折,两侧的图形能
够完全重合,这样的图形就叫(
)图形,
那条直线就是(
)。
正方形有(
)条对称轴。
这些现象哪些是“平移”现象,哪些是“旋转”现象:
(1)张叔叔在笔直的公路上开车,方向盘的运动
(2)升国旗时,国旗的升降运动。
(3)妈妈用拖布擦地。
(4)自行车的车轮转了一圈又一圈。
(1)从角上拿一个,它的体积表面积是怎样变化的?
(2)现在它的体积和表面积发生怎样的变化?
(3)从中间拿掉一个,它的体积和表面积发生怎样的变化?
图形的认识与测量
(一)线
1.特征
图示
名称
特
点
直线
没有端点,无限长,无法度量长度
射线
有一个端点,无限长,无法度量长度
线段
有两个端点,可以度量长度
垂线
在同一平面内,两条直线相交成直角
(画垂线的方法)
平行线
在同一平面内,不相交的两条直线
(画平行线的方法)
过一点可以画出无数条射线。
过一点可以画出无数直线。
过两点可以画出一条直线。
点到直线的距离
从直线外一点到这条直线所画的垂直线段的长度,叫做这个点到直线的距离。
过一点可以画出无数条射线。
过一点可以画出无数直线。
过两点可以画出一条直线。
同一平面内的两条直线不知平行,就是相交,垂直是相交的特例。
轻松一练
数一数,下图中有(
)条直线,(
)条射线,(
)条线段
A
B
C
D
1
8
6
(二)角
1.定义:由一点出发的两条射线所组成的图形
2.分类:
图示
名称
锐角
直角
钝角
平角
周角
度数
(或范围)
大于0°,小于90°
90°
大于90°,小于180°
180°
360°
平面图形
(一)三角形和四边形
1.三角形
定义
由不在同一条直线上的三条线段着尾顺次相接围成的图形叫三角形。
分类
按角分
锐角三角形
三个角都是锐角
三个角都小于90°
直角三角形
有一个角是直角
有一个角等于90°
钝角三角形
有一个角是钝角
有一个角大于90°
按边分
等腰三角形
两条边相等
等边三角形
三条边全相等
每个内角都是60°
不等边三角形
三条边都不相等
图形及字母意义
面积公式
特征
三角形
a——底
h——高
S=ah÷2
面积=底?高÷2
?两边之和大于第三条边。
?两边之差小于第三条边。
?三个角的内角和是180°。
?有三条边和三个角,具有稳定性。
2.四边形
定义
由不在同一直线上的四条线段首尾顺次相接围成的封闭图形叫四边形
分类
平行四边形
平行四边形
两组对边分别平行且相等
长方形
两对边分别相等
四个角都是直角
正方形
四条边都相等
四个角都是直角
梯形
一般梯形
只有一组对边平行,两腰不等长的梯形。
等腰梯形
只有一组对边平行,两条腰相等的梯形。
直角梯形
一条腰与底垂直的梯形叫做直角梯形。
有两个角是直角
图形及字母意义
面积公式
特征
正方形
a——边长
S=a2
面积=边长?边长
?四条边都相等
?四个角都是直角
?有四条对称轴
长方形
a——长
b——宽
S=ab
面积=长?宽
?对边相等
?四个角都是直角
?有二条对称轴
平行
四边形
a——底
h——高
S=ah
面积=底?高
?两组对边平行且相等。
?对角相等,相邻的两个角之和为180°
?平行四边形容易变形。
梯形
等腰梯形
直角梯形
梯形
a——上底
b——下底
h——高
S=(a+b)?h÷2
面积=(上底+下底)?高÷2
?只有一组对边平行。
?中位线等于上下底和的一半。
?只有一组对边平行。
?中位线等于上下底和的一半。
?有一条对称轴
?只有一组对边平行。
?中位线等于上下底和的一半。
?一个腰垂直于底
(二)圆形
图形及字母意义
面积公式
周长公式
特征
圆形
O——圆心
d——直径
r——半径
S=?r2
面积=??半径2
?——圆周率
C=?d=2?r
周长=??直径
周长=2??半径
?同一圆内所有半径、所有直径分别相等
?直径等于半径的2倍
半圆形
S=?r2÷2
面积=??半径2÷2
C=?d/2+d=?r+2r
周长=圆周长的一半加直径或两个半径
一、填空
用圆规画一个周长是25.12
cm的圆,圆规两脚间的距离
是(
)
cm
,这个圆的面积是(
)cm2。
2.一个平行四边形的底是5
dm,面积是12dm2,高是(
)dm,
与它等底等高的三角形面积是(
)
dm2
。
3.一个三角形的底是6cm,面积是24cm2,高是(
)cm。
4.如下图,梯形的面积是(
)cm2;如果在梯形中剪下一个最大的三角形,这个三角形的面积是(
)
cm2。
4
50.24
2.4
6
8
144
96
5.用两个边长5cm的正方形拼成一个长方形,这个长方形
的周长是(
)cm,面积是(
)cm2。
6.长方形的周长是30厘米,长与宽的比为3:2,这个长方形的
长是(
)厘米,面积是(
)平方厘米。
7.正方形的边长扩大5倍,它的周长扩大(
)倍,面积扩大
(
)倍。
8.一个三角形与一个平行四边形的面积相等,底也相等,那么
当三角形高是8厘米时,平行四边形的高是(
)厘米。
9.在边长为12厘米的正方形中剪一个最大的圆,剩下图形的周长
是(
)厘米。剩下图形的面积是(
)平方厘米。
10.求半圆的周长就是求(
)与(
)的和。
求半圆的面积就是求(
)。
30
50
9
54
5
25
4
85.68
30.96
圆周长的一半
直径
圆面积的一半
二、判断
1.一个圆的半径是2厘米,它的周长与面积相等。
2.平行四边形的面积是三角形的2倍。
3.两个半圆可以合成一个圆。
4.一个长方形,长增加5厘米,宽增加4厘米,它的
面积就增加20平方厘米。
5.面积相等的正方形,周长相等,所以面积相等的长方形
周长也相等。
×
×
×
×
×
三、计算下列各平面图形的周长与面积
(单位:cm)
30
12
①
30
12
②
比一比,①号图与②号图的周长与面积的异同?
立体图形
(一)正方体和长方体
图形及字母意义
特征
侧面积
表面积
体积
正方体、立方体
a——边长
6个面的
12条棱
8个顶点
6个面完全相等
S侧=Ch
侧面积=
底面周长?高
S表=6a2
V=
S表?h
V=
a
a
a
长方体
a——长
b——宽
h——高
相对的两个面完全相等
S表=(ab+ah+bh)?2
V=abh
正方体展开图
长方体展开图
图形及字母意义
特征
表面积
体积
h——高
r——底面积的半径
S——底面积
?上、下底面是相等的两个圆形。
?两个底之间的距离叫做高(h)?侧面展开是个长方形或正方形。
?这个长方形或正方形的长相当于圆柱体底面周长。
?这个长方形或正方形的宽相当于圆柱体的高。
?圆柱体有无数条高。
S侧=Ch=2?rh
S表=
S侧+2S底
=
Ch+2?r2
V=
S底h=?r2h
h——高
r——底面积的半径
S——底面积
?只有一个顶点
?底面是一个圆,侧面展开是一个扇形。
?顶点到圆心的距离叫做高(h)?圆锥体有且只有一个高。
V=S底h
=?r2h
(二)圆柱和圆锥
圆柱体展开图
圆锥体展开图
一、填空:
1、用一根24
厘米长的铁丝焊成一个最大的立方体模型,它的表面积是(
),体积是(
)。
2、一个底面是正方形的长方体,底面周长是20
厘米,高是12
厘米,它的表面积是(
),体积是(
)
3、一个圆柱的底面直径和高都是10
厘米,它的侧面积是(
),表面积是(
),体积(
)。
4、一段圆柱形木头,把它制成一个最大的圆锥体,削去部分
的体积是圆柱体积的(
),是圆锥体积的(
)。
判断题:
1、圆柱体的体积等于圆锥体的3倍。(
)
2、一个正方体的棱长是6厘米,它的表面积和体积相等。(
)
3、
容器的容积与容器的体积大小不一样
。(
)
造一个长40米,宽25米,深3米的游泳池。
(1)要挖出多少立方米土?
(2)沿着游泳池的周围走一圈,至少有多少米?
(3)如果在池的四壁和底面贴边长是2分米的方形瓷砖,那么需要多少块这样的瓷砖?
图形变换与位置
(一)图形的变换
1.轴对称图形
定义
如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形就是轴对称图形。
折痕所在的直线是轴对称图形的对称轴。
特征
?轴对称图形沿着对称轴对折后,两侧能够完全重合,两侧对称的点完全重合,对称的线段完全重合。
?对称点到对称轴之间的距离相等。
2.图形变换
(1)对称:?找准对应点的位置
?无坐标时,根据对应点到对称轴间的距离相等。
(2)平移与旋转:
意义
特点
平移
物体或图形沿着直线运动的现象。
做直线运动
旋转
物体绕着一个点或一个轴运动的现象。
做圆周运动
?对应点的平移
?对应点的旋转
(3)缩放:
对应线段同时缩小或扩大。
(二)图形与位置
(1)比例尺及坐标方位:
?比例尺:一般以1厘米的距离相当于实际距离多少
(2)根据方向、距离确定位置:
?首先确定方向
?根据比例尺确定直线距离
(3)路线描述:
?坐标原点——参照物
?目标相对于参照物方向
?目标到参照物的距离。
(4)用数字标注位置:
?坐标原点——参照物
?目标相对于参照物方向
?目标相对于参照物的角度
?目标到参照物的距离。
图形
名称
等腰
三角形
等腰
梯形
长方形
等边
三角形
正方形
圆
环形
对称轴
条数
1、等腰三角形、梯形和圆都是轴对称图形。(
)
2、所有的直径都是圆的对称轴。(
)
3、平行四边形也可能是轴对称图形。(
)
4、圆的直径是半径的2倍。(
)
5、通过一个圆的圆心的直线是这个圆的对称轴。
( )
6、圆是轴对称图形,每一条直径都是它的对称轴。( )
7、等腰梯形是对称图形。
(
)
8、正方形只有一条对称轴。
(
)
填一填。
如果一个图形沿着一条直线对折,两侧的图形能
够完全重合,这样的图形就叫(
)图形,
那条直线就是(
)。
正方形有(
)条对称轴。
这些现象哪些是“平移”现象,哪些是“旋转”现象:
(1)张叔叔在笔直的公路上开车,方向盘的运动
(2)升国旗时,国旗的升降运动。
(3)妈妈用拖布擦地。
(4)自行车的车轮转了一圈又一圈。
(1)从角上拿一个,它的体积表面积是怎样变化的?
(2)现在它的体积和表面积发生怎样的变化?
(3)从中间拿掉一个,它的体积和表面积发生怎样的变化?
