北师大版八年级下册数学 2.5 一元一次不等式与一次函数课件(共24张ppt)
文档属性
| 名称 | 北师大版八年级下册数学 2.5 一元一次不等式与一次函数课件(共24张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 888.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 00:00:00 | ||
图片预览





文档简介
2.5
一元一次不等式与一次函数
提出问题
创设情境
我们来看下面的问题
2.
当自变量x为何值时函数y=2x-4值大于0?
这两个问题有什么关系?
这两个问题实际是同一个问题
1.解不等式:5x+6>3x+10
归纳
由于任何一元一次不等式都可以转化为ax+b
>0或ax+b<0(a,b为常数,a≠0)的形式,所以解一元一次不等式可以看作:当一次函数值大于或小于0时,求自变量相应的取值范围
导入新课
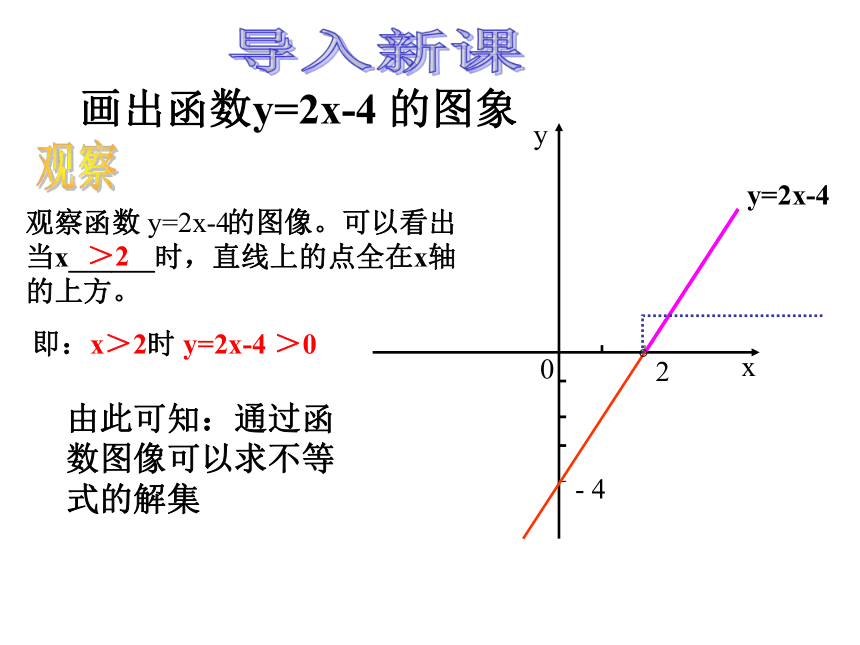
观察
观察函数
的图像。可以看出当x______时,直线上的点全在x轴的上方。
y=2x-4
即:x>2时
y=2x-4
>0
由此可知:通过函数图像可以求不等式的解集
画出函数y=2x-4
的图象
y=2x-4
2
-
4
x
y
0
>2
归纳
任何一元一次不等式都可以转化为ax+b
>0或ax+b<0(a,b为常数,a≠0)的形式。
解一元一次不等式可以:
从数的角度看,就是求一次函数y=
ax+b的值大于或小于0时相应的自变量的取值范围;
从形的角度看,就是确定直线y=ax+b在x轴上(或下)方部分所有的点的横坐标所构成的集合。
y
x
-2
y=3x+6
O
1.根据下列一次函数的图象,你能求出哪些不等式解集?并直接写出相应不等式的解集?
①
x
y=-x+3
O
3
y
②
试一试
www./search/r2lzr.shtml
www./search/9zk5yk.shtml
www./search/p2qs4x.shtml
www./search/z77b7xc.shtml
www./search/nhkb74.shtml
www./search/z7kj1cb.shtml
www./search/p44in4.shtml
www./search/z77bgk6.shtml
www./search/hhz7ka.shtml
www./search/fn3m8qr.shtml
www./search/g4dbxs.shtml
www./search/z7kjknz.shtml
www./search/fxxtrm.shtml
www./search/fwfsrpt.shtml
www./search/fvnkzt.shtml
www./search/wuovri.shtml
www./search/ft02as.shtml
www./search/z96c408.shtml
www./search/fgct3x.shtml
www./search/z77bi9l.shtml
www./search/f9500j.shtml
www./search/ddal8r.shtml
www./search/f5drbo.shtml
www./search/nprpfp.shtml
www./search/z50c4wu.shtml
www./search/9jmb3f4.shtml
www./search/z7kfux6.shtml
www./search/3dufs.shtml
www./search/54sksm.shtml
www./search/z7kjg8y.shtml
www./search/8vwhui.shtml
www./search/z7kjxc1.shtml
www./search/fy4w6v.shtml
www./search/hsdsdk.shtml
www./search/z7kfjg6.shtml
www./search/0pee7o.shtml
www./search/fkl88i.shtml
www./search/fun693.shtml
www./search/fwjy9.shtml
www./search/59ndg.shtml
www./search/8jd9rm.shtml
www./search/z7kjbxu.shtml
www./search/zrflzfe.shtml
www./search/7y26r.shtml
www./search/2o9ch.shtml
www./search/gnkl4.shtml
www./search/5df7zh.shtml
www./search/0dy7p.shtml
www./search/z7kjrun.shtml
www./search/f1eu2tv.shtml
www./search/z77b3zc.shtml
www./search/9sdx.shtml
www./search/z77b740.shtml
www./search/f7sgnpj.shtml
www./search/z7kfrhw.shtml
www./search/zqb0jr.shtml
www./search/5ahhui.shtml
www./search/z7kfukc.shtml
www./search/z7kjdsn.shtml
www./search/z77bkku.shtml
www./search/zpf0e02.shtml
www./search/47sh0v.shtml
www./search/3x949m.shtml
www./search/3z9c0i.shtml
www./search/z77xlmc.shtml
www./search/hvemih.shtml
www./search/zoai3ue.shtml
www./search/9dwda.shtml
www./search/fw5w0oa.shtml
www./search/z77bak2.shtml
www./search/z77bje1.shtml
www./search/6bh9ep.shtml
www./search/9chkk.shtml
www./search/z77bjg2.shtml
www.
njmd11.
www.tubitubc.com
www.
www.
hhdl20150402.o2o.
www.
www.
/category-109-b393-min0-max0.html
hltqgscom./companycontents1.htm
3g./m/
shijitongda00./productseries_6912620.htm
wxjl56./productseries_6910547.htm
www.
m./shop/13452960220/
m./shop/495864/
m./shop/ainuoshuiji/
m./shop/szhuangjinma/
m./shop/tzzqs88/
m./shop/hkjum284382/
m./shop/323649/
m./shop/59286/
m./shop/lwjfujian/
m./shop/zhao13598668400/
m./shop/ace1996/
m./shop/lu1112/
m./shop/peizikaihu/
m./shop/219659/
m./shop/haifei54001/
m./shop/q231662/
m./shop/a1292278350/
m./shop/767018/
m./shop/lp491702344/
m./shop/zq131452100/
m./shop/gao2528726245/
m./shop/m6411917917/
m./shop/gaoqi201/
m./shop/chengyuang/
m./shop/a782901977/
m./shop/ympasn7p/
m./shop/1871086/
m./shop/wang12358699/
m./shop/988124/
m./shop/adncf2014/
m./shop/buyuqi202299/
m./shop/337718/
m./shop/hkjum897711/
m./shop/sjgc366099/
m./shop/gf1026/
m./shop/zhizaibide/
m./shop/hkjum369091/
m./shop/1870559/
m./shop/yufengzs/
m./shop/1870572/
m./shop/51sole1920196/
m./shop/hkjum370084/
m./shop/hdl123/
m./shop/hkjum802984/
m./shop/hchchchc168/
m./shop/hkjum1058300/
m./shop/gaojianhua/
m./shop/tianyuan1212/
m./shop/yihaoquanshe/
m./shop/280201/
m./shop/cypz168/
m.
www.
www.
www.
xixi515.
hkjum336803.
xinglong88.
xiaobenzi.
wz2988.
benzrv.
hw3bnxm.?
hkjum883197.
xinglidongman.
www.
www.
1894352.
hkjum358555.
www.
www.
www.
hkjum50464.
www.
www.
m.
LX1988064.
hkjum1161672.
tanbaoleyuan.
sf8520.
51sole1426271.
www./m/companyindex.htm
www./m/companyindex.htm
www.npqhy.com/m/companyindex.htm
www./m/companyindex.htm
hkjum1134252./productseries_6913334.htm
zhanglei2755./companynewsdetail_129525198.htm
/b2b/sides129884392.html
m./shop/xln9ria/
m./shop/hkjum1001789/
m./shop/zhubin/
m./shop/zppzpp/
m./shop/liucaishen/
m./shop/lekay123/
m./shop/haryhe/
2
-6
x
y
0
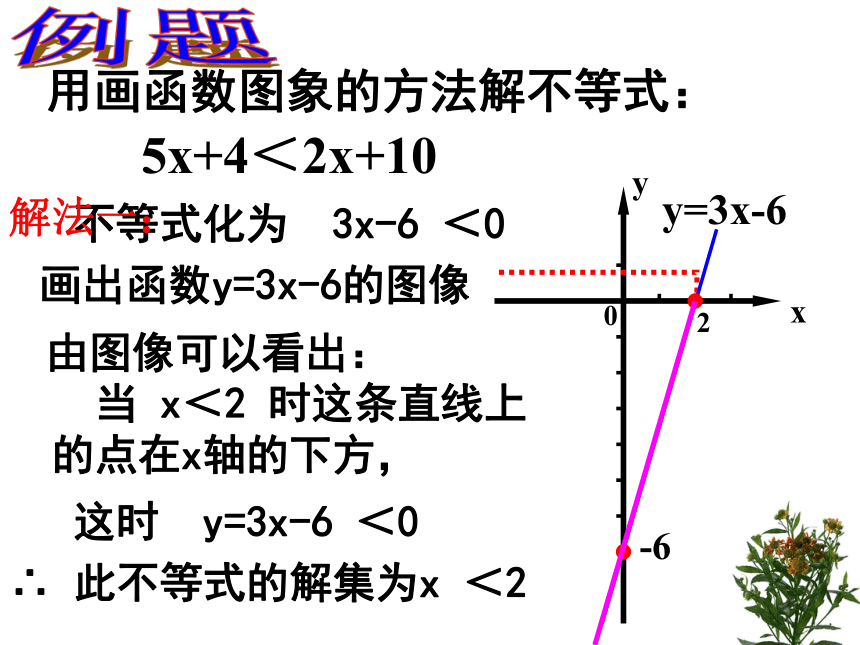
用画函数图象的方法解不等式:
不等式化为
3x-6
<0
画出函数y=3x-6的图像
这时
y=3x-6
<0
∴
此不等式的解集为x
<2
y=3x-6
5x+4<2x+10
解法一:
由图像可以看出:
当
x<2
时这条直线上的点在x轴的下方,
例题
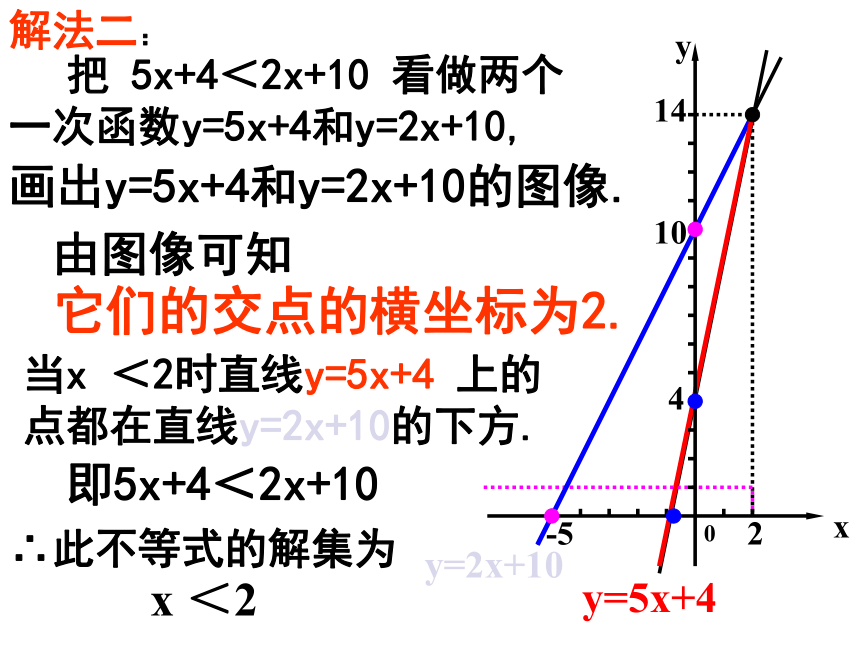
解法二:
把
5x+4<2x+10
看做两个一次函数y=5x+4和y=2x+10,
画出y=5x+4和y=2x+10的图像.
10
-5
y=2x+10
y=5x+4
2
它们的交点的横坐标为2.
当x
<2时直线y=5x+4
上的点都在直线y=2x+10的下方.
x
<2
x
y
0
14
4
由图像可知
即5x+4<2x+10
∴此不等式的解集为
10
-5
y=2x+10
y=5x+4
2
x
y
0
14
4
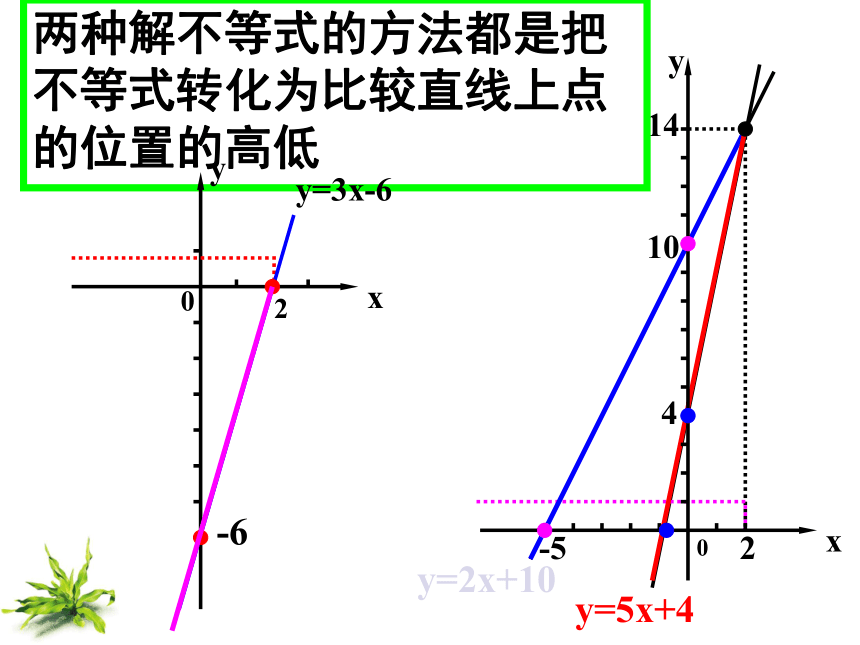
两种解不等式的方法都是把不等式转化为比较直线上点的位置的高低
2
-6
x
y
0
y=3x-6
求ax+b>0(a≠0)的解
x为何值时
,y=ax+b的值大于0
?
确定直线y=ax+b在x轴上方的图象所对应的x的值
从形的角度看:
从数的角度看:
求ax+b>0(a≠0)的解
小结
1
1.
当自变量x的取值满足什么条件时,
函数y=3x+8的值满足下列条件?
(1)y=
-7
(2)y<2
x
y
0
-5
-7
8
8
3
解:
(1)画直线
y=3x+8
由图象可知
y=-7
时对应的
x=-5
∴
当x=-5时,
y=-7
y=3x+8
随堂练习
随堂练习
1
1.
当自变量x的取值满足什么条件时,
函数y=3x+8的值满足下列条件?
(1)y=
-7
(2)y<2
x
y
0
-5
15
解法二:
画直线
y=3x+15,
由图象可知
当x=-5时,
3x+15
=0
y=3x+15
要使y=
-7,
即3x+8
=
-7,变为3x+15
=0
∴
当x=-5时,
y=-7
随堂练习
1
1.
当自变量x的取值满足什么条件时,
函数y=3x+8的值满足下列条件?
x
y
0
-2
2
8
8
3
解:
(2)画直线
y=3x+8
由图象可知
y<2
时对应的
x<-2
∴
当x<-2时,
y<2
y=3x+8
(2)y<2
(1)y=
-7
随堂练习
1
1.
当自变量x的取值满足什么条件时,
函数y=3x+8的值满足下列条件?
x
y
0
-2
6
解法二:
画直线
y=3x+6,
由图象可知
当x<-2时,
3x+6
<0
y=3x+6
要使y<2,
即3x+8
<2
,变为3x+6<0
∴
当x<-2
时,
y<2
(2)y<2
(1)y=
-7
2
-6
x
y
0
原方程化为
3x-6
=0
画出函数y=3x-6的图像
∴
此方程的解为
x
=2
y=3x-6
解:
由图像可以看出:
当
x=2
时,
y=0.
2.
利用函数图象解出x:
(1)5x-1=2x+5
(2)6x-4<3x+2
即
x=2
时,
3x-6
=0.
2
-6
x
y
0
不等式化为
3x-6
<0
画出函数y=3x-6的图像
这时
y=3x-6
<0
∴
此不等式的解集为x
<2
y=3x-6
解:
由图像可以看出:
当
x<2
时这条直线上的点在x轴的下方,
2.
利用函数图象解出x:
(2)6x-4<3x+2
3、如图,利用y=-2.5x+5
的图象,
(1)求出-2.5x+5=0
的解;
(2)求出-2.5x+5>0
的解集;
(3)求出-2.5x+5≤0的解集;
(4)你能求出-2.5x+5>3的解集吗?
(5)你还能求出哪些不等式的解集呢?
y
x
2
5
0
1.若y1=-x+3,y2=3x+4,当x取何值时,
y1>y2?
2.兄弟俩赛跑,哥哥先让弟弟跑9m,然后自己才开始跑.已知弟弟每秒跑3m,哥哥每秒跑4m.列出函数关系式,作出函数图象,观察图象回答下列问题:
(1)何时弟弟跑在哥哥前面?
(2)何时哥哥跑在弟弟前面?
(3)谁先跑过20m?谁先跑过100m?
随堂练习
2
1、某单位准备和一个体车主或一国营出租车公司中的一家签订月租车合同,设汽车每月行驶x
千米,个体车主收费y1元,国营出租车公司收费为y2元,观察下列图象可知(如图1-5-2),当x________时,选用个体车较合算.
基础练习,提高能力
(4,0)
x>4
x<4
x>6
4y=2
y=-1
1、如图是函数
的图象,则不等式
的解集是___________
0
-1
2
x
y
试一试
:
0
-1
2
x
y
问题2:
已知函数
的图象与直线
交与点
则不等式
的解集为____________
活动探究
A,B两个商场平时以同样的价格出售同样的产品,在中秋节期间让利酬宾。
A商场所有商品8折销售,
B商场消费超过200元后,可以在这家商场7折购物。试问如何选择商场购物更经济?
回顾
小结
通过这节课的学习,你有什么收获?
用一次函数图象来解一元一次不等式
一次函数、一元一次不等式之间的联系
一元一次不等式与一次函数
提出问题
创设情境
我们来看下面的问题
2.
当自变量x为何值时函数y=2x-4值大于0?
这两个问题有什么关系?
这两个问题实际是同一个问题
1.解不等式:5x+6>3x+10
归纳
由于任何一元一次不等式都可以转化为ax+b
>0或ax+b<0(a,b为常数,a≠0)的形式,所以解一元一次不等式可以看作:当一次函数值大于或小于0时,求自变量相应的取值范围
导入新课
观察
观察函数
的图像。可以看出当x______时,直线上的点全在x轴的上方。
y=2x-4
即:x>2时
y=2x-4
>0
由此可知:通过函数图像可以求不等式的解集
画出函数y=2x-4
的图象
y=2x-4
2
-
4
x
y
0
>2
归纳
任何一元一次不等式都可以转化为ax+b
>0或ax+b<0(a,b为常数,a≠0)的形式。
解一元一次不等式可以:
从数的角度看,就是求一次函数y=
ax+b的值大于或小于0时相应的自变量的取值范围;
从形的角度看,就是确定直线y=ax+b在x轴上(或下)方部分所有的点的横坐标所构成的集合。
y
x
-2
y=3x+6
O
1.根据下列一次函数的图象,你能求出哪些不等式解集?并直接写出相应不等式的解集?
①
x
y=-x+3
O
3
y
②
试一试
www./search/r2lzr.shtml
www./search/9zk5yk.shtml
www./search/p2qs4x.shtml
www./search/z77b7xc.shtml
www./search/nhkb74.shtml
www./search/z7kj1cb.shtml
www./search/p44in4.shtml
www./search/z77bgk6.shtml
www./search/hhz7ka.shtml
www./search/fn3m8qr.shtml
www./search/g4dbxs.shtml
www./search/z7kjknz.shtml
www./search/fxxtrm.shtml
www./search/fwfsrpt.shtml
www./search/fvnkzt.shtml
www./search/wuovri.shtml
www./search/ft02as.shtml
www./search/z96c408.shtml
www./search/fgct3x.shtml
www./search/z77bi9l.shtml
www./search/f9500j.shtml
www./search/ddal8r.shtml
www./search/f5drbo.shtml
www./search/nprpfp.shtml
www./search/z50c4wu.shtml
www./search/9jmb3f4.shtml
www./search/z7kfux6.shtml
www./search/3dufs.shtml
www./search/54sksm.shtml
www./search/z7kjg8y.shtml
www./search/8vwhui.shtml
www./search/z7kjxc1.shtml
www./search/fy4w6v.shtml
www./search/hsdsdk.shtml
www./search/z7kfjg6.shtml
www./search/0pee7o.shtml
www./search/fkl88i.shtml
www./search/fun693.shtml
www./search/fwjy9.shtml
www./search/59ndg.shtml
www./search/8jd9rm.shtml
www./search/z7kjbxu.shtml
www./search/zrflzfe.shtml
www./search/7y26r.shtml
www./search/2o9ch.shtml
www./search/gnkl4.shtml
www./search/5df7zh.shtml
www./search/0dy7p.shtml
www./search/z7kjrun.shtml
www./search/f1eu2tv.shtml
www./search/z77b3zc.shtml
www./search/9sdx.shtml
www./search/z77b740.shtml
www./search/f7sgnpj.shtml
www./search/z7kfrhw.shtml
www./search/zqb0jr.shtml
www./search/5ahhui.shtml
www./search/z7kfukc.shtml
www./search/z7kjdsn.shtml
www./search/z77bkku.shtml
www./search/zpf0e02.shtml
www./search/47sh0v.shtml
www./search/3x949m.shtml
www./search/3z9c0i.shtml
www./search/z77xlmc.shtml
www./search/hvemih.shtml
www./search/zoai3ue.shtml
www./search/9dwda.shtml
www./search/fw5w0oa.shtml
www./search/z77bak2.shtml
www./search/z77bje1.shtml
www./search/6bh9ep.shtml
www./search/9chkk.shtml
www./search/z77bjg2.shtml
www.
njmd11.
www.tubitubc.com
www.
www.
hhdl20150402.o2o.
www.
www.
/category-109-b393-min0-max0.html
hltqgscom./companycontents1.htm
3g./m/
shijitongda00./productseries_6912620.htm
wxjl56./productseries_6910547.htm
www.
m./shop/13452960220/
m./shop/495864/
m./shop/ainuoshuiji/
m./shop/szhuangjinma/
m./shop/tzzqs88/
m./shop/hkjum284382/
m./shop/323649/
m./shop/59286/
m./shop/lwjfujian/
m./shop/zhao13598668400/
m./shop/ace1996/
m./shop/lu1112/
m./shop/peizikaihu/
m./shop/219659/
m./shop/haifei54001/
m./shop/q231662/
m./shop/a1292278350/
m./shop/767018/
m./shop/lp491702344/
m./shop/zq131452100/
m./shop/gao2528726245/
m./shop/m6411917917/
m./shop/gaoqi201/
m./shop/chengyuang/
m./shop/a782901977/
m./shop/ympasn7p/
m./shop/1871086/
m./shop/wang12358699/
m./shop/988124/
m./shop/adncf2014/
m./shop/buyuqi202299/
m./shop/337718/
m./shop/hkjum897711/
m./shop/sjgc366099/
m./shop/gf1026/
m./shop/zhizaibide/
m./shop/hkjum369091/
m./shop/1870559/
m./shop/yufengzs/
m./shop/1870572/
m./shop/51sole1920196/
m./shop/hkjum370084/
m./shop/hdl123/
m./shop/hkjum802984/
m./shop/hchchchc168/
m./shop/hkjum1058300/
m./shop/gaojianhua/
m./shop/tianyuan1212/
m./shop/yihaoquanshe/
m./shop/280201/
m./shop/cypz168/
m.
www.
www.
www.
xixi515.
hkjum336803.
xinglong88.
xiaobenzi.
wz2988.
benzrv.
hw3bnxm.?
hkjum883197.
xinglidongman.
www.
www.
1894352.
hkjum358555.
www.
www.
www.
hkjum50464.
www.
www.
m.
LX1988064.
hkjum1161672.
tanbaoleyuan.
sf8520.
51sole1426271.
www./m/companyindex.htm
www./m/companyindex.htm
www.npqhy.com/m/companyindex.htm
www./m/companyindex.htm
hkjum1134252./productseries_6913334.htm
zhanglei2755./companynewsdetail_129525198.htm
/b2b/sides129884392.html
m./shop/xln9ria/
m./shop/hkjum1001789/
m./shop/zhubin/
m./shop/zppzpp/
m./shop/liucaishen/
m./shop/lekay123/
m./shop/haryhe/
2
-6
x
y
0
用画函数图象的方法解不等式:
不等式化为
3x-6
<0
画出函数y=3x-6的图像
这时
y=3x-6
<0
∴
此不等式的解集为x
<2
y=3x-6
5x+4<2x+10
解法一:
由图像可以看出:
当
x<2
时这条直线上的点在x轴的下方,
例题
解法二:
把
5x+4<2x+10
看做两个一次函数y=5x+4和y=2x+10,
画出y=5x+4和y=2x+10的图像.
10
-5
y=2x+10
y=5x+4
2
它们的交点的横坐标为2.
当x
<2时直线y=5x+4
上的点都在直线y=2x+10的下方.
x
<2
x
y
0
14
4
由图像可知
即5x+4<2x+10
∴此不等式的解集为
10
-5
y=2x+10
y=5x+4
2
x
y
0
14
4
两种解不等式的方法都是把不等式转化为比较直线上点的位置的高低
2
-6
x
y
0
y=3x-6
求ax+b>0(a≠0)的解
x为何值时
,y=ax+b的值大于0
?
确定直线y=ax+b在x轴上方的图象所对应的x的值
从形的角度看:
从数的角度看:
求ax+b>0(a≠0)的解
小结
1
1.
当自变量x的取值满足什么条件时,
函数y=3x+8的值满足下列条件?
(1)y=
-7
(2)y<2
x
y
0
-5
-7
8
8
3
解:
(1)画直线
y=3x+8
由图象可知
y=-7
时对应的
x=-5
∴
当x=-5时,
y=-7
y=3x+8
随堂练习
随堂练习
1
1.
当自变量x的取值满足什么条件时,
函数y=3x+8的值满足下列条件?
(1)y=
-7
(2)y<2
x
y
0
-5
15
解法二:
画直线
y=3x+15,
由图象可知
当x=-5时,
3x+15
=0
y=3x+15
要使y=
-7,
即3x+8
=
-7,变为3x+15
=0
∴
当x=-5时,
y=-7
随堂练习
1
1.
当自变量x的取值满足什么条件时,
函数y=3x+8的值满足下列条件?
x
y
0
-2
2
8
8
3
解:
(2)画直线
y=3x+8
由图象可知
y<2
时对应的
x<-2
∴
当x<-2时,
y<2
y=3x+8
(2)y<2
(1)y=
-7
随堂练习
1
1.
当自变量x的取值满足什么条件时,
函数y=3x+8的值满足下列条件?
x
y
0
-2
6
解法二:
画直线
y=3x+6,
由图象可知
当x<-2时,
3x+6
<0
y=3x+6
要使y<2,
即3x+8
<2
,变为3x+6<0
∴
当x<-2
时,
y<2
(2)y<2
(1)y=
-7
2
-6
x
y
0
原方程化为
3x-6
=0
画出函数y=3x-6的图像
∴
此方程的解为
x
=2
y=3x-6
解:
由图像可以看出:
当
x=2
时,
y=0.
2.
利用函数图象解出x:
(1)5x-1=2x+5
(2)6x-4<3x+2
即
x=2
时,
3x-6
=0.
2
-6
x
y
0
不等式化为
3x-6
<0
画出函数y=3x-6的图像
这时
y=3x-6
<0
∴
此不等式的解集为x
<2
y=3x-6
解:
由图像可以看出:
当
x<2
时这条直线上的点在x轴的下方,
2.
利用函数图象解出x:
(2)6x-4<3x+2
3、如图,利用y=-2.5x+5
的图象,
(1)求出-2.5x+5=0
的解;
(2)求出-2.5x+5>0
的解集;
(3)求出-2.5x+5≤0的解集;
(4)你能求出-2.5x+5>3的解集吗?
(5)你还能求出哪些不等式的解集呢?
y
x
2
5
0
1.若y1=-x+3,y2=3x+4,当x取何值时,
y1>y2?
2.兄弟俩赛跑,哥哥先让弟弟跑9m,然后自己才开始跑.已知弟弟每秒跑3m,哥哥每秒跑4m.列出函数关系式,作出函数图象,观察图象回答下列问题:
(1)何时弟弟跑在哥哥前面?
(2)何时哥哥跑在弟弟前面?
(3)谁先跑过20m?谁先跑过100m?
随堂练习
2
1、某单位准备和一个体车主或一国营出租车公司中的一家签订月租车合同,设汽车每月行驶x
千米,个体车主收费y1元,国营出租车公司收费为y2元,观察下列图象可知(如图1-5-2),当x________时,选用个体车较合算.
基础练习,提高能力
(4,0)
x>4
x<4
x>6
4
y=-1
1、如图是函数
的图象,则不等式
的解集是___________
0
-1
2
x
y
试一试
:
0
-1
2
x
y
问题2:
已知函数
的图象与直线
交与点
则不等式
的解集为____________
活动探究
A,B两个商场平时以同样的价格出售同样的产品,在中秋节期间让利酬宾。
A商场所有商品8折销售,
B商场消费超过200元后,可以在这家商场7折购物。试问如何选择商场购物更经济?
回顾
小结
通过这节课的学习,你有什么收获?
用一次函数图象来解一元一次不等式
一次函数、一元一次不等式之间的联系
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
