沪教版(上海)九年级数学下册第二十七章《圆与正多边形》单元训练卷(word解析版)
文档属性
| 名称 | 沪教版(上海)九年级数学下册第二十七章《圆与正多边形》单元训练卷(word解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 00:00:00 | ||
图片预览



文档简介
沪教版(上海)九年级数学下册第二十七章《圆与正多边形》单元训练卷
一、单选题
1.下列命题:①直径是弦;②相等的圆心角所对的弧相等;③等弧对等弦;④平分弦的直径垂直于这条弦;⑤半径相等的两个半圆是等弧;⑥弦是圆上两点之间的部分;⑦优弧大于劣弧;⑧圆的切线垂直于半径.错误的个数有( )个
A.2 B.3 C.4 D.5
2.如图,AD⊥BC于点D,AD=4cm,AB=8cm,AC=6cm,则⊙O的直径是( )
A.4cm B.12cm C.8cm D.16cm
3.如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )
A.2 B.2 C.2 D.8
4.如图,中,,点是的内心,则的度数为( )
A. B. C. D.
5.如果两个圆的圆心距为3,其中一个圆的半径长为4,另一个圆的半径长大于1,那么这两个圆的位置关系不可能是( )
A.内含 B.内切 C.外切 D.相交
6.如图,将矩形ABCD绕着点A逆时针旋转得到矩形AEFG,点B的对应点E落在边CD上,且DE=EF,若AD=3,则的长为( )
A.π B.π C.π D.π
7.如图,AB为⊙O的切线,切点为B,连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD.若∠A=30°,⊙O的半径为2,则图中阴影部分的面积为( )
A. B. C. D.
8.如图,直线AB切圆O于点B,直线AC过圆心O,下列结论中:①∠DBC=90°;②∠ABO=90°;③∠BCD=∠AOB;④∠ABD=∠OBC,其中正确结论的个数是( )
A.1 B.2 C.3 D.4
9.如图,的直径的长为,弦长为,的平分线交于,则长为( )
A.7 B.7 C.8 D.9
10.如图,AB是⊙O的直径,弦DC交AB于E,过C作⊙O的切线交DB的延长线于M,若AB=4,∠ADC=45°,∠M=75°,则CD的长为( )
A. B.2 C. D.
11.如图,直角梯形ABCD中,∠BAD=∠CDA=90°,AB=,CD=2,过A,B,D三点的☉O分别交BC,CD于点E,M,且CE=2,下列结论:①DM=CM;②弧AB=弧EM;③☉O的直径为2;④AE=.其中正确的结论是( )
A.①②③ B.①②④ C.①③④ D.①②③④
12.如图.Rt△ABC内接于⊙O,BC为直径,AB=4,AC=3,D是弧AB 的中点,CD与AB的交点为E,则 等于(?? )
A.4????????????????????????????? B.3.5 C.3 D.2.8
二、填空题
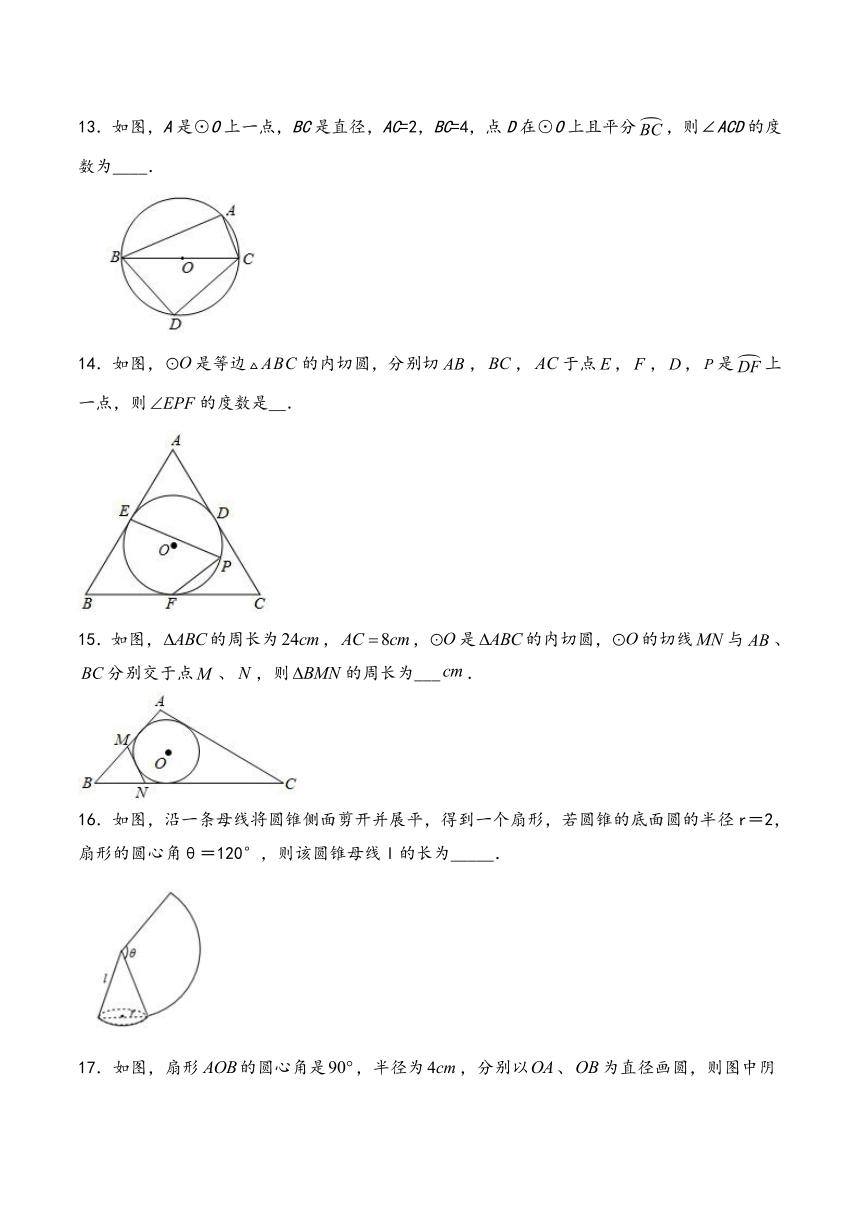
13.如图,A是⊙O上一点,BC是直径,AC=2,BC=4,点D在⊙O上且平分,则∠ACD的度数为____.
14.如图,是等边的内切圆,分别切,,于点,,,是上一点,则的度数是__.
15.如图,的周长为,,是的内切圆,的切线与、分别交于点、,则的周长为___.
16.如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2,扇形的圆心角θ=120°,则该圆锥母线l的长为_____.
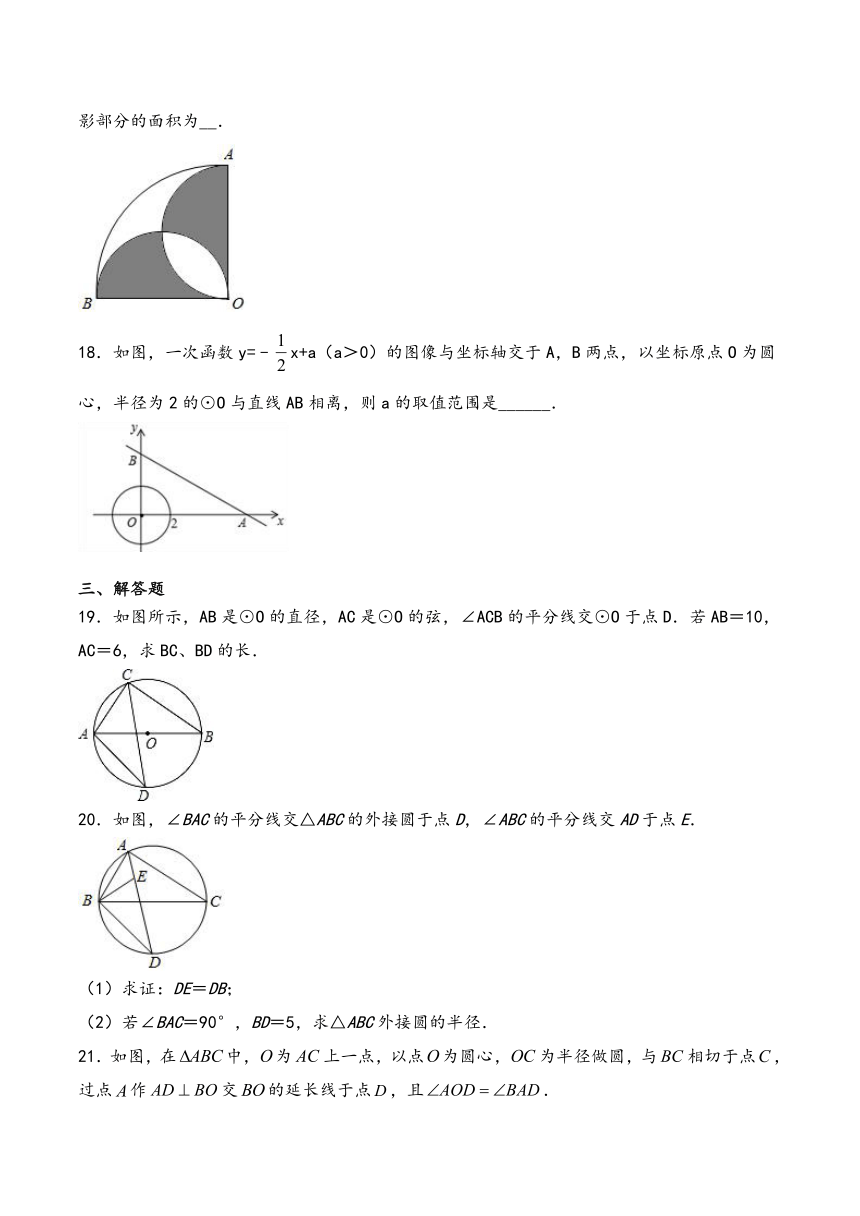
17.如图,扇形的圆心角是,半径为,分别以、为直径画圆,则图中阴影部分的面积为__.
18.如图,一次函数y=﹣x+a(a>0)的图像与坐标轴交于A,B两点,以坐标原点O为圆心,半径为2的⊙O与直线AB相离,则a的取值范围是______.
三、解答题
19.如图所示,AB是⊙O的直径,AC是⊙O的弦,∠ACB的平分线交⊙O于点D.若AB=10,AC=6,求BC、BD的长.
20.如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E.
(1)求证:DE=DB;
(2)若∠BAC=90°,BD=5,求△ABC外接圆的半径.
21.如图,在中,为上一点,以点为圆心,为半径做圆,与相切于点,过点作交的延长线于点,且.
(1)求证:为的切线;
(2)若,,求的长.
22.如图,是的直径,点在的延长线上,平分交于点,于点.
(1)求证:直线是的切线.
(2)如果,,求线段的长.
23.如图,已知AB是⊙O的直径,C,D是⊙O上的点,,交AD于点E,连结BC.
(1)求证:AE=ED;
(2)若AB=6,∠CBD=30°,求图中阴影部分的面积.
24.如图,△ABC中,AB=AC,以AB为直径作⊙O,分别交BC、AC于点D、E.
(1)求证:BD=CD;
(2)若∠ABC=63°,求∠BDE的度数;
(3)过点D作⊙O的切线,交AB的延长线于点F,当AO=DF=4时,求图中阴影部分的面积.
25.如图,△ABC内接于半圆,AB是直径,过A作直线MN,∠MAC=∠ABC,D是弧AC的中点,连接BD交AC于G,过D作DE⊥AB于E,交AC于F.
(1)求证:MN是半圆的切线;
(2)作DH⊥BC交BC的延长线于点H,连接CD,试判断线段AE与线段CH的数量关系,并说明理由.
(3)若BC=4,AB=6,试求AE的长.
参考答案
1.D
解:①直径是弦.正确;
②相等的圆心角所对的弧相等.错误,应该是在同圆或等圆中;
③等弧对等弦,正确;
④平分弦的直径垂直于弦.错误,此弦非直径;
⑤半径相等的两个半圆是等弧.正确;
⑥弦是圆上任意两点之间的连线,所以⑥错误;
⑦在同圆或等圆中,优弧大于劣弧,⑦错误;
⑧圆的切线垂直于过切点的半径,⑧错误
所以,错误的个数有5个,
2.B
解:延长交于圆上点E,连接BE,则∠E=∠C,
为的直径,
∠ADC=∠ABE=90°
∴△ABE∽△ADC
∴
AD=4cm,AB=8cm,AC=6cm,
解得AE=12cm.
的直径为
3.B
连接BE,
设⊙O半径为r,则OA=OD=r,OC=r﹣2,
∵OD⊥AB,
∴∠ACO=90°,
AC=BC=AB=4,
在Rt△ACO中,由勾股定理得: ,
解得:r=5,
∴AE=2r=10,
∵AE为⊙O的直径,
∴∠ABE=90°,
由勾股定理得:BE=6,
在Rt△ECB中, .
4.D
解:∵,
∴,
∵点是的内心,
∴BO平分∠ABC,CO平分∠ACB,
∴,,
∴,
∴.
5.C
解:∵一个圆的半径R为4,另一个圆的半径r大于1,
∴R﹣r<4﹣1,R+r>5
即:R﹣r<3,
∵圆心距为3,
∴两圆不可能外切,
6.A
连接AC、AF,
由旋转的性质可知,BC=EF,AB=AE.
∵DE=EF,
∴DE=BC=AD.
在Rt△ADE中,DE=AD,
∴∠DAE=45°,AE==,
∴∠EAB=90°﹣45°=45°,即旋转角为45°,
∴∠FAC=45°.
在Rt△ABC中,AC==9,
∴的长=,
故选:A.
7.A
解:过O点作OE⊥CD于E,
∵AB为⊙O的切线,
∴∠ABO=90°,
∵∠A=30°,
∴∠AOB=60°,
∴∠COD=120°,∠OCD=∠ODC=30°,
∵⊙O的半径为2,
∴OE=1,CE=DE=,
∴CD=2,
∴图中阴影部分的面积为:=.
故选:A.
8.D
∵DC是⊙O的直径,∴∠DBC=90°,故①正确;
∵AB切圆O于点B,∴∠ABO=90°,故②正确;
∵OB=OC,∴∠BCD=∠CBO,
∵∠AOB=∠BCD+∠CBO,∴∠BCD= ∠AOB,故③正确;
∵∠ABO=90°,∴∠ABD=90°﹣∠DBO,
∵∠DBC=90°,∴∠OBC=90°﹣∠DBO,
∴∠ABD=∠OBC,故④正确,
9.B
作DF⊥CA,垂足F在CA的延长线上,作DG⊥CB于点G,连接DA,DB,
∵CD平分∠ACB,
∴∠ACD=∠BCD
∴DF=DG,,
∴DA=DB,
∵∠AFD=∠BGD=90°,
∴△AFD≌△BGD,
∴AF=BG.
易证△CDF≌△CDG,
∴CF=CG,
∵AC=6,BC=8,
∴AF=1,
∴CF=7,
∵△CDF是等腰直角三角形,
∴CD=7,
故选B.
10.D
解:连接OC,过O作OF⊥CD,利用垂径定理得到F为CD的中点,
∵CM为圆O的切线,
∴∠OCM=90°,
∵∠ADC与∠AOC都对弧AC,
∴∠AOC=2∠ADC=90°,
∴∠CDM=∠BOC=45°,
∵∠M=75°,
∴∠DCM=60°,
∴∠OCF=30°,
在Rt△OCF中,OC=2,
∴CF=OC?cos∠OCF=,
则CD=2CF=2.
故选D.
11.B
连接BD,BM,AM,EM,DE,
∵∠BAD=90°,
∴BD为圆的直径,
∴∠BMD=90°,
∴∠BAD=∠CDA=∠BMD=90°,
∴四边形ABMD矩形,
∴AB=DM,
又∵CD=2AB,
∴CD=2DM,即DM=MC;
故选项①正确;
在Rt△DEC中,M是DC中点,
∴EM=DM=CD=,
∴弧EM=弧DM,
又∵AB=DM,
∴弧AB=弧DM,
∴弧AB=弧EM,
故选项②正确;
∵AB∥MC,AB=MC,
∴四边形ABCM是平行四边形,
∴AM=BC,又BD=AM,
∴BD=BC,
∵BD是直径,
∴∠BED=90°,即∠DEC=90°,
又EC=2,DC=2,
根据勾股定理得:DE==2,
设BE=x,BD=BC=BE+EC=x+2,
在Rt△BDE中,根据勾股定理得:BE2+DE2=BD2,即x2+20=(x+2)2,
解得:x=4,
∴BD=6,故选项③错误;
在Rt△AEM中,AM=6,EM=,
根据勾股定理得:AE==;
故选项④正确;
则正确的选项为:①②④.
12.C
如图,连接DO,交AB于点F,
∵D是的中点,
∴DO⊥AB,AF=BF,
∵AB=4,
∴AF=BF=2,
∴FO是△ABC的中位线,AC∥DO,
∵BC为直径,AB=4,AC=3,
∴BC=5,FO=AC=1.5,
∴DO=2.5,
∴DF=2.5﹣1.5=1,
∵AC∥DO,
∴△DEF∽△CEA,
∴,
∴ =3,
故选C.
13.105°
解:∵BC是直径,
∴,
∵,,
∴,
∴,
∵D是中点,
∴,
∴,
∴.
14.
解:如图,连接、,
是等边的内切圆,
,,
∴,
,
为等边三角形,
∴,
,
.
15.8
设与与各边的切点分别为、、,与相切于点,如图,
,,,
,即,
,
的周长为24,
,
,
即,
,
的切线与、分别交于点、,
,,
的周长.
16.6.
解:根据题意得2π×2=,
解得,l=6,
即该圆锥母线l的长为6.
17.
解:如图,连接,过点作,,
,,
是等腰直角三角形,
是直径,
,
是等腰直角三角形,
,
,,
,
,
与弦围成的弓形的面积等于与弦所围成的弓形面积,
同理可得,与弦围成的弓形的面积等于与弦所围成的弓形面积,
.
18.a﹥
(1)当y=0时,﹣x+a,解得x=2a,则A(2a,0),
当x=0时,y=?x+a=a,则B(0,a),
在Rt△ABO中,AB==a,
过O点作OH⊥AB于H,如图,
∵?OH?AB=?OB?OA,
∴OH==,
∵半径为2的O与直线AB相离,
所以OH>2,即>2,
所以a>
故答案为a>.
19.BC=8,BD=5
解:连接BD,如图,
∵AB是直径,
∴∠ACB=∠ADB=90°,
在Rt△ABC中,AB=10,AC=6,
∴BC===8,即BC=8;
∵∠ACB的平分线交⊙O于点D,
∴∠DCA=∠BCD,
∴,
∴AD=BD,
∴在Rt△ABD中,AD=BD=AB=×10=5,即BD=5.
【点睛】
本题考查了勾股定理,圆周角定理,解题的关键是求出∠ACB=∠ADB=90°.
20.
(1)证明:∵AD平分∠BAC,BE平分∠ABC,
∴∠ABE=∠CBE,∠BAE=∠CAD,
∴,
∴∠DBC=∠CAD,
∴∠DBC=∠BAE,
∵∠DBE=∠CBE+∠DBC,∠DEB=∠ABE+∠BAE,
∴∠DBE=∠DEB,
∴DE=DB;
(2)解:连接CD,如图所示:
由(1)得:,
∴CD=BD=5,
∵∠BAC=90°,
∴BC是直径,
∴∠BDC=90°,
∴BC5,
∴△ABC外接圆的半径:r.
21.
解:(1)过点作于点,
于点,
,
,,
,
,
又为的切线,
,
,
,
,
在和中,
,
,
,
,
是的切线;
(2),,
,
,,
,
则,
由(1)知,
,
,
,
,,
,,
,
,即,
.
22.
证明:(1)如图1,连接,
,
,
平分,
,
,
,
,
,
,
,
是的切线;
(2)解:如图2,连接,
,
,
是的直径,
,
,
,
,
,
,
,
∵,,
,
,
,
设,则,
∵在Rt△ABC中,,
,
解得,.
,
,,
,
,
,
.
23.
(1)∵AB是的直径,
∴,即点O是AB的中点,
∵,
∴是的中位线,
点E是AD的中点,
∴;
(2)如图,连接OD,
∵AB是的直径,,
,,
∵,
,即,
又是的半径,
,
,
,,
在中,,
OD是的斜边AB上的中线,
,
又,
,
则图中阴影部分的面积为.
24.
解:(1)连接AD,
∵AB是⊙O的直径,故∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴BD=CD;
(2)∵AB=AC,
∴,
∵∠ABC=63°,
∴∠BAC=180°﹣63°﹣63°=54°;
∵四边形ABDE是圆内接四边形
∴∠BDE=180°﹣54°=126°
(3)连接OD,
∵DF是圆的切线,
∴∠ODF=90°,
在⊙O中,OA=OD,
而OA=DF=4,则DO=DF=4,
故∠FOD=45°,
∴S阴影=S△ODF﹣S扇形OBD4×48﹣2π.
25.
解:(1)如图所示,
∵AB是直径,∴∠ACB=90°,∴∠CAB+∠ABC=90°,
∵∠MAC=∠ABC,∴∠CAB+∠MAC=90°,
即∠MAB=90°,
∴MN是半圆的切线;
(2)AE=CH,理由如下:
连接AD,
∵D是的中点,∴AD=CD,∠HBD=∠ABD,
∵DE⊥AB,DH⊥BC,∴DE=DH,且∠AED=∠DHC,
在Rt△ADE和Rt△CDH中, ,∴Rt△ADE≌Rt△CDH(HL),
∴AE=CH;
(3)由(2)知DH=DE,∠DHB=∠DEB=90°,
在△RtDBH和Rt△DBE中, ,∴△RtDBH≌Rt△DBE(HL),
∴BE=BH,∴BA﹣AE=BC+CH,且AE=CH,∴BA﹣AE=BC+AE,
又∵AB=6,BC=4,∴6﹣AE=4+AE,
∴AE=1.
一、单选题
1.下列命题:①直径是弦;②相等的圆心角所对的弧相等;③等弧对等弦;④平分弦的直径垂直于这条弦;⑤半径相等的两个半圆是等弧;⑥弦是圆上两点之间的部分;⑦优弧大于劣弧;⑧圆的切线垂直于半径.错误的个数有( )个
A.2 B.3 C.4 D.5
2.如图,AD⊥BC于点D,AD=4cm,AB=8cm,AC=6cm,则⊙O的直径是( )
A.4cm B.12cm C.8cm D.16cm
3.如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )
A.2 B.2 C.2 D.8
4.如图,中,,点是的内心,则的度数为( )
A. B. C. D.
5.如果两个圆的圆心距为3,其中一个圆的半径长为4,另一个圆的半径长大于1,那么这两个圆的位置关系不可能是( )
A.内含 B.内切 C.外切 D.相交
6.如图,将矩形ABCD绕着点A逆时针旋转得到矩形AEFG,点B的对应点E落在边CD上,且DE=EF,若AD=3,则的长为( )
A.π B.π C.π D.π
7.如图,AB为⊙O的切线,切点为B,连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD.若∠A=30°,⊙O的半径为2,则图中阴影部分的面积为( )
A. B. C. D.
8.如图,直线AB切圆O于点B,直线AC过圆心O,下列结论中:①∠DBC=90°;②∠ABO=90°;③∠BCD=∠AOB;④∠ABD=∠OBC,其中正确结论的个数是( )
A.1 B.2 C.3 D.4
9.如图,的直径的长为,弦长为,的平分线交于,则长为( )
A.7 B.7 C.8 D.9
10.如图,AB是⊙O的直径,弦DC交AB于E,过C作⊙O的切线交DB的延长线于M,若AB=4,∠ADC=45°,∠M=75°,则CD的长为( )
A. B.2 C. D.
11.如图,直角梯形ABCD中,∠BAD=∠CDA=90°,AB=,CD=2,过A,B,D三点的☉O分别交BC,CD于点E,M,且CE=2,下列结论:①DM=CM;②弧AB=弧EM;③☉O的直径为2;④AE=.其中正确的结论是( )
A.①②③ B.①②④ C.①③④ D.①②③④
12.如图.Rt△ABC内接于⊙O,BC为直径,AB=4,AC=3,D是弧AB 的中点,CD与AB的交点为E,则 等于(?? )
A.4????????????????????????????? B.3.5 C.3 D.2.8
二、填空题
13.如图,A是⊙O上一点,BC是直径,AC=2,BC=4,点D在⊙O上且平分,则∠ACD的度数为____.
14.如图,是等边的内切圆,分别切,,于点,,,是上一点,则的度数是__.
15.如图,的周长为,,是的内切圆,的切线与、分别交于点、,则的周长为___.
16.如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2,扇形的圆心角θ=120°,则该圆锥母线l的长为_____.
17.如图,扇形的圆心角是,半径为,分别以、为直径画圆,则图中阴影部分的面积为__.
18.如图,一次函数y=﹣x+a(a>0)的图像与坐标轴交于A,B两点,以坐标原点O为圆心,半径为2的⊙O与直线AB相离,则a的取值范围是______.
三、解答题
19.如图所示,AB是⊙O的直径,AC是⊙O的弦,∠ACB的平分线交⊙O于点D.若AB=10,AC=6,求BC、BD的长.
20.如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E.
(1)求证:DE=DB;
(2)若∠BAC=90°,BD=5,求△ABC外接圆的半径.
21.如图,在中,为上一点,以点为圆心,为半径做圆,与相切于点,过点作交的延长线于点,且.
(1)求证:为的切线;
(2)若,,求的长.
22.如图,是的直径,点在的延长线上,平分交于点,于点.
(1)求证:直线是的切线.
(2)如果,,求线段的长.
23.如图,已知AB是⊙O的直径,C,D是⊙O上的点,,交AD于点E,连结BC.
(1)求证:AE=ED;
(2)若AB=6,∠CBD=30°,求图中阴影部分的面积.
24.如图,△ABC中,AB=AC,以AB为直径作⊙O,分别交BC、AC于点D、E.
(1)求证:BD=CD;
(2)若∠ABC=63°,求∠BDE的度数;
(3)过点D作⊙O的切线,交AB的延长线于点F,当AO=DF=4时,求图中阴影部分的面积.
25.如图,△ABC内接于半圆,AB是直径,过A作直线MN,∠MAC=∠ABC,D是弧AC的中点,连接BD交AC于G,过D作DE⊥AB于E,交AC于F.
(1)求证:MN是半圆的切线;
(2)作DH⊥BC交BC的延长线于点H,连接CD,试判断线段AE与线段CH的数量关系,并说明理由.
(3)若BC=4,AB=6,试求AE的长.
参考答案
1.D
解:①直径是弦.正确;
②相等的圆心角所对的弧相等.错误,应该是在同圆或等圆中;
③等弧对等弦,正确;
④平分弦的直径垂直于弦.错误,此弦非直径;
⑤半径相等的两个半圆是等弧.正确;
⑥弦是圆上任意两点之间的连线,所以⑥错误;
⑦在同圆或等圆中,优弧大于劣弧,⑦错误;
⑧圆的切线垂直于过切点的半径,⑧错误
所以,错误的个数有5个,
2.B
解:延长交于圆上点E,连接BE,则∠E=∠C,
为的直径,
∠ADC=∠ABE=90°
∴△ABE∽△ADC
∴
AD=4cm,AB=8cm,AC=6cm,
解得AE=12cm.
的直径为
3.B
连接BE,
设⊙O半径为r,则OA=OD=r,OC=r﹣2,
∵OD⊥AB,
∴∠ACO=90°,
AC=BC=AB=4,
在Rt△ACO中,由勾股定理得: ,
解得:r=5,
∴AE=2r=10,
∵AE为⊙O的直径,
∴∠ABE=90°,
由勾股定理得:BE=6,
在Rt△ECB中, .
4.D
解:∵,
∴,
∵点是的内心,
∴BO平分∠ABC,CO平分∠ACB,
∴,,
∴,
∴.
5.C
解:∵一个圆的半径R为4,另一个圆的半径r大于1,
∴R﹣r<4﹣1,R+r>5
即:R﹣r<3,
∵圆心距为3,
∴两圆不可能外切,
6.A
连接AC、AF,
由旋转的性质可知,BC=EF,AB=AE.
∵DE=EF,
∴DE=BC=AD.
在Rt△ADE中,DE=AD,
∴∠DAE=45°,AE==,
∴∠EAB=90°﹣45°=45°,即旋转角为45°,
∴∠FAC=45°.
在Rt△ABC中,AC==9,
∴的长=,
故选:A.
7.A
解:过O点作OE⊥CD于E,
∵AB为⊙O的切线,
∴∠ABO=90°,
∵∠A=30°,
∴∠AOB=60°,
∴∠COD=120°,∠OCD=∠ODC=30°,
∵⊙O的半径为2,
∴OE=1,CE=DE=,
∴CD=2,
∴图中阴影部分的面积为:=.
故选:A.
8.D
∵DC是⊙O的直径,∴∠DBC=90°,故①正确;
∵AB切圆O于点B,∴∠ABO=90°,故②正确;
∵OB=OC,∴∠BCD=∠CBO,
∵∠AOB=∠BCD+∠CBO,∴∠BCD= ∠AOB,故③正确;
∵∠ABO=90°,∴∠ABD=90°﹣∠DBO,
∵∠DBC=90°,∴∠OBC=90°﹣∠DBO,
∴∠ABD=∠OBC,故④正确,
9.B
作DF⊥CA,垂足F在CA的延长线上,作DG⊥CB于点G,连接DA,DB,
∵CD平分∠ACB,
∴∠ACD=∠BCD
∴DF=DG,,
∴DA=DB,
∵∠AFD=∠BGD=90°,
∴△AFD≌△BGD,
∴AF=BG.
易证△CDF≌△CDG,
∴CF=CG,
∵AC=6,BC=8,
∴AF=1,
∴CF=7,
∵△CDF是等腰直角三角形,
∴CD=7,
故选B.
10.D
解:连接OC,过O作OF⊥CD,利用垂径定理得到F为CD的中点,
∵CM为圆O的切线,
∴∠OCM=90°,
∵∠ADC与∠AOC都对弧AC,
∴∠AOC=2∠ADC=90°,
∴∠CDM=∠BOC=45°,
∵∠M=75°,
∴∠DCM=60°,
∴∠OCF=30°,
在Rt△OCF中,OC=2,
∴CF=OC?cos∠OCF=,
则CD=2CF=2.
故选D.
11.B
连接BD,BM,AM,EM,DE,
∵∠BAD=90°,
∴BD为圆的直径,
∴∠BMD=90°,
∴∠BAD=∠CDA=∠BMD=90°,
∴四边形ABMD矩形,
∴AB=DM,
又∵CD=2AB,
∴CD=2DM,即DM=MC;
故选项①正确;
在Rt△DEC中,M是DC中点,
∴EM=DM=CD=,
∴弧EM=弧DM,
又∵AB=DM,
∴弧AB=弧DM,
∴弧AB=弧EM,
故选项②正确;
∵AB∥MC,AB=MC,
∴四边形ABCM是平行四边形,
∴AM=BC,又BD=AM,
∴BD=BC,
∵BD是直径,
∴∠BED=90°,即∠DEC=90°,
又EC=2,DC=2,
根据勾股定理得:DE==2,
设BE=x,BD=BC=BE+EC=x+2,
在Rt△BDE中,根据勾股定理得:BE2+DE2=BD2,即x2+20=(x+2)2,
解得:x=4,
∴BD=6,故选项③错误;
在Rt△AEM中,AM=6,EM=,
根据勾股定理得:AE==;
故选项④正确;
则正确的选项为:①②④.
12.C
如图,连接DO,交AB于点F,
∵D是的中点,
∴DO⊥AB,AF=BF,
∵AB=4,
∴AF=BF=2,
∴FO是△ABC的中位线,AC∥DO,
∵BC为直径,AB=4,AC=3,
∴BC=5,FO=AC=1.5,
∴DO=2.5,
∴DF=2.5﹣1.5=1,
∵AC∥DO,
∴△DEF∽△CEA,
∴,
∴ =3,
故选C.
13.105°
解:∵BC是直径,
∴,
∵,,
∴,
∴,
∵D是中点,
∴,
∴,
∴.
14.
解:如图,连接、,
是等边的内切圆,
,,
∴,
,
为等边三角形,
∴,
,
.
15.8
设与与各边的切点分别为、、,与相切于点,如图,
,,,
,即,
,
的周长为24,
,
,
即,
,
的切线与、分别交于点、,
,,
的周长.
16.6.
解:根据题意得2π×2=,
解得,l=6,
即该圆锥母线l的长为6.
17.
解:如图,连接,过点作,,
,,
是等腰直角三角形,
是直径,
,
是等腰直角三角形,
,
,,
,
,
与弦围成的弓形的面积等于与弦所围成的弓形面积,
同理可得,与弦围成的弓形的面积等于与弦所围成的弓形面积,
.
18.a﹥
(1)当y=0时,﹣x+a,解得x=2a,则A(2a,0),
当x=0时,y=?x+a=a,则B(0,a),
在Rt△ABO中,AB==a,
过O点作OH⊥AB于H,如图,
∵?OH?AB=?OB?OA,
∴OH==,
∵半径为2的O与直线AB相离,
所以OH>2,即>2,
所以a>
故答案为a>.
19.BC=8,BD=5
解:连接BD,如图,
∵AB是直径,
∴∠ACB=∠ADB=90°,
在Rt△ABC中,AB=10,AC=6,
∴BC===8,即BC=8;
∵∠ACB的平分线交⊙O于点D,
∴∠DCA=∠BCD,
∴,
∴AD=BD,
∴在Rt△ABD中,AD=BD=AB=×10=5,即BD=5.
【点睛】
本题考查了勾股定理,圆周角定理,解题的关键是求出∠ACB=∠ADB=90°.
20.
(1)证明:∵AD平分∠BAC,BE平分∠ABC,
∴∠ABE=∠CBE,∠BAE=∠CAD,
∴,
∴∠DBC=∠CAD,
∴∠DBC=∠BAE,
∵∠DBE=∠CBE+∠DBC,∠DEB=∠ABE+∠BAE,
∴∠DBE=∠DEB,
∴DE=DB;
(2)解:连接CD,如图所示:
由(1)得:,
∴CD=BD=5,
∵∠BAC=90°,
∴BC是直径,
∴∠BDC=90°,
∴BC5,
∴△ABC外接圆的半径:r.
21.
解:(1)过点作于点,
于点,
,
,,
,
,
又为的切线,
,
,
,
,
在和中,
,
,
,
,
是的切线;
(2),,
,
,,
,
则,
由(1)知,
,
,
,
,,
,,
,
,即,
.
22.
证明:(1)如图1,连接,
,
,
平分,
,
,
,
,
,
,
,
是的切线;
(2)解:如图2,连接,
,
,
是的直径,
,
,
,
,
,
,
,
∵,,
,
,
,
设,则,
∵在Rt△ABC中,,
,
解得,.
,
,,
,
,
,
.
23.
(1)∵AB是的直径,
∴,即点O是AB的中点,
∵,
∴是的中位线,
点E是AD的中点,
∴;
(2)如图,连接OD,
∵AB是的直径,,
,,
∵,
,即,
又是的半径,
,
,
,,
在中,,
OD是的斜边AB上的中线,
,
又,
,
则图中阴影部分的面积为.
24.
解:(1)连接AD,
∵AB是⊙O的直径,故∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴BD=CD;
(2)∵AB=AC,
∴,
∵∠ABC=63°,
∴∠BAC=180°﹣63°﹣63°=54°;
∵四边形ABDE是圆内接四边形
∴∠BDE=180°﹣54°=126°
(3)连接OD,
∵DF是圆的切线,
∴∠ODF=90°,
在⊙O中,OA=OD,
而OA=DF=4,则DO=DF=4,
故∠FOD=45°,
∴S阴影=S△ODF﹣S扇形OBD4×48﹣2π.
25.
解:(1)如图所示,
∵AB是直径,∴∠ACB=90°,∴∠CAB+∠ABC=90°,
∵∠MAC=∠ABC,∴∠CAB+∠MAC=90°,
即∠MAB=90°,
∴MN是半圆的切线;
(2)AE=CH,理由如下:
连接AD,
∵D是的中点,∴AD=CD,∠HBD=∠ABD,
∵DE⊥AB,DH⊥BC,∴DE=DH,且∠AED=∠DHC,
在Rt△ADE和Rt△CDH中, ,∴Rt△ADE≌Rt△CDH(HL),
∴AE=CH;
(3)由(2)知DH=DE,∠DHB=∠DEB=90°,
在△RtDBH和Rt△DBE中, ,∴△RtDBH≌Rt△DBE(HL),
∴BE=BH,∴BA﹣AE=BC+CH,且AE=CH,∴BA﹣AE=BC+AE,
又∵AB=6,BC=4,∴6﹣AE=4+AE,
∴AE=1.
