沪科版(2012)初中数学九年级下册-24.1 旋转 教案
文档属性
| 名称 | 沪科版(2012)初中数学九年级下册-24.1 旋转 教案 |
|
|
| 格式 | zip | ||
| 文件大小 | 477.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-15 00:00:00 | ||
图片预览


文档简介
课题:24.1 旋转(第3课时)
————中心对称图形
一、教学目标
1.知识与技能
(1)认识中心对称图形的有关概念;
(2)能判断某图形是不是中心对称图形.
2.过程与方法
经历观察、发现、探究中心对称图形的有关概念和基本性质,判断某图形是否是中心对称图形.
3.情感、态度与价值观
让学生体验到数学与生活的紧密联系;欣赏生活中的对称美,发展学生的美感
二、教学重难点
重点:中心对称图形的概念和性质.
难点:中心对称与中心对称图形的区别与联系.
三、教学活动设计
(一)知识回顾:
1、什么叫做中心对称?中心对称有哪些性质?
2、怎样作一个图形关于某一个定点的中心对称的图形?
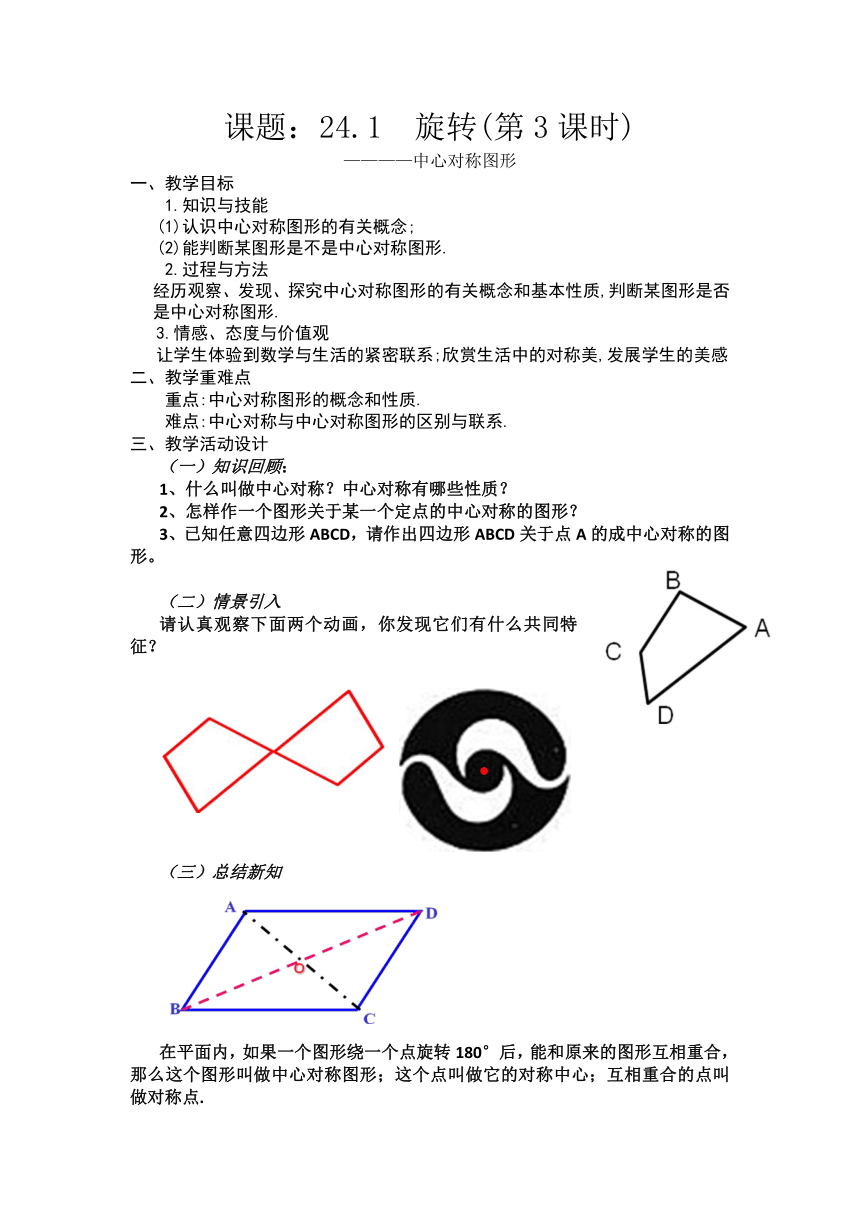
3、已知任意四边形ABCD,请作出四边形ABCD关于点A的成中心对称的图形。
(二)情景引入
请认真观察下面两个动画,你发现它们有什么共同特征?
(三)总结新知
在平面内,如果一个图形绕一个点旋转180°后,能和原来的图形互相重合,那么这个图形叫做中心对称图形;这个点叫做它的对称中心;互相重合的点叫做对称点.
(四)探究
中心对称图形是旋转对称图形的一种特殊情形
(五)练习
判断下列图形是否是中心对称图形?如果是,那么对称中心在哪?
判定中心对称图形的方法:若图形上存在这样一个点,使整个图形绕着这个点旋转180°后能够与原来的图形重合,则这个图形就是中心对称图形。
下面的扑克牌中,哪些牌面是中心对称图形?
(六)思考
我们已经知道平行四边形是中心对称图形,现过对称中心任意画一直线将其分成两部分,这两部分面积有何关系?每一对对应点的连线有什么特点?
中心对称图形的性质:过对称中心的任意一条直线将中心对称图形分成面积相等的两部分;每一对对应点的连线都经过对称中心并且被对称中心平分。
(七)应用提升
张老汉有一块田地如图所示,他想田分给两个儿子,儿子提出:
⑴分割的面积应相等;
⑵最好把分割线做成一条水渠,便于灌溉。
你能帮助张老汉画出这条分割线吗?
(八)总结提升
1、中心对称与中心对称图形有什么区别与联系?
名称
中心对称
中心对称图形
定义
把一个图形绕着某一个点旋转180,如果他能够与另一个图形重合,那么就说这两个图形关于这点对称,这个点叫做对称中心,两个图形关于点对称也称中心对称
如果一个图形绕着一个点旋转180后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形
性质
①两个图形可完全重合;
②对应点连线都经过对称中心,并且被对称中心平分
③对应边平行或在同一条直线上
①对应点连线都经过对称中心,并且被对称中心平分
②过对称中心的任意一条直线将中心对称图形分成面积相等的两部分
区别
两个图形的位置关系
具有某种性质的一个图形
联系
若把中心对称图形的两部分分别看作两个图形,则它们成中心对称,若把中心对称的两个图形看作一个整体,则成为中心对称图形。
巩固应用
观察下面的几个图形哪些是中心对称?哪些是中心对称图形?
2、轴对称图形与中心对称图形有什么区别?
轴对称图形
中心对称图形
有一条对称轴——直线
有一个对称中心——点
图形沿轴对折
图形绕这个点旋转180O
对折部分与另一部分重合
旋转后与原图形重合
巩固练习
观察图形,并回答下面的问题:
(1)哪些只是轴对称图形?
(2)哪些只是中心对称图形?
(3)哪些既是轴对称图形,又是中心对称图形?
(九)探索发现
正三角形是中心对称图形吗?正方形呢?正五边形呢?正六边形呢?……你能发现什么规律?
边数为偶数的正多边形都是中心对称图形。
常见的轴对称图形和中心对称图形比较:
对图
称形
性
轴对称图形
中心对称图形
图形
对称轴条数
图形
对称中心
线段
角
等腰三角形
等边三角形
平行四边形
矩形
菱形
正方形
(十)小结
请大家先阅读课本最后一段话,然后结合本节课的学习谈谈你对中心对称图形有哪些认识?
四、教学反思
在教学过程中,应该鼓励学生进行自主探究,自己动手去探索中心对称图形的特点,加深对新知识的认识和理解.教师在课堂上起辅助作用,引导学生自己解决问题,注重培养学生的独立意识。
————中心对称图形
一、教学目标
1.知识与技能
(1)认识中心对称图形的有关概念;
(2)能判断某图形是不是中心对称图形.
2.过程与方法
经历观察、发现、探究中心对称图形的有关概念和基本性质,判断某图形是否是中心对称图形.
3.情感、态度与价值观
让学生体验到数学与生活的紧密联系;欣赏生活中的对称美,发展学生的美感
二、教学重难点
重点:中心对称图形的概念和性质.
难点:中心对称与中心对称图形的区别与联系.
三、教学活动设计
(一)知识回顾:
1、什么叫做中心对称?中心对称有哪些性质?
2、怎样作一个图形关于某一个定点的中心对称的图形?
3、已知任意四边形ABCD,请作出四边形ABCD关于点A的成中心对称的图形。
(二)情景引入
请认真观察下面两个动画,你发现它们有什么共同特征?
(三)总结新知
在平面内,如果一个图形绕一个点旋转180°后,能和原来的图形互相重合,那么这个图形叫做中心对称图形;这个点叫做它的对称中心;互相重合的点叫做对称点.
(四)探究
中心对称图形是旋转对称图形的一种特殊情形
(五)练习
判断下列图形是否是中心对称图形?如果是,那么对称中心在哪?
判定中心对称图形的方法:若图形上存在这样一个点,使整个图形绕着这个点旋转180°后能够与原来的图形重合,则这个图形就是中心对称图形。
下面的扑克牌中,哪些牌面是中心对称图形?
(六)思考
我们已经知道平行四边形是中心对称图形,现过对称中心任意画一直线将其分成两部分,这两部分面积有何关系?每一对对应点的连线有什么特点?
中心对称图形的性质:过对称中心的任意一条直线将中心对称图形分成面积相等的两部分;每一对对应点的连线都经过对称中心并且被对称中心平分。
(七)应用提升
张老汉有一块田地如图所示,他想田分给两个儿子,儿子提出:
⑴分割的面积应相等;
⑵最好把分割线做成一条水渠,便于灌溉。
你能帮助张老汉画出这条分割线吗?
(八)总结提升
1、中心对称与中心对称图形有什么区别与联系?
名称
中心对称
中心对称图形
定义
把一个图形绕着某一个点旋转180,如果他能够与另一个图形重合,那么就说这两个图形关于这点对称,这个点叫做对称中心,两个图形关于点对称也称中心对称
如果一个图形绕着一个点旋转180后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形
性质
①两个图形可完全重合;
②对应点连线都经过对称中心,并且被对称中心平分
③对应边平行或在同一条直线上
①对应点连线都经过对称中心,并且被对称中心平分
②过对称中心的任意一条直线将中心对称图形分成面积相等的两部分
区别
两个图形的位置关系
具有某种性质的一个图形
联系
若把中心对称图形的两部分分别看作两个图形,则它们成中心对称,若把中心对称的两个图形看作一个整体,则成为中心对称图形。
巩固应用
观察下面的几个图形哪些是中心对称?哪些是中心对称图形?
2、轴对称图形与中心对称图形有什么区别?
轴对称图形
中心对称图形
有一条对称轴——直线
有一个对称中心——点
图形沿轴对折
图形绕这个点旋转180O
对折部分与另一部分重合
旋转后与原图形重合
巩固练习
观察图形,并回答下面的问题:
(1)哪些只是轴对称图形?
(2)哪些只是中心对称图形?
(3)哪些既是轴对称图形,又是中心对称图形?
(九)探索发现
正三角形是中心对称图形吗?正方形呢?正五边形呢?正六边形呢?……你能发现什么规律?
边数为偶数的正多边形都是中心对称图形。
常见的轴对称图形和中心对称图形比较:
对图
称形
性
轴对称图形
中心对称图形
图形
对称轴条数
图形
对称中心
线段
角
等腰三角形
等边三角形
平行四边形
矩形
菱形
正方形
(十)小结
请大家先阅读课本最后一段话,然后结合本节课的学习谈谈你对中心对称图形有哪些认识?
四、教学反思
在教学过程中,应该鼓励学生进行自主探究,自己动手去探索中心对称图形的特点,加深对新知识的认识和理解.教师在课堂上起辅助作用,引导学生自己解决问题,注重培养学生的独立意识。
