人教版(五四制) 七年级数学下册 第17章 三角形 单元检测试题(Word版 含解析)
文档属性
| 名称 | 人教版(五四制) 七年级数学下册 第17章 三角形 单元检测试题(Word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 114.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-15 00:00:00 | ||
图片预览

文档简介
第17章
三角形
单元检测试题
(满分120分;时间:120分钟)
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
1.
如果一个三角形有两条高与其边重合,那么这个三角形是(
)三角形.
A.锐角
B.钝角
C.直角
D.不确定
?
2.
现有,,,长的四根木棒,任取其中三根组成一个三角形,那么可以组成的三角形的个数是(?
?
?
?
)
A.个
B.个
C.个
D.个
?
3.
若一个三角形有两条边相等,且有一内角为,那么这个三角形一定为(
)
A.钝角三角形
B.等腰三角形
C.直角三角形
D.正三角形
?
4.
人民币年版的一角硬币正面图案中有一个正九边形,如果设这个正九边形的半径为,那么它的周长是(
)
A.
B.
C.
D.
?
5.
如果一个多边形的每一个外角都是,那么这个多边形是(
)
A.四边形
B.五边形
C.六边形
D.八边形
?
6.
如图所示,,分别是的高和角平分线,且,,则的度数为(
)
A.
B.
C.
D.
?
7.
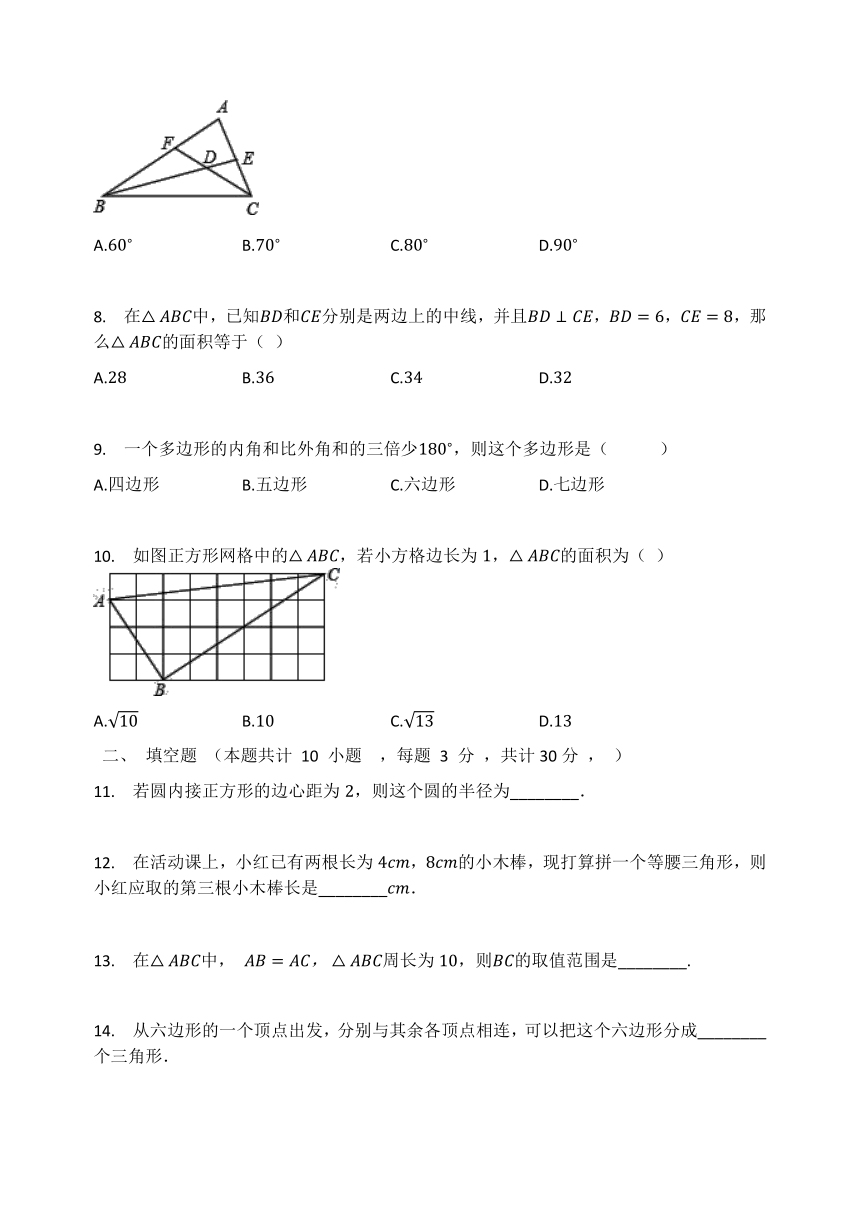
如图,、都是的角平分线,且,则的度数为(
)
A.
B.
C.
D.
?
8.
在中,已知和分别是两边上的中线,并且,,,那么的面积等于(
)
A.
B.
C.
D.
?
9.
一个多边形的内角和比外角和的三倍少,则这个多边形是(?
?
?
?
)
A.四边形
B.五边形
C.六边形
D.七边形
?
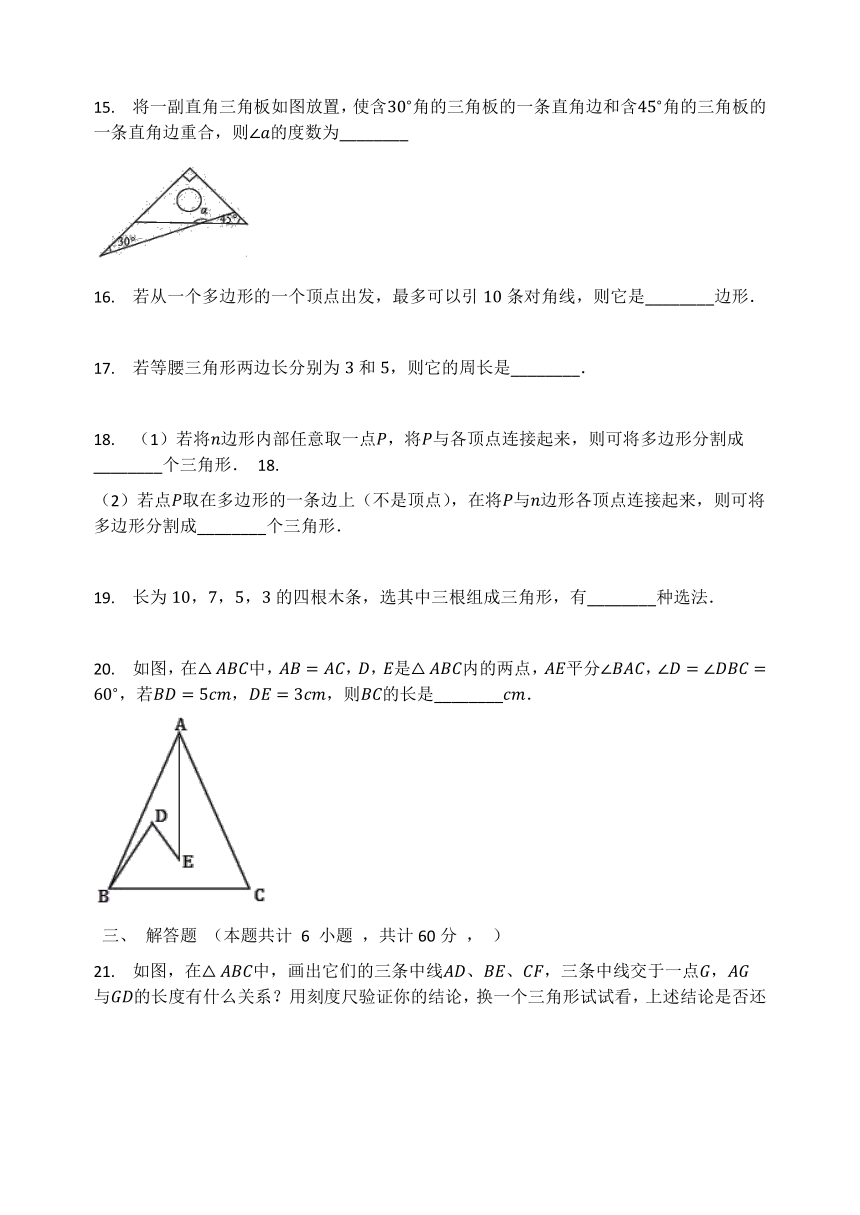
10.
如图正方形网格中的,若小方格边长为,的面积为(
)
A.
B.
C.
D.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?
11.
若圆内接正方形的边心距为,则这个圆的半径为________.
?
12.
在活动课上,小红已有两根长为,的小木棒,现打算拼一个等腰三角形,则小红应取的第三根小木棒长是________.
?
13.
在中,
?周长为,则的取值范围是________.
?
14.
从六边形的一个顶点出发,分别与其余各顶点相连,可以把这个六边形分成________个三角形.
?
15.
将一副直角三角板如图放置,使含角的三角板的一条直角边和含角的三角板的一条直角边重合,则的度数为________
?
16.
若从一个多边形的一个顶点出发,最多可以引条对角线,则它是________边形.
?
17.
若等腰三角形两边长分别为和,则它的周长是________.
?
18.
(1)若将边形内部任意取一点,将与各顶点连接起来,则可将多边形分割成________个三角形.
18.
(2)若点取在多边形的一条边上(不是顶点),在将与边形各顶点连接起来,则可将多边形分割成________个三角形.
?
19.
长为,,,的四根木条,选其中三根组成三角形,有________种选法.
?
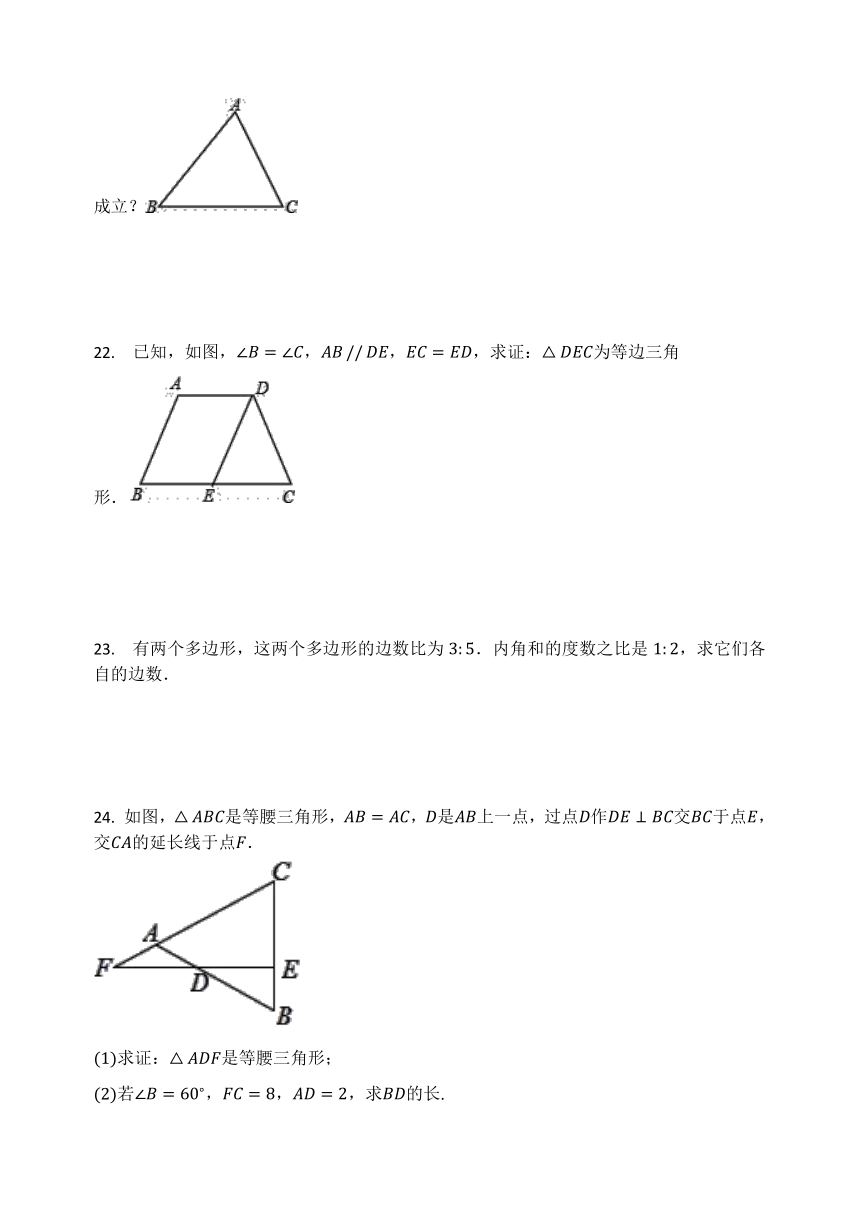
20.
如图,在中,,,是内的两点,平分,,若,,则的长是________.
三、
解答题
(本题共计
6
小题
,共计60分
,
)
?
21.
如图,在中,画出它们的三条中线、、,三条中线交于一点,与的长度有什么关系?用刻度尺验证你的结论,换一个三角形试试看,上述结论是否还成立?
?
22.
已知,如图,,,,求证:为等边三角形.
?
23.
有两个多边形,这两个多边形的边数比为.内角和的度数之比是,求它们各自的边数.
?
24.
如图,是等腰三角形,,是上一点,过点作交于点,交的延长线于点.
求证:是等腰三角形;
若,,,求的长.
?25.
如图,在中,点,在边,上,与相交于点,且=,=.
(1)求证:是等腰三角形;
(2)若=,=,求的度数.
?
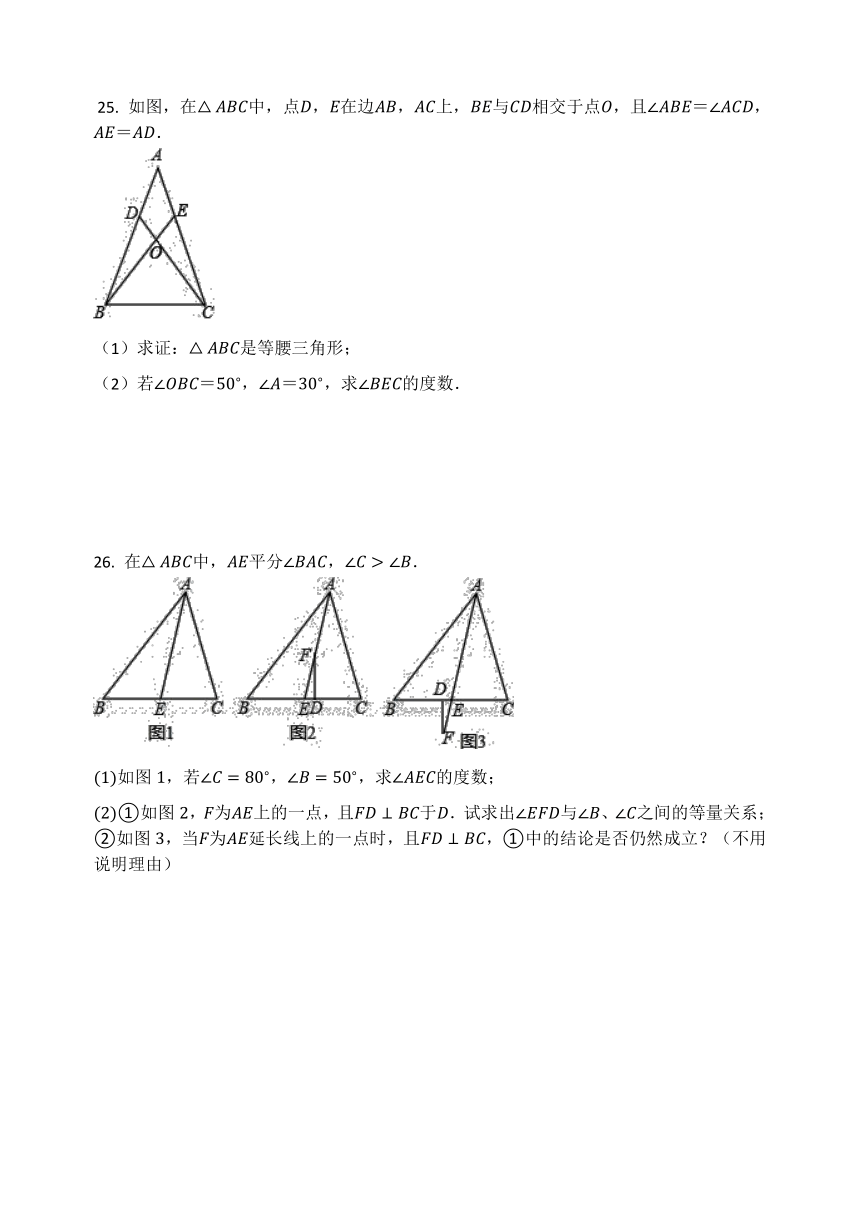
26.
在中,平分,.
如图,若,,求的度数;
①如图,为上的一点,且于.试求出与、之间的等量关系;
②如图,当为延长线上的一点时,且,①中的结论是否仍然成立?(不用说明理由)
参考答案
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
C
【解答】
解:一个三角形有两条高与其边重合,则这正是直角三角形的两个直角边,所以该三角形为直角三角形.
故选.
2.
【答案】
B
【解答】
解:四条木棒的所有组合:,,和,,和,,和,,;
只有,,和,,能组成三角形.
故选.
3.
【答案】
D
【解答】
解:根据有一个角是的等腰三角形是等边三角形可得到该三角形一定为正三角形.
故选.
4.
【答案】
C
【解答】
解:连接、,过作于,
则,
∵
九边形是正九边形,
∴
,,
在中,,
,
∵
,,
∴
,
即正九边形的周长是,
故选.
5.
【答案】
C
【解答】
解:.
故这个多边形是六边形.
故选.
6.
【答案】
A
【解答】
解:∵
,分别是的高和角平分线,且,,
∴
,,
∴
,
∴
.
故选.
7.
【答案】
C
【解答】
解:∵
、都是的角平分线,
∴
,
∵
,
∴
∴
,
∴
,
故选.
8.
【答案】
D
【解答】
解:连接,过点作,交的延长线于点.
∵
和分别是两边上的中线,
∴
,
∵
,,,
∴
,
∵
四边形为平行四边形,
∴
,
∴
,
∴
,
∵
,
∴
.
故选.
9.
【答案】
D
【解答】
解:设这个多边形的边数为,
由于多边形中边形的内角和等于,且任意多边形的外角和都为
根据题意可知,
解得
即这个多边形的边数是,
故选.
10.
【答案】
D
【解答】
解:的面积
.
故选.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
)
11.
【答案】
【解答】
解:过点作于点,
∵
圆内接正方形的边心距为,
∴
,,
∴
,
∴
这个圆的半径为:.
故答案为:.
12.
【答案】
【解答】
解:当第三根是时,其三边分别为,,,不符合三角形三边关系,故舍去;
当第三根是时,其三边分别是,,,符合三角形三边关系;
所以第三根长.
故答案为:.
13.
【答案】
【解答】
解:设,,根据题意,得.
再根据三角形的三边关系,得
解得.
∵
底边长为,
∴
,
∴
,
即.
故答案为:.
14.
【答案】
【解答】
解:当时,.
即可以把这个六边形分成了个三角形.
15.
【答案】
【解答】
解:如图,
由三角形的外角性质得,,
.
故答案为:.
16.
【答案】
【解答】
解:设这个多边形是边形.
依题意,得,
∴
.
故这个多边形是边形.
故答案为:.
17.
【答案】
或
【解答】
解:有两种情况:
①腰长为,底边长为,
三边为:,,可构成三角形,
周长;
②腰长为,底边长为,
三边为:,,可构成三角形,
周长.
故答案为:或.
18.
【答案】
解:(1)若将边形内部任意取一点,将与各顶点连接起来,则可将多边形分割成个三角形;
(2)若点取在多边形的一条边上(不是顶点),在将与边形各顶点连接起来,则可将多边形分割成个三角形.
【解答】
解:(1)若将边形内部任意取一点,将与各顶点连接起来,则可将多边形分割成个三角形;
(2)若点取在多边形的一条边上(不是顶点),在将与边形各顶点连接起来,则可将多边形分割成个三角形.
19.
【答案】
【解答】
解:每三根组合,有,,;,,;,,;,,四种情况.
根据三角形的三边关系,得其中的,,;,,不能组成三角形.
能够组成三角形的有种选法,它们分别是,,;,,.
故答案为:.
20.
【答案】
【解答】
解:延长交于,延长交于,如图所示,
∵
,平分,
∴
,.
∵
,
∴
为等边三角形,
∴
.
∵
,
∴
.
∵
为等边三角形,
∴
.
∵
,
∴
,
∴
,
∴
,
∴
,
∴
.
故答案为:.
三、
解答题
(本题共计
6
小题
,每题
10
分
,共计60分
)
21.
【答案】
解:,
换一个三角形,上述结论还成立,
证明:作交于,
∵
为的中点,
∴
为的中点,
∴
,又,
∴
.
【解答】
解:,
换一个三角形,上述结论还成立,
证明:作交于,
∵
为的中点,
∴
为的中点,
∴
,又,
∴
.
22.
【答案】
证明:∵
,,
∴
,
∵
,
∴
,
∴
,
∴
为等边三角形.
【解答】
证明:∵
,,
∴
,
∵
,
∴
,
∴
,
∴
为等边三角形.
23.
【答案】
解:∵
两个多边形的边数之比为,
∴
设多边形的边数为,则另一个为,
∵
内角和度数之比为,
∴
:,
解得:,,
∴
,.
故它们各自的边数为和.
【解答】
解:∵
两个多边形的边数之比为,
∴
设多边形的边数为,则另一个为,
∵
内角和度数之比为,
∴
:,
解得:,,
∴
,.
故它们各自的边数为和.
24.
【答案】
证明:∵
,
∴
,
∵
,
∴
,,
∴
,
而,
∴
,
∴
,
∴
是等腰三角形.
解:在
中,
,
是等边三角形
,
∴
,
∴
.
【解答】
证明:∵
,
∴
,
∵
,
∴
,,
∴
,
而,
∴
,
∴
,
∴
是等腰三角形.
解:在?中,
,
?是等边三角形
,
∴
,
∴
.
25.
【答案】
证明:在和中,,
∴
.
∴
=,
∴
是等腰三角形;
∵
=,
∴
====,
∴
===,
∴
的度数为.
【解答】
证明:在和中,,
∴
.
∴
=,
∴
是等腰三角形;
∵
=,
∴
====,
∴
===,
∴
的度数为.
26.
【答案】
解:∵
,,
∴
,
∵
平分,
∴
,
由三角形的外角性质得,
;
①由三角形的内角和定理得,
,
∵
平分,
∴
,
由三角形的外角性质得,
,
∵
,
∴
,
即;
②结论仍然成立.
【解答】
解:∵
,,
∴
,
∵
平分,
∴
,
由三角形的外角性质得,
;
①由三角形的内角和定理得,
,
∵
平分,
∴
,
由三角形的外角性质得,
,
∵
,
∴
,
即;
②结论仍然成立.
.
三角形
单元检测试题
(满分120分;时间:120分钟)
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
1.
如果一个三角形有两条高与其边重合,那么这个三角形是(
)三角形.
A.锐角
B.钝角
C.直角
D.不确定
?
2.
现有,,,长的四根木棒,任取其中三根组成一个三角形,那么可以组成的三角形的个数是(?
?
?
?
)
A.个
B.个
C.个
D.个
?
3.
若一个三角形有两条边相等,且有一内角为,那么这个三角形一定为(
)
A.钝角三角形
B.等腰三角形
C.直角三角形
D.正三角形
?
4.
人民币年版的一角硬币正面图案中有一个正九边形,如果设这个正九边形的半径为,那么它的周长是(
)
A.
B.
C.
D.
?
5.
如果一个多边形的每一个外角都是,那么这个多边形是(
)
A.四边形
B.五边形
C.六边形
D.八边形
?
6.
如图所示,,分别是的高和角平分线,且,,则的度数为(
)
A.
B.
C.
D.
?
7.
如图,、都是的角平分线,且,则的度数为(
)
A.
B.
C.
D.
?
8.
在中,已知和分别是两边上的中线,并且,,,那么的面积等于(
)
A.
B.
C.
D.
?
9.
一个多边形的内角和比外角和的三倍少,则这个多边形是(?
?
?
?
)
A.四边形
B.五边形
C.六边形
D.七边形
?
10.
如图正方形网格中的,若小方格边长为,的面积为(
)
A.
B.
C.
D.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?
11.
若圆内接正方形的边心距为,则这个圆的半径为________.
?
12.
在活动课上,小红已有两根长为,的小木棒,现打算拼一个等腰三角形,则小红应取的第三根小木棒长是________.
?
13.
在中,
?周长为,则的取值范围是________.
?
14.
从六边形的一个顶点出发,分别与其余各顶点相连,可以把这个六边形分成________个三角形.
?
15.
将一副直角三角板如图放置,使含角的三角板的一条直角边和含角的三角板的一条直角边重合,则的度数为________
?
16.
若从一个多边形的一个顶点出发,最多可以引条对角线,则它是________边形.
?
17.
若等腰三角形两边长分别为和,则它的周长是________.
?
18.
(1)若将边形内部任意取一点,将与各顶点连接起来,则可将多边形分割成________个三角形.
18.
(2)若点取在多边形的一条边上(不是顶点),在将与边形各顶点连接起来,则可将多边形分割成________个三角形.
?
19.
长为,,,的四根木条,选其中三根组成三角形,有________种选法.
?
20.
如图,在中,,,是内的两点,平分,,若,,则的长是________.
三、
解答题
(本题共计
6
小题
,共计60分
,
)
?
21.
如图,在中,画出它们的三条中线、、,三条中线交于一点,与的长度有什么关系?用刻度尺验证你的结论,换一个三角形试试看,上述结论是否还成立?
?
22.
已知,如图,,,,求证:为等边三角形.
?
23.
有两个多边形,这两个多边形的边数比为.内角和的度数之比是,求它们各自的边数.
?
24.
如图,是等腰三角形,,是上一点,过点作交于点,交的延长线于点.
求证:是等腰三角形;
若,,,求的长.
?25.
如图,在中,点,在边,上,与相交于点,且=,=.
(1)求证:是等腰三角形;
(2)若=,=,求的度数.
?
26.
在中,平分,.
如图,若,,求的度数;
①如图,为上的一点,且于.试求出与、之间的等量关系;
②如图,当为延长线上的一点时,且,①中的结论是否仍然成立?(不用说明理由)
参考答案
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
C
【解答】
解:一个三角形有两条高与其边重合,则这正是直角三角形的两个直角边,所以该三角形为直角三角形.
故选.
2.
【答案】
B
【解答】
解:四条木棒的所有组合:,,和,,和,,和,,;
只有,,和,,能组成三角形.
故选.
3.
【答案】
D
【解答】
解:根据有一个角是的等腰三角形是等边三角形可得到该三角形一定为正三角形.
故选.
4.
【答案】
C
【解答】
解:连接、,过作于,
则,
∵
九边形是正九边形,
∴
,,
在中,,
,
∵
,,
∴
,
即正九边形的周长是,
故选.
5.
【答案】
C
【解答】
解:.
故这个多边形是六边形.
故选.
6.
【答案】
A
【解答】
解:∵
,分别是的高和角平分线,且,,
∴
,,
∴
,
∴
.
故选.
7.
【答案】
C
【解答】
解:∵
、都是的角平分线,
∴
,
∵
,
∴
∴
,
∴
,
故选.
8.
【答案】
D
【解答】
解:连接,过点作,交的延长线于点.
∵
和分别是两边上的中线,
∴
,
∵
,,,
∴
,
∵
四边形为平行四边形,
∴
,
∴
,
∴
,
∵
,
∴
.
故选.
9.
【答案】
D
【解答】
解:设这个多边形的边数为,
由于多边形中边形的内角和等于,且任意多边形的外角和都为
根据题意可知,
解得
即这个多边形的边数是,
故选.
10.
【答案】
D
【解答】
解:的面积
.
故选.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
)
11.
【答案】
【解答】
解:过点作于点,
∵
圆内接正方形的边心距为,
∴
,,
∴
,
∴
这个圆的半径为:.
故答案为:.
12.
【答案】
【解答】
解:当第三根是时,其三边分别为,,,不符合三角形三边关系,故舍去;
当第三根是时,其三边分别是,,,符合三角形三边关系;
所以第三根长.
故答案为:.
13.
【答案】
【解答】
解:设,,根据题意,得.
再根据三角形的三边关系,得
解得.
∵
底边长为,
∴
,
∴
,
即.
故答案为:.
14.
【答案】
【解答】
解:当时,.
即可以把这个六边形分成了个三角形.
15.
【答案】
【解答】
解:如图,
由三角形的外角性质得,,
.
故答案为:.
16.
【答案】
【解答】
解:设这个多边形是边形.
依题意,得,
∴
.
故这个多边形是边形.
故答案为:.
17.
【答案】
或
【解答】
解:有两种情况:
①腰长为,底边长为,
三边为:,,可构成三角形,
周长;
②腰长为,底边长为,
三边为:,,可构成三角形,
周长.
故答案为:或.
18.
【答案】
解:(1)若将边形内部任意取一点,将与各顶点连接起来,则可将多边形分割成个三角形;
(2)若点取在多边形的一条边上(不是顶点),在将与边形各顶点连接起来,则可将多边形分割成个三角形.
【解答】
解:(1)若将边形内部任意取一点,将与各顶点连接起来,则可将多边形分割成个三角形;
(2)若点取在多边形的一条边上(不是顶点),在将与边形各顶点连接起来,则可将多边形分割成个三角形.
19.
【答案】
【解答】
解:每三根组合,有,,;,,;,,;,,四种情况.
根据三角形的三边关系,得其中的,,;,,不能组成三角形.
能够组成三角形的有种选法,它们分别是,,;,,.
故答案为:.
20.
【答案】
【解答】
解:延长交于,延长交于,如图所示,
∵
,平分,
∴
,.
∵
,
∴
为等边三角形,
∴
.
∵
,
∴
.
∵
为等边三角形,
∴
.
∵
,
∴
,
∴
,
∴
,
∴
,
∴
.
故答案为:.
三、
解答题
(本题共计
6
小题
,每题
10
分
,共计60分
)
21.
【答案】
解:,
换一个三角形,上述结论还成立,
证明:作交于,
∵
为的中点,
∴
为的中点,
∴
,又,
∴
.
【解答】
解:,
换一个三角形,上述结论还成立,
证明:作交于,
∵
为的中点,
∴
为的中点,
∴
,又,
∴
.
22.
【答案】
证明:∵
,,
∴
,
∵
,
∴
,
∴
,
∴
为等边三角形.
【解答】
证明:∵
,,
∴
,
∵
,
∴
,
∴
,
∴
为等边三角形.
23.
【答案】
解:∵
两个多边形的边数之比为,
∴
设多边形的边数为,则另一个为,
∵
内角和度数之比为,
∴
:,
解得:,,
∴
,.
故它们各自的边数为和.
【解答】
解:∵
两个多边形的边数之比为,
∴
设多边形的边数为,则另一个为,
∵
内角和度数之比为,
∴
:,
解得:,,
∴
,.
故它们各自的边数为和.
24.
【答案】
证明:∵
,
∴
,
∵
,
∴
,,
∴
,
而,
∴
,
∴
,
∴
是等腰三角形.
解:在
中,
,
是等边三角形
,
∴
,
∴
.
【解答】
证明:∵
,
∴
,
∵
,
∴
,,
∴
,
而,
∴
,
∴
,
∴
是等腰三角形.
解:在?中,
,
?是等边三角形
,
∴
,
∴
.
25.
【答案】
证明:在和中,,
∴
.
∴
=,
∴
是等腰三角形;
∵
=,
∴
====,
∴
===,
∴
的度数为.
【解答】
证明:在和中,,
∴
.
∴
=,
∴
是等腰三角形;
∵
=,
∴
====,
∴
===,
∴
的度数为.
26.
【答案】
解:∵
,,
∴
,
∵
平分,
∴
,
由三角形的外角性质得,
;
①由三角形的内角和定理得,
,
∵
平分,
∴
,
由三角形的外角性质得,
,
∵
,
∴
,
即;
②结论仍然成立.
【解答】
解:∵
,,
∴
,
∵
平分,
∴
,
由三角形的外角性质得,
;
①由三角形的内角和定理得,
,
∵
平分,
∴
,
由三角形的外角性质得,
,
∵
,
∴
,
即;
②结论仍然成立.
.
