人教版七年级数学上册同步检测4.3.3 余角和补角(word版含答案)
文档属性
| 名称 | 人教版七年级数学上册同步检测4.3.3 余角和补角(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 421.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-15 07:00:44 | ||
图片预览


文档简介
4.3.3
余角和补角
一、选择题(共11小题;共55分)
1.
如图,点
在直线
上,若
,则
的度数是
A.
B.
C.
D.
2.
如果
与
互为余角,则
A.
B.
C.
D.
3.
下面角的图示中,能与
角互补的是
A.
B.
C.
D.
4.
下列叙述正确的是
A.
的角是补角
B.
和
的角互为补角
C.
,,
的角互为补角
D.
和
的角互为补角
5.
如图,直线
,
交于点
,因为
,,所以
的依据是
A.
同角的余角相等
B.
等角的余角相等
C.
同角的补角相等
D.
等角的补角相等
6.
若
与
互补,
与
互补,,则
等于
A.
B.
C.
D.
7.
如果
,又
与
互余,那么
与
的关系是
A.
互余
B.
互补
C.
相等
D.
不能确定
8.
如图所示,点
在点
的
A.
北偏东
方向
B.
南偏东
方向
C.
南偏西
方向
D.
南偏西
方向
9.
如图,下面说法中不正确的是
A.
射线
表示北偏东
B.
射线
表示西北方向
C.
射线
表示西偏南
D.
射线
表示南偏东
10.
如图,,则
与
的关系是
A.
互余
B.
互补
C.
相等
D.
法确定
11.
一个角的补角比它的余角
A.
相等
B.
小
C.
大
D.
不确定大小
二、填空题(共4小题;共20分)
12.
已知
,则
的余角大小是
?.
13.
互为余角且相等的角的度数都是
?,互为补角且相等的角的度数都是
?.
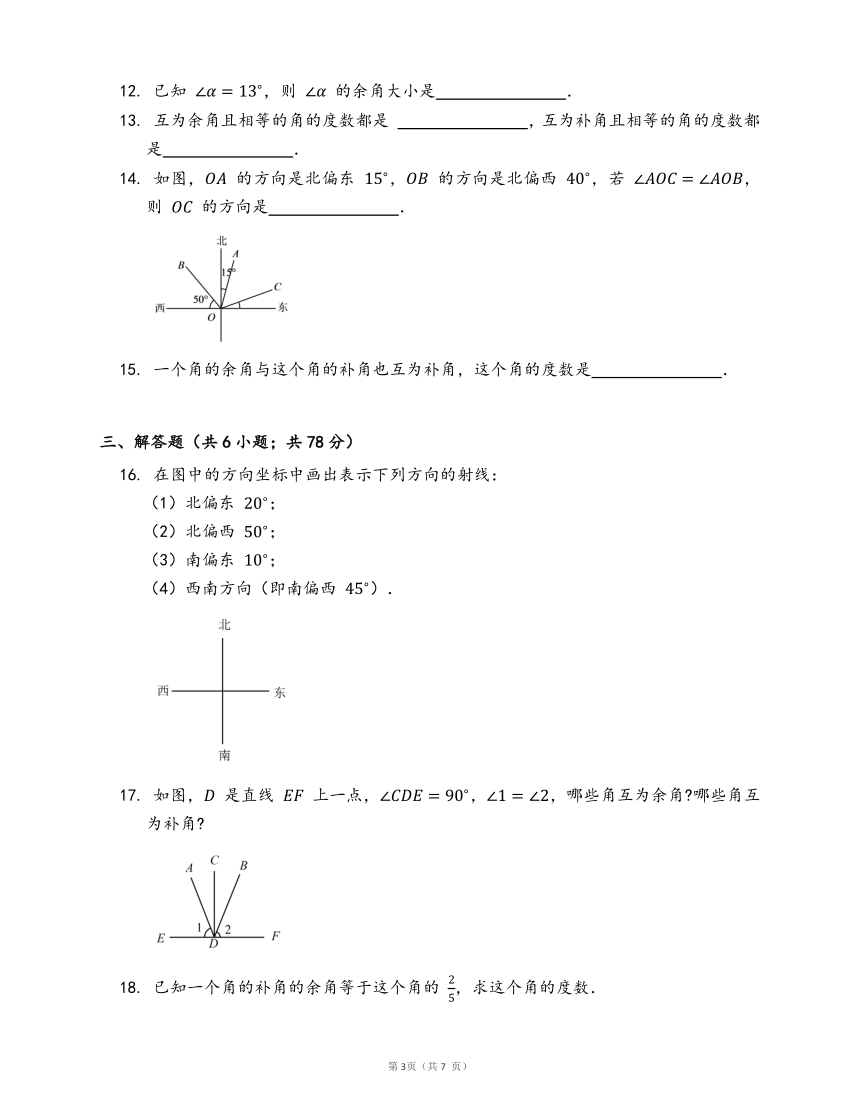
14.
如图,
的方向是北偏东
,
的方向是北偏西
,若
,则
的方向是
?.
15.
一个角的余角与这个角的补角也互为补角,这个角的度数是
?.
三、解答题(共6小题;共78分)
16.
在图中的方向坐标中画出表示下列方向的射线:
(1)北偏东
;
(2)北偏西
;
(3)南偏东
;
(4)西南方向(即南偏西
).
17.
如图,
是直线
上一点,,,哪些角互为余角?哪些角互为补角?
18.
已知一个角的补角的余角等于这个角的
,求这个角的度数.
19.
如图,
平分
,
平分
,若
,,请求出
与
的大小,并判断它们是否互补.
20.
如图,
是直线
上一点,
为任一条射线,
平分
,
平分
.
(1)指出图中
与
的补角;
(2)试说明
与
具有怎样的数量关系.
21.
如图,先找到长方形纸的宽
的中点
,将
过
点折起任意一个角,折痕是
,再将
过
点折起,使
和
重合,折痕是
,请探索下列问题:
(1)
和
互为余角吗?为什么?
(2)在上述折纸图形中,还有哪些角互为余角?
答案
第一部分
1.
C
【解析】根据邻补角的定义可知
,
所以
.
2.
D
3.
D
4.
D
5.
C
6.
A
7.
C
8.
A
9.
C
10.
B
11.
C
第二部分
12.
13.
,
14.
北偏东
15.
第三部分
16.
如图.
17.
与
,
与
,
与
,
与
互为余角;
与
,
与
,
与
,
与
,
与
互为补角.
18.
这个角为
,
根据题意,得
解得
答:这个角为
.
19.
因为
平分
,,
.
因为
平分
,,
所以
,
所以
.
因为
,,
所以
,
所以
.
所以
与
互补.
20.
(1)
与
互补的角是
,;
与
互补的角是
,.
??????(2)
.
理由如下:
因为
平分
,
平分
,
所以
,,
所以
.
21.
(1)
和
互为余角.
理由:
由折纸试验,知
,,
而
,
所以
,即
,
故
和
互为余角.
??????(2)
互余的角还有:
与
,
与
,
与
,
与
,
与
,
与
,
与
,
与
,
与
,
与
,
与
.
第5页(共7
页)
余角和补角
一、选择题(共11小题;共55分)
1.
如图,点
在直线
上,若
,则
的度数是
A.
B.
C.
D.
2.
如果
与
互为余角,则
A.
B.
C.
D.
3.
下面角的图示中,能与
角互补的是
A.
B.
C.
D.
4.
下列叙述正确的是
A.
的角是补角
B.
和
的角互为补角
C.
,,
的角互为补角
D.
和
的角互为补角
5.
如图,直线
,
交于点
,因为
,,所以
的依据是
A.
同角的余角相等
B.
等角的余角相等
C.
同角的补角相等
D.
等角的补角相等
6.
若
与
互补,
与
互补,,则
等于
A.
B.
C.
D.
7.
如果
,又
与
互余,那么
与
的关系是
A.
互余
B.
互补
C.
相等
D.
不能确定
8.
如图所示,点
在点
的
A.
北偏东
方向
B.
南偏东
方向
C.
南偏西
方向
D.
南偏西
方向
9.
如图,下面说法中不正确的是
A.
射线
表示北偏东
B.
射线
表示西北方向
C.
射线
表示西偏南
D.
射线
表示南偏东
10.
如图,,则
与
的关系是
A.
互余
B.
互补
C.
相等
D.
法确定
11.
一个角的补角比它的余角
A.
相等
B.
小
C.
大
D.
不确定大小
二、填空题(共4小题;共20分)
12.
已知
,则
的余角大小是
?.
13.
互为余角且相等的角的度数都是
?,互为补角且相等的角的度数都是
?.
14.
如图,
的方向是北偏东
,
的方向是北偏西
,若
,则
的方向是
?.
15.
一个角的余角与这个角的补角也互为补角,这个角的度数是
?.
三、解答题(共6小题;共78分)
16.
在图中的方向坐标中画出表示下列方向的射线:
(1)北偏东
;
(2)北偏西
;
(3)南偏东
;
(4)西南方向(即南偏西
).
17.
如图,
是直线
上一点,,,哪些角互为余角?哪些角互为补角?
18.
已知一个角的补角的余角等于这个角的
,求这个角的度数.
19.
如图,
平分
,
平分
,若
,,请求出
与
的大小,并判断它们是否互补.
20.
如图,
是直线
上一点,
为任一条射线,
平分
,
平分
.
(1)指出图中
与
的补角;
(2)试说明
与
具有怎样的数量关系.
21.
如图,先找到长方形纸的宽
的中点
,将
过
点折起任意一个角,折痕是
,再将
过
点折起,使
和
重合,折痕是
,请探索下列问题:
(1)
和
互为余角吗?为什么?
(2)在上述折纸图形中,还有哪些角互为余角?
答案
第一部分
1.
C
【解析】根据邻补角的定义可知
,
所以
.
2.
D
3.
D
4.
D
5.
C
6.
A
7.
C
8.
A
9.
C
10.
B
11.
C
第二部分
12.
13.
,
14.
北偏东
15.
第三部分
16.
如图.
17.
与
,
与
,
与
,
与
互为余角;
与
,
与
,
与
,
与
,
与
互为补角.
18.
这个角为
,
根据题意,得
解得
答:这个角为
.
19.
因为
平分
,,
.
因为
平分
,,
所以
,
所以
.
因为
,,
所以
,
所以
.
所以
与
互补.
20.
(1)
与
互补的角是
,;
与
互补的角是
,.
??????(2)
.
理由如下:
因为
平分
,
平分
,
所以
,,
所以
.
21.
(1)
和
互为余角.
理由:
由折纸试验,知
,,
而
,
所以
,即
,
故
和
互为余角.
??????(2)
互余的角还有:
与
,
与
,
与
,
与
,
与
,
与
,
与
,
与
,
与
,
与
,
与
.
第5页(共7
页)
