人教版数学八年级上册 第12章 12.1全等三角形 同步测试题(一)(word版含答案)
文档属性
| 名称 | 人教版数学八年级上册 第12章 12.1全等三角形 同步测试题(一)(word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 132.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-15 07:02:14 | ||
图片预览


文档简介
全等三角形同步测试题(一)
一.选择题
1.已知△ABC≌△A1B1C1,若∠C=60°,则∠C1的度数为( )
A.50°
B.60°
C.70°
D.120°
2.下列各组中的两个图形属于全等图形的是( )
A.
B.
C.
D.
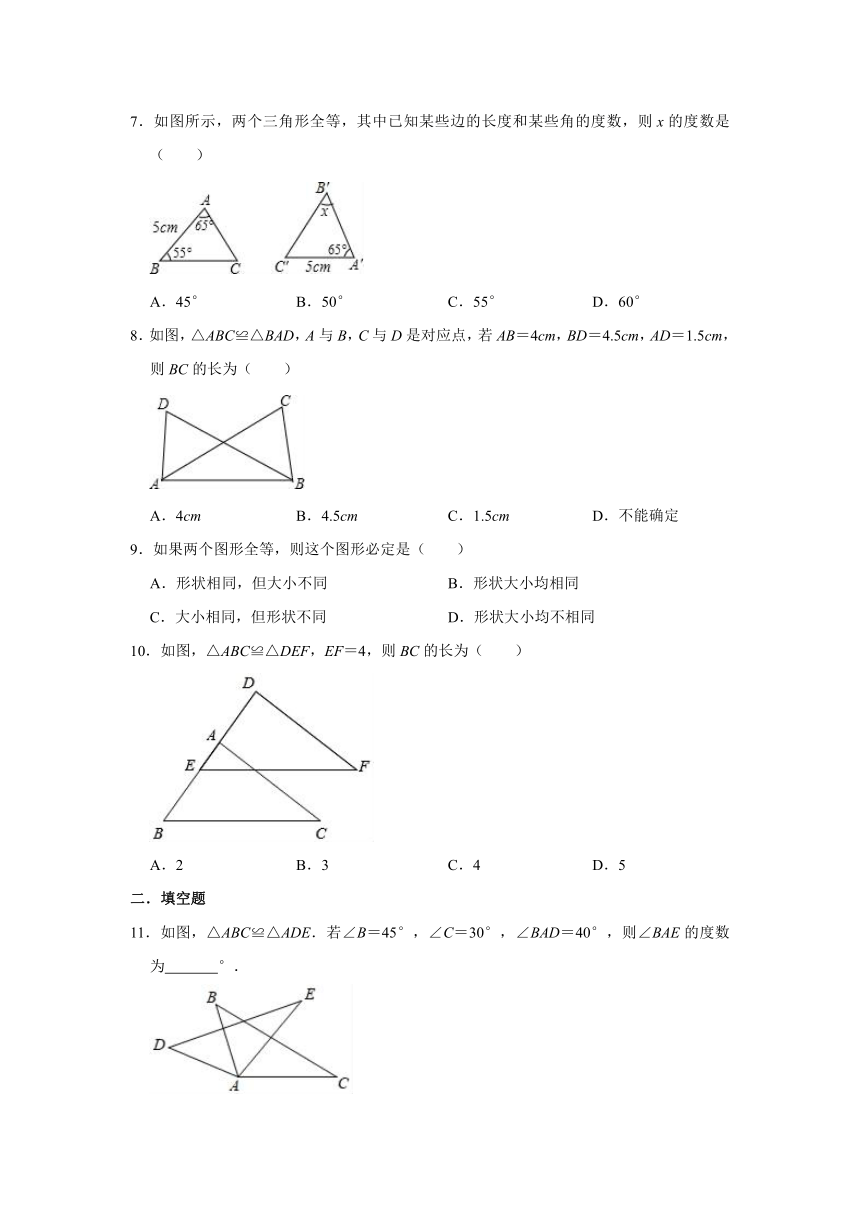
3.如图,△ABD≌△CDB,下面四个结论中,不正确的是( )
A.∠ABD=∠CBD
B.△ABD和△CDB的周长相等
C.AD=BC
D.△ABD和△CDB的面积相等
4.如图,△ABN≌△ACM,AB=AC,BN=CM,∠B=50°,∠ANC=120°,则∠MAC的度数等于( )
A.120°
B.70°
C.60°
D.50°
5.下列判断正确的个数是( )
(1)能够完全重合的两个图形全等;
(2)两边和一角对应相等的两个三角形全等;
(3)两角和一边对应相等的两个三角形全等;
(4)全等三角形对应边相等.
A.1个
B.2个
C.3个
D.4个
6.若△ABC≌△DEF,∠A=80°,∠B=40°,那么∠F的度数是( )
A.80°
B.40°
C.60°
D.120°
7.如图所示,两个三角形全等,其中已知某些边的长度和某些角的度数,则x的度数是( )
A.45°
B.50°
C.55°
D.60°
8.如图,△ABC≌△BAD,A与B,C与D是对应点,若AB=4cm,BD=4.5cm,AD=1.5cm,则BC的长为( )
A.4cm
B.4.5cm
C.1.5cm
D.不能确定
9.如果两个图形全等,则这个图形必定是( )
A.形状相同,但大小不同
B.形状大小均相同
C.大小相同,但形状不同
D.形状大小均不相同
10.如图,△ABC≌△DEF,EF=4,则BC的长为( )
A.2
B.3
C.4
D.5
二.填空题
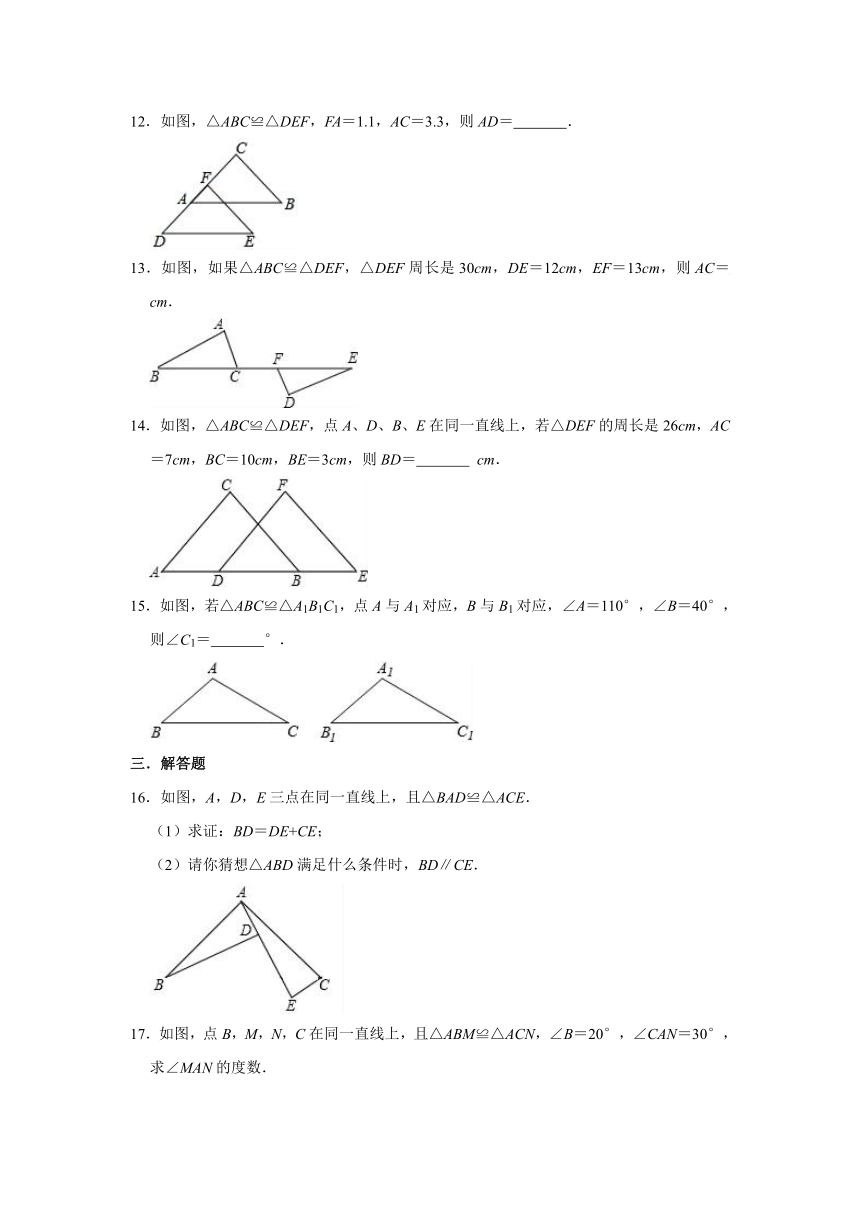
11.如图,△ABC≌△ADE.若∠B=45°,∠C=30°,∠BAD=40°,则∠BAE的度数为
°.
12.如图,△ABC≌△DEF,FA=1.1,AC=3.3,则AD=
.
13.如图,如果△ABC≌△DEF,△DEF周长是30cm,DE=12cm,EF=13cm,则AC=
cm.
14.如图,△ABC≌△DEF,点A、D、B、E在同一直线上,若△DEF的周长是26cm,AC=7cm,BC=10cm,BE=3cm,则BD=
cm.
15.如图,若△ABC≌△A1B1C1,点A与A1对应,B与B1对应,∠A=110°,∠B=40°,则∠C1=
°.
三.解答题
16.如图,A,D,E三点在同一直线上,且△BAD≌△ACE.
(1)求证:BD=DE+CE;
(2)请你猜想△ABD满足什么条件时,BD∥CE.
17.如图,点B,M,N,C在同一直线上,且△ABM≌△ACN,∠B=20°,∠CAN=30°,求∠MAN的度数.
18.如图,指出图中的全等图形.
19.国昌实验中学八年级合作学习小组的同学学习了全等三角形的概念后,聪明的正宇同学代表本小组给其他小组内的同学出了这样一个问题:在直角坐标系中,点A(﹣3,0),B(﹣1,0),C(﹣1,3),若有一个直角三角形与Rt△ABC全等,且它们只有一条公共直角边.这样的直角三角形有几个?若有,请写出第三个顶点的坐标.
参考答案与试题解析
一.选择题
1.【解答】解:∵△ABC≌△A1B1C1,
∴∠C1=∠C=60°,
故选:B.
2.【解答】解:A、两个图形不属于全等图形,故此选项不合题意;
B、两个图形不属于全等图形,故此选项不合题意;
C、两个图形不属于全等图形,故此选项不合题意;
D、两个图形属于全等图形,故此选项符合题意;
故选:D.
3.【解答】解:A、∵△ABD≌△CDB,∴∠ABD=∠CDB,选项说法错误;
B、∵△ABD≌△CDB,
∴△ABD和△CDB的周长相等,选项说法正确;
C、∵△ABD≌△CDB,∴AD=BC,选项说法正确;
D、∵△ABD≌△CDB,
∴△ABD和△CDB的面积相等,选项说法正确;
故选:A.
4.【解答】解:∵∠ANC=120°,
∴∠ANB=180°﹣120°=60°,
∵∠B=50°,
∴∠BAN=180°﹣60°﹣50°=70°,
∵△ABN≌△ACM,
∴∠BAN=∠MAC=70°.
故选:B.
5.【解答】解:(1)能够完全重合的两个图形全等,正确;
(2)两边和一角对应相等的两个三角形全等,必须是SAS才可以得出全等,错误;
(3)根据“ASA”或“AAS”定理,有两角和一边对应相等的两个三角形,比如一边是两角的夹边和一角对边相等,则这两个三角形就不全等,故原说法错误;
(4)全等三角形对应边相等,正确.
所以有2个判断正确.
故选:B.
6.【解答】解:∵∠A=80°,∠B=40°,
∴∠C=180°﹣∠A﹣∠B=60°,
∵△ABC≌△DEF,
∴∠F=∠C=60°,
故选:C.
7.【解答】解:△ABC中,∠A=65°,∠B=55°,
∴∠C=180°﹣∠A﹣∠B=60°,
∵两个三角形全等,
又∵∠A=∠A′=65°,AB=A′C′=5cm
∴点C的对应点是B′,
∴x=∠B′=∠C=60°.
故选:D.
8.【解答】解:∵△ABC≌△BAD,A与B,C与D是对应点,
∴BC=AD.
又∵AD=1.5cm,
∴BC=1.5cm.
故选:C.
9.【解答】解:如果两个图形全等,则这个图形必定是形状大小完全相同.
故选:B.
10.【解答】解:∵△ABC≌△DEF,EF=4,
∴BC=EF=4,
故选:C.
二.填空题(共5小题)
11.【解答】解:∵△ABC≌△ADE,
∴∠B=∠D=45°,∠C=∠E=30°,
∴∠DAE=180°﹣45°﹣30°=105°.
∵∠BAD=40°,
∴∠BAE=105°﹣40°=65°.
故答案为:65.
12.【解答】解:∵△ABC≌△DEF,
∴AC=DF,
∴AD=FC,
∵FA=1.1,AC=3.3,
∴AD=FC=AC﹣FA=3.3﹣1.1=2.2,
故答案为:2.2.
13.【解答】解:
∵△DEF周长是30cm,DE=12cm,EF=13cm,
∴DF=5cm,
∵△ABC≌△DEF,
∴AC=DF=5cm,
故答案为:5.
14.【解答】解:∵△ABC≌△DEF,
∴AB=DE,AC=FD,BC=EF.
∴DE=26﹣7﹣10=9.
∴BD=DE﹣BE=9﹣3=6cm.
故答案为:6.
15.【解答】解:∵△ABC≌△A1B1C1,
∴∠C1=∠C,
又∵∠C=180°﹣∠A﹣∠B=180°﹣110°﹣40°=30°,
∴∠C1=∠C=30°.
故答案为:30.
三.解答题(共4小题)
16.【解答】(1)证明:∵△BAD≌△ACE,
∴AD=CE,BD=AE,
∵A,D,E三点在同一直线上,
∴AE=AD+DE,
∴BD=CE+DE;
(2)解:假如BD∥CE,
则∠BDE=∠E,
∵△BAD≌△ACE,
∴∠ADB=∠E,
∴∠ADB=∠BDE,
又∵∠ADB+∠BDE=180°,
∴∠ADB=∠BDE=90°,
∴当∠ADB=∠E=90°时,BD∥CE.
17.【解答】解:∵△ABM≌△ACN,∠B=20°,∠CAN=30°,
∴∠BAM=∠CAN=30°,AM=AN,
∴∠AMN=30°+20°=50°,
∴∠ANM=∠AMN=50°,
∴∠MAN=180°﹣50°﹣50°=80°.
18.【解答】解:⑤和⑨是全等形;
故答案为:⑤和⑨.
19.【解答】解:如图:与Rt△ABC全等,且它们只有一条公共直角边的三角形有:
△ABD、△ABE、△BCF、△BCE、△BCG、△ABH共6个.
第三个顶点点D的坐标(﹣1,﹣3)
点E的坐标(﹣3,3),
点F的坐标(1,0),
点G的坐标(1,3),
点H的坐标(﹣3,﹣3).
一.选择题
1.已知△ABC≌△A1B1C1,若∠C=60°,则∠C1的度数为( )
A.50°
B.60°
C.70°
D.120°
2.下列各组中的两个图形属于全等图形的是( )
A.
B.
C.
D.
3.如图,△ABD≌△CDB,下面四个结论中,不正确的是( )
A.∠ABD=∠CBD
B.△ABD和△CDB的周长相等
C.AD=BC
D.△ABD和△CDB的面积相等
4.如图,△ABN≌△ACM,AB=AC,BN=CM,∠B=50°,∠ANC=120°,则∠MAC的度数等于( )
A.120°
B.70°
C.60°
D.50°
5.下列判断正确的个数是( )
(1)能够完全重合的两个图形全等;
(2)两边和一角对应相等的两个三角形全等;
(3)两角和一边对应相等的两个三角形全等;
(4)全等三角形对应边相等.
A.1个
B.2个
C.3个
D.4个
6.若△ABC≌△DEF,∠A=80°,∠B=40°,那么∠F的度数是( )
A.80°
B.40°
C.60°
D.120°
7.如图所示,两个三角形全等,其中已知某些边的长度和某些角的度数,则x的度数是( )
A.45°
B.50°
C.55°
D.60°
8.如图,△ABC≌△BAD,A与B,C与D是对应点,若AB=4cm,BD=4.5cm,AD=1.5cm,则BC的长为( )
A.4cm
B.4.5cm
C.1.5cm
D.不能确定
9.如果两个图形全等,则这个图形必定是( )
A.形状相同,但大小不同
B.形状大小均相同
C.大小相同,但形状不同
D.形状大小均不相同
10.如图,△ABC≌△DEF,EF=4,则BC的长为( )
A.2
B.3
C.4
D.5
二.填空题
11.如图,△ABC≌△ADE.若∠B=45°,∠C=30°,∠BAD=40°,则∠BAE的度数为
°.
12.如图,△ABC≌△DEF,FA=1.1,AC=3.3,则AD=
.
13.如图,如果△ABC≌△DEF,△DEF周长是30cm,DE=12cm,EF=13cm,则AC=
cm.
14.如图,△ABC≌△DEF,点A、D、B、E在同一直线上,若△DEF的周长是26cm,AC=7cm,BC=10cm,BE=3cm,则BD=
cm.
15.如图,若△ABC≌△A1B1C1,点A与A1对应,B与B1对应,∠A=110°,∠B=40°,则∠C1=
°.
三.解答题
16.如图,A,D,E三点在同一直线上,且△BAD≌△ACE.
(1)求证:BD=DE+CE;
(2)请你猜想△ABD满足什么条件时,BD∥CE.
17.如图,点B,M,N,C在同一直线上,且△ABM≌△ACN,∠B=20°,∠CAN=30°,求∠MAN的度数.
18.如图,指出图中的全等图形.
19.国昌实验中学八年级合作学习小组的同学学习了全等三角形的概念后,聪明的正宇同学代表本小组给其他小组内的同学出了这样一个问题:在直角坐标系中,点A(﹣3,0),B(﹣1,0),C(﹣1,3),若有一个直角三角形与Rt△ABC全等,且它们只有一条公共直角边.这样的直角三角形有几个?若有,请写出第三个顶点的坐标.
参考答案与试题解析
一.选择题
1.【解答】解:∵△ABC≌△A1B1C1,
∴∠C1=∠C=60°,
故选:B.
2.【解答】解:A、两个图形不属于全等图形,故此选项不合题意;
B、两个图形不属于全等图形,故此选项不合题意;
C、两个图形不属于全等图形,故此选项不合题意;
D、两个图形属于全等图形,故此选项符合题意;
故选:D.
3.【解答】解:A、∵△ABD≌△CDB,∴∠ABD=∠CDB,选项说法错误;
B、∵△ABD≌△CDB,
∴△ABD和△CDB的周长相等,选项说法正确;
C、∵△ABD≌△CDB,∴AD=BC,选项说法正确;
D、∵△ABD≌△CDB,
∴△ABD和△CDB的面积相等,选项说法正确;
故选:A.
4.【解答】解:∵∠ANC=120°,
∴∠ANB=180°﹣120°=60°,
∵∠B=50°,
∴∠BAN=180°﹣60°﹣50°=70°,
∵△ABN≌△ACM,
∴∠BAN=∠MAC=70°.
故选:B.
5.【解答】解:(1)能够完全重合的两个图形全等,正确;
(2)两边和一角对应相等的两个三角形全等,必须是SAS才可以得出全等,错误;
(3)根据“ASA”或“AAS”定理,有两角和一边对应相等的两个三角形,比如一边是两角的夹边和一角对边相等,则这两个三角形就不全等,故原说法错误;
(4)全等三角形对应边相等,正确.
所以有2个判断正确.
故选:B.
6.【解答】解:∵∠A=80°,∠B=40°,
∴∠C=180°﹣∠A﹣∠B=60°,
∵△ABC≌△DEF,
∴∠F=∠C=60°,
故选:C.
7.【解答】解:△ABC中,∠A=65°,∠B=55°,
∴∠C=180°﹣∠A﹣∠B=60°,
∵两个三角形全等,
又∵∠A=∠A′=65°,AB=A′C′=5cm
∴点C的对应点是B′,
∴x=∠B′=∠C=60°.
故选:D.
8.【解答】解:∵△ABC≌△BAD,A与B,C与D是对应点,
∴BC=AD.
又∵AD=1.5cm,
∴BC=1.5cm.
故选:C.
9.【解答】解:如果两个图形全等,则这个图形必定是形状大小完全相同.
故选:B.
10.【解答】解:∵△ABC≌△DEF,EF=4,
∴BC=EF=4,
故选:C.
二.填空题(共5小题)
11.【解答】解:∵△ABC≌△ADE,
∴∠B=∠D=45°,∠C=∠E=30°,
∴∠DAE=180°﹣45°﹣30°=105°.
∵∠BAD=40°,
∴∠BAE=105°﹣40°=65°.
故答案为:65.
12.【解答】解:∵△ABC≌△DEF,
∴AC=DF,
∴AD=FC,
∵FA=1.1,AC=3.3,
∴AD=FC=AC﹣FA=3.3﹣1.1=2.2,
故答案为:2.2.
13.【解答】解:
∵△DEF周长是30cm,DE=12cm,EF=13cm,
∴DF=5cm,
∵△ABC≌△DEF,
∴AC=DF=5cm,
故答案为:5.
14.【解答】解:∵△ABC≌△DEF,
∴AB=DE,AC=FD,BC=EF.
∴DE=26﹣7﹣10=9.
∴BD=DE﹣BE=9﹣3=6cm.
故答案为:6.
15.【解答】解:∵△ABC≌△A1B1C1,
∴∠C1=∠C,
又∵∠C=180°﹣∠A﹣∠B=180°﹣110°﹣40°=30°,
∴∠C1=∠C=30°.
故答案为:30.
三.解答题(共4小题)
16.【解答】(1)证明:∵△BAD≌△ACE,
∴AD=CE,BD=AE,
∵A,D,E三点在同一直线上,
∴AE=AD+DE,
∴BD=CE+DE;
(2)解:假如BD∥CE,
则∠BDE=∠E,
∵△BAD≌△ACE,
∴∠ADB=∠E,
∴∠ADB=∠BDE,
又∵∠ADB+∠BDE=180°,
∴∠ADB=∠BDE=90°,
∴当∠ADB=∠E=90°时,BD∥CE.
17.【解答】解:∵△ABM≌△ACN,∠B=20°,∠CAN=30°,
∴∠BAM=∠CAN=30°,AM=AN,
∴∠AMN=30°+20°=50°,
∴∠ANM=∠AMN=50°,
∴∠MAN=180°﹣50°﹣50°=80°.
18.【解答】解:⑤和⑨是全等形;
故答案为:⑤和⑨.
19.【解答】解:如图:与Rt△ABC全等,且它们只有一条公共直角边的三角形有:
△ABD、△ABE、△BCF、△BCE、△BCG、△ABH共6个.
第三个顶点点D的坐标(﹣1,﹣3)
点E的坐标(﹣3,3),
点F的坐标(1,0),
点G的坐标(1,3),
点H的坐标(﹣3,﹣3).
