人教版数学八年级下册 第19章 19.1函数同步测试试题(word解析版)
文档属性
| 名称 | 人教版数学八年级下册 第19章 19.1函数同步测试试题(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 295.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-15 07:13:21 | ||
图片预览

文档简介
函数同步测试试题(一)
一.选择题
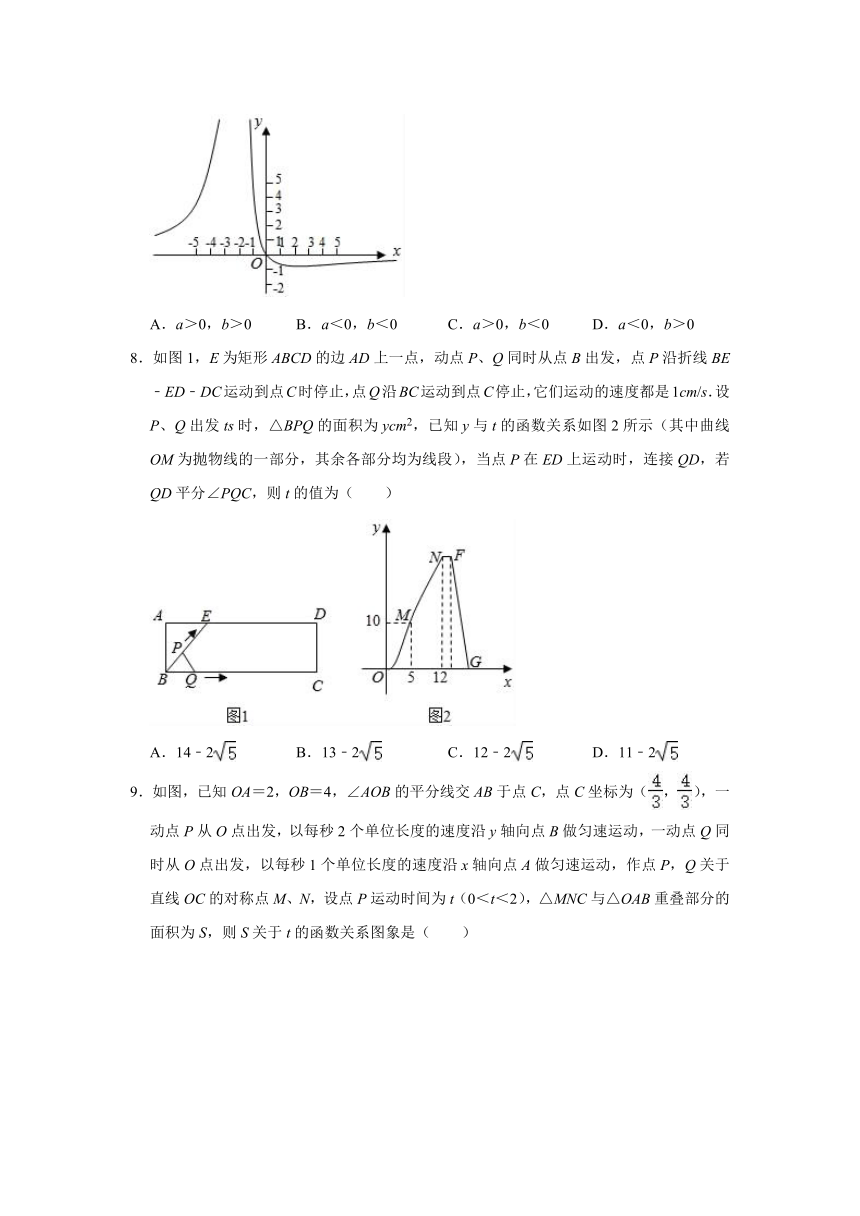
1.如果每盒笔售价16元,共有10支,用y(元)表示笔的售价,x表示笔的支数,那么y与x的关系式为( )
A.y=10x
B.y=16x
C.y=x
D.y=x
2.根据如图所示的计算程序,若输入x=﹣2,则输出结果y的值为( )
A.﹣3
B.3
C.﹣7
D.7
3.函数y=自变量x的取值范围是( )
A.x≠3
B.x≤5
C.x≤5且x≠3
D.x<5且x≠3
4.函数y=自变量的取值范围是( )
A.x≠2020
B.x≠﹣2020
C.x≠2021
D.x≠﹣2021
5.下列图形中,不能代表y是x函数的是( )
A.
B.
C.
D.
6.函数y=中自变量x的取值范围是( )
A.x≥2
B.x≥2且x≠﹣1
C.x>2且x≠﹣1
D.x≠﹣1
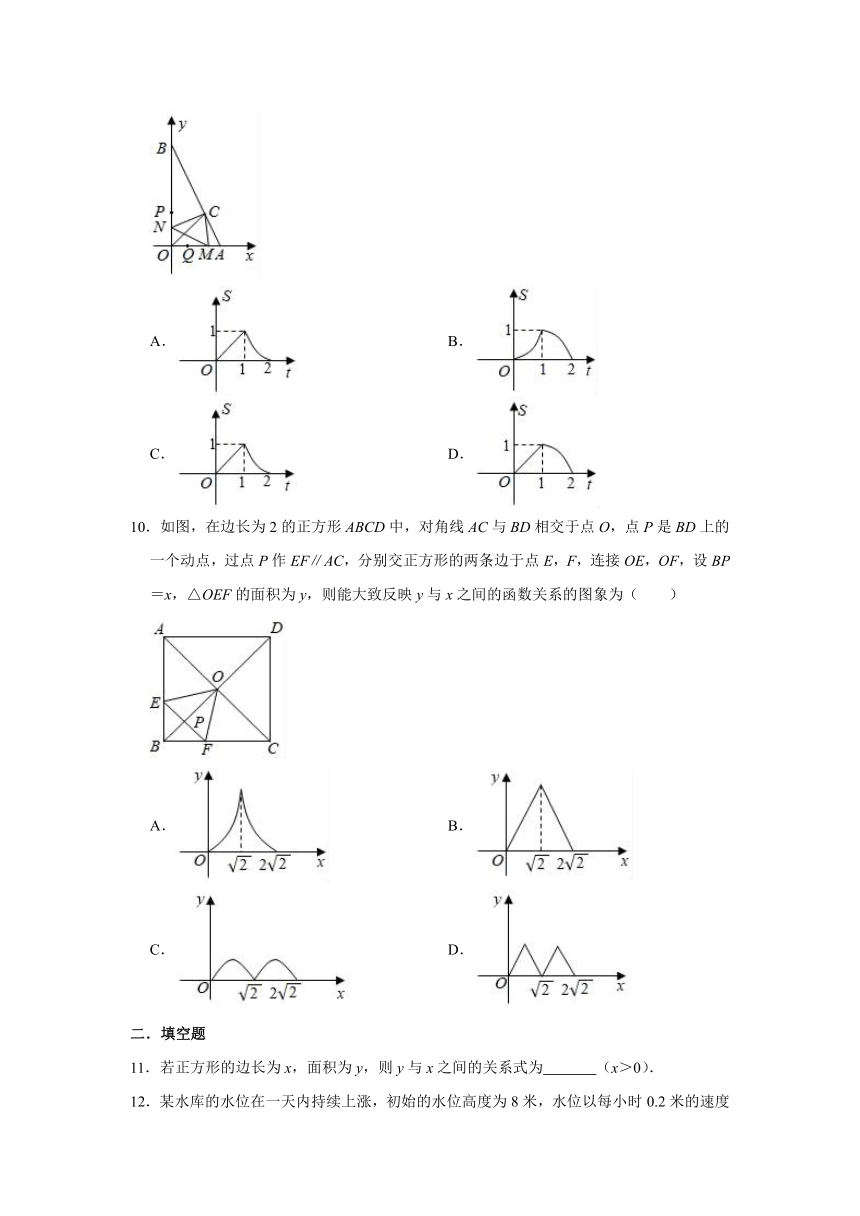
7.已知关于x的函数的图象如图所示,根据探究函数图象的经验,可以推断常数a,b的值满足( )
A.a>0,b>0
B.a<0,b<0
C.a>0,b<0
D.a<0,b>0
8.如图1,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P沿折线BE﹣ED﹣DC运动到点C时停止,点Q沿BC运动到点C停止,它们运动的速度都是1cm/s.设P、Q出发ts时,△BPQ的面积为ycm2,已知y与t的函数关系如图2所示(其中曲线OM为抛物线的一部分,其余各部分均为线段),当点P在ED上运动时,连接QD,若QD平分∠PQC,则t的值为( )
A.14﹣2
B.13﹣2
C.12﹣2
D.11﹣2
9.如图,已知OA=2,OB=4,∠AOB的平分线交AB于点C,点C坐标为(,),一动点P从O点出发,以每秒2个单位长度的速度沿y轴向点B做匀速运动,一动点Q同时从O点出发,以每秒1个单位长度的速度沿x轴向点A做匀速运动,作点P,Q关于直线OC的对称点M、N,设点P运动时间为t(0<t<2),△MNC与△OAB重叠部分的面积为S,则S关于t的函数关系图象是( )
A.
B.
C.
D.
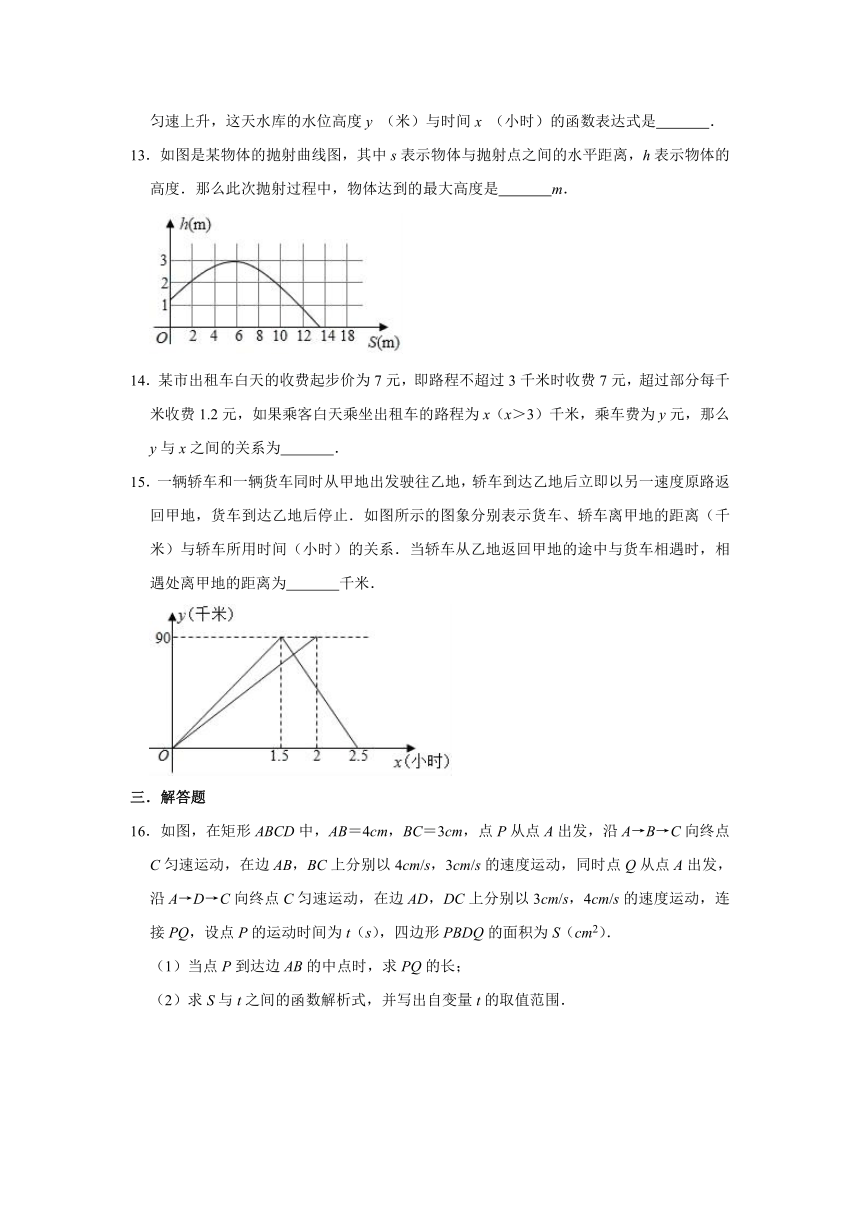
10.如图,在边长为2的正方形ABCD中,对角线AC与BD相交于点O,点P是BD上的一个动点,过点P作EF∥AC,分别交正方形的两条边于点E,F,连接OE,OF,设BP=x,△OEF的面积为y,则能大致反映y与x之间的函数关系的图象为( )
A.
B.
C.
D.
二.填空题
11.若正方形的边长为x,面积为y,则y与x之间的关系式为
(x>0).
12.某水库的水位在一天内持续上涨,初始的水位高度为8米,水位以每小时0.2米的速度匀速上升,这天水库的水位高度y
(米)与时间x
(小时)的函数表达式是
.
13.如图是某物体的抛射曲线图,其中s表示物体与抛射点之间的水平距离,h表示物体的高度.那么此次抛射过程中,物体达到的最大高度是
m.
14.某市出租车白天的收费起步价为7元,即路程不超过3千米时收费7元,超过部分每千米收费1.2元,如果乘客白天乘坐出租车的路程为x(x>3)千米,乘车费为y元,那么y与x之间的关系为
.
15.一辆轿车和一辆货车同时从甲地出发驶往乙地,轿车到达乙地后立即以另一速度原路返回甲地,货车到达乙地后停止.如图所示的图象分别表示货车、轿车离甲地的距离(千米)与轿车所用时间(小时)的关系.当轿车从乙地返回甲地的途中与货车相遇时,相遇处离甲地的距离为
千米.
三.解答题
16.如图,在矩形ABCD中,AB=4cm,BC=3cm,点P从点A出发,沿A→B→C向终点C匀速运动,在边AB,BC上分别以4cm/s,3cm/s的速度运动,同时点Q从点A出发,沿A→D→C向终点C匀速运动,在边AD,DC上分别以3cm/s,4cm/s的速度运动,连接PQ,设点P的运动时间为t(s),四边形PBDQ的面积为S(cm2).
(1)当点P到达边AB的中点时,求PQ的长;
(2)求S与t之间的函数解析式,并写出自变量t的取值范围.
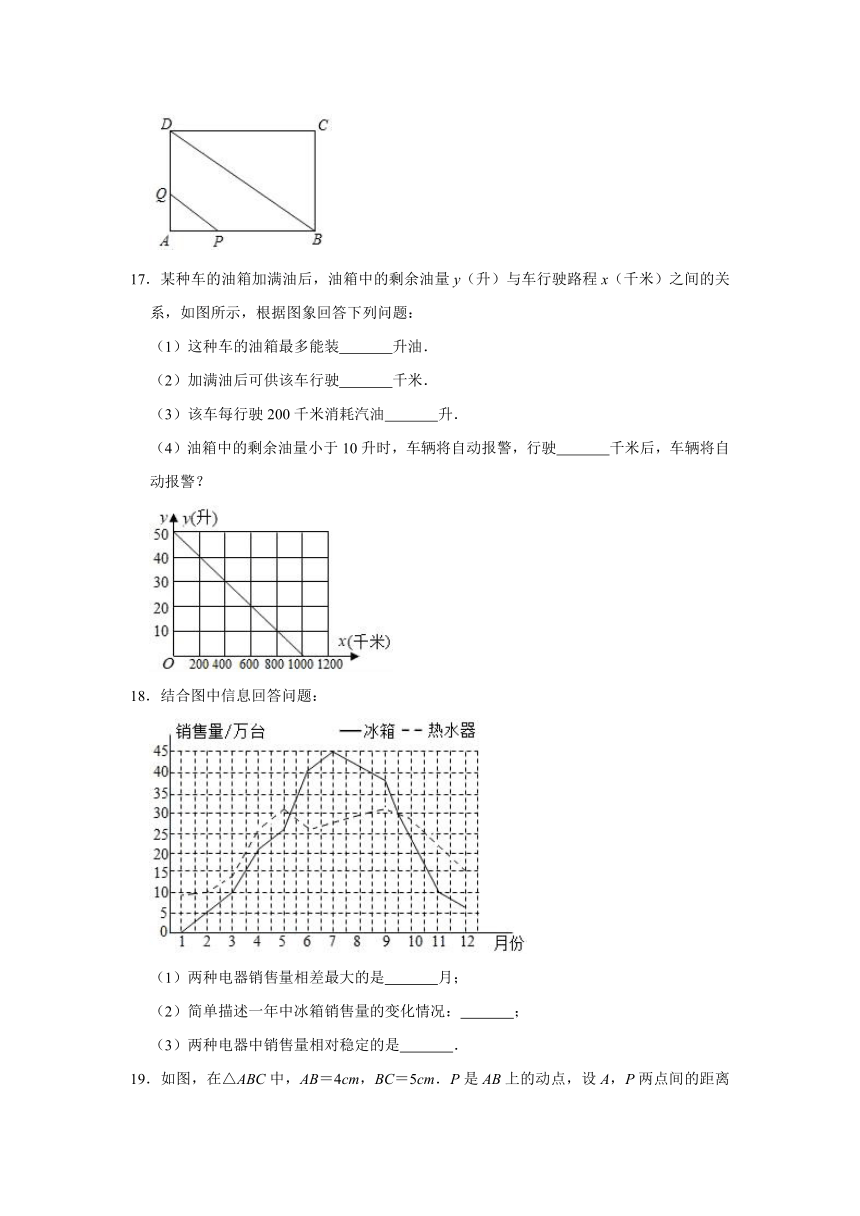
17.某种车的油箱加满油后,油箱中的剩余油量y(升)与车行驶路程x(千米)之间的关系,如图所示,根据图象回答下列问题:
(1)这种车的油箱最多能装
升油.
(2)加满油后可供该车行驶
千米.
(3)该车每行驶200千米消耗汽油
升.
(4)油箱中的剩余油量小于10升时,车辆将自动报警,行驶
千米后,车辆将自动报警?
18.结合图中信息回答问题:
(1)两种电器销售量相差最大的是
月;
(2)简单描述一年中冰箱销售量的变化情况:
;
(3)两种电器中销售量相对稳定的是
.
19.如图,在△ABC中,AB=4cm,BC=5cm.P是AB上的动点,设A,P两点间的距离为xcm,B,P两点间的距离为y1cm,C,P两点间的距离为y2cm.
小腾根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.下面是小腾的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y1,y2与x的几组对应值:
x/cm
0
1
2
3
4
y1/cm
4.00
3.69
2.13
0
y2/cm
3.00
3.91
4.71
5.23
5
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),点(x,y2),并画出函数y1,y2的图象;
(3)结合函数图象,
①当△PBC为等腰三角形时,AP的长度约为
cm;
②记AB所在圆的圆心为点O,当直线PC恰好经过点O时,PC的长度约为
cm.
参考答案与试题解析
一.选择题
1.【解答】解:由题意得,y=x=x,
故选:C.
2.【解答】解:x=﹣2时,y=2x2﹣1=7,
故选:D.
3.【解答】解:由题意得,5﹣x≥0,x﹣3≠0,
解得,x≤5且x≠3,
故选:C.
4.【解答】解:要使有意义,必须2021﹣x≠0,
解得,x≠2021,
故选:C.
5.【解答】解:A、满足对于x的每一个取值,y都有唯一确定的值与之对应关系,故此选项不符合题意;
B、满足对于x的每一个取值,y都有唯一确定的值与之对应关系,故此选项不符合题意;
C、不满足对于x的每一个取值,y都有唯一确定的值与之对应关系,故此选项符合题意;
D、满足对于x的每一个取值,y都有唯一确定的值与之对应关系,故此选项不符合题意;
故选:C.
6.【解答】解:由题意得,x﹣2≥0,x+1≠0,
解得,x≥2,
故选:A.
7.【解答】解:由图象可知,当x>0时,y<0,
∴a<0;
x=﹣b时,函数值不存在,
∴﹣b<0,
∴b>0;
故选:D.
8.【解答】解:由题意可得,
BE=5,BC=12,
∵当t=5时,S=10,
∴10=,得AB=4,
作EH⊥BC于点H,作EF∥PQ,P1Q2∥EF,作DG⊥P1Q2于点G,
则EH=AB=4,BE=BF=5,
∵∠EHB=90°,
∴BH==3,
∴HF=2,
∴EF==2,
∴P1Q2=2,
设当点P运动到P1时,Q2D平分∠P1Q2C,
则DG=DC=4,P1D=17﹣AE﹣EP1=12﹣3﹣(t﹣5)=14﹣t,
∴=,
解得:t=14﹣2,
故选:A.
9.【解答】解:如图1,过点C作CF⊥x轴于点F,CE⊥y轴于点E,
由题意P(0,2t)、Q(t,0).
∵对称轴OC为第一象限的角平分线,
∴对称点坐标为:M(2t,0),N(0,t).
当0<t≤1时,如图1所示,点M在线段OA上,重叠部分面积为S△CMN.
S△CMN=S四边形CMON﹣S△OMN=(S△COM+S△CON)﹣S△OMN=(2t×+t×)﹣2tt=﹣t2+2t;
当1<t<2时,如图2所示,点M在OA的延长线上,设MN与AB交于点D,则重叠部分面积为S△CDN.
设直线MN的解析式为y=kx+b,将M(2t,0)、N(0,t)代入得,解得,
∴y=﹣x+t;
同理求得直线AB的解析式为:y=﹣2x+4.
联立y=﹣x+t与y=﹣2x+4,求得点D的横坐标为.
S△CDN=S△BDN﹣S△BCN=(4﹣t)﹣(4﹣t)×=t2﹣2t+.
综上所述,S=.
观察图象,可知当t=1时,S有最大值,最大值为1,
故选:C.
10.【解答】解:当点P在OB上时,
∵四边形ABCD是正方形,边长为2,
∴AB=BC=2,AC⊥BD,∠ACB=∠CAB=45°,
∴AC=2,BO=DO=AO=CO=,
∵EF∥AC,
∴∠BAC=∠BEF=45°,∠BFE=∠BCA=45°,∠AOB=∠EPB=90°,
∴∠BEF=∠BFE,
∴BE=BF,
∵∠BPE=90°,
∴BP=EP=FP=x,
∴OP=﹣x,
∴y=×EF×OP=×2x×(﹣x)=﹣x2+x,(0≤x≤)
当点P在DO上时,同理可得:y=﹣x2+3x﹣4,(<x≤2),
故选:C.
二.填空题(共5小题)
11.【解答】解:∵正方形的面积等于边长乘以边长,
∴y=xx=x2,
故答案为:y=x2;
12.【解答】解:由题意得,
y=8+0.2x
(x>0),
故答案为:y=8+0.2x(x>0).
13.【解答】解:由函数图象可得,当S=6时,h有最大值3,
∴此次抛射过程中,物体达到的最大高度是3m,
故答案为:3.
14.【解答】解:依据题意得:y=7+1.2(x﹣3)=1.2x+3.4,
故答案为:y=1.2x+3.4,
15.【解答】解:由图象可得,货车的速度为:90÷2=45(千米/小时),
轿车返回时的速度为:90÷(2.5﹣1.5)=90(千米/小时),
设当轿车从乙地返回甲地的途中与货车相遇时,货车行驶的时间为a小时,
45a+90(a﹣1.5)=90,
解得,a=,
45×=75(千米),
即相遇处到甲地的距离是75千米.
故答案为:75.
三.解答题(共4小题)
16.【解答】解:(1)由题意得,当点P在线段AB上时,AP=4t,AQ=3t,
当点P到达边AB的中点时,AP=2,即4t=2,
解得,t=,
∴AQ=,
∴PQ===(cm);
(2)当点P在边AB上时,
S=×AB×AD﹣×AP×AQ
=×4×3﹣×4t×3t
=6﹣6t2(0<t<1);
当点P在边BC上时,CP=3﹣3(t﹣1)=6﹣3t,CQ=4﹣4(t﹣1)=8﹣4t,
S=×BC×CD﹣×CP×CQ
=×3×4﹣(6﹣3t)(8﹣4t)
=﹣6t2+24t﹣18(1<t<2);
17.【解答】解:(1)这种车的油箱最多能装50升油.
(2)加满油后可供该车行驶1000千米.
(3)该车每行驶200千米消耗汽油10升.
(4)油箱中的剩余油量小于10升时,车辆将自动报警,行驶800千米后,车辆将自动报警.
故答案为:(1)50;(2)1000;(3)10;(4)800.
18.【解答】解:(1)由图象可知,两种电器销售量相差最大的是7月;
(2)一年中冰箱销售量的变化情况大致为:先上升后下降,在夏季时销售量最大;
(3)两种电器中销售量相对稳定的是热水器.
故答案为:(1)7;(2)先上升后下降,在夏季时销售量最大;(3)热水器.
19.【解答】解:(1)由画图可得,x=4时,y1≈3.09cm(答案不唯一).
故答案为:3.09(答案不唯一).
(2)描点绘图如下:
(3)①由y1与y2的交点的横坐标可知,x≈0.83cm时,PC=PB,
当x≈2.49cm时,y2=5cm,即PC=BC,
观察图象可知,PB不可能等于BC,
故答案为:0.83或2.49(答案不唯一).
②当直线PC恰好经过点O时,PC的长度取得最大值,从图象看,PC=y2≈5.32cm,
故答案为5.32(答案不唯一).
一.选择题
1.如果每盒笔售价16元,共有10支,用y(元)表示笔的售价,x表示笔的支数,那么y与x的关系式为( )
A.y=10x
B.y=16x
C.y=x
D.y=x
2.根据如图所示的计算程序,若输入x=﹣2,则输出结果y的值为( )
A.﹣3
B.3
C.﹣7
D.7
3.函数y=自变量x的取值范围是( )
A.x≠3
B.x≤5
C.x≤5且x≠3
D.x<5且x≠3
4.函数y=自变量的取值范围是( )
A.x≠2020
B.x≠﹣2020
C.x≠2021
D.x≠﹣2021
5.下列图形中,不能代表y是x函数的是( )
A.
B.
C.
D.
6.函数y=中自变量x的取值范围是( )
A.x≥2
B.x≥2且x≠﹣1
C.x>2且x≠﹣1
D.x≠﹣1
7.已知关于x的函数的图象如图所示,根据探究函数图象的经验,可以推断常数a,b的值满足( )
A.a>0,b>0
B.a<0,b<0
C.a>0,b<0
D.a<0,b>0
8.如图1,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P沿折线BE﹣ED﹣DC运动到点C时停止,点Q沿BC运动到点C停止,它们运动的速度都是1cm/s.设P、Q出发ts时,△BPQ的面积为ycm2,已知y与t的函数关系如图2所示(其中曲线OM为抛物线的一部分,其余各部分均为线段),当点P在ED上运动时,连接QD,若QD平分∠PQC,则t的值为( )
A.14﹣2
B.13﹣2
C.12﹣2
D.11﹣2
9.如图,已知OA=2,OB=4,∠AOB的平分线交AB于点C,点C坐标为(,),一动点P从O点出发,以每秒2个单位长度的速度沿y轴向点B做匀速运动,一动点Q同时从O点出发,以每秒1个单位长度的速度沿x轴向点A做匀速运动,作点P,Q关于直线OC的对称点M、N,设点P运动时间为t(0<t<2),△MNC与△OAB重叠部分的面积为S,则S关于t的函数关系图象是( )
A.
B.
C.
D.
10.如图,在边长为2的正方形ABCD中,对角线AC与BD相交于点O,点P是BD上的一个动点,过点P作EF∥AC,分别交正方形的两条边于点E,F,连接OE,OF,设BP=x,△OEF的面积为y,则能大致反映y与x之间的函数关系的图象为( )
A.
B.
C.
D.
二.填空题
11.若正方形的边长为x,面积为y,则y与x之间的关系式为
(x>0).
12.某水库的水位在一天内持续上涨,初始的水位高度为8米,水位以每小时0.2米的速度匀速上升,这天水库的水位高度y
(米)与时间x
(小时)的函数表达式是
.
13.如图是某物体的抛射曲线图,其中s表示物体与抛射点之间的水平距离,h表示物体的高度.那么此次抛射过程中,物体达到的最大高度是
m.
14.某市出租车白天的收费起步价为7元,即路程不超过3千米时收费7元,超过部分每千米收费1.2元,如果乘客白天乘坐出租车的路程为x(x>3)千米,乘车费为y元,那么y与x之间的关系为
.
15.一辆轿车和一辆货车同时从甲地出发驶往乙地,轿车到达乙地后立即以另一速度原路返回甲地,货车到达乙地后停止.如图所示的图象分别表示货车、轿车离甲地的距离(千米)与轿车所用时间(小时)的关系.当轿车从乙地返回甲地的途中与货车相遇时,相遇处离甲地的距离为
千米.
三.解答题
16.如图,在矩形ABCD中,AB=4cm,BC=3cm,点P从点A出发,沿A→B→C向终点C匀速运动,在边AB,BC上分别以4cm/s,3cm/s的速度运动,同时点Q从点A出发,沿A→D→C向终点C匀速运动,在边AD,DC上分别以3cm/s,4cm/s的速度运动,连接PQ,设点P的运动时间为t(s),四边形PBDQ的面积为S(cm2).
(1)当点P到达边AB的中点时,求PQ的长;
(2)求S与t之间的函数解析式,并写出自变量t的取值范围.
17.某种车的油箱加满油后,油箱中的剩余油量y(升)与车行驶路程x(千米)之间的关系,如图所示,根据图象回答下列问题:
(1)这种车的油箱最多能装
升油.
(2)加满油后可供该车行驶
千米.
(3)该车每行驶200千米消耗汽油
升.
(4)油箱中的剩余油量小于10升时,车辆将自动报警,行驶
千米后,车辆将自动报警?
18.结合图中信息回答问题:
(1)两种电器销售量相差最大的是
月;
(2)简单描述一年中冰箱销售量的变化情况:
;
(3)两种电器中销售量相对稳定的是
.
19.如图,在△ABC中,AB=4cm,BC=5cm.P是AB上的动点,设A,P两点间的距离为xcm,B,P两点间的距离为y1cm,C,P两点间的距离为y2cm.
小腾根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.下面是小腾的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y1,y2与x的几组对应值:
x/cm
0
1
2
3
4
y1/cm
4.00
3.69
2.13
0
y2/cm
3.00
3.91
4.71
5.23
5
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),点(x,y2),并画出函数y1,y2的图象;
(3)结合函数图象,
①当△PBC为等腰三角形时,AP的长度约为
cm;
②记AB所在圆的圆心为点O,当直线PC恰好经过点O时,PC的长度约为
cm.
参考答案与试题解析
一.选择题
1.【解答】解:由题意得,y=x=x,
故选:C.
2.【解答】解:x=﹣2时,y=2x2﹣1=7,
故选:D.
3.【解答】解:由题意得,5﹣x≥0,x﹣3≠0,
解得,x≤5且x≠3,
故选:C.
4.【解答】解:要使有意义,必须2021﹣x≠0,
解得,x≠2021,
故选:C.
5.【解答】解:A、满足对于x的每一个取值,y都有唯一确定的值与之对应关系,故此选项不符合题意;
B、满足对于x的每一个取值,y都有唯一确定的值与之对应关系,故此选项不符合题意;
C、不满足对于x的每一个取值,y都有唯一确定的值与之对应关系,故此选项符合题意;
D、满足对于x的每一个取值,y都有唯一确定的值与之对应关系,故此选项不符合题意;
故选:C.
6.【解答】解:由题意得,x﹣2≥0,x+1≠0,
解得,x≥2,
故选:A.
7.【解答】解:由图象可知,当x>0时,y<0,
∴a<0;
x=﹣b时,函数值不存在,
∴﹣b<0,
∴b>0;
故选:D.
8.【解答】解:由题意可得,
BE=5,BC=12,
∵当t=5时,S=10,
∴10=,得AB=4,
作EH⊥BC于点H,作EF∥PQ,P1Q2∥EF,作DG⊥P1Q2于点G,
则EH=AB=4,BE=BF=5,
∵∠EHB=90°,
∴BH==3,
∴HF=2,
∴EF==2,
∴P1Q2=2,
设当点P运动到P1时,Q2D平分∠P1Q2C,
则DG=DC=4,P1D=17﹣AE﹣EP1=12﹣3﹣(t﹣5)=14﹣t,
∴=,
解得:t=14﹣2,
故选:A.
9.【解答】解:如图1,过点C作CF⊥x轴于点F,CE⊥y轴于点E,
由题意P(0,2t)、Q(t,0).
∵对称轴OC为第一象限的角平分线,
∴对称点坐标为:M(2t,0),N(0,t).
当0<t≤1时,如图1所示,点M在线段OA上,重叠部分面积为S△CMN.
S△CMN=S四边形CMON﹣S△OMN=(S△COM+S△CON)﹣S△OMN=(2t×+t×)﹣2tt=﹣t2+2t;
当1<t<2时,如图2所示,点M在OA的延长线上,设MN与AB交于点D,则重叠部分面积为S△CDN.
设直线MN的解析式为y=kx+b,将M(2t,0)、N(0,t)代入得,解得,
∴y=﹣x+t;
同理求得直线AB的解析式为:y=﹣2x+4.
联立y=﹣x+t与y=﹣2x+4,求得点D的横坐标为.
S△CDN=S△BDN﹣S△BCN=(4﹣t)﹣(4﹣t)×=t2﹣2t+.
综上所述,S=.
观察图象,可知当t=1时,S有最大值,最大值为1,
故选:C.
10.【解答】解:当点P在OB上时,
∵四边形ABCD是正方形,边长为2,
∴AB=BC=2,AC⊥BD,∠ACB=∠CAB=45°,
∴AC=2,BO=DO=AO=CO=,
∵EF∥AC,
∴∠BAC=∠BEF=45°,∠BFE=∠BCA=45°,∠AOB=∠EPB=90°,
∴∠BEF=∠BFE,
∴BE=BF,
∵∠BPE=90°,
∴BP=EP=FP=x,
∴OP=﹣x,
∴y=×EF×OP=×2x×(﹣x)=﹣x2+x,(0≤x≤)
当点P在DO上时,同理可得:y=﹣x2+3x﹣4,(<x≤2),
故选:C.
二.填空题(共5小题)
11.【解答】解:∵正方形的面积等于边长乘以边长,
∴y=xx=x2,
故答案为:y=x2;
12.【解答】解:由题意得,
y=8+0.2x
(x>0),
故答案为:y=8+0.2x(x>0).
13.【解答】解:由函数图象可得,当S=6时,h有最大值3,
∴此次抛射过程中,物体达到的最大高度是3m,
故答案为:3.
14.【解答】解:依据题意得:y=7+1.2(x﹣3)=1.2x+3.4,
故答案为:y=1.2x+3.4,
15.【解答】解:由图象可得,货车的速度为:90÷2=45(千米/小时),
轿车返回时的速度为:90÷(2.5﹣1.5)=90(千米/小时),
设当轿车从乙地返回甲地的途中与货车相遇时,货车行驶的时间为a小时,
45a+90(a﹣1.5)=90,
解得,a=,
45×=75(千米),
即相遇处到甲地的距离是75千米.
故答案为:75.
三.解答题(共4小题)
16.【解答】解:(1)由题意得,当点P在线段AB上时,AP=4t,AQ=3t,
当点P到达边AB的中点时,AP=2,即4t=2,
解得,t=,
∴AQ=,
∴PQ===(cm);
(2)当点P在边AB上时,
S=×AB×AD﹣×AP×AQ
=×4×3﹣×4t×3t
=6﹣6t2(0<t<1);
当点P在边BC上时,CP=3﹣3(t﹣1)=6﹣3t,CQ=4﹣4(t﹣1)=8﹣4t,
S=×BC×CD﹣×CP×CQ
=×3×4﹣(6﹣3t)(8﹣4t)
=﹣6t2+24t﹣18(1<t<2);
17.【解答】解:(1)这种车的油箱最多能装50升油.
(2)加满油后可供该车行驶1000千米.
(3)该车每行驶200千米消耗汽油10升.
(4)油箱中的剩余油量小于10升时,车辆将自动报警,行驶800千米后,车辆将自动报警.
故答案为:(1)50;(2)1000;(3)10;(4)800.
18.【解答】解:(1)由图象可知,两种电器销售量相差最大的是7月;
(2)一年中冰箱销售量的变化情况大致为:先上升后下降,在夏季时销售量最大;
(3)两种电器中销售量相对稳定的是热水器.
故答案为:(1)7;(2)先上升后下降,在夏季时销售量最大;(3)热水器.
19.【解答】解:(1)由画图可得,x=4时,y1≈3.09cm(答案不唯一).
故答案为:3.09(答案不唯一).
(2)描点绘图如下:
(3)①由y1与y2的交点的横坐标可知,x≈0.83cm时,PC=PB,
当x≈2.49cm时,y2=5cm,即PC=BC,
观察图象可知,PB不可能等于BC,
故答案为:0.83或2.49(答案不唯一).
②当直线PC恰好经过点O时,PC的长度取得最大值,从图象看,PC=y2≈5.32cm,
故答案为5.32(答案不唯一).
