人教版数学八年级下册 19.2一次函数同步测试试题(一)(word解析版)
文档属性
| 名称 | 人教版数学八年级下册 19.2一次函数同步测试试题(一)(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 156.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-15 07:44:46 | ||
图片预览

文档简介
一次函数同步测试试题(一)
一.选择题
1.下面各点中,在函数y=﹣x+3图象上的点是( )
A.(3,0)
B.(﹣2,2)
C.(2,﹣2)
D.(4,1)
2.若直线y=2x﹣1经过点A(﹣2,m),B(1,n),则m,n的大小关系正确的是( )
A.m<n
B.m>n
C.m=n
D.无法确定
3.下列说法,错误的是( )
A.平面内的点与有序实数对一一对应
B.正比例函数的图象是一条经过原点的直线
C.直线y=﹣x+2经过二、三、四象限
D.直线y=2x﹣2在y轴上的截距为﹣2
4.同一坐标系中有四条直线:l1:y=2x+3,l2:y=2x﹣3,l3:y=﹣2x+,l4:y=﹣2x﹣,其中与y轴交于点(0,﹣)的直线是( )
A.直线l1
B.直线l2
C.直线l3
D.直线l4
5.在平面直角坐标系中,一次函数y=﹣2x+6与坐标轴围成的三角形面积是( )
A.6
B.18
C.15
D.9
6.已知点(﹣4,y1),(2,y2)都在直线y=﹣12x+2上,则y1与y2的大小关系是( )
A.y1>y2
B.y1=y2
C.y1<y2
D.不能比较
7.一次函数y=x﹣2与x轴的交点坐标为( )
A.(0,2)
B.(0,﹣2)
C.(2,0)
D.(﹣2,0)
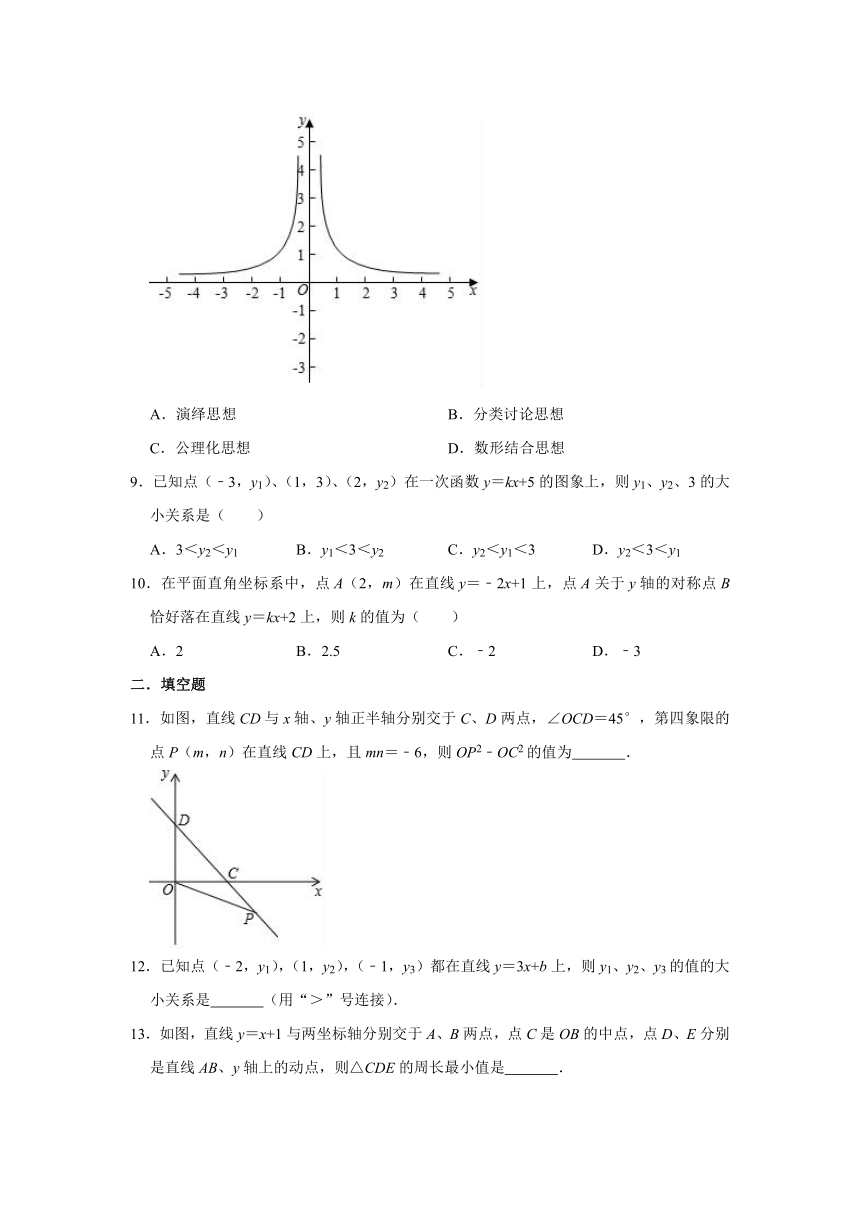
8.在经历了一次函数的学习后,同学们掌握了利用图象来分析函数性质的方法.某位同学打算探究函数y=x﹣2的性质,他先通过列表、描点、连线得到该函数的图象(如图),然后通过观察图象得到“在x的取值范围内,无论x取何值,函数值恒大于0,”的结论.其中所蕴含的数学思想是( )
A.演绎思想
B.分类讨论思想
C.公理化思想
D.数形结合思想
9.已知点(﹣3,y1)、(1,3)、(2,y2)在一次函数y=kx+5的图象上,则y1、y2、3的大小关系是( )
A.3<y2<y1
B.y1<3<y2
C.y2<y1<3
D.y2<3<y1
10.在平面直角坐标系中,点A(2,m)在直线y=﹣2x+1上,点A关于y轴的对称点B恰好落在直线y=kx+2上,则k的值为( )
A.2
B.2.5
C.﹣2
D.﹣3
二.填空题
11.如图,直线CD与x轴、y轴正半轴分别交于C、D两点,∠OCD=45°,第四象限的点P(m,n)在直线CD上,且mn=﹣6,则OP2﹣OC2的值为
.
12.已知点(﹣2,y1),(1,y2),(﹣1,y3)都在直线y=3x+b上,则y1、y2、y3的值的大小关系是
(用“>”号连接).
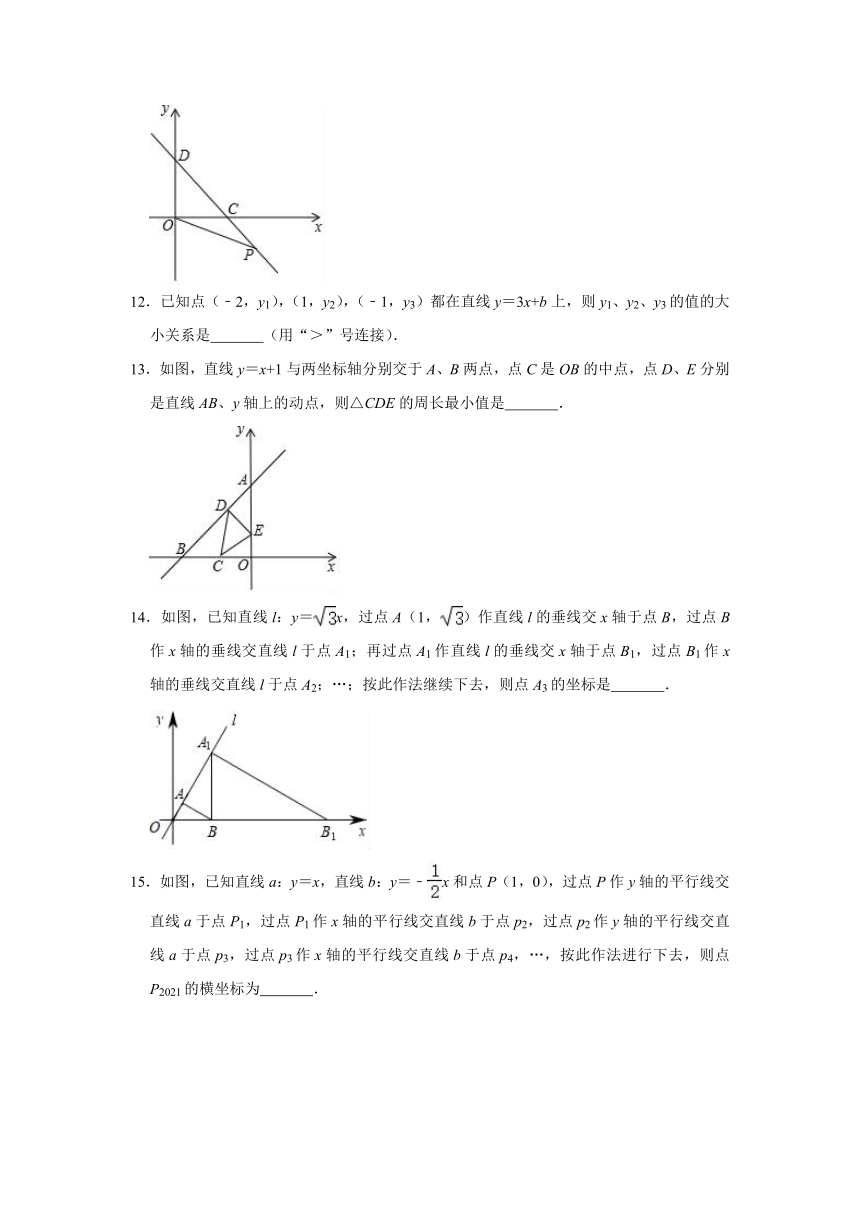
13.如图,直线y=x+1与两坐标轴分别交于A、B两点,点C是OB的中点,点D、E分别是直线AB、y轴上的动点,则△CDE的周长最小值是
.
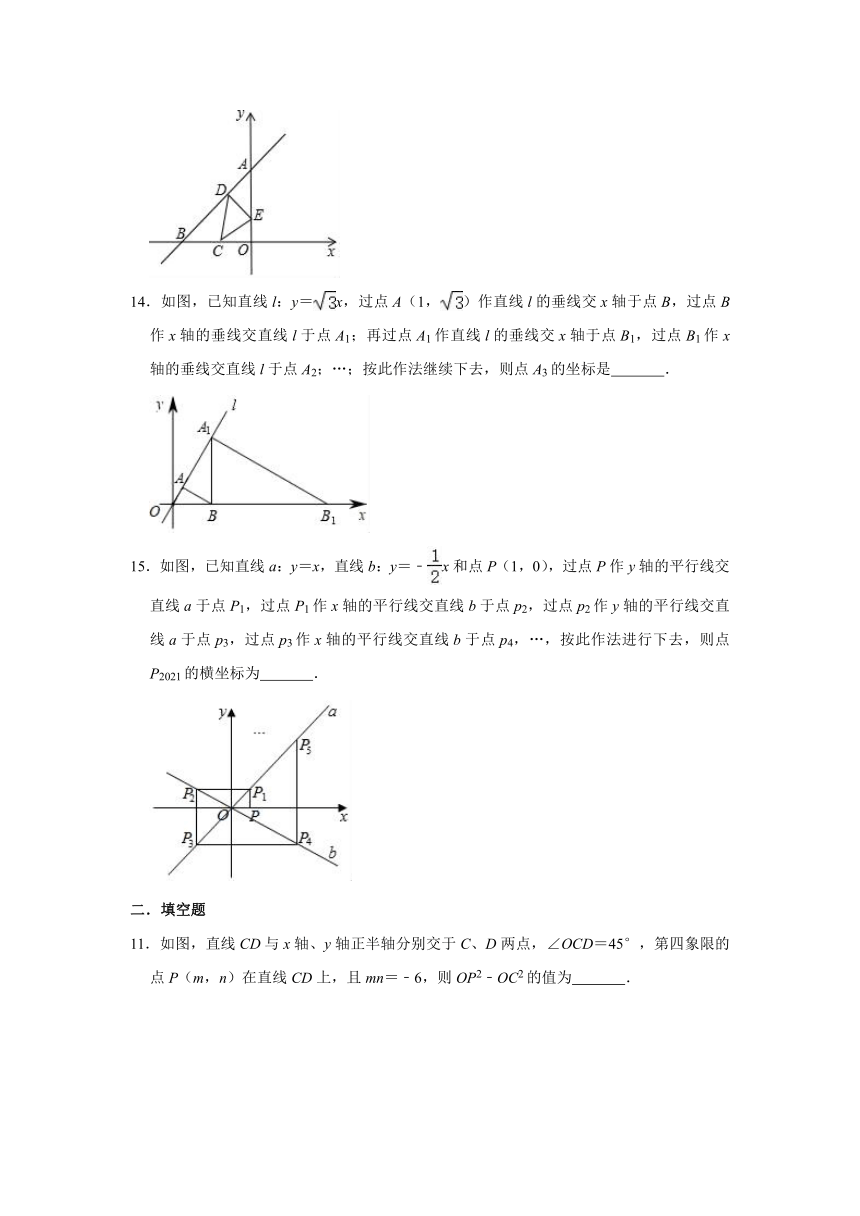
14.如图,已知直线l:y=x,过点A(1,)作直线l的垂线交x轴于点B,过点B作x轴的垂线交直线l于点A1;再过点A1作直线l的垂线交x轴于点B1,过点B1作x轴的垂线交直线l于点A2;…;按此作法继续下去,则点A3的坐标是
.
15.如图,已知直线a:y=x,直线b:y=﹣x和点P(1,0),过点P作y轴的平行线交直线a于点P1,过点P1作x轴的平行线交直线b于点p2,过点p2作y轴的平行线交直线a于点p3,过点p3作x轴的平行线交直线b于点p4,…,按此作法进行下去,则点P2021的横坐标为
.
二.填空题
11.如图,直线CD与x轴、y轴正半轴分别交于C、D两点,∠OCD=45°,第四象限的点P(m,n)在直线CD上,且mn=﹣6,则OP2﹣OC2的值为
.
12.已知点(﹣2,y1),(1,y2),(﹣1,y3)都在直线y=3x+b上,则y1、y2、y3的值的大小关系是
(用“>”号连接).
13.如图,直线y=x+1与两坐标轴分别交于A、B两点,点C是OB的中点,点D、E分别是直线AB、y轴上的动点,则△CDE的周长最小值是
.
14.如图,已知直线l:y=x,过点A(1,)作直线l的垂线交x轴于点B,过点B作x轴的垂线交直线l于点A1;再过点A1作直线l的垂线交x轴于点B1,过点B1作x轴的垂线交直线l于点A2;…;按此作法继续下去,则点A3的坐标是
.
15.如图,已知直线a:y=x,直线b:y=﹣x和点P(1,0),过点P作y轴的平行线交直线a于点P1,过点P1作x轴的平行线交直线b于点p2,过点p2作y轴的平行线交直线a于点p3,过点p3作x轴的平行线交直线b于点p4,…,按此作法进行下去,则点P2021的横坐标为
.
三.解答题
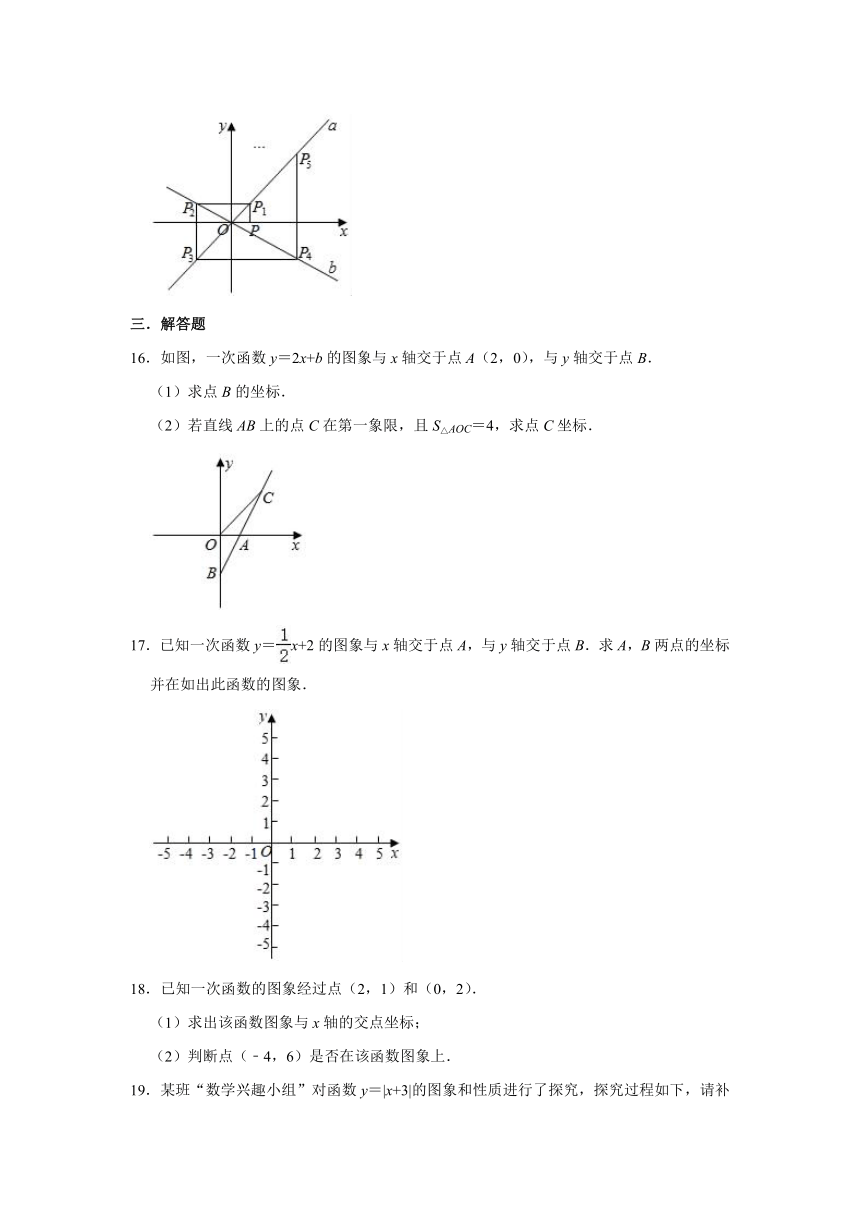
16.如图,一次函数y=2x+b的图象与x轴交于点A(2,0),与y轴交于点B.
(1)求点B的坐标.
(2)若直线AB上的点C在第一象限,且S△AOC=4,求点C坐标.
17.已知一次函数y=x+2的图象与x轴交于点A,与y轴交于点B.求A,B两点的坐标并在如出此函数的图象.
18.已知一次函数的图象经过点(2,1)和(0,2).
(1)求出该函数图象与x轴的交点坐标;
(2)判断点(﹣4,6)是否在该函数图象上.
19.某班“数学兴趣小组”对函数y=|x+3|的图象和性质进行了探究,探究过程如下,请补充完整:
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x
…
﹣7
﹣6
﹣5
﹣4
﹣3
﹣2
﹣1
0
1
…
y
…
4
3
m
1
0
1
2
3
4
…
其中,m=
.
(2)如图,在平面直角坐标系xOy中,描出了以上表格中各对对应值为坐标的点,根据描出的点,请画出函数图象;
(3)观察函数图象,写出两条函数图象的性质
;
;
(4)进一步探究函数图象发现:
①函数图象与x轴有
交点,所以对应的方程|x+3|=0有
个实数根;
②关于x的方程|x+3|=a有两个实数根时,a的取值范围是
.
参考答案与试题解析
一.选择题
1.【解答】解:A、当x=3时,y=﹣x+3=﹣+3=≠0,则(3,0)不在函数y=﹣x+3图象上,所以A选项不符合题意;
B、当x=﹣2时,y=﹣x+3=1+3=4≠2,则(﹣2,2)不在函数y=﹣x+3图象上,所以B选项不符合题意;
C、当x=2时,y=﹣x+3=﹣1+3=2≠﹣2,则(2,﹣2)不在函数y=﹣x+3图象上,所以C选项不符合;
D、当x=4时,y=﹣x+3=﹣2+3=1,则(4,1)在函数y=﹣x+3图象上,所以D选项符合题意.
故选:D.
2.【解答】解:∵k=2>0,
∴y随x的增大而增大,
又∵﹣2<1,
∴m<n.
故选:A.
3.【解答】解:A、平面内的点与有序实数对一一对应,所以A选项的说法正确;
B、正比例函数的图象是一条经过原点的直线,所以A选项的说法正确;
C、直线y=﹣x+2经过第一、二、四象限,所以C选项的说法不正确;
D、直线y=2x﹣2在y轴上的截距为﹣2,所以D选项的说法正确.
故选:C.
4.【解答】解:把x=0代入l1:y=2x+3,得y=3,
∴直线l1:y=2x+3与y轴的交点为(0,3);
把x=0代入l2:y=2x﹣3,得y=﹣3,
∴直线l2:y=2x﹣3与y轴的交点为(0,﹣3);
把x=0代入l3:y=﹣2x+,得y=,
∴直线l3:y=﹣2x+与y轴的交点为(0,);
把x=0代入l4:y=﹣2x﹣,得y=﹣,
∴直线l4:y=﹣2x﹣与y轴的交点为(0,﹣);
故选:D.
5.【解答】解:当x=0时,y=﹣2×0+6=6,
∴一次函数y=﹣2x+6的图象与y轴交于点(0,6);
当y=0时,﹣2x+6=0,解得:x=3,
∴一次函数y=﹣2x+6的图象与x轴交于点(3,0),
∴一次函数y=﹣2x+6的图象与坐标轴围成的三角形面积=×6×3=9.
故选:D.
6.【解答】解:∵k=﹣12<0,
∴y随x的增大而减小,
又∵﹣4<2,
∴y1>y2.
故选:A.
7.【解答】解:当y=0时,x﹣2=0,
解得:x=2,
∴一次函数y=x﹣2的图象与x轴的交点坐标为(2,0).
故选:C.
8.【解答】解:探究函数y=x﹣2的性质,他先通过列表、描点、连线得到该函数的图象(如图),然后通过观察图象得到“在x的取值范围内,无论x取何值,函数值恒大于0,”的结论,其中所蕴含的数学思想是数形结合思想.
故选:D.
9.【解答】解:∵(1,3)在一次函数y=kx+5的图象上,
∴3=k+5,
解得:k=﹣2,
∴函数解析式为y=﹣2x+5,
∵点(﹣3,y1)、(2,y2)在一次函数y=﹣2x+5的图象上,
∴y1=6+5=11,
y2=﹣4+5=1,
∵1<3<11,
∴y2<3<y1,
故选:D.
10.【解答】解:∵点A在直线y=﹣2x+1上,
∴m=﹣2×2+1=﹣3,
∴点A的坐标为(2,﹣3).
又∵点A、B关于y轴对称,
∴点B的坐标为(﹣2,﹣3),
∵点B(﹣2,﹣3)在直线y=kx+2上,
∴﹣3=﹣2k+2,解得:k=2.5.
故选:B.
二.填空题(共5小题)
11.【解答】解:如图,过P作PE⊥y轴于E,则OC∥PE,
∴∠OCD=∠DPE=45°,
∵∠DOC=∠DEP=90°,
∴OD=OC,DE=EP,
∵P(m,n),
∴m=OD﹣n,
∴OD=m+n,
两边同时平方得:OD2=m2+n2+2mn,
∵mn=﹣6,
∴m2+n2=OD2+12,
由勾股定理得:OP2﹣OC2=m2+(﹣n)2﹣OD2=OD2+12﹣OD2=12,
故答案为12.
12.【解答】解:∵k=3>0,
∴y随x的增大而增大,
又∵1>﹣1>﹣2,
∴y2>y3<y1.
故答案为:y2>y3<y1.
13.【解答】解:如图,作点C关于AB的对称点F,关于AO的对称点G,连接FG分别交AB、OA于点D、E,此时三角形CDE的周长最小,
∵直线y=x+1与两坐标轴分别交于A、B两点,
∴A(0,1),B(﹣1,0),
∴OA=OB,
∴∠ABC=45°,
∴△BCF是等腰直角三角形,
∵点C是OB的中点,
∴C(,0),
∴OG=,BG=,
∴BF=BC=,
由轴对称的性质,可得DF=DC,EC=EG,
△CDE的周长=CD+DE+CE=DF+DE+EG=FG,
此时△DEC周长最小,
∵Rt△BFG中,FG===,
∴△CDE周长的最小值是.
故答案为.
14.【解答】解:∵直线l:y=x,
∴∠AOB=60°,
∵A(1,),
∴OA==2,
∵AB⊥直线l,
∴OB=2OA=4,
又∵A1B⊥x轴,
∴A1B=4,
∴A1(4,4),
∴OA1==8,
∴OB1=2OA1=16,
∴A2B1=16,
∴A2(16,16),
……
∴An(22n,22n),
由此可得,点A3的坐标为(26,26)即(64,64),
故答案为(64,64).
15.【解答】解:∵点P(1,0),P1在直线y=x上,
∴P1(1,1),
∵P1P2∥x轴,
∴P2的纵坐标=P1的纵坐标=1,
∵P2在直线y=﹣x上,
∴1=﹣x,
∴x=﹣2,
∴P2(﹣2,1),即P2的横坐标为﹣2=﹣21,
同理,P3的横坐标为﹣2=﹣21,P4的横坐标为4=22,P5=22,P6=﹣23,P7=﹣23,P8=24…,
∴P4n=2,
∴P2020的横坐标为2=21010,
∴P2021的横坐标为21010,
故答案为21010.
三.解答题(共4小题)
16.【解答】解:(1)将A(2,0)代入直线y=2x+b中,得2×2+b=0
解得b=﹣4,
∴y=2x﹣4,
把x=0代入y=2x﹣4得,y=﹣4,
∴B(0,﹣4);
(2)∵S△AOC=4,点A(2,0),
∴OA=2,
∴OAyC=4,解得yC=4,
把y=4代入y=2x﹣4得2x﹣4=4,
解得x=4,
∴C(4,4).
17.【解答】解:(1)令y=0,则x=﹣4;令x=0,则y=2;
∴点A坐标为(﹣4,0);
点B坐标为(0,2),
(2)函数y=x+2的图象如下:
.
18.【解答】解:(1)设该函数解析式为y=kx+b,
把点(2,1)和(0,﹣2)代入解析式得2k+b=1,b=﹣2,
解得k=,b=﹣2,
∴该函数解析式为y=x﹣2;
令y=0,则x﹣2=0,解得x=,
∴该函数图象与x轴的交点为(,0);
(2)当x=﹣4时,y=×(﹣4)﹣2=﹣8≠6,
∴点(﹣4,6)不在该函数图象上.
19.【解答】解:(1)x=﹣5时,y=|x+3|=2,故m=2,
故答案为2.
(2)函数图象如图所示:
(3)由图象可知:是轴对称图形,当x>﹣3时,y随x的增大而增大,x<﹣3时,y随x的增大而减少;
故答案为是轴对称图形,当x>﹣3时,y随x的增大而增大,x<﹣3时,y随x的增大而减少;
(4)①函数图象与x轴有1个交点,所以对应的方程|x+3|=0有1个实数根;
故答案为1个,1;
②关于x的方程|x+3|=a有两个实数根,则a的取值范围是a>0,
故答案为a>0.
一.选择题
1.下面各点中,在函数y=﹣x+3图象上的点是( )
A.(3,0)
B.(﹣2,2)
C.(2,﹣2)
D.(4,1)
2.若直线y=2x﹣1经过点A(﹣2,m),B(1,n),则m,n的大小关系正确的是( )
A.m<n
B.m>n
C.m=n
D.无法确定
3.下列说法,错误的是( )
A.平面内的点与有序实数对一一对应
B.正比例函数的图象是一条经过原点的直线
C.直线y=﹣x+2经过二、三、四象限
D.直线y=2x﹣2在y轴上的截距为﹣2
4.同一坐标系中有四条直线:l1:y=2x+3,l2:y=2x﹣3,l3:y=﹣2x+,l4:y=﹣2x﹣,其中与y轴交于点(0,﹣)的直线是( )
A.直线l1
B.直线l2
C.直线l3
D.直线l4
5.在平面直角坐标系中,一次函数y=﹣2x+6与坐标轴围成的三角形面积是( )
A.6
B.18
C.15
D.9
6.已知点(﹣4,y1),(2,y2)都在直线y=﹣12x+2上,则y1与y2的大小关系是( )
A.y1>y2
B.y1=y2
C.y1<y2
D.不能比较
7.一次函数y=x﹣2与x轴的交点坐标为( )
A.(0,2)
B.(0,﹣2)
C.(2,0)
D.(﹣2,0)
8.在经历了一次函数的学习后,同学们掌握了利用图象来分析函数性质的方法.某位同学打算探究函数y=x﹣2的性质,他先通过列表、描点、连线得到该函数的图象(如图),然后通过观察图象得到“在x的取值范围内,无论x取何值,函数值恒大于0,”的结论.其中所蕴含的数学思想是( )
A.演绎思想
B.分类讨论思想
C.公理化思想
D.数形结合思想
9.已知点(﹣3,y1)、(1,3)、(2,y2)在一次函数y=kx+5的图象上,则y1、y2、3的大小关系是( )
A.3<y2<y1
B.y1<3<y2
C.y2<y1<3
D.y2<3<y1
10.在平面直角坐标系中,点A(2,m)在直线y=﹣2x+1上,点A关于y轴的对称点B恰好落在直线y=kx+2上,则k的值为( )
A.2
B.2.5
C.﹣2
D.﹣3
二.填空题
11.如图,直线CD与x轴、y轴正半轴分别交于C、D两点,∠OCD=45°,第四象限的点P(m,n)在直线CD上,且mn=﹣6,则OP2﹣OC2的值为
.
12.已知点(﹣2,y1),(1,y2),(﹣1,y3)都在直线y=3x+b上,则y1、y2、y3的值的大小关系是
(用“>”号连接).
13.如图,直线y=x+1与两坐标轴分别交于A、B两点,点C是OB的中点,点D、E分别是直线AB、y轴上的动点,则△CDE的周长最小值是
.
14.如图,已知直线l:y=x,过点A(1,)作直线l的垂线交x轴于点B,过点B作x轴的垂线交直线l于点A1;再过点A1作直线l的垂线交x轴于点B1,过点B1作x轴的垂线交直线l于点A2;…;按此作法继续下去,则点A3的坐标是
.
15.如图,已知直线a:y=x,直线b:y=﹣x和点P(1,0),过点P作y轴的平行线交直线a于点P1,过点P1作x轴的平行线交直线b于点p2,过点p2作y轴的平行线交直线a于点p3,过点p3作x轴的平行线交直线b于点p4,…,按此作法进行下去,则点P2021的横坐标为
.
二.填空题
11.如图,直线CD与x轴、y轴正半轴分别交于C、D两点,∠OCD=45°,第四象限的点P(m,n)在直线CD上,且mn=﹣6,则OP2﹣OC2的值为
.
12.已知点(﹣2,y1),(1,y2),(﹣1,y3)都在直线y=3x+b上,则y1、y2、y3的值的大小关系是
(用“>”号连接).
13.如图,直线y=x+1与两坐标轴分别交于A、B两点,点C是OB的中点,点D、E分别是直线AB、y轴上的动点,则△CDE的周长最小值是
.
14.如图,已知直线l:y=x,过点A(1,)作直线l的垂线交x轴于点B,过点B作x轴的垂线交直线l于点A1;再过点A1作直线l的垂线交x轴于点B1,过点B1作x轴的垂线交直线l于点A2;…;按此作法继续下去,则点A3的坐标是
.
15.如图,已知直线a:y=x,直线b:y=﹣x和点P(1,0),过点P作y轴的平行线交直线a于点P1,过点P1作x轴的平行线交直线b于点p2,过点p2作y轴的平行线交直线a于点p3,过点p3作x轴的平行线交直线b于点p4,…,按此作法进行下去,则点P2021的横坐标为
.
三.解答题
16.如图,一次函数y=2x+b的图象与x轴交于点A(2,0),与y轴交于点B.
(1)求点B的坐标.
(2)若直线AB上的点C在第一象限,且S△AOC=4,求点C坐标.
17.已知一次函数y=x+2的图象与x轴交于点A,与y轴交于点B.求A,B两点的坐标并在如出此函数的图象.
18.已知一次函数的图象经过点(2,1)和(0,2).
(1)求出该函数图象与x轴的交点坐标;
(2)判断点(﹣4,6)是否在该函数图象上.
19.某班“数学兴趣小组”对函数y=|x+3|的图象和性质进行了探究,探究过程如下,请补充完整:
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x
…
﹣7
﹣6
﹣5
﹣4
﹣3
﹣2
﹣1
0
1
…
y
…
4
3
m
1
0
1
2
3
4
…
其中,m=
.
(2)如图,在平面直角坐标系xOy中,描出了以上表格中各对对应值为坐标的点,根据描出的点,请画出函数图象;
(3)观察函数图象,写出两条函数图象的性质
;
;
(4)进一步探究函数图象发现:
①函数图象与x轴有
交点,所以对应的方程|x+3|=0有
个实数根;
②关于x的方程|x+3|=a有两个实数根时,a的取值范围是
.
参考答案与试题解析
一.选择题
1.【解答】解:A、当x=3时,y=﹣x+3=﹣+3=≠0,则(3,0)不在函数y=﹣x+3图象上,所以A选项不符合题意;
B、当x=﹣2时,y=﹣x+3=1+3=4≠2,则(﹣2,2)不在函数y=﹣x+3图象上,所以B选项不符合题意;
C、当x=2时,y=﹣x+3=﹣1+3=2≠﹣2,则(2,﹣2)不在函数y=﹣x+3图象上,所以C选项不符合;
D、当x=4时,y=﹣x+3=﹣2+3=1,则(4,1)在函数y=﹣x+3图象上,所以D选项符合题意.
故选:D.
2.【解答】解:∵k=2>0,
∴y随x的增大而增大,
又∵﹣2<1,
∴m<n.
故选:A.
3.【解答】解:A、平面内的点与有序实数对一一对应,所以A选项的说法正确;
B、正比例函数的图象是一条经过原点的直线,所以A选项的说法正确;
C、直线y=﹣x+2经过第一、二、四象限,所以C选项的说法不正确;
D、直线y=2x﹣2在y轴上的截距为﹣2,所以D选项的说法正确.
故选:C.
4.【解答】解:把x=0代入l1:y=2x+3,得y=3,
∴直线l1:y=2x+3与y轴的交点为(0,3);
把x=0代入l2:y=2x﹣3,得y=﹣3,
∴直线l2:y=2x﹣3与y轴的交点为(0,﹣3);
把x=0代入l3:y=﹣2x+,得y=,
∴直线l3:y=﹣2x+与y轴的交点为(0,);
把x=0代入l4:y=﹣2x﹣,得y=﹣,
∴直线l4:y=﹣2x﹣与y轴的交点为(0,﹣);
故选:D.
5.【解答】解:当x=0时,y=﹣2×0+6=6,
∴一次函数y=﹣2x+6的图象与y轴交于点(0,6);
当y=0时,﹣2x+6=0,解得:x=3,
∴一次函数y=﹣2x+6的图象与x轴交于点(3,0),
∴一次函数y=﹣2x+6的图象与坐标轴围成的三角形面积=×6×3=9.
故选:D.
6.【解答】解:∵k=﹣12<0,
∴y随x的增大而减小,
又∵﹣4<2,
∴y1>y2.
故选:A.
7.【解答】解:当y=0时,x﹣2=0,
解得:x=2,
∴一次函数y=x﹣2的图象与x轴的交点坐标为(2,0).
故选:C.
8.【解答】解:探究函数y=x﹣2的性质,他先通过列表、描点、连线得到该函数的图象(如图),然后通过观察图象得到“在x的取值范围内,无论x取何值,函数值恒大于0,”的结论,其中所蕴含的数学思想是数形结合思想.
故选:D.
9.【解答】解:∵(1,3)在一次函数y=kx+5的图象上,
∴3=k+5,
解得:k=﹣2,
∴函数解析式为y=﹣2x+5,
∵点(﹣3,y1)、(2,y2)在一次函数y=﹣2x+5的图象上,
∴y1=6+5=11,
y2=﹣4+5=1,
∵1<3<11,
∴y2<3<y1,
故选:D.
10.【解答】解:∵点A在直线y=﹣2x+1上,
∴m=﹣2×2+1=﹣3,
∴点A的坐标为(2,﹣3).
又∵点A、B关于y轴对称,
∴点B的坐标为(﹣2,﹣3),
∵点B(﹣2,﹣3)在直线y=kx+2上,
∴﹣3=﹣2k+2,解得:k=2.5.
故选:B.
二.填空题(共5小题)
11.【解答】解:如图,过P作PE⊥y轴于E,则OC∥PE,
∴∠OCD=∠DPE=45°,
∵∠DOC=∠DEP=90°,
∴OD=OC,DE=EP,
∵P(m,n),
∴m=OD﹣n,
∴OD=m+n,
两边同时平方得:OD2=m2+n2+2mn,
∵mn=﹣6,
∴m2+n2=OD2+12,
由勾股定理得:OP2﹣OC2=m2+(﹣n)2﹣OD2=OD2+12﹣OD2=12,
故答案为12.
12.【解答】解:∵k=3>0,
∴y随x的增大而增大,
又∵1>﹣1>﹣2,
∴y2>y3<y1.
故答案为:y2>y3<y1.
13.【解答】解:如图,作点C关于AB的对称点F,关于AO的对称点G,连接FG分别交AB、OA于点D、E,此时三角形CDE的周长最小,
∵直线y=x+1与两坐标轴分别交于A、B两点,
∴A(0,1),B(﹣1,0),
∴OA=OB,
∴∠ABC=45°,
∴△BCF是等腰直角三角形,
∵点C是OB的中点,
∴C(,0),
∴OG=,BG=,
∴BF=BC=,
由轴对称的性质,可得DF=DC,EC=EG,
△CDE的周长=CD+DE+CE=DF+DE+EG=FG,
此时△DEC周长最小,
∵Rt△BFG中,FG===,
∴△CDE周长的最小值是.
故答案为.
14.【解答】解:∵直线l:y=x,
∴∠AOB=60°,
∵A(1,),
∴OA==2,
∵AB⊥直线l,
∴OB=2OA=4,
又∵A1B⊥x轴,
∴A1B=4,
∴A1(4,4),
∴OA1==8,
∴OB1=2OA1=16,
∴A2B1=16,
∴A2(16,16),
……
∴An(22n,22n),
由此可得,点A3的坐标为(26,26)即(64,64),
故答案为(64,64).
15.【解答】解:∵点P(1,0),P1在直线y=x上,
∴P1(1,1),
∵P1P2∥x轴,
∴P2的纵坐标=P1的纵坐标=1,
∵P2在直线y=﹣x上,
∴1=﹣x,
∴x=﹣2,
∴P2(﹣2,1),即P2的横坐标为﹣2=﹣21,
同理,P3的横坐标为﹣2=﹣21,P4的横坐标为4=22,P5=22,P6=﹣23,P7=﹣23,P8=24…,
∴P4n=2,
∴P2020的横坐标为2=21010,
∴P2021的横坐标为21010,
故答案为21010.
三.解答题(共4小题)
16.【解答】解:(1)将A(2,0)代入直线y=2x+b中,得2×2+b=0
解得b=﹣4,
∴y=2x﹣4,
把x=0代入y=2x﹣4得,y=﹣4,
∴B(0,﹣4);
(2)∵S△AOC=4,点A(2,0),
∴OA=2,
∴OAyC=4,解得yC=4,
把y=4代入y=2x﹣4得2x﹣4=4,
解得x=4,
∴C(4,4).
17.【解答】解:(1)令y=0,则x=﹣4;令x=0,则y=2;
∴点A坐标为(﹣4,0);
点B坐标为(0,2),
(2)函数y=x+2的图象如下:
.
18.【解答】解:(1)设该函数解析式为y=kx+b,
把点(2,1)和(0,﹣2)代入解析式得2k+b=1,b=﹣2,
解得k=,b=﹣2,
∴该函数解析式为y=x﹣2;
令y=0,则x﹣2=0,解得x=,
∴该函数图象与x轴的交点为(,0);
(2)当x=﹣4时,y=×(﹣4)﹣2=﹣8≠6,
∴点(﹣4,6)不在该函数图象上.
19.【解答】解:(1)x=﹣5时,y=|x+3|=2,故m=2,
故答案为2.
(2)函数图象如图所示:
(3)由图象可知:是轴对称图形,当x>﹣3时,y随x的增大而增大,x<﹣3时,y随x的增大而减少;
故答案为是轴对称图形,当x>﹣3时,y随x的增大而增大,x<﹣3时,y随x的增大而减少;
(4)①函数图象与x轴有1个交点,所以对应的方程|x+3|=0有1个实数根;
故答案为1个,1;
②关于x的方程|x+3|=a有两个实数根,则a的取值范围是a>0,
故答案为a>0.
