2.4.1平面向量数量积的物理背景及其含义
文档属性
| 名称 | 2.4.1平面向量数量积的物理背景及其含义 |  | |
| 格式 | rar | ||
| 文件大小 | 7.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-11-29 20:13:56 | ||
图片预览











文档简介
(共37张PPT)
2.4.1平面向量数量积的物理背景及其含义
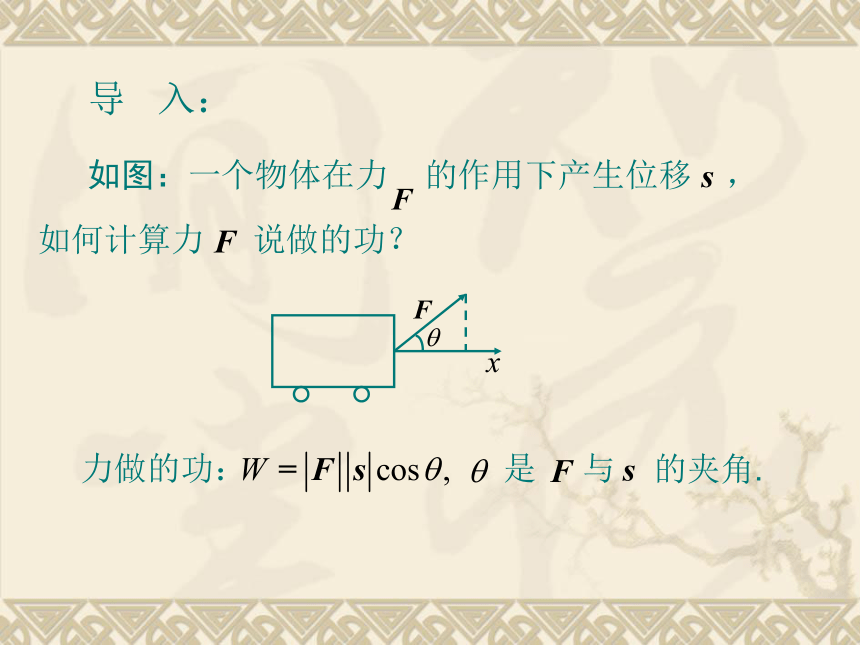
如图:一个物体在力
的作用下产生位移
,
如何计算力
说做的功?
力做的功:
是
与
的夹角.
导 入:
向量的数量积(或内积)定义
叫做向量
和
的数量积(或内积),
记作
,即
其中
是
与
的夹角.
注意:两个向量的数量积是一个实数,可以是正数,负数,零.
投影:
零向量与任一向量的数量积为0.
思考:
2.投影的正负与什么有关?
1.投影是一个数量还是一个向量?
向量的数量积的几何意义
由投影的意义,我们可以得到
的几何
意义:数量积
等于
的长度
与
在
的方向上的投影
的乘积.
两个向量数量积的性质
数量积的运算律:
例2:求证:
证明:
的夹角为
总结:
1.数量积的概念;
2.投影的概念;
3.两个向量数量积的性质;
4.数量积的几何意义.
作业:
习题2.4A组第2,4,题
习题2.4B组第1题
莓础梳理
1.向量的数量积的定义
已知两个非零向量a与b,则把数量| all b cose0叫做a与
b的数量积(或内积),记作a·b,即a·b= abl cos其中0
是a与b的夹角,acos以(bcos0)叫做向量a在b方向上(b
在a方向上)的投影
规定零向量与任一向量的数量积均为0
思考讨论y向量的数量积与数乘向量的区别是什么
提示:向量的数量积a·方是一个实数,不考虑方向
数乘向量λa是一个向量,既有大小,又有方向,这是二者的
主要区别
2.向量的数量积的几何意义
a·b的几何意义是数量积a·b等于a的长度|a|与
b在a的方向上的投影|bcos0的乘积
层考讨论为
3.向量的数量积的性质
设a与b都是非零向量,0为a与b的夹角
(1)a⊥b→a·b=0;
2)当a与b同向时,a·b=|a||b
当a与b反向时,a·b
b
(3)a·a=a2或|a|=
(4)cos0
(5)
4.向量数量积的运算律
已知向量a,b,c与实数λ,则
交换律
结合律
(λa)·b=A(a·b)=a·(入b)
分配律
a·(b+c)=a·b+a·c
思考讨论》对于向量a,b,,等式(a·b).c=a
(b·c)一定成立吗
提示:不一定成立,∵若(a·b)·c≠0,其方向与c
相同或相反,而a·(b·c)≠0时其方向与a相同或相反,而
a与c不一定方向相同,故该等式不一定成立
2.4.1平面向量数量积的物理背景及其含义
如图:一个物体在力
的作用下产生位移
,
如何计算力
说做的功?
力做的功:
是
与
的夹角.
导 入:
向量的数量积(或内积)定义
叫做向量
和
的数量积(或内积),
记作
,即
其中
是
与
的夹角.
注意:两个向量的数量积是一个实数,可以是正数,负数,零.
投影:
零向量与任一向量的数量积为0.
思考:
2.投影的正负与什么有关?
1.投影是一个数量还是一个向量?
向量的数量积的几何意义
由投影的意义,我们可以得到
的几何
意义:数量积
等于
的长度
与
在
的方向上的投影
的乘积.
两个向量数量积的性质
数量积的运算律:
例2:求证:
证明:
的夹角为
总结:
1.数量积的概念;
2.投影的概念;
3.两个向量数量积的性质;
4.数量积的几何意义.
作业:
习题2.4A组第2,4,题
习题2.4B组第1题
莓础梳理
1.向量的数量积的定义
已知两个非零向量a与b,则把数量| all b cose0叫做a与
b的数量积(或内积),记作a·b,即a·b= abl cos其中0
是a与b的夹角,acos以(bcos0)叫做向量a在b方向上(b
在a方向上)的投影
规定零向量与任一向量的数量积均为0
思考讨论y向量的数量积与数乘向量的区别是什么
提示:向量的数量积a·方是一个实数,不考虑方向
数乘向量λa是一个向量,既有大小,又有方向,这是二者的
主要区别
2.向量的数量积的几何意义
a·b的几何意义是数量积a·b等于a的长度|a|与
b在a的方向上的投影|bcos0的乘积
层考讨论为
3.向量的数量积的性质
设a与b都是非零向量,0为a与b的夹角
(1)a⊥b→a·b=0;
2)当a与b同向时,a·b=|a||b
当a与b反向时,a·b
b
(3)a·a=a2或|a|=
(4)cos0
(5)
4.向量数量积的运算律
已知向量a,b,c与实数λ,则
交换律
结合律
(λa)·b=A(a·b)=a·(入b)
分配律
a·(b+c)=a·b+a·c
思考讨论》对于向量a,b,,等式(a·b).c=a
(b·c)一定成立吗
提示:不一定成立,∵若(a·b)·c≠0,其方向与c
相同或相反,而a·(b·c)≠0时其方向与a相同或相反,而
a与c不一定方向相同,故该等式不一定成立
