2．4正态分布 精品课件

(共48张PPT)
2.4 正态分布
高二数学 选修2-3
引入
正态分布在统计学中是很重要的分布。我们知道，离散型随机变量最多取可列个不同值，它等于某一特定实数的概率可能大于0，人们感兴趣的是它取某些特定值的概率，即感兴趣的是其分布列；连续型随机变量可能取某个区间上的任何值，它等于任何一个实数的概率都为0，所以通常感兴趣的是它落在某个区间的概率。离散型随机变量的概率分布规律用分布列描述，而连续型随机变量的概率分布规律用密度函数（曲线）描述。
复习
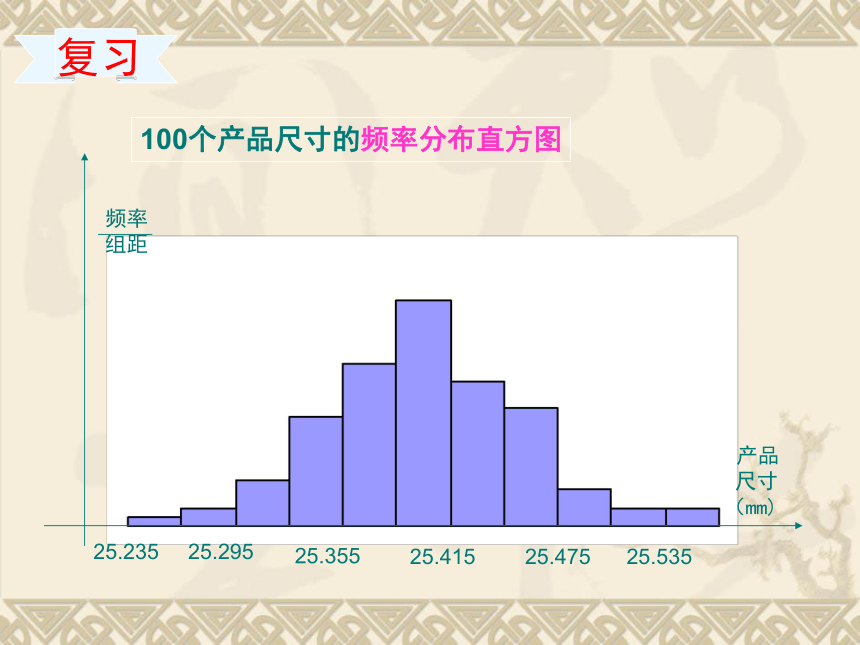
100个产品尺寸的频率分布直方图
25.235
25.295
25.355
25.415
25.475
25.535
产品
尺寸
（mm)
频率
组距
复习
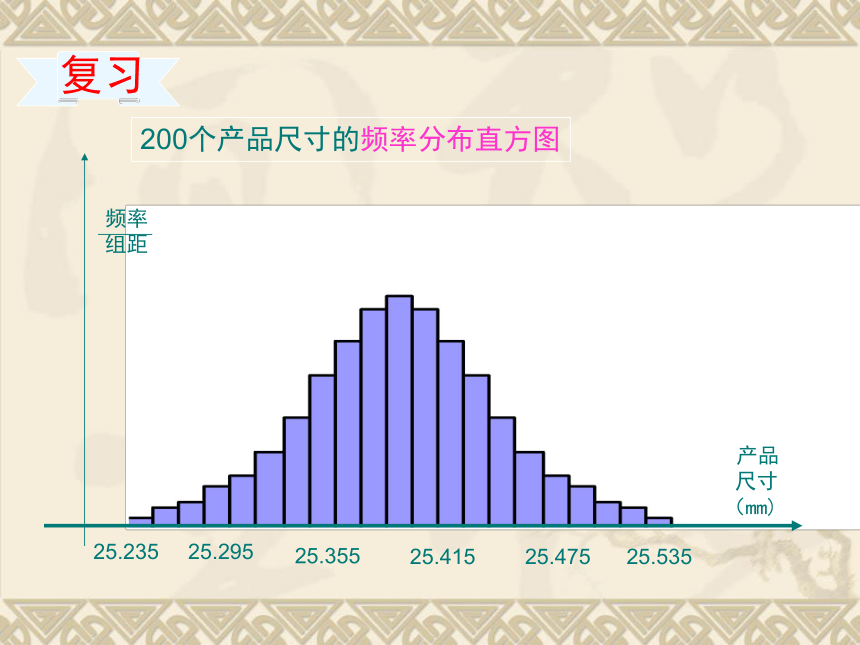
200个产品尺寸的频率分布直方图
25.235
25.295
25.355
25.415
25.475
25.535
产品
尺寸
（mm)
频率
组距
复习
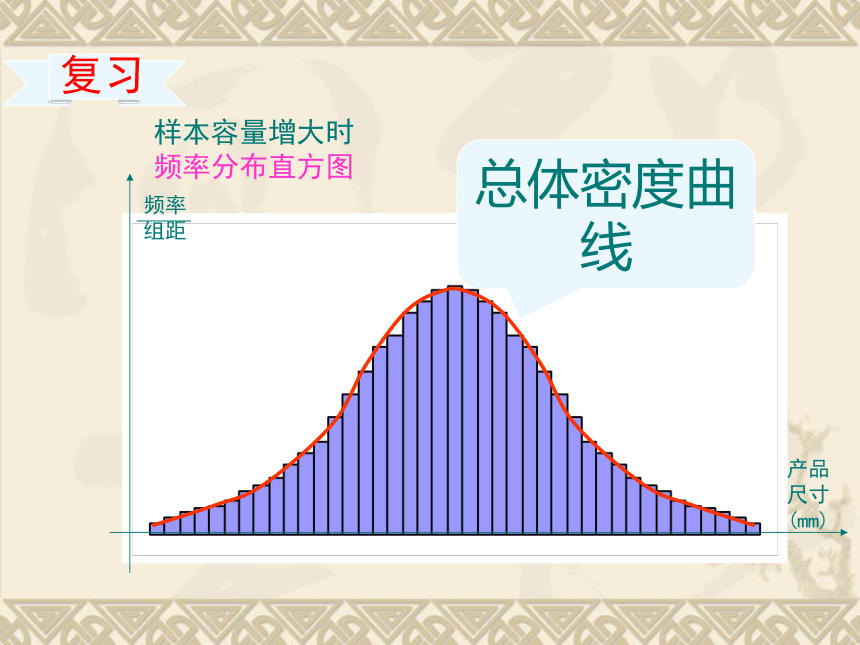
样本容量增大时
频率分布直方图
频率
组距
产品
尺寸
(mm)
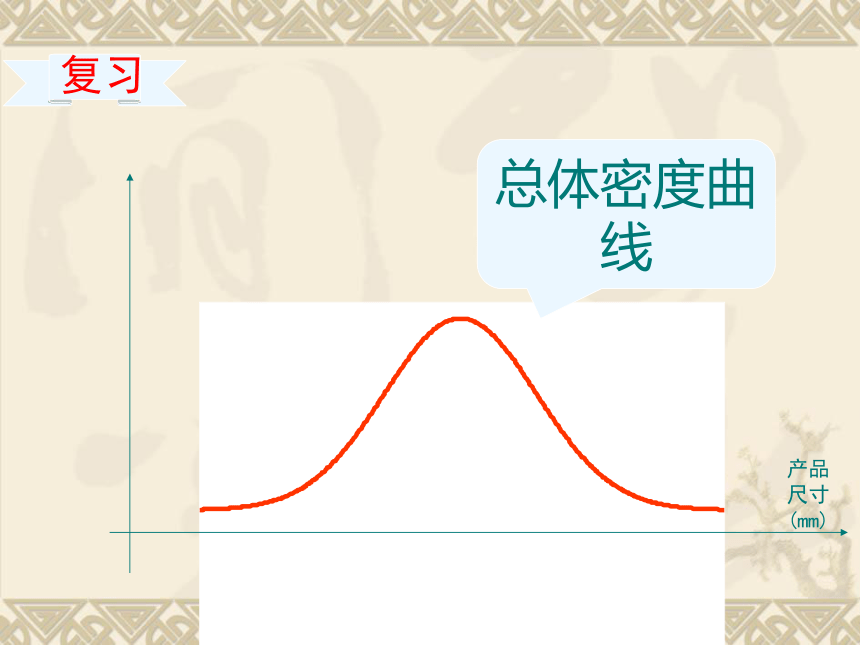
总体密度曲线
复习
产品
尺寸
(mm)
总体密度曲线
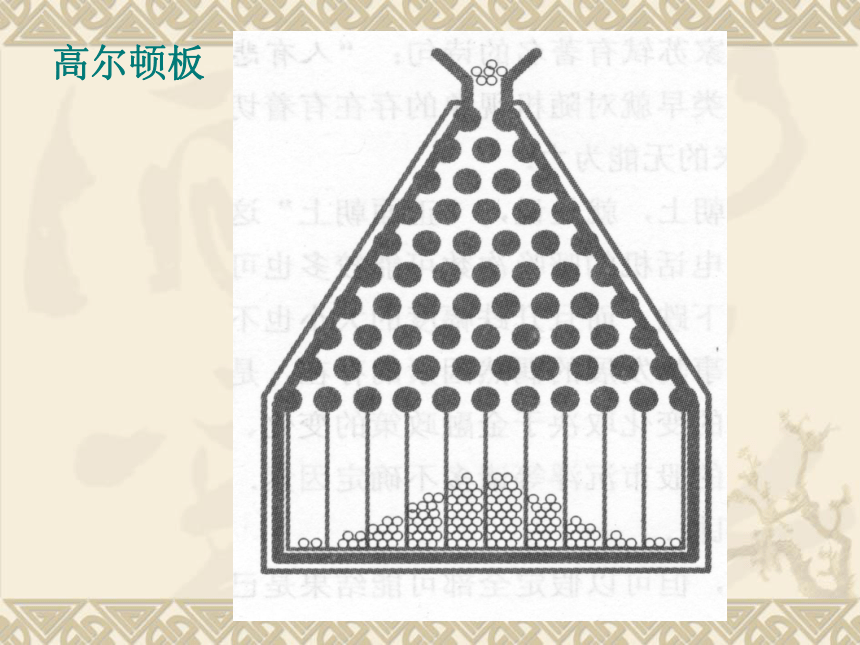
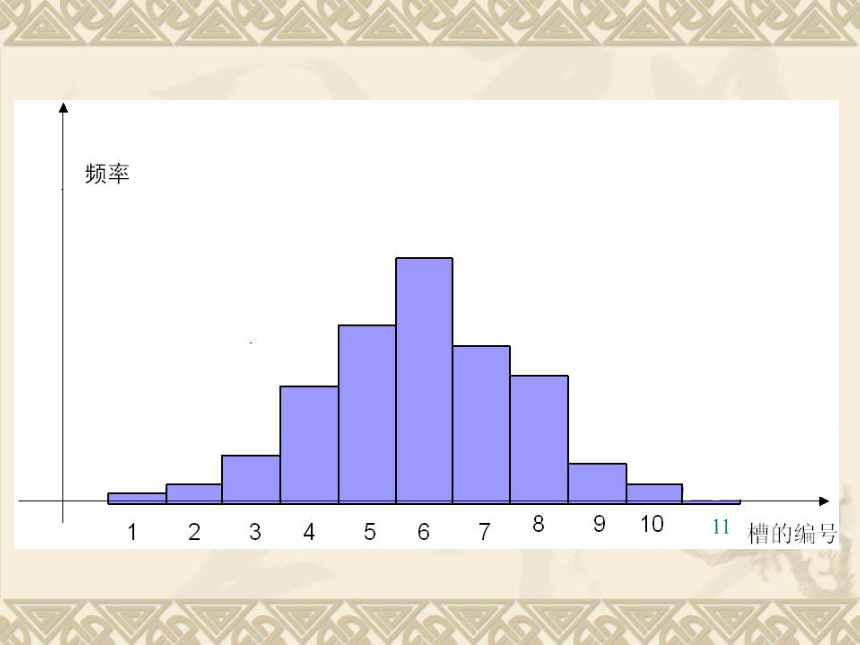
高尔顿板
11
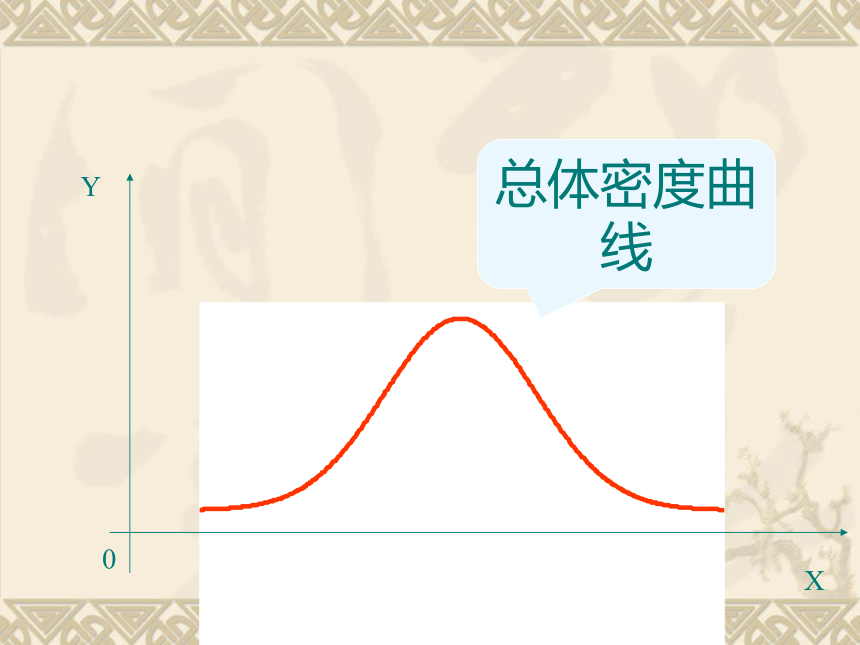
总体密度曲线
0
Y
X
导入
产品尺寸的总体密度曲线
就是或近似地是以下函数的图象：
1 、正态曲线的定义：
函数
式中的实数μ、σ(σ>0)是参数，分别表示
总体的平均数与标准差，称f( x)的图象称为正态曲线
c
d
a
b
平均数
X
Y
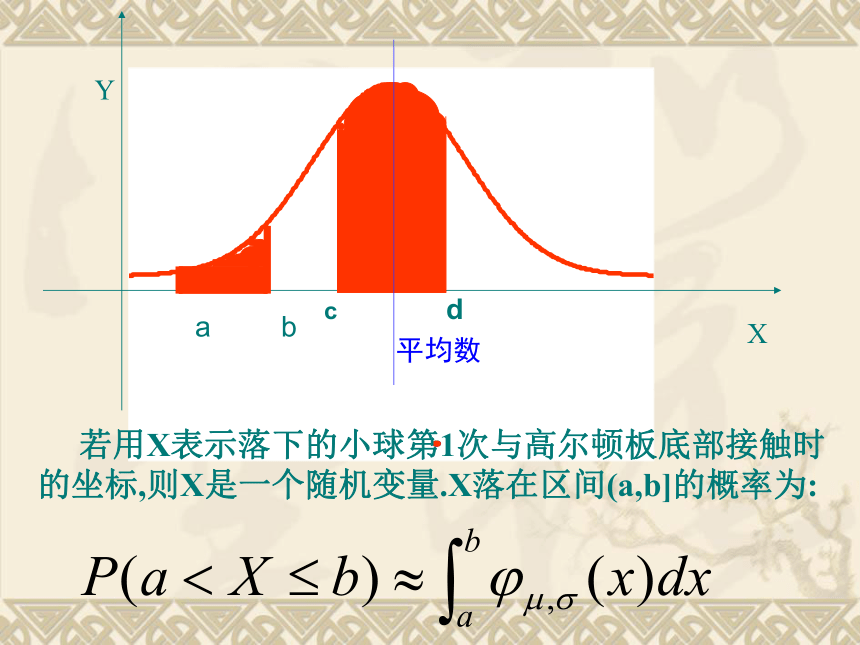
若用X表示落下的小球第1次与高尔顿板底部接触时的坐标,则X是一个随机变量.X落在区间(a,b]的概率为:
2.正态分布的定义:
如果对于任何实数 a则称为X 的正态分布. 正态分布由参数μ、σ唯一确定.正态分布记作N（ μ，σ2）.其图象称为正态曲线.
如果随机变量X服从正态分布，
则记作 X~ N（ μ，σ2）
在实际遇到的许多随机现象都服从或近似服从正态分布：
在生产中，在正常生产条件下各种产品的质量指标；
在测量中，测量结果；
在生物学中，同一群体的某一特征；……；
在气象中，某地每年七月份的平均气温、平均湿度
以及降雨量等，水文中的水位；
总之，正态分布广泛存在于自然界、生产及科学技术的许多领域中。
正态分布在概率和统计中占有重要地位。
m 的意义
产品
尺寸
(mm)
x1
x2
总体平均数反映总体随机变量的
平均水平
x3
x4
平均数
x= μ
产品
尺寸
(mm)
总体平均数反映总体随机变量的
平均水平
总体标准差反映总体随机变量的
集中与分散的程度
平均数
s的意义
正态总体的函数表示式
当μ= 0，σ=1时
标准正态总体的函数表示式
0
1
2
-1
-2
x
y
-3
3
μ=0
σ=1
标准正态曲线
μ
（－∞，μ]
（μ，+∞）
（1）当 = 时,函数值为最大.
(3) 的图象关于 对称.
（2） 的值域为
（4）当 ∈ 时 为增函数.
当 ∈ 时 为减函数.
0
1
2
-1
-2
x
y
-3
3
μ=0
σ=1
标准正态曲线
正态总体的函数表示式
=μ
例1、下列函数是正态密度函数的是（ ）
A.
B.
C.
D.
B
例2、标准正态总体的函数为
（1）证明f(x)是偶函数；
（2）求f(x)的最大值；
（3）利用指数函数的性质说明f(x)的增减性。
练习：
1、若一个正态分布的概率函数是一个偶函数且该函
数的最大值等于 ，求该正态分布的概率密度函数的解析式。
20
25
30
15
10
x
y
5
35
2、如图，是一个正态曲线，试根据图象写出其正态分布的概率密度函数的解析式，求出总体随机变量的期望和方差。
3、正态曲线的性质
0
1
2
-1
-2
x
y
-3
μ= -1
σ=0.5
0
1
2
-1
-2
x
y
-3
3
μ=0
σ=1
0
1
2
-1
-2
x
y
-3
3
4
μ=1
σ=2
具有两头低、中间高、左右对称的基本特征
0
1
2
-1
-2
x
y
-3
μ= -1
σ=0.5
0
1
2
-1
-2
x
y
-3
3
μ=0
σ=1
0
1
2
-1
-2
x
y
-3
3
4
μ=1
σ=2
（1）曲线在x轴的上方，与x轴不相交.
（2）曲线是单峰的,它关于直线x=μ对称.
3、正态曲线的性质
（4）曲线与x轴之间的面积为1
（3）曲线在x=μ处达到峰值(最高点)
方差相等、均数不等的正态分布图示
3
1
2
σ=0.5
μ=　-1
μ=0　
μ=　1
若 固定, 随 值的变化而沿x轴平移, 故 称为位置参数；
均数相等、方差不等的正态分布图示

=0.5
=1
=2
μ=0　
若 固定, 大时, 曲线矮而胖；
小时, 曲线瘦而高, 故称
为形状参数。
σ=0.5
0
1
2
-1
-2
x
y
-3
3
X=μ
σ=1
σ=2
(6)当μ一定时，曲线的形状由σ确定 .
σ越大，曲线越“矮胖”，表示总体的分布越分散；
σ越小，曲线越“瘦高”，表示总体的分布越集中.
（5）当 x<μ时,曲线上升;当x>μ时,曲线下降.并且当曲线向左、右两边无限延伸时,以x轴为渐近线,向它无限靠近.
3、正态曲线的性质
动画
例3、把一个正态曲线a沿着横轴方向向右移动2个单位，得到新的一条曲线b。下列说法中不正确的是（ ）
A.曲线b仍然是正态曲线；
B.曲线a和曲线b的最高点的纵坐标相等;
C.以曲线b为概率密度曲线的总体的期望比以曲线a为概率密度曲线的总体的期望大2;
D.以曲线b为概率密度曲线的总体的方差比以曲线a为概率密度曲线的总体的方差大2。
C
正态曲线下的面积规律
X轴与正态曲线所夹面积恒等于1 。
对称区域面积相等。
S(- ,-X)
S(X, )＝S(- ,-X)

正态曲线下的面积规律
对称区域面积相等。
S(-x1, -x2)
-x1 -x2 x2 x1
S(x1,x2)=S(-x2,-x1)

4、特殊区间的概率:
m-a
m+a
x=μ
若X~N ,则对于任何实数a>0,概率
为如图中的阴影部分的面积，对于固定的 和 而言，该面积随着 的减少而变大。这说明 越小, 落在区间 的概率越大，即X集中在 周围概率越大。
特别地有
我们从上图看到，正态总体在 以外取值的概率只有4.6％，在 以外取值的概率只有0.3 ％。
由于这些概率值很小（一般不超过5 ％ ），通常称这些情况发生为小概率事件。
例4、在某次数学考试中，考生的成绩 服从一个正态分布，即 ~N(90,100).
（1）试求考试成绩 位于区间(70,110)上的概率是多少？
（2）若这次考试共有2000名考生，试估计考试成绩在(80,100)间的考生大约有多少人？
练习：1、已知一次考试共有60名同学参加，考生的成绩X~ ，据此估计，大约应有57人的分数在下列哪个区间内？（ ）
(90,110] B. (95,125] C. (100,120] D.(105,115]
C
2、已知X~N (0,1)，则X在区间 内取值的概率等于（ ）
A.0.9544 B.0.0456 C.0.9772 D.0.0228
3、设离散型随机变量X~N(0,1),则 = ,
= .
4、若X~N(5,1),求P(6D
0.5
0.9544
2.4 正态分布(二)
高二数学 选修2-3
旧知回顾
函数
称f( x)的图象称为正态曲线。式中的
实数μ、σ(σ>0)是参数，分别表示
总体的平均数与标准差。
1 、正态曲线的定义：
x
y
2、标准正态总体的函数表示式
0
1
2
-1
-2
x
y
-3
3
μ=0
σ=1
3.正态分布的定义:
如果对于任何实数 a则称为X 为正态分布. 正态分布由参数μ、σ唯一确定.正态分布记作X~ N（ μ，σ2）.其图象称为正态曲线.如果随机变量X服从正态分布，则记作 X~ N（ μ，σ2）
a
b
X
Y
0
1
2
-1
-2
x
y
-3
μ= -1
σ=0.5
0
1
2
-1
-2
x
y
-3
3
μ=0
σ=1
0
1
2
-1
-2
x
y
-3
3
4
μ=1
σ=2
4、正态曲线的性质
（1）曲线在x轴的上方，与x轴不相交.
（2）曲线是单峰的,它关于直线x=μ对称.
（4）曲线与x轴之间的面积为1.
（3）曲线在x=μ处达到峰值(最高点)
（5）若 固定, 随 值的变化而沿x轴平移, 故 称为位置参数
（6）当μ一定时，曲线的形状由σ确定 .σ越大，曲线越“矮胖”，表示总体的分布越分散；σ越小，曲线越“瘦高”，表示总体的分布越集中.
练习：
一台机床生产一种尺寸为10mm的零件，现从中抽测10个，它们的尺寸分别如下（单位：mm）：10.2, 10.1, 10, 9.8, 9.9, 10.3, 9.7, 10, 9.9, 10.1.如果机床生产零件的尺寸 服从正态分布，求正态分布的概率密度函数式。
频率
组距
产品
尺寸
（mm）
a
b
若数据无限增多且组距无限缩小，那么频率分布直方图的顶边缩小乃至形成一条光滑的曲线，我们称此曲线为概率密度曲线．
总体在区间 内取值的概率
概率密度曲线
概率密度曲线的形状特征．
“中间高，两头低，
左右对称”
正态曲线下的面积规律
X轴与正态曲线所夹面积恒等于1 。
对称区域面积相等。
S(- ,-X)
S(X, )＝S(- ,-X)

正态曲线下的面积规律
对称区域面积相等。
S(-x1, -x2)
-x1 -x2 x2 x1
S(x1,x2)=S(-x2,-x1)

5、特殊区间的概率:
m-a
m+a
x=μ
若X~N ,则对于任何实数a>0,概率
为如图中的阴影部分的面积，对于固定的 和 而言，该面积随着 的减少而变大。这说明 越小, 落在区间 的概率越大，即X集中在 周围概率越大。
特别地有
我们从上图看到，正态总体在 以外取值的概率只有4.6％，在 以外取值的概率只有0.3 ％。
由于这些概率值很小（一般不超过5 ％ ），通常称这些情况发生为小概率事件。
区 间 取值概率
（μ－σ，μ＋σ] 68.3%
（μ－2σ，μ＋2σ] 95.4%
（μ－3σ，μ＋3σ] 99.7%
例1、在某次数学考试中，考生的成绩 服从一个正态分布，即 ~N(90,100).
（1）试求考试成绩 位于区间(70,110)上的概率是多少？
（2）若这次考试共有2000名考生，试估计考试成绩在(80,100)间的考生大约有多少人？
练习：1、已知一次考试共有60名同学参加，考生的成绩X~ ，据此估计，大约应有57人的分数在下列哪个区间内？（ ）
(90,110] B. (95,125] C. (100,120] D.(105,115]
C
2、已知X~N (0,1)，则X在区间 内取值的概率等于（ ）
A.0.9544 B.0.0456 C.0.9772 D.0.0228
3、设离散型随机变量X~N(0,1),则 = ,
= .
D
0.5
0.9544
4、若已知正态总体落在区间 的概率为0.5，则相应的正态曲线在x= 时达到最高点。
0.3
5、已知正态总体的数据落在（-3,-1）里的概率和落在（3,5）里的概率相等，那么这个正态总体的数学期望是 。
1
例3、若X~N(5,1),求P(6例2、已知 ，且 ，
则 等于( )
A.0.1 B. 0.2 C. 0.3 D.0.4
A
例4、如图，为某地成年男性体重的正态曲线图，请写出其正态分布密度函数，并求P（|X-72|<20）.
x
y
72(kg)
例5、某年级的一次信息技术测验成绩近似的服从正态分布 ，如果规定低于60分为不及格，求：
（1）成绩不及格的人数占多少？
（2）成绩在80~90内的学生占多少？