上海市浦东新区第四教育署2020-2021学年第一学期期末教学质量自主调研八年级数学试卷(Word版含答案)
文档属性
| 名称 | 上海市浦东新区第四教育署2020-2021学年第一学期期末教学质量自主调研八年级数学试卷(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-15 09:06:55 | ||
图片预览



文档简介
2020-2021学年度第一学期期末教学质量自主调研
八 年 级 数 学
一、单项选择题(本大题共有6 题,每题2 分,共12 分)∶
1.在下列式子中,表示y是x的正比例函数的是…………………………………………(
(A)y=√x (B)y=x?;
2.在下列方程中,有两个不相等实数根的是……………………………………………( )
(A)x?=2x-4;
(B)x2-4x+4=0;
(C)x?-2x-1=0;
(D)x2+4=0.
3.在下列二次根式中,与√ab(a>0,b>0)是同类二次根式的是……………( )
4.若正比例函数y=(2-k)x的图象经过第二、四象限,则k的取值范围是……( )
(A)k<-2; (B)k<2 (C)k >-2; (D)k>2
5.下列命题的逆命题是真命题的是…………………………………………………………()
(A)若a=b,则IaI=IbI
(B)同位角相等,两直线平行;
(C)对顶角相等;
(D)若a>0,b>0,则a+b>0.
6.在下列四个条件∶ ①AB?+BC?=AC?,②∠A=90°-∠B,③∠A=∠B=0.5∠C,
④∠A∶∠B∶∠C=5∶3∶2中,能确定AABC是直角三角形的条件有…( )
(A) ①③; (B)①②③; (C) ①②④; (D) ①②③④.
二、填空题(本大题共有 12 小题,每题3分,共36分)
7.若√1-X 有意义,那么x满足的条件是_______
8.计算∶ (√3)2+1=_
9.方程x2=x的解是
10.如果函数是正比例函数,那么m的值为_
11.如果反比例函数的图象经过点P(5,-2),那么在这个函数图象所在
的每个象限内,y的值随x的值增大而_______.(填"增大"或"减小")
12.某商店今年7月份的销售额是50万元,9月份的销售额是72万元,从7月份到9月
份,该店销售额平均每月的增长率是____
平面内到点 A的距离等于3 cm的点的轨迹是_____
在直角三角形中,两直角边长分别为6和8,则第三边上中线长是____.
已知点A(3,3),B(0,t),C(7,0),且AB=AC,则t=______
如图,DF垂直平分AB,EG垂直平分AC,若∠BAC=110°,则∠DAE=___°.
17.如图,在Rt△ABC中,∠C=90°,AB=10cm,BC=8cm,BD平分∠ABC,DE⊥AB,
垂足为E,则 DE=____cm.
18.如图,点P(a,a)是反比例函数在第一象限内的图象上的一个点,以点P为顶点作等边△PAB,使A、B落在 x轴上(点A在点B左侧),则△POA 的面积是____
三、简答题(本大题共7小题,第19、20题每题5分,第21、22题每题6分,第23题8分,第24题10 分,第25 题12 分,共 52 分)
20.解方程∶ 2x?+4x-7=0.
21.已知y与x+1成反比例,且当x=1时,y=2;
求∶当x= 0时,y的值.
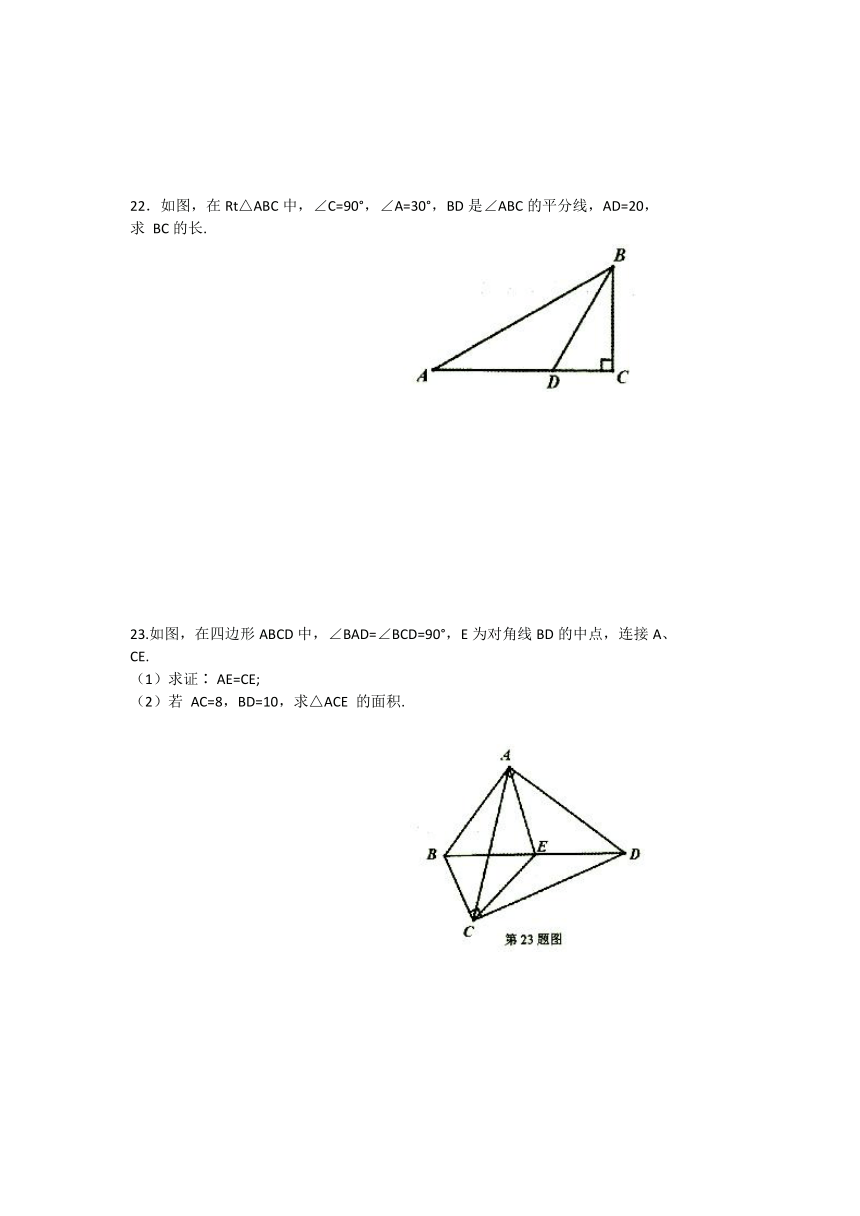
22.如图,在Rt△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,AD=20,
求 BC的长.
23.如图,在四边形ABCD中,∠BAD=∠BCD=90°,E为对角线BD的中点,连接A、
CE.
(1)求证∶ AE=CE;
(2)若 AC=8,BD=10,求△ACE 的面积.
如图,将一个长方形置在平面直角坐标系中,OA=2,OC=3,E是AB中点,反比例函数过点E且和BC相交点F
直接写出点B和点E的坐标
直线AB与反比例函数的解析式
连接OE、OF,求四边形OEBF的面积
25.已知∶在△ABC中,∠BAC=90°,AB=AC,点D为BC边上一动点(与点B不重合),连接AD,以AD始边作∠DAE=α(0°(1)如图一,当α=90°且AE=AD时,试说明CE和BD的位置关系和数量关系;
(2)如图二,当α=45°且点E在边BC上时,求证∶ BD2+CB?=DE2.
八 年 级 数 学
一、单项选择题(本大题共有6 题,每题2 分,共12 分)∶
1.在下列式子中,表示y是x的正比例函数的是…………………………………………(
(A)y=√x (B)y=x?;
2.在下列方程中,有两个不相等实数根的是……………………………………………( )
(A)x?=2x-4;
(B)x2-4x+4=0;
(C)x?-2x-1=0;
(D)x2+4=0.
3.在下列二次根式中,与√ab(a>0,b>0)是同类二次根式的是……………( )
4.若正比例函数y=(2-k)x的图象经过第二、四象限,则k的取值范围是……( )
(A)k<-2; (B)k<2 (C)k >-2; (D)k>2
5.下列命题的逆命题是真命题的是…………………………………………………………()
(A)若a=b,则IaI=IbI
(B)同位角相等,两直线平行;
(C)对顶角相等;
(D)若a>0,b>0,则a+b>0.
6.在下列四个条件∶ ①AB?+BC?=AC?,②∠A=90°-∠B,③∠A=∠B=0.5∠C,
④∠A∶∠B∶∠C=5∶3∶2中,能确定AABC是直角三角形的条件有…( )
(A) ①③; (B)①②③; (C) ①②④; (D) ①②③④.
二、填空题(本大题共有 12 小题,每题3分,共36分)
7.若√1-X 有意义,那么x满足的条件是_______
8.计算∶ (√3)2+1=_
9.方程x2=x的解是
10.如果函数是正比例函数,那么m的值为_
11.如果反比例函数的图象经过点P(5,-2),那么在这个函数图象所在
的每个象限内,y的值随x的值增大而_______.(填"增大"或"减小")
12.某商店今年7月份的销售额是50万元,9月份的销售额是72万元,从7月份到9月
份,该店销售额平均每月的增长率是____
平面内到点 A的距离等于3 cm的点的轨迹是_____
在直角三角形中,两直角边长分别为6和8,则第三边上中线长是____.
已知点A(3,3),B(0,t),C(7,0),且AB=AC,则t=______
如图,DF垂直平分AB,EG垂直平分AC,若∠BAC=110°,则∠DAE=___°.
17.如图,在Rt△ABC中,∠C=90°,AB=10cm,BC=8cm,BD平分∠ABC,DE⊥AB,
垂足为E,则 DE=____cm.
18.如图,点P(a,a)是反比例函数在第一象限内的图象上的一个点,以点P为顶点作等边△PAB,使A、B落在 x轴上(点A在点B左侧),则△POA 的面积是____
三、简答题(本大题共7小题,第19、20题每题5分,第21、22题每题6分,第23题8分,第24题10 分,第25 题12 分,共 52 分)
20.解方程∶ 2x?+4x-7=0.
21.已知y与x+1成反比例,且当x=1时,y=2;
求∶当x= 0时,y的值.
22.如图,在Rt△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,AD=20,
求 BC的长.
23.如图,在四边形ABCD中,∠BAD=∠BCD=90°,E为对角线BD的中点,连接A、
CE.
(1)求证∶ AE=CE;
(2)若 AC=8,BD=10,求△ACE 的面积.
如图,将一个长方形置在平面直角坐标系中,OA=2,OC=3,E是AB中点,反比例函数过点E且和BC相交点F
直接写出点B和点E的坐标
直线AB与反比例函数的解析式
连接OE、OF,求四边形OEBF的面积
25.已知∶在△ABC中,∠BAC=90°,AB=AC,点D为BC边上一动点(与点B不重合),连接AD,以AD始边作∠DAE=α(0°
(2)如图二,当α=45°且点E在边BC上时,求证∶ BD2+CB?=DE2.
同课章节目录
