华东师大版(2012)七年级下册 6.3实践与探索(第2课时)课件(共16张ppt)
文档属性
| 名称 | 华东师大版(2012)七年级下册 6.3实践与探索(第2课时)课件(共16张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 263.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-15 11:18:41 | ||
图片预览






文档简介
6.3探 索 与 实 践
(第2课时)
学习目标
(1)弄清商品利润问题中“售价:、“进价”、“利润”三者之间
的关系,以及“标价”和“售价”的区分。
(2)会用“列表分析”的方法解决实际问题,使同学们体会到认真
分析后,抽丝剥茧得到答案的成就感。
(3)掌握列方程解应用题的规范格式。
一、商品利润问题:
分析:
等量关系:
标价的90%(即售价)-成本=7
若设这种服装每件在成本是x元,那么:
每件服装的标价为:
每件服装的实际售价为:
每件服装的利润为:
由等量关系,列出方程为:
例1、 一家药店将某种医用口罩按成本价提高50%后标价,
又以9折(即按标价的90% )优惠卖出,结果每个仍获利7元,
那么这种医用口罩的成本是多少元?
大家想一想,这7元的利润是怎么来的?
(1+50%)x?90%
(1+50%)x?90%-x
(1+50%)x?90%-x=7
解:设这种服装每件的成本是x元,根据题意,得
解这个方程,得 x=20
经检验,符合题意
答;这种医用口罩的成本是20元 。
整理规范
其中,“根据题意,得”、
“经检验,符合题意”,是我们
规范答题的基本语言。
(1+50%)x?90%-x=7
例1、 一家药店将某种医用口罩按成本价提高50%后标价,
又以9折(即按标价的90% )优惠卖出,结果每个仍获利7元,
那么这种医用口罩的成本是多少元?
跟踪训练:
练习1:一批红外线测温仪按成本价提高30%后标价,后因疫情的关系,按标价的8折,每件260元卖出,这批红外线测温仪每件的成本价是多少元?
等量关系:标价的八折=260
解:设这批夹克每件的成本价是x元,根据题意,得
解这个方程,得 x=250
答;这批红外线测温仪每件的成本价是250元 。
经检验,符合题意
练习2:某商场销售一款空调每台的标价是 1635元,在一次促销活动中,若按标价的八折销售,仍可盈利9%,则这款空调每台的进价为多少元?
等量关系:售价(标价的八折)-进价=利润(进价的9%)
解:设这款空调每台的进价为x元,根据题意,得
解这个方程,得 x=1200
经检验,符合题意
答;这款空调每台的进价为1200元。
跟踪训练:
请同学们认真思考:
“仍可盈利9%”,是指仍
可盈利谁的9%
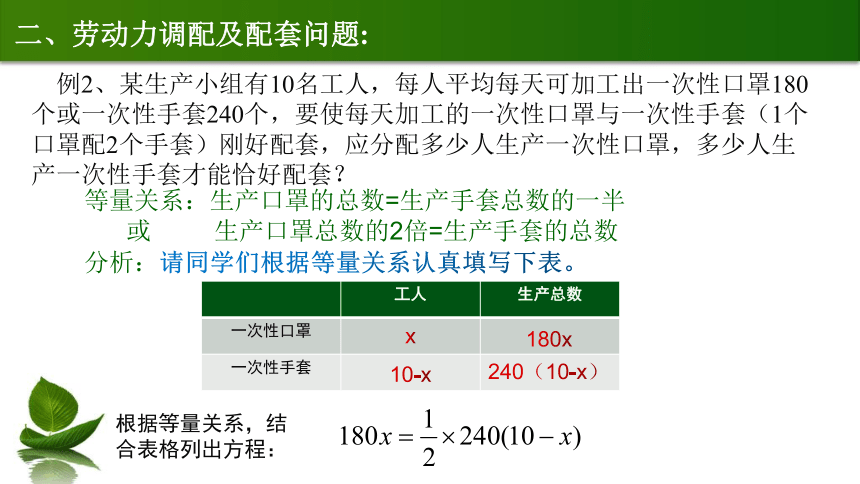
二、劳动力调配及配套问题:
等量关系:生产口罩的总数=生产手套总数的一半
或 生产口罩总数的2倍=生产手套的总数
分析:请同学们根据等量关系认真填写下表。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
工人
生产总数
一次性口罩
一次性手套
x
10-x
180x
240(10-x)
根据等量关系,结合表格列出方程:
例2、某生产小组有10名工人,每人平均每天可加工出一次性口罩180个或一次性手套240个,要使每天加工的一次性口罩与一次性手套(1个口罩配2个手套)刚好配套,应分配多少人生产一次性口罩,多少人生产一次性手套才能恰好配套?
整理规范
例2、某生产小组有10名工人,每人平均每天可加工出一次性口罩180个或一次性手套240个,要使每天加工的一次性口罩与一次性手套(1个口罩配2个手套)刚好配套,应分配多少人生产一次性口罩,多少人生产一次性手套才能恰好配套?
解:设分配x人加一次性口罩,根据题意,得
解这个方程,得 x=4
经检验,符合题意
10-x=10-4=6
答;应分配4人生产一次性口罩,6人生产一次性手套才能恰好配套。
跟踪训练:
练习3:留山制衣厂某车间计划用十天时间加工一批童装和成人装共360件,该车间每天能加工童装45件或成人装30件,问该车间应安排几天生产童装,几天生产成人装,才能如期完成任务?
等量关系:童装总件数+成人装总件数=360
分析:请同学们根据等量关系认真填写下表,并规范解答。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
安排天数
生产总数
童装
成人装
x
10-x
45x
30(10-x)
整理规范
练习3:留山制衣厂某车间计划用十天时间加工一批童装和成人装共360件,该车间每天能加工童装45件或成人装30件,问该车间应安排几天生产童装,几天生产成人装,才能如期完成任务?
解:设安排x天生产童装,根据题意,得
解这个方程,得 x=4
经检验,符合题意
10-x=10-4=6
答;应安排4天生产童装,6天生产成人装,才能如期完成任务。
真题训练:
(2015南召县期中测试改编):南召县为支援武汉准备制做一批某种型号的防护服,已知防护材料每3米可做上衣2件或裤子3条(一件上衣和一条裤子为一套),现计划用6000米长的这种材料做防护服,应分别用多少米做上衣,多少米做裤子,才能恰好配套?
等量关系:做上衣的总件数=做裤子的总件数
分析:请同学们根据等量关系认真填写下表,并规范解答。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
用料
包含几个3米
总件数
上衣
裤子
x
6000-x
观察这两个式
子是否符合代
数式的书写规
范?
整理规范
(2015南召县期中测试改编):南召县为支援武汉准备制做一批某种型号的防护服,已知防护材料每3米可做上衣2件或裤子3条(一件上衣和一条裤子为一套),现计划用6000米长的这种材料做防护服,应分别用多少米做上衣,多少米做裤子,才能恰好配套?
解:设用x米做上衣,根据题意,得
解这个方程,得 x=3600
经检验,符合题意
6000-x=6000-3600=2400
答;应用3600米做上衣,2400米做裤子,才能恰好配套。
(1)在解决“商品利润问题”时,大多数等量关系都是“售价-进价=利润“,但一定要分清“标价”和“售价”两者之间的关系,其次题目中出现“仍可盈利a%”指的是仍可获得成本的a%,
本节小结
(2)在解决“劳动力调配及配套问题”时,最好的做法就是“列表分析”,一点点分析并用代数式表示出来,结合等量关系列出方程。
以上两个问题是考试过程中的高频考点,希望同学们独立思考,认真对待。
课后作业
1、一件商品按成本价提高20%后标价,又以9折出售,售价为27元,
则这个商品的成本价是多少元?
2、某商店把彩色电视机按标价的九折出售,仍可获利20%,已知
该彩电的进价为2400元,则标价是多少元?
3、孟氏服装厂加工一种休闲上衣,一个工人平均每天可加工15件
上衣(无袖子)或10个袖子,若车间共有80人,则应如何分配工人
才能使每天加工的休闲上衣都是成品?
自我反思
没有足够的自律,所谓的天赋
不堪一击!
再见
(第2课时)
学习目标
(1)弄清商品利润问题中“售价:、“进价”、“利润”三者之间
的关系,以及“标价”和“售价”的区分。
(2)会用“列表分析”的方法解决实际问题,使同学们体会到认真
分析后,抽丝剥茧得到答案的成就感。
(3)掌握列方程解应用题的规范格式。
一、商品利润问题:
分析:
等量关系:
标价的90%(即售价)-成本=7
若设这种服装每件在成本是x元,那么:
每件服装的标价为:
每件服装的实际售价为:
每件服装的利润为:
由等量关系,列出方程为:
例1、 一家药店将某种医用口罩按成本价提高50%后标价,
又以9折(即按标价的90% )优惠卖出,结果每个仍获利7元,
那么这种医用口罩的成本是多少元?
大家想一想,这7元的利润是怎么来的?
(1+50%)x?90%
(1+50%)x?90%-x
(1+50%)x?90%-x=7
解:设这种服装每件的成本是x元,根据题意,得
解这个方程,得 x=20
经检验,符合题意
答;这种医用口罩的成本是20元 。
整理规范
其中,“根据题意,得”、
“经检验,符合题意”,是我们
规范答题的基本语言。
(1+50%)x?90%-x=7
例1、 一家药店将某种医用口罩按成本价提高50%后标价,
又以9折(即按标价的90% )优惠卖出,结果每个仍获利7元,
那么这种医用口罩的成本是多少元?
跟踪训练:
练习1:一批红外线测温仪按成本价提高30%后标价,后因疫情的关系,按标价的8折,每件260元卖出,这批红外线测温仪每件的成本价是多少元?
等量关系:标价的八折=260
解:设这批夹克每件的成本价是x元,根据题意,得
解这个方程,得 x=250
答;这批红外线测温仪每件的成本价是250元 。
经检验,符合题意
练习2:某商场销售一款空调每台的标价是 1635元,在一次促销活动中,若按标价的八折销售,仍可盈利9%,则这款空调每台的进价为多少元?
等量关系:售价(标价的八折)-进价=利润(进价的9%)
解:设这款空调每台的进价为x元,根据题意,得
解这个方程,得 x=1200
经检验,符合题意
答;这款空调每台的进价为1200元。
跟踪训练:
请同学们认真思考:
“仍可盈利9%”,是指仍
可盈利谁的9%
二、劳动力调配及配套问题:
等量关系:生产口罩的总数=生产手套总数的一半
或 生产口罩总数的2倍=生产手套的总数
分析:请同学们根据等量关系认真填写下表。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
工人
生产总数
一次性口罩
一次性手套
x
10-x
180x
240(10-x)
根据等量关系,结合表格列出方程:
例2、某生产小组有10名工人,每人平均每天可加工出一次性口罩180个或一次性手套240个,要使每天加工的一次性口罩与一次性手套(1个口罩配2个手套)刚好配套,应分配多少人生产一次性口罩,多少人生产一次性手套才能恰好配套?
整理规范
例2、某生产小组有10名工人,每人平均每天可加工出一次性口罩180个或一次性手套240个,要使每天加工的一次性口罩与一次性手套(1个口罩配2个手套)刚好配套,应分配多少人生产一次性口罩,多少人生产一次性手套才能恰好配套?
解:设分配x人加一次性口罩,根据题意,得
解这个方程,得 x=4
经检验,符合题意
10-x=10-4=6
答;应分配4人生产一次性口罩,6人生产一次性手套才能恰好配套。
跟踪训练:
练习3:留山制衣厂某车间计划用十天时间加工一批童装和成人装共360件,该车间每天能加工童装45件或成人装30件,问该车间应安排几天生产童装,几天生产成人装,才能如期完成任务?
等量关系:童装总件数+成人装总件数=360
分析:请同学们根据等量关系认真填写下表,并规范解答。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
安排天数
生产总数
童装
成人装
x
10-x
45x
30(10-x)
整理规范
练习3:留山制衣厂某车间计划用十天时间加工一批童装和成人装共360件,该车间每天能加工童装45件或成人装30件,问该车间应安排几天生产童装,几天生产成人装,才能如期完成任务?
解:设安排x天生产童装,根据题意,得
解这个方程,得 x=4
经检验,符合题意
10-x=10-4=6
答;应安排4天生产童装,6天生产成人装,才能如期完成任务。
真题训练:
(2015南召县期中测试改编):南召县为支援武汉准备制做一批某种型号的防护服,已知防护材料每3米可做上衣2件或裤子3条(一件上衣和一条裤子为一套),现计划用6000米长的这种材料做防护服,应分别用多少米做上衣,多少米做裤子,才能恰好配套?
等量关系:做上衣的总件数=做裤子的总件数
分析:请同学们根据等量关系认真填写下表,并规范解答。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
用料
包含几个3米
总件数
上衣
裤子
x
6000-x
观察这两个式
子是否符合代
数式的书写规
范?
整理规范
(2015南召县期中测试改编):南召县为支援武汉准备制做一批某种型号的防护服,已知防护材料每3米可做上衣2件或裤子3条(一件上衣和一条裤子为一套),现计划用6000米长的这种材料做防护服,应分别用多少米做上衣,多少米做裤子,才能恰好配套?
解:设用x米做上衣,根据题意,得
解这个方程,得 x=3600
经检验,符合题意
6000-x=6000-3600=2400
答;应用3600米做上衣,2400米做裤子,才能恰好配套。
(1)在解决“商品利润问题”时,大多数等量关系都是“售价-进价=利润“,但一定要分清“标价”和“售价”两者之间的关系,其次题目中出现“仍可盈利a%”指的是仍可获得成本的a%,
本节小结
(2)在解决“劳动力调配及配套问题”时,最好的做法就是“列表分析”,一点点分析并用代数式表示出来,结合等量关系列出方程。
以上两个问题是考试过程中的高频考点,希望同学们独立思考,认真对待。
课后作业
1、一件商品按成本价提高20%后标价,又以9折出售,售价为27元,
则这个商品的成本价是多少元?
2、某商店把彩色电视机按标价的九折出售,仍可获利20%,已知
该彩电的进价为2400元,则标价是多少元?
3、孟氏服装厂加工一种休闲上衣,一个工人平均每天可加工15件
上衣(无袖子)或10个袖子,若车间共有80人,则应如何分配工人
才能使每天加工的休闲上衣都是成品?
自我反思
没有足够的自律,所谓的天赋
不堪一击!
再见
