华东师大版八年级下册数学16.1.1从分数到分式课件 (共23张)
文档属性
| 名称 | 华东师大版八年级下册数学16.1.1从分数到分式课件 (共23张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-15 00:00:00 | ||
图片预览







文档简介
学习目标
1、理解分式的概念,会根据概念判断一个式子是不是分式。
2、掌握分式有(无)意义的条件,会求分式有(无)意义时字母的取值范围。
3、会求分式值为零的条件。
温故知新
1、单项式的概念?
数字与字母的乘积
2、多项式的概念?
由几个单项式相加或相减连接而成的式子
3、( )和( )统称为整式
单项式
多项式
1、将1个苹果,平均分给2个同学,每个人分得
2、将2个苹果,平均分给3个同学,每个人分得
4、将1个苹果,平均分给n个同学,每个人分得
5、将1个苹果,平均分给n+2个同学,每个人分得
6、将2个苹果,平均分给m+n个同学,每个人分得
7、将n个苹果,平均分给x+y个同学,每个人分得
3、将n个苹果,平均分给4个同学,每个人分得
类比引路·以旧换新
同学们发现这一类式子:
它们有什么共同特征?
并且分母中含字母
n
n+2
m+n
x+y
共同特征:都是 的形式
类比引路·以旧换新
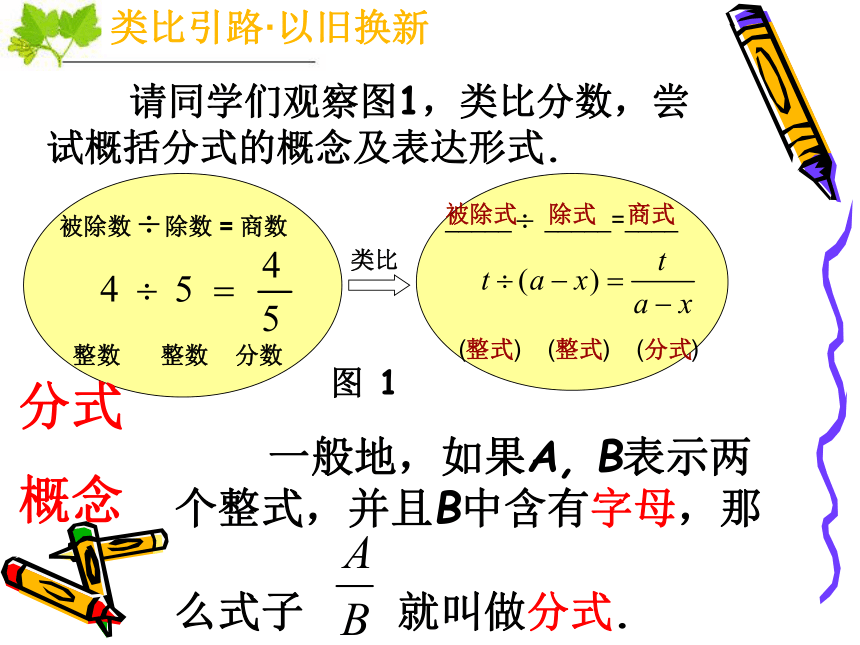
请同学们观察图1,类比分数,尝试概括分式的概念及表达形式.
被除数 除数 = 商数
整数 整数 分数
类比
_____ _____=____
( ) ( ) ( )
图 1
被除式 除式 商式
整式 整式 分式
分式
概念
一般地,如果A, B表示两个整式,并且B中含有字母,那
么式子 就叫做分式.
2、下列式子中,哪些是分式?哪些是整式?两类式子的区别是什么?
分式与整式的区别就在于分母中是否含字母.
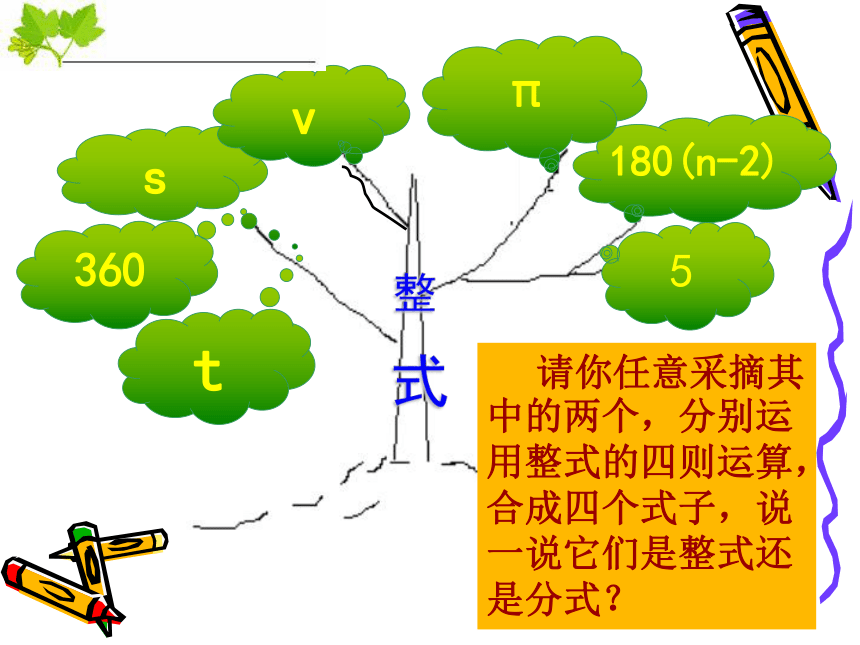
s
180(n-2)
5
整 式
π
v
360
t
请你任意采摘其中的两个,分别运用整式的四则运算,合成四个式子,说一说它们是整式还是分式?
思考: 分式 中的分母应满足什么条件,分式有意义?
分母不能为0,即B不能为0
∴当 B≠0 时,分式 才有意义。
例题学习
(1)当x 时,分式 有意义;
(2)当x 时,分式 有意义;
(3)当b 时,分式 有意义.
例 1 填空:
分母 3x≠0, 即 x≠0
分母 x-1≠0,
即 x≠1
分母 5-3b≠0 ,即 b≠
一展身手
当字母满足什么条件时,下列分式有意义?
a为任意实数
思考: 分式 应满足什么条件,分式的值为零?
分子为0,且分母不能为0
∴A=0且B≠0 时,分式 =0
试求下列字母为何值时,分式的值为0?
(1)解:若使分式的值为0,则有
?
?
由?得x=-1
由?得
你能顺利完成吗?
分式的概念
分式值为0
分式无意义
分式
分式有意义
继续探索……
2、本节的思想方法
1、本节思路
(2)分类的思想
(1)类比的思想
1
2
3
4
5
6
7
某村有n个人,耕地40公顷,人均耕地面积为 公顷;
感悟·应用
它是分式吗
1
我能行
感悟·应用
当 ______时,分式 有意义.
≠2
2
我能行
我能行
感悟·应用
判断
3
我能行
感悟·应用
当 _____时,分式 的值为0.
=0
4
X=( )分式 的值为0
5
-2
m 分式 无意义
=5
6
我能行
感悟·应用
7
分式与整式的区别是什么?
看分母是否含有字母
1、理解分式的概念,会根据概念判断一个式子是不是分式。
2、掌握分式有(无)意义的条件,会求分式有(无)意义时字母的取值范围。
3、会求分式值为零的条件。
温故知新
1、单项式的概念?
数字与字母的乘积
2、多项式的概念?
由几个单项式相加或相减连接而成的式子
3、( )和( )统称为整式
单项式
多项式
1、将1个苹果,平均分给2个同学,每个人分得
2、将2个苹果,平均分给3个同学,每个人分得
4、将1个苹果,平均分给n个同学,每个人分得
5、将1个苹果,平均分给n+2个同学,每个人分得
6、将2个苹果,平均分给m+n个同学,每个人分得
7、将n个苹果,平均分给x+y个同学,每个人分得
3、将n个苹果,平均分给4个同学,每个人分得
类比引路·以旧换新
同学们发现这一类式子:
它们有什么共同特征?
并且分母中含字母
n
n+2
m+n
x+y
共同特征:都是 的形式
类比引路·以旧换新
请同学们观察图1,类比分数,尝试概括分式的概念及表达形式.
被除数 除数 = 商数
整数 整数 分数
类比
_____ _____=____
( ) ( ) ( )
图 1
被除式 除式 商式
整式 整式 分式
分式
概念
一般地,如果A, B表示两个整式,并且B中含有字母,那
么式子 就叫做分式.
2、下列式子中,哪些是分式?哪些是整式?两类式子的区别是什么?
分式与整式的区别就在于分母中是否含字母.
s
180(n-2)
5
整 式
π
v
360
t
请你任意采摘其中的两个,分别运用整式的四则运算,合成四个式子,说一说它们是整式还是分式?
思考: 分式 中的分母应满足什么条件,分式有意义?
分母不能为0,即B不能为0
∴当 B≠0 时,分式 才有意义。
例题学习
(1)当x 时,分式 有意义;
(2)当x 时,分式 有意义;
(3)当b 时,分式 有意义.
例 1 填空:
分母 3x≠0, 即 x≠0
分母 x-1≠0,
即 x≠1
分母 5-3b≠0 ,即 b≠
一展身手
当字母满足什么条件时,下列分式有意义?
a为任意实数
思考: 分式 应满足什么条件,分式的值为零?
分子为0,且分母不能为0
∴A=0且B≠0 时,分式 =0
试求下列字母为何值时,分式的值为0?
(1)解:若使分式的值为0,则有
?
?
由?得x=-1
由?得
你能顺利完成吗?
分式的概念
分式值为0
分式无意义
分式
分式有意义
继续探索……
2、本节的思想方法
1、本节思路
(2)分类的思想
(1)类比的思想
1
2
3
4
5
6
7
某村有n个人,耕地40公顷,人均耕地面积为 公顷;
感悟·应用
它是分式吗
1
我能行
感悟·应用
当 ______时,分式 有意义.
≠2
2
我能行
我能行
感悟·应用
判断
3
我能行
感悟·应用
当 _____时,分式 的值为0.
=0
4
X=( )分式 的值为0
5
-2
m 分式 无意义
=5
6
我能行
感悟·应用
7
分式与整式的区别是什么?
看分母是否含有字母
