华东师大版八年级下册数学17.2.1《平面直角坐标系》 课件 (共25张PPT)
文档属性
| 名称 | 华东师大版八年级下册数学17.2.1《平面直角坐标系》 课件 (共25张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-15 11:52:16 | ||
图片预览






文档简介
第17章 函数及其图象
17.2函数的图象
17.2.1 平面直角坐标系
华东师大版 八年级下册
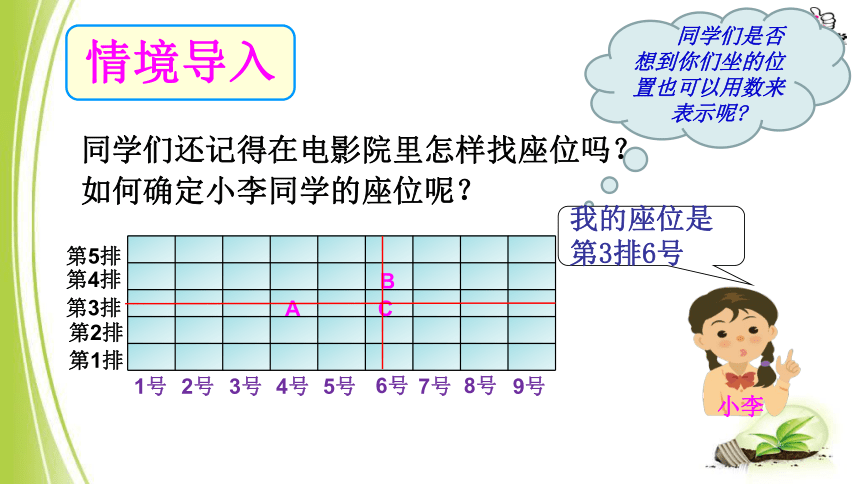
情境导入
同学们是否想到你们坐的位置也可以用数来表示呢?
同学们还记得在电影院里怎样找座位吗?
如何确定小李同学的座位呢?
我的座位是第3排6号
第5排
第4排
第3排
第2排
第1排
1号
2号
3号
4号
5号
6号
7号
8号
9号
C
小李
A
B
情境导入
1.理解平面直角坐标系的有关概念,会正确建立平面直角坐标系,能根据坐标描出点的位置,由点的位置写出坐标;(重点)
2.了解象限的划分,掌握各象限内及坐标轴上点的坐标的特征.(难点)
学习目标
自主学习(1)
思考:x轴与y轴上的点属于哪个象限?
内容:阅读课本34页最后一段和35页第二段内容
时间:5分钟
要求:
1.思考:如何在平面内建立直角坐标系?
2.在课本162页方格图上建立平面直角坐标系,并指出坐标系各部分的名称(x轴、y轴、原点及第一、二、三、四象限).
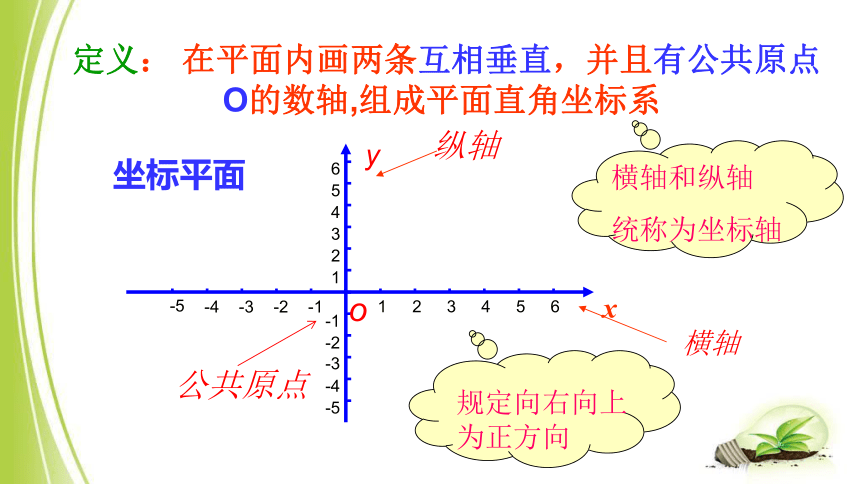
定义: 在平面内画两条互相垂直,并且有公共原点 O的数轴,组成平面直角坐标系
坐标平面
纵轴
横轴
横轴和纵轴
统称为坐标轴
1
2
3
4
5
6
-1
-2
-3
-4
-5
1
2
3
4
5
6
-1
-2
-3
-4
-5
o
x
y
公共原点
规定向右向上为正方向
1
2
3
4
5
6
-1
-2
-3
-4
-5
y
1
2
3
4
5
6
-1
-2
-3
-4
-5
x
o
第二象限
第三象限
第四象限
第一象限
坐标平面的划分:
注意:象限以数轴为界,
坐标轴上的点不属于任何象限。
M
四个象限,两条坐标轴
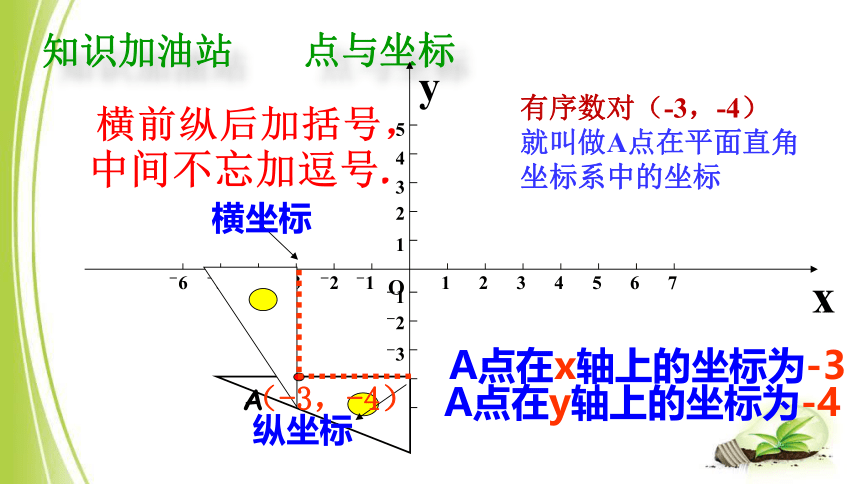
知识加油站
点与坐标
1
2
3
4
5
6
7
1
2
3
4
5
y
O
1
1
5
2
4
6
3
2
3
4
5
x
A
横坐标
纵坐标
A点在x轴上的坐标为-3
A点在y轴上的坐标为-4
(-3,-4)
有序数对(-3,-4)
就叫做A点在平面直角
坐标系中的坐标
小游戏: 我在哪?
游戏规则:以班长为原点,班长所在的排为x轴,所在的列为y轴,建立平面直角坐标系。
请在卡片上写下自己的坐标!
1.平面直角坐标系的建立
在平面内画两条原点重合、互相垂直且具有相同单位长度的数轴,就建立了平面直角坐标系.
在平面直角坐标系中,两条坐标轴把平面分四个区域,分别称为第一、二、三、四象限,坐标轴上的点不属于任何一个象限.
???????笛卡尔,法国数学家、科学家和哲学家。早在1637年以前,他受到了经纬度的启发。(地理上的经纬度是以赤道和本初子午线为标准的,这两条线从局部上看可以看成平面内互相垂直的两条线.)发明了平面直角坐标系,又称笛卡尔坐标系。
笛卡尔(1596-1660)
阅读材料
自主学习(2)
思考:如果知道点的坐标,如A(-4,-3),你能在直角坐标系内描出该点吗?
要求:阅读课本35页第一段内容
时间:3分钟
思考:
在平面直角坐标系内,怎样找已知点的坐标?
2.由点找坐标、由坐标描点
·P
·
A
点P的坐标为(3,2)
(1)如图,写出点P的坐标;
(2)在下图中描出点A(-4,-3)
有序实数对----先横后纵
大家一起来做游戏
3、请坐标是(2,1)、(-1,1)
(-1,-1)、(1,2)的同学起立。
每位同学表示平面内的一个点,老师点一人为原点,建立直角坐标系, 横向的同学表示x轴,纵向的同学表示y轴.
1、请说出自己所表示的点所在的象限.
2、请说出自己所表示的点的坐标.
D
1.写出下图中的多边形ABCDEF各个顶点的坐标,并说出各顶点所在的象限或坐标轴.
-1
-2
1
3
-1
-3
【答案】
A(-2,0)在x轴上
B(0,-3)在y轴上
C(3,-3)在第四象限
D(4,0)在x轴上
E(3,3)在第一象限
F(0,3)在y轴上
B
C
E
F
1
2
3
4
-2
2
O
A
y
x
试一试
2. 在平面直角坐标系中分别描出点P(3,2)、Q(2,3) 、S(-1,4) 、R(4,-1).
观察:P(3,2)与Q(2,3)是同一个点吗?
S(-1,4)与R(4,-1)是同一个点吗?
这里得到的结果告诉我们什么?
试一试
平面直角坐标系内的点和有序实数对是一一对应的。
写出点A,B,C,D,E,F的坐标.
F
·
合作探究
观察各点坐标,
思考:
(1)在四个象限内点的坐标各有什么特征?
(2)两条坐标轴上的点的坐标各有什么特征?
【答案】
A(3,3)
B(-5,2)
C(-4,-3)
D(4,-3)
E(5,0)
F(0,-2)
归纳
点的位置
横坐标的
符号
纵坐标的
符号
第一象限
第二象限
第三象限
第四象限
点的位置
横坐标的
符号
纵坐标的
符号
在x轴的正半轴上
在x轴的负半轴上
在y轴的正半轴上
在y轴的负半轴上
+
-
0
1.平面直角坐标系中原点坐标是 ,
在y 轴上的点的横坐标是_____,在x轴上的点的纵坐标是______.
2.若点P(a,b)在第三象限,则a 0,b 0.
若点P(a,b)在第四象限,则a 0,b 0.
3.点 M(- 5,3)在第 象限,到x轴的距离是___,到y轴的距离是___ .
巩固练习
4设点M(x,y)在第二象限,且|x|=2,|y|=3,则点M的坐标是( )
A.(2,3) B.(3,-2) C.(-2,3) D.(2,-3)
(0,0)
0
0
<
<
<
>
3
5
C
二
5. 在平面直角坐标系中,已知点P 在第四象限,距离x 轴3个单位长度, 距离y 轴4个单位长度,则点P 的坐标为 .
6.点A(m+3,m+1)在x轴上,求A点的坐标.
(4,-3)
解:因为点A在x轴上
所以 m+1=0
即 m=-1
所以点A的坐标为(2,0)
则 m+3=-1+3=2
本节课你学到了什么?
还有什么疑惑?
课堂小结
课堂小结
1.如何建立平面直角坐标系?
在平面内画两条原点重合、互相垂直且具有相同单位长度的数轴,就建立了平面直角坐标系.
2.象限的划分 3.x轴与y轴上的点不属于任何象限
x轴上所有点的纵坐标都为0;
y轴上所有点的横坐标都为0.
4.平面直角坐标系内的点与有序实数对
一一对应.
5.点到x轴的距离等于纵坐标的绝对值;
点到y轴的距离等于横坐标的绝对值.
( ,+)
(+,+)
(+, )
( , )
3. 如何由点的位置确定点的坐标
1. 如何建立平面直角坐标系
5. 知道象限内极坐标轴上点的坐标的特点
2. 平面直角坐标系各部分的名称是什么?
4. 如何根据坐标描出点的位置
作业
教材课后练习1、2、3题
我们愈是学习,愈觉得自己的贫乏。 —— 雪莱
17.2函数的图象
17.2.1 平面直角坐标系
华东师大版 八年级下册
情境导入
同学们是否想到你们坐的位置也可以用数来表示呢?
同学们还记得在电影院里怎样找座位吗?
如何确定小李同学的座位呢?
我的座位是第3排6号
第5排
第4排
第3排
第2排
第1排
1号
2号
3号
4号
5号
6号
7号
8号
9号
C
小李
A
B
情境导入
1.理解平面直角坐标系的有关概念,会正确建立平面直角坐标系,能根据坐标描出点的位置,由点的位置写出坐标;(重点)
2.了解象限的划分,掌握各象限内及坐标轴上点的坐标的特征.(难点)
学习目标
自主学习(1)
思考:x轴与y轴上的点属于哪个象限?
内容:阅读课本34页最后一段和35页第二段内容
时间:5分钟
要求:
1.思考:如何在平面内建立直角坐标系?
2.在课本162页方格图上建立平面直角坐标系,并指出坐标系各部分的名称(x轴、y轴、原点及第一、二、三、四象限).
定义: 在平面内画两条互相垂直,并且有公共原点 O的数轴,组成平面直角坐标系
坐标平面
纵轴
横轴
横轴和纵轴
统称为坐标轴
1
2
3
4
5
6
-1
-2
-3
-4
-5
1
2
3
4
5
6
-1
-2
-3
-4
-5
o
x
y
公共原点
规定向右向上为正方向
1
2
3
4
5
6
-1
-2
-3
-4
-5
y
1
2
3
4
5
6
-1
-2
-3
-4
-5
x
o
第二象限
第三象限
第四象限
第一象限
坐标平面的划分:
注意:象限以数轴为界,
坐标轴上的点不属于任何象限。
M
四个象限,两条坐标轴
知识加油站
点与坐标
1
2
3
4
5
6
7
1
2
3
4
5
y
O
1
1
5
2
4
6
3
2
3
4
5
x
A
横坐标
纵坐标
A点在x轴上的坐标为-3
A点在y轴上的坐标为-4
(-3,-4)
有序数对(-3,-4)
就叫做A点在平面直角
坐标系中的坐标
小游戏: 我在哪?
游戏规则:以班长为原点,班长所在的排为x轴,所在的列为y轴,建立平面直角坐标系。
请在卡片上写下自己的坐标!
1.平面直角坐标系的建立
在平面内画两条原点重合、互相垂直且具有相同单位长度的数轴,就建立了平面直角坐标系.
在平面直角坐标系中,两条坐标轴把平面分四个区域,分别称为第一、二、三、四象限,坐标轴上的点不属于任何一个象限.
???????笛卡尔,法国数学家、科学家和哲学家。早在1637年以前,他受到了经纬度的启发。(地理上的经纬度是以赤道和本初子午线为标准的,这两条线从局部上看可以看成平面内互相垂直的两条线.)发明了平面直角坐标系,又称笛卡尔坐标系。
笛卡尔(1596-1660)
阅读材料
自主学习(2)
思考:如果知道点的坐标,如A(-4,-3),你能在直角坐标系内描出该点吗?
要求:阅读课本35页第一段内容
时间:3分钟
思考:
在平面直角坐标系内,怎样找已知点的坐标?
2.由点找坐标、由坐标描点
·P
·
A
点P的坐标为(3,2)
(1)如图,写出点P的坐标;
(2)在下图中描出点A(-4,-3)
有序实数对----先横后纵
大家一起来做游戏
3、请坐标是(2,1)、(-1,1)
(-1,-1)、(1,2)的同学起立。
每位同学表示平面内的一个点,老师点一人为原点,建立直角坐标系, 横向的同学表示x轴,纵向的同学表示y轴.
1、请说出自己所表示的点所在的象限.
2、请说出自己所表示的点的坐标.
D
1.写出下图中的多边形ABCDEF各个顶点的坐标,并说出各顶点所在的象限或坐标轴.
-1
-2
1
3
-1
-3
【答案】
A(-2,0)在x轴上
B(0,-3)在y轴上
C(3,-3)在第四象限
D(4,0)在x轴上
E(3,3)在第一象限
F(0,3)在y轴上
B
C
E
F
1
2
3
4
-2
2
O
A
y
x
试一试
2. 在平面直角坐标系中分别描出点P(3,2)、Q(2,3) 、S(-1,4) 、R(4,-1).
观察:P(3,2)与Q(2,3)是同一个点吗?
S(-1,4)与R(4,-1)是同一个点吗?
这里得到的结果告诉我们什么?
试一试
平面直角坐标系内的点和有序实数对是一一对应的。
写出点A,B,C,D,E,F的坐标.
F
·
合作探究
观察各点坐标,
思考:
(1)在四个象限内点的坐标各有什么特征?
(2)两条坐标轴上的点的坐标各有什么特征?
【答案】
A(3,3)
B(-5,2)
C(-4,-3)
D(4,-3)
E(5,0)
F(0,-2)
归纳
点的位置
横坐标的
符号
纵坐标的
符号
第一象限
第二象限
第三象限
第四象限
点的位置
横坐标的
符号
纵坐标的
符号
在x轴的正半轴上
在x轴的负半轴上
在y轴的正半轴上
在y轴的负半轴上
+
-
0
1.平面直角坐标系中原点坐标是 ,
在y 轴上的点的横坐标是_____,在x轴上的点的纵坐标是______.
2.若点P(a,b)在第三象限,则a 0,b 0.
若点P(a,b)在第四象限,则a 0,b 0.
3.点 M(- 5,3)在第 象限,到x轴的距离是___,到y轴的距离是___ .
巩固练习
4设点M(x,y)在第二象限,且|x|=2,|y|=3,则点M的坐标是( )
A.(2,3) B.(3,-2) C.(-2,3) D.(2,-3)
(0,0)
0
0
<
<
<
>
3
5
C
二
5. 在平面直角坐标系中,已知点P 在第四象限,距离x 轴3个单位长度, 距离y 轴4个单位长度,则点P 的坐标为 .
6.点A(m+3,m+1)在x轴上,求A点的坐标.
(4,-3)
解:因为点A在x轴上
所以 m+1=0
即 m=-1
所以点A的坐标为(2,0)
则 m+3=-1+3=2
本节课你学到了什么?
还有什么疑惑?
课堂小结
课堂小结
1.如何建立平面直角坐标系?
在平面内画两条原点重合、互相垂直且具有相同单位长度的数轴,就建立了平面直角坐标系.
2.象限的划分 3.x轴与y轴上的点不属于任何象限
x轴上所有点的纵坐标都为0;
y轴上所有点的横坐标都为0.
4.平面直角坐标系内的点与有序实数对
一一对应.
5.点到x轴的距离等于纵坐标的绝对值;
点到y轴的距离等于横坐标的绝对值.
( ,+)
(+,+)
(+, )
( , )
3. 如何由点的位置确定点的坐标
1. 如何建立平面直角坐标系
5. 知道象限内极坐标轴上点的坐标的特点
2. 平面直角坐标系各部分的名称是什么?
4. 如何根据坐标描出点的位置
作业
教材课后练习1、2、3题
我们愈是学习,愈觉得自己的贫乏。 —— 雪莱
