华东师大版七年级下册数学 6.2.1《等式的性质与方程的简单变形》课件 (共34张PPT)
文档属性
| 名称 | 华东师大版七年级下册数学 6.2.1《等式的性质与方程的简单变形》课件 (共34张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 834.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-15 00:00:00 | ||
图片预览



文档简介
第三章
一元一次方程
3.1
从算式到方程
3.1.2
等式的性质
√
√
√
√
√
观察下列各式,有什么发现?
;
;
;④
3;
;⑥2+3=5;⑦3×4=12;⑧9x+10=19;
;
.
用等号表示相等关系的式子叫做等式.
我们可以用
a=b表示一般的等式.
b
右
左
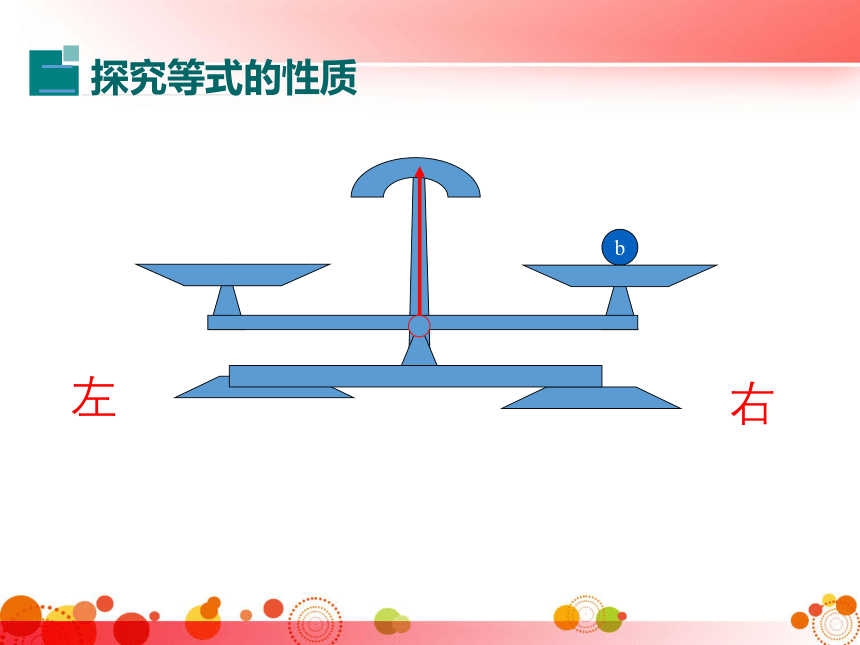
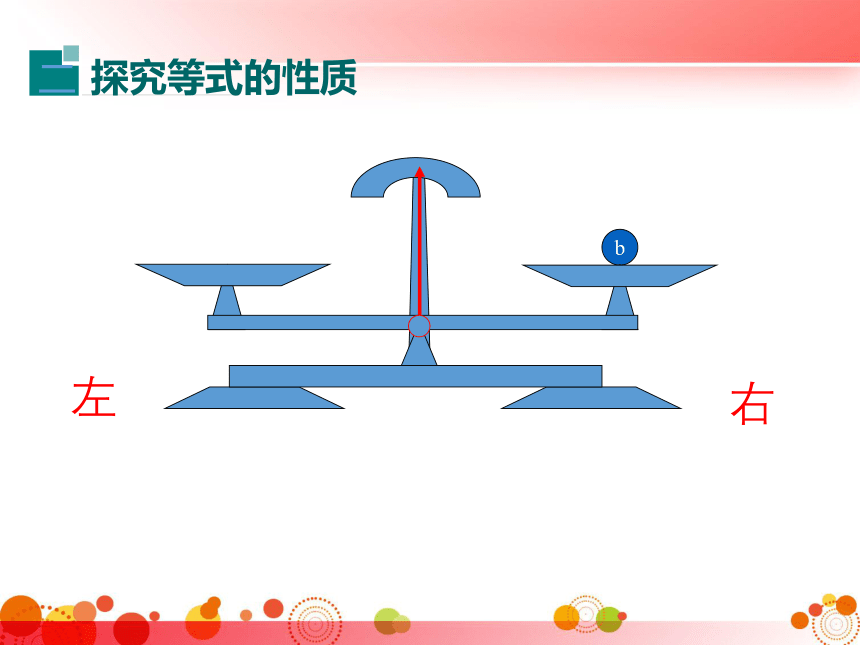
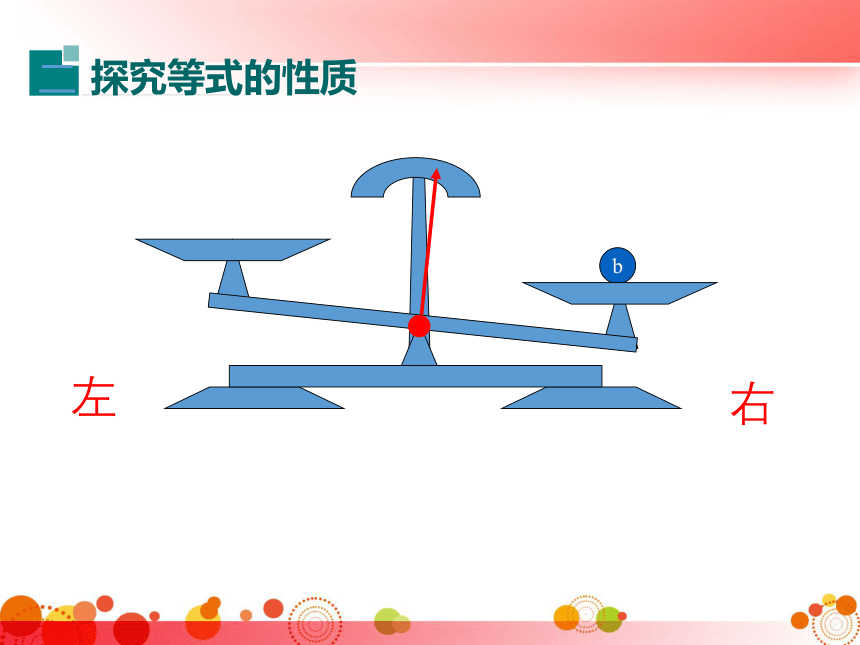
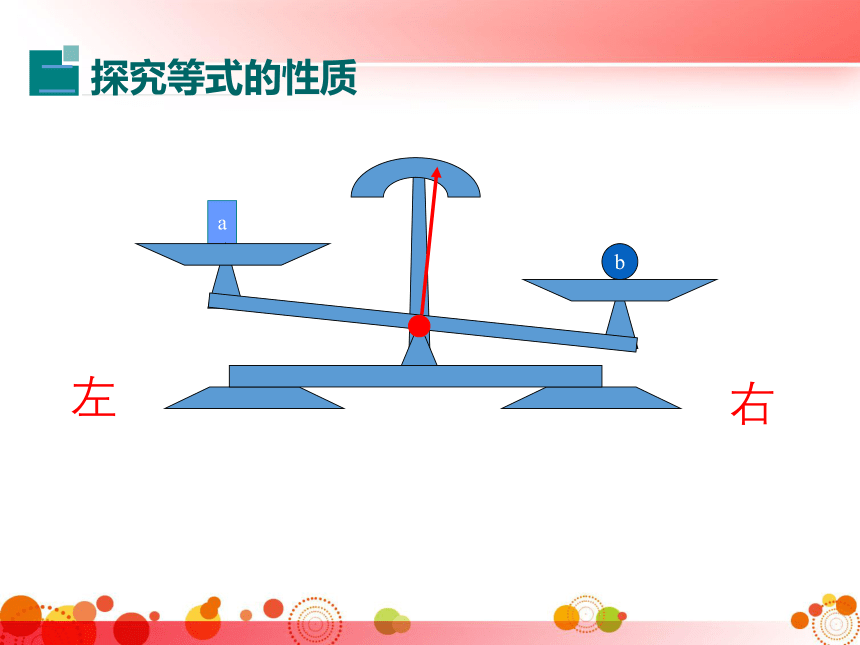
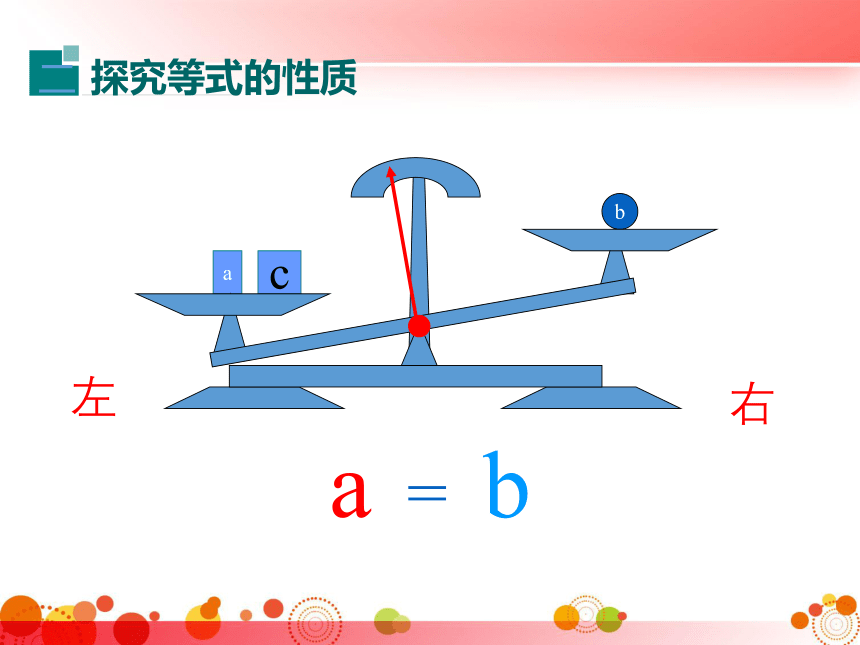
探究等式的性质
二
b
右
左
探究等式的性质
二
b
右
左
探究等式的性质
二
b
a
右
左
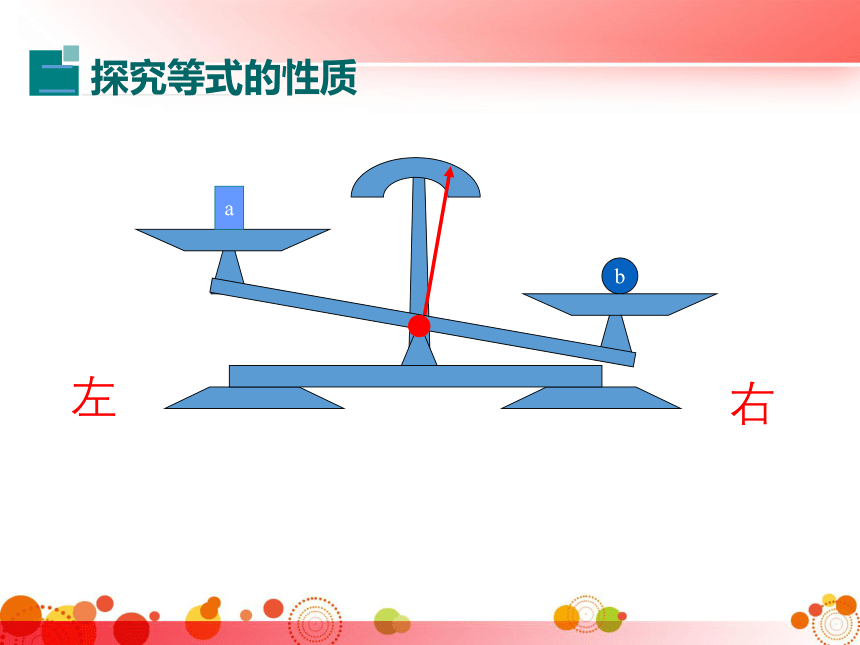
探究等式的性质
二
a
b
右
左
探究等式的性质
二
a
b
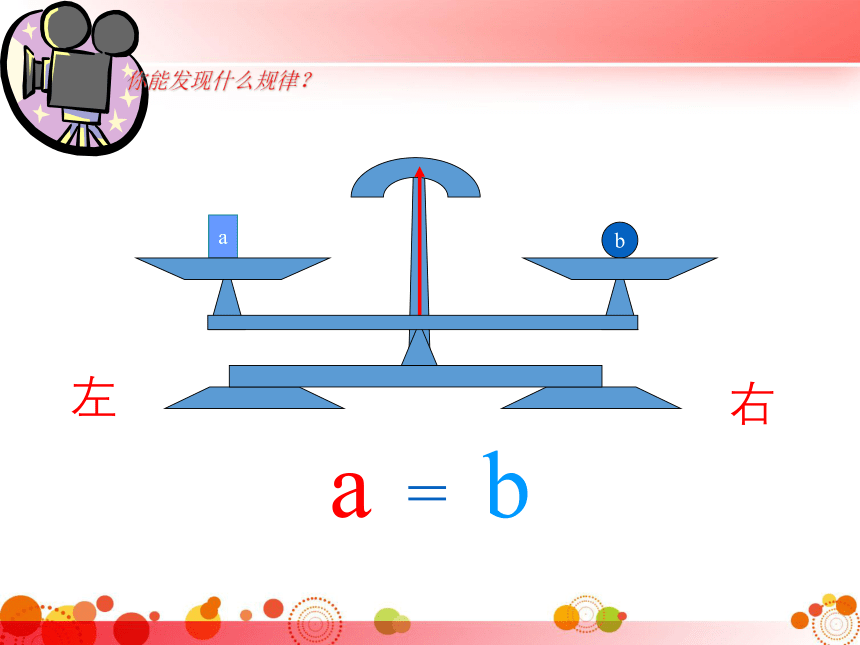
你能发现什么规律?
a
=
b
右
左
a
b
a
=
b
c
右
左
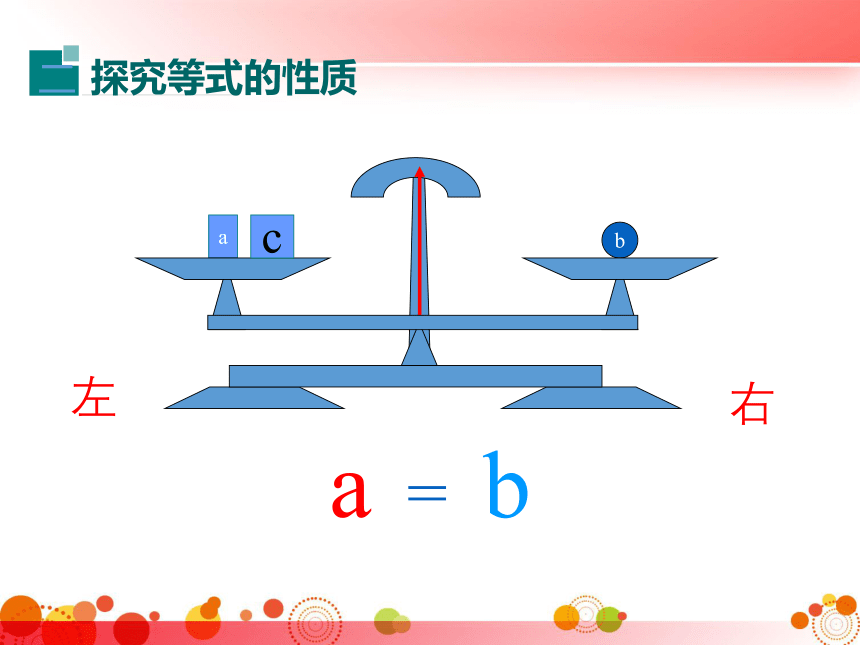
探究等式的性质
二
c
a
b
a
=
b
右
左
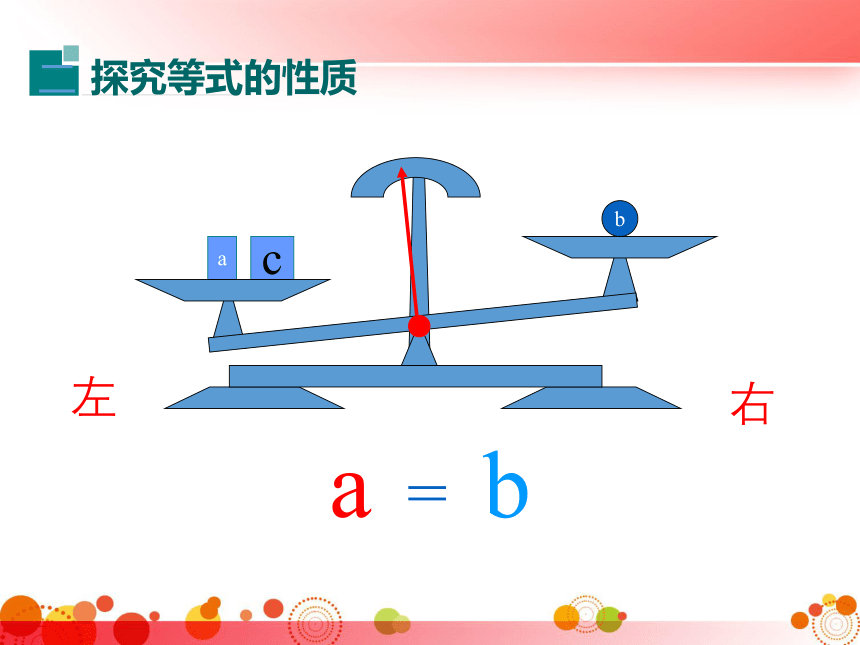
探究等式的性质
二
b
c
a
a
=
b
右
左
探究等式的性质
二
c
a
c
b
a
=
b
右
左
探究等式的性质
二
c
a
c
b
你能发现什么规律?
a
=
b
a+c
b+c
=
右
左
c
c
a
=
b
b
a
右
左
探究等式的性质
二
c
a
=
b
b
a
右
左
探究等式的性质
二
c
a
=
b
b
a
右
左
探究等式的性质
二
a
=
b
a
b
右
左
你能发现什么规律?
a
=
b
a-c
b-c
=
a
b
右
左
等式的性质1:等式的两边加(或减)同一个数(或式子),结果仍相等.
a
b
a
=
b
右
左
探究等式的性质
二
a
b
a
=
b
右
左
b
a
2a
=
2b
探究等式的性质
二
a
b
a
=
b
右
左
a
a
b
b
3a
=
3b
探究等式的性质
二
a
b
a
=
b
右
左
a
a
a
a
a
a
b
b
b
b
b
b
C个
C个
ac
=
bc
探究等式的性质
二
a
b
a
=
b
右
左
等式的性质2:等式的两边乘同一个数,或除以同一个不为0的数,结果仍相等.
(2)
怎样从等式
3+x=1
得到等式
x
=-2?
(3)
怎样从等式
4x=12
得到等式
x
=3?
依据等式的性质1两边同时减3.
依据等式的性质2两边同时除以4或同乘
.
依据等式的性质2两边同时除以
或同乘100.
例1
(1)
怎样从等式
x-5=
y-5
得到等式
x
=
y
?
依据等式的性质1两边同时加5.
典例精析
(4)
怎样从等式
得到等式
a
=
b?
利用等式的性质解方程
二
例3
利用等式的性质解下列方程:
(1)
x
+
7
=
26
解:
得
方程两边同时减去7,
x
+
7
=
26
-7
-7
于是
=
x
19
小结:解一元一次方程要“化归”为“
x=a
”的形式.
两边同时除以-5,
得
解:
方程
(2)
-5x
=
20
思考:为使
(2)
中未知项的系数化为1,将要用到等式的什么性质
?
化简,得
x=-4
-5x÷(-5)=
20
÷(-5)
解:方程两边同时加上5,得
化简,得
方程两边同时
乘
-3,
得
x
=
-27
x=-27是原方程的解吗?
思考:对比(1),(3)有什么新特点
?
(3)
针对训练:
(1)
x+6
=
17
;
(2)
-3x
=
15
;
(4)
(3)
2x-1
=
-3
;
解:(1)两边同时减去6,得x=11.
(2)两边同时除以-3,得x=-5.
(3)两边同时加上1,得2x=-2.
两边同时除以2,得x=-1.
(4)两边同时加上-1,得
两边同时乘以-3,得x=9.
当堂练习
A
2.
下列各式变形正确的是
(
)
A.
由3x-1=
2x+1得3x-2x
=1+1
B.
由5+1=
6得5=
6+1
C.
由2(x+1)
=
2y+1得x
+1=
y
+1
D.
由2a
+
3b
=
c-6
得2a
=
c-18b
1.
下列说法正确的是_______
A.
等式都是方程
B.
方程都是等式
C.
不是方程的就不是等式
D.
未知数的值就是方程的解
B
3.
下列变形,正确的是
(
)
A.
若ac
=
bc,则a
=
b
B.
若
,则a
=
b
C.
若a2
=
b2,则a
=
b
D.
若
,则x
=
-2
B
五、拓展练习
练习:将3x=8x两边同时除以x,得3=8.对其中的错误,
四名同学归纳如下:
同学甲:方程本身是错的.
同学乙:方程无解.
同学丙:3x比8x小.
同学丁:不能两边除以x,因为x有可能等于0.
你有什么看法?与同学交流.
课堂小结
等式的
基本性质
基本性质1
基本性质2
应用
如果a=b,那么a±c=b±c.
如果a=b,那么ac=bc;
如果a=b(c≠0),那么
.
运用等式的性质把方程“化归”为最简的形式
x
=
a
一元一次方程
3.1
从算式到方程
3.1.2
等式的性质
√
√
√
√
√
观察下列各式,有什么发现?
;
;
;④
3;
;⑥2+3=5;⑦3×4=12;⑧9x+10=19;
;
.
用等号表示相等关系的式子叫做等式.
我们可以用
a=b表示一般的等式.
b
右
左
探究等式的性质
二
b
右
左
探究等式的性质
二
b
右
左
探究等式的性质
二
b
a
右
左
探究等式的性质
二
a
b
右
左
探究等式的性质
二
a
b
你能发现什么规律?
a
=
b
右
左
a
b
a
=
b
c
右
左
探究等式的性质
二
c
a
b
a
=
b
右
左
探究等式的性质
二
b
c
a
a
=
b
右
左
探究等式的性质
二
c
a
c
b
a
=
b
右
左
探究等式的性质
二
c
a
c
b
你能发现什么规律?
a
=
b
a+c
b+c
=
右
左
c
c
a
=
b
b
a
右
左
探究等式的性质
二
c
a
=
b
b
a
右
左
探究等式的性质
二
c
a
=
b
b
a
右
左
探究等式的性质
二
a
=
b
a
b
右
左
你能发现什么规律?
a
=
b
a-c
b-c
=
a
b
右
左
等式的性质1:等式的两边加(或减)同一个数(或式子),结果仍相等.
a
b
a
=
b
右
左
探究等式的性质
二
a
b
a
=
b
右
左
b
a
2a
=
2b
探究等式的性质
二
a
b
a
=
b
右
左
a
a
b
b
3a
=
3b
探究等式的性质
二
a
b
a
=
b
右
左
a
a
a
a
a
a
b
b
b
b
b
b
C个
C个
ac
=
bc
探究等式的性质
二
a
b
a
=
b
右
左
等式的性质2:等式的两边乘同一个数,或除以同一个不为0的数,结果仍相等.
(2)
怎样从等式
3+x=1
得到等式
x
=-2?
(3)
怎样从等式
4x=12
得到等式
x
=3?
依据等式的性质1两边同时减3.
依据等式的性质2两边同时除以4或同乘
.
依据等式的性质2两边同时除以
或同乘100.
例1
(1)
怎样从等式
x-5=
y-5
得到等式
x
=
y
?
依据等式的性质1两边同时加5.
典例精析
(4)
怎样从等式
得到等式
a
=
b?
利用等式的性质解方程
二
例3
利用等式的性质解下列方程:
(1)
x
+
7
=
26
解:
得
方程两边同时减去7,
x
+
7
=
26
-7
-7
于是
=
x
19
小结:解一元一次方程要“化归”为“
x=a
”的形式.
两边同时除以-5,
得
解:
方程
(2)
-5x
=
20
思考:为使
(2)
中未知项的系数化为1,将要用到等式的什么性质
?
化简,得
x=-4
-5x÷(-5)=
20
÷(-5)
解:方程两边同时加上5,得
化简,得
方程两边同时
乘
-3,
得
x
=
-27
x=-27是原方程的解吗?
思考:对比(1),(3)有什么新特点
?
(3)
针对训练:
(1)
x+6
=
17
;
(2)
-3x
=
15
;
(4)
(3)
2x-1
=
-3
;
解:(1)两边同时减去6,得x=11.
(2)两边同时除以-3,得x=-5.
(3)两边同时加上1,得2x=-2.
两边同时除以2,得x=-1.
(4)两边同时加上-1,得
两边同时乘以-3,得x=9.
当堂练习
A
2.
下列各式变形正确的是
(
)
A.
由3x-1=
2x+1得3x-2x
=1+1
B.
由5+1=
6得5=
6+1
C.
由2(x+1)
=
2y+1得x
+1=
y
+1
D.
由2a
+
3b
=
c-6
得2a
=
c-18b
1.
下列说法正确的是_______
A.
等式都是方程
B.
方程都是等式
C.
不是方程的就不是等式
D.
未知数的值就是方程的解
B
3.
下列变形,正确的是
(
)
A.
若ac
=
bc,则a
=
b
B.
若
,则a
=
b
C.
若a2
=
b2,则a
=
b
D.
若
,则x
=
-2
B
五、拓展练习
练习:将3x=8x两边同时除以x,得3=8.对其中的错误,
四名同学归纳如下:
同学甲:方程本身是错的.
同学乙:方程无解.
同学丙:3x比8x小.
同学丁:不能两边除以x,因为x有可能等于0.
你有什么看法?与同学交流.
课堂小结
等式的
基本性质
基本性质1
基本性质2
应用
如果a=b,那么a±c=b±c.
如果a=b,那么ac=bc;
如果a=b(c≠0),那么
.
运用等式的性质把方程“化归”为最简的形式
x
=
a
