华东师大版数学七年级下册课件:8.2.2.不等式的简单变形(共23张)
文档属性
| 名称 | 华东师大版数学七年级下册课件:8.2.2.不等式的简单变形(共23张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 458.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-15 00:00:00 | ||
图片预览







文档简介
2. 不等式的简单变形
等式有哪些性质?
(1)等式的两边都加上(或减去)同一个数或同一个整式,所得的结果仍是等式.
若 a = b,则 a + c = b + c(或 a – c = b – c)
(2)等式的两边都乘以(或除以)同一个数(除数不能为零),所得的结果仍是等式.
若 a = b,则 ac = bc(或 ,c ≠ 0)
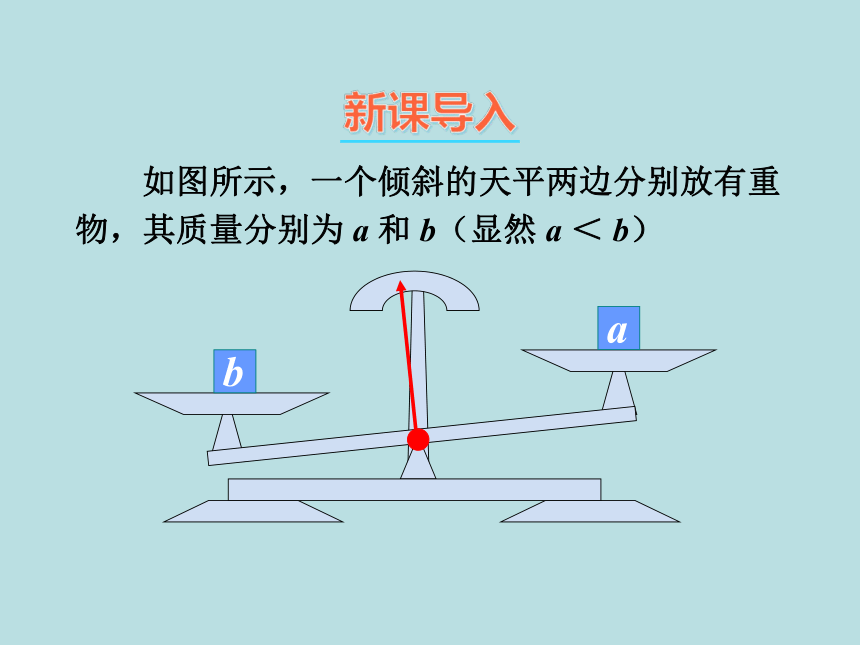
如图所示,一个倾斜的天平两边分别放有重物,其质量分别为 a 和 b(显然 a < b)
b
a
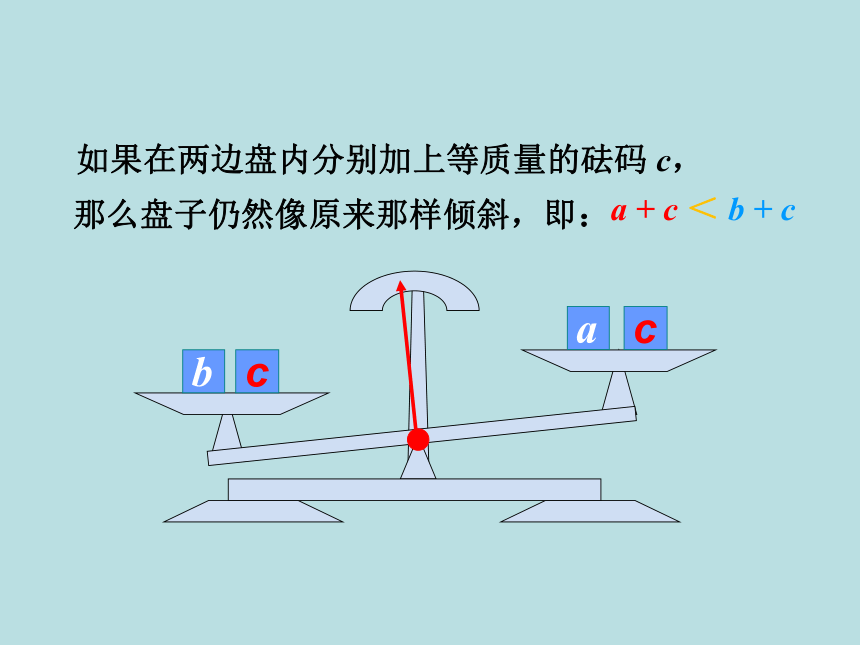
如果在两边盘内分别加上等质量的砝码 c,
b
a
c
c
那么盘子仍然像原来那样倾斜,即:
a + c < b + c
概括
不等式的性质 1 如果 a > b,那么
a + c > b + c,a – c > b – c
这就是说,不等式的两边都加上(或都减去)同一个数或同一个整式,不等号的方向不变.
思考
不等式的两边都乘以(或都除以)同一个不为零的数,不等号的方向是否也不变呢?
试一试
将不等式 7 > 4 的两边都乘以同一个数,比较所得结果的大小,用“<”、“>”或“=”号填空:
7×3 __ 4×3
7×2 __ 4×2
7÷ 5 __ 4÷5
7÷ 7 __ 4÷7
发现:不等式的两边都乘以(或除以)同一个正数,不等号的方向不变.
>
>
>
>
试一试
将不等式 7 > 4 的两边都乘以同一个数,比较所得结果的大小,用“<”、“>”或“=”号填空:
7×(– 3)__ 4×(– 3)
7×( – 2)__ 4×(– 2)
7 ÷( – 4)__ 4÷(– 4)
7 ÷( – 7)__ 4÷(– 7)
<
<
<
<
发现:不等式的两边都乘以(或除以)同一个负数,不等号的方向 改变 .
概括
不等式的性质 2 如果 a>b,并且 c>0,那么
不等式的性质 3 如果 a>b,并且 c<0,那么
这就是说,不等式的两边都乘以(或都除以)同一个正数,不等号的方向不变;不等式的两边都乘以(或都除以)同一个负数,不等号的方向改变.
例 1 解不等式:
(1)x – 7 < 8 ; (2)3x < 2x – 3.
解(1)不等式的两边都加上 7,不等号的方向不变,所以
x – 7 + 7 < 8 + 7
得 x < 15.
例 1 解不等式:
(1)x – 7 < 8 ; (2)3x < 2x – 3 .
解(2)不等式的两边都减去 2x(即都加上 – 2x),不等号的方向不变,所以
3x – 2x < 2x – 3 – 2x
得 x< – 3.
试总结一下:怎样进行不等式的“移项”?
例 2 解不等式:
(1) ; (2)﹣2x < 6.
解(1)不等式的两边都乘以 2,不等号的方向不变,所以
得 x > ﹣6.
例 2 解不等式:
(1) ; (2)– 2x < 6.
解(2)不等式的两边都除以 – 2(即都乘以 ),不等号的方向改变,所以
得 x > ﹣3.
思考
这两小题中不等式的变形与方程的什么变形类似?有什么不同?
这里的变形,与方程变形中的“将未知数的系数化为 1”类似.不同的是它依据不等式的性质 2 或性质 3,通过判断不等式两边都乘以(或都除以)的数是正数还是负数,从而确定不等号的方向是否改变.
1. 设 m > n,用“>”或“<”填空.
(1)m – 5 ____ n – 5
(2)m + 4 ____ n + 4
(3)6m ____ 6n
(4)– 3m ____ – 3n
>
>
>
<
2. 设 a > b,用“>”或“<”填空.
(1)2a – 5 ____ 2b – 5;
(2)– 3.5a + 1 _____ – 3.5b + 1
>
<
3. 若 x > y ,则下列各式错误的是( )
A. x – 3 > y – 3 B. 3 – x > 3 – y
C. x + 2 > y + 2 D. x < y
B
4. 根据不等式的基本性质,把下列不等式化成 x > a 或 x < a 的形式.
(1)x – 2 < 3 (2)6x < 5x – 1
(1)解:x – 2 + 2 < 3 + 2
x < 5
(2)解:6x – 5x < 5x – 1 – 5x
x< – 1
(3) x > 5 (4) – 4x > 3
x > 5
(3)解: x×3>5×3
(4)解:– 4x×( )< 3×( )
5. 由 x < y 得 mx > my 的条件是( )
A . m ≥ 0 B . m ≤ 0 C. m > 0 D. m < 0
6.若 mx < m,且 x > 1,则应为( )
A. m < 0 B. m > 0 C. m ≤ 0 D. m ≥ 0
D
A
7. 若 m 是有理数,则 – 7m 与 3m 的大小关系应是 ( )
A. – 7m < 3m B. – 7m > 3m
C. – 7m ≤ 3m D. 不能确定
D
这节课你学了哪些内容?你有何收获或感受?
还有哪些需要老师和同学们帮你解决的问题吗?
你还有什么新的见解?
等式有哪些性质?
(1)等式的两边都加上(或减去)同一个数或同一个整式,所得的结果仍是等式.
若 a = b,则 a + c = b + c(或 a – c = b – c)
(2)等式的两边都乘以(或除以)同一个数(除数不能为零),所得的结果仍是等式.
若 a = b,则 ac = bc(或 ,c ≠ 0)
如图所示,一个倾斜的天平两边分别放有重物,其质量分别为 a 和 b(显然 a < b)
b
a
如果在两边盘内分别加上等质量的砝码 c,
b
a
c
c
那么盘子仍然像原来那样倾斜,即:
a + c < b + c
概括
不等式的性质 1 如果 a > b,那么
a + c > b + c,a – c > b – c
这就是说,不等式的两边都加上(或都减去)同一个数或同一个整式,不等号的方向不变.
思考
不等式的两边都乘以(或都除以)同一个不为零的数,不等号的方向是否也不变呢?
试一试
将不等式 7 > 4 的两边都乘以同一个数,比较所得结果的大小,用“<”、“>”或“=”号填空:
7×3 __ 4×3
7×2 __ 4×2
7÷ 5 __ 4÷5
7÷ 7 __ 4÷7
发现:不等式的两边都乘以(或除以)同一个正数,不等号的方向不变.
>
>
>
>
试一试
将不等式 7 > 4 的两边都乘以同一个数,比较所得结果的大小,用“<”、“>”或“=”号填空:
7×(– 3)__ 4×(– 3)
7×( – 2)__ 4×(– 2)
7 ÷( – 4)__ 4÷(– 4)
7 ÷( – 7)__ 4÷(– 7)
<
<
<
<
发现:不等式的两边都乘以(或除以)同一个负数,不等号的方向 改变 .
概括
不等式的性质 2 如果 a>b,并且 c>0,那么
不等式的性质 3 如果 a>b,并且 c<0,那么
这就是说,不等式的两边都乘以(或都除以)同一个正数,不等号的方向不变;不等式的两边都乘以(或都除以)同一个负数,不等号的方向改变.
例 1 解不等式:
(1)x – 7 < 8 ; (2)3x < 2x – 3.
解(1)不等式的两边都加上 7,不等号的方向不变,所以
x – 7 + 7 < 8 + 7
得 x < 15.
例 1 解不等式:
(1)x – 7 < 8 ; (2)3x < 2x – 3 .
解(2)不等式的两边都减去 2x(即都加上 – 2x),不等号的方向不变,所以
3x – 2x < 2x – 3 – 2x
得 x< – 3.
试总结一下:怎样进行不等式的“移项”?
例 2 解不等式:
(1) ; (2)﹣2x < 6.
解(1)不等式的两边都乘以 2,不等号的方向不变,所以
得 x > ﹣6.
例 2 解不等式:
(1) ; (2)– 2x < 6.
解(2)不等式的两边都除以 – 2(即都乘以 ),不等号的方向改变,所以
得 x > ﹣3.
思考
这两小题中不等式的变形与方程的什么变形类似?有什么不同?
这里的变形,与方程变形中的“将未知数的系数化为 1”类似.不同的是它依据不等式的性质 2 或性质 3,通过判断不等式两边都乘以(或都除以)的数是正数还是负数,从而确定不等号的方向是否改变.
1. 设 m > n,用“>”或“<”填空.
(1)m – 5 ____ n – 5
(2)m + 4 ____ n + 4
(3)6m ____ 6n
(4)– 3m ____ – 3n
>
>
>
<
2. 设 a > b,用“>”或“<”填空.
(1)2a – 5 ____ 2b – 5;
(2)– 3.5a + 1 _____ – 3.5b + 1
>
<
3. 若 x > y ,则下列各式错误的是( )
A. x – 3 > y – 3 B. 3 – x > 3 – y
C. x + 2 > y + 2 D. x < y
B
4. 根据不等式的基本性质,把下列不等式化成 x > a 或 x < a 的形式.
(1)x – 2 < 3 (2)6x < 5x – 1
(1)解:x – 2 + 2 < 3 + 2
x < 5
(2)解:6x – 5x < 5x – 1 – 5x
x< – 1
(3) x > 5 (4) – 4x > 3
x > 5
(3)解: x×3>5×3
(4)解:– 4x×( )< 3×( )
5. 由 x < y 得 mx > my 的条件是( )
A . m ≥ 0 B . m ≤ 0 C. m > 0 D. m < 0
6.若 mx < m,且 x > 1,则应为( )
A. m < 0 B. m > 0 C. m ≤ 0 D. m ≥ 0
D
A
7. 若 m 是有理数,则 – 7m 与 3m 的大小关系应是 ( )
A. – 7m < 3m B. – 7m > 3m
C. – 7m ≤ 3m D. 不能确定
D
这节课你学了哪些内容?你有何收获或感受?
还有哪些需要老师和同学们帮你解决的问题吗?
你还有什么新的见解?
