华东师大版数学七年级下册课件:9.1.1.认识三角形(共31张PPT)
文档属性
| 名称 | 华东师大版数学七年级下册课件:9.1.1.认识三角形(共31张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 962.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-15 00:00:00 | ||
图片预览










文档简介
1. 认识三角形
9.1 三角形
新课导入
生活中的三角形
新课探索
三角形是我们早就认识的几何图形,它是由三条不在同一条直线上的线段首尾顺次连结组成的平面图形,这三条线段就是三角形的边.
A
B
C
△ABC
三角形中内角的一边与另一边的反向延长线所组成的角叫做三角形的外角.
A
B
C
三角形的内角
三角形的外角
D
顶点
边
在三角形中,每两条边所组成的角叫做三角形的内角,
A
B
C
思考
有多少个内角?多少个外角?与内角∠A相邻的外角有几个?它们是什么关系?怎样画出△ABC 的外角?
有 3 个内角,6 个外角.
与内角∠A 相邻的外角有 2 个,它们是对顶角.
将△ABC 的一个内角的一边延长,延长线与该顶点处三角形的另一条边所夹的角就是三角形的一个外角.
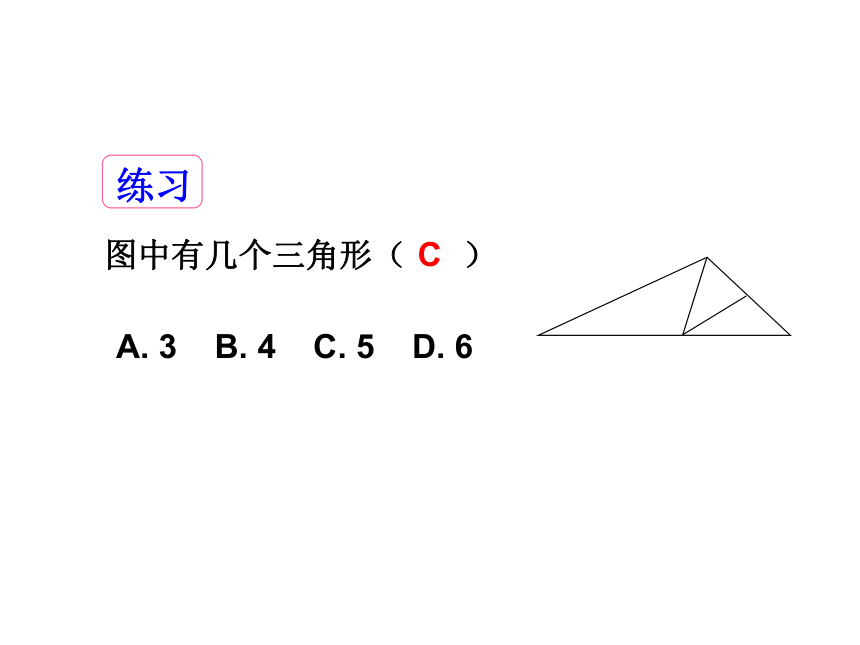
练习
图中有几个三角形( )
A. 3 B. 4 C. 5 D. 6
C
试
一
试
图中三个三角形的内角各有什么特点?
(1)
(3)
(2)
三个内角均为锐角
有一个内角是直角
有一个内角是钝角
三角形可以按角来分类:
所有内角都是锐角——锐角三角形;
有一个内角是直角——直角三角形;
有一个内角是钝角——钝角三角形.
锐角
三角形
钝角
三角形
直角
三角形
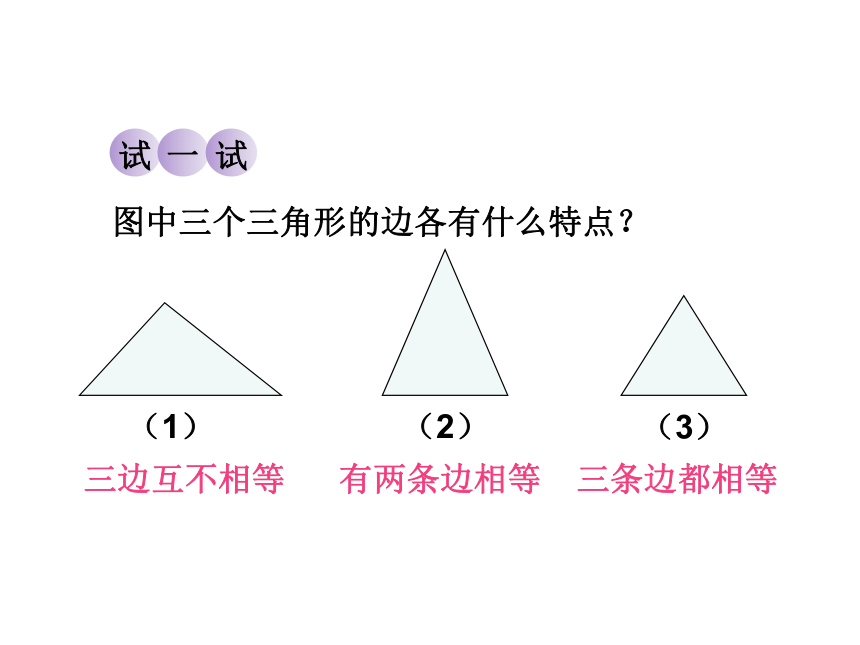
试
一
试
图中三个三角形的边各有什么特点?
(1)
(2)
(3)
三边互不相等
有两条边相等
三条边都相等
我们把有两条边相等的三角形称为等腰三角形,相等的两边叫做等腰三角形的腰;把三条边都相等的三角形称为等边三角形(或正三角形).
下列说法中错误的是( )
A. 等腰三角形可能是钝角三角形
B. 等边三角形是等腰三角形
C. 等腰三角形一定是锐角三角形
D. 等边三角形一定是锐角三角形
练习
C
取△ABC 边 AB 的中点 E ,连结 CE,线段 CE 就是△ABC 的一条中线.
A
B
C
E
做
一
做
画出锐角三角形的三条中线,你发现了什么?
锐角三角形的三条中线交于一点.
画出三个三角形的中线,你有什么结论?
三角形的三条中线交于一点.
如图,AD,BE,CF 是△ABC 的三条中线.
(1)AC = AE = EC;
CD = ;
AF = AB;
(2)若 S△ABC = 12 cm2,
则 S△ABD = .
A
B
C
D
E
F
G
练习
2
2
BD
6 cm?
作△ABC 的内角∠BAC 的平分线交对边 BC 于点 D,线段 AD 就是△ABC 的一条角平分线.
A
B
C
D
1
2
做
一
做
画出锐角三角形的三条角平分线,你发现了什么?
锐角三角形的三条角平分线交于一点.
画出三个三角形的角平分线,你有什么结论?
三角形的三条角平分线交于一点.
练习
如图,AD 是△ABC 的中线,AE 是∠BAC 的平分线,则 BD = ________ = BC,∠BAE = _________ = ∠BAC.
DC
∠CAE
过顶点 B 作△ABC 的边 AC 的垂线,垂足为点 F,线段 BF 就是△ABC 的一条高.
A
B
C
F
做
一
做
画出锐角三角形的三条高,你发现了什么?
锐角三角形的三条高交于一点.
画出三个三角形的高,你有什么结论?
三角形的三条高(或所在的直线)交于一点.
解:△ABE,△ABD,△ABC,△AED,△AEC,△ADC.
如图,写出以 AE 为高的三角形.
练习
课堂小结
认识三角形
锐角
三角形
钝角
三角形
直角
三角形
1. 在下图中,正确画出△ABC 中边 BC 上高的是( )
随堂演练
C
A
D
C
B
A
D
C
B
A
D
C
B
A
D
C
B
A.
B.
C.
D.
S△ABC = 2S△ABM = 40 平方厘米
2. 如图所示,AM 是△ABC 的中线,△ABM的面积是 20 平方厘米,求△ABC 的面积.
3. 如图,AD,BE,CF 是△ABC 的三条角平分线,则:
∠1 = ;
∠3 = ;
∠ACB = 2 .
∠2
∠ABC 或∠ABE
∠4 或∠ACF
A
B
C
D
E
F
1
2
3
4
4. 以下说法错误的是( )
A. 三角形的三条高一定在三角形内部交于一点
B. 三角形的三条中线一定在三角形内部交于一点
C. 三角形的三条角平分线一定在三角形内部交于一点
D. 一个三角形的三条高、中线、角平分线分别交于同一个点
A
5. 如图,AD 是△ABC 的边 BC 上的中线,已知 AB = 5 cm,AC = 3 cm.△ABD 的面积为 a cm2,
(1)S△ABC = ______cm2;
(2)△ABD 与△ACD 的周长之差为___cm.
2a
2
6. 在 △ABC 中,AD 是 ∠A 的平分线,DE∥AC 交 AB 于 E,EF∥AD 交 BC 于 F,试问 EF 是△BED 的角平分线吗?说说你的理由.
解:EF 是 △BED 的角平分线,理由如下:
∵AD 是∠BAC 的平分线,∴∠1 =∠2.
∵ DE∥AC,
∴∠5 =∠2 =∠1.
∵EF∥AD,
∴∠3 =∠5,∠4 =∠1,
∴∠3 =∠4,
∴EF 是△BED 的角平分线.
9.1 三角形
新课导入
生活中的三角形
新课探索
三角形是我们早就认识的几何图形,它是由三条不在同一条直线上的线段首尾顺次连结组成的平面图形,这三条线段就是三角形的边.
A
B
C
△ABC
三角形中内角的一边与另一边的反向延长线所组成的角叫做三角形的外角.
A
B
C
三角形的内角
三角形的外角
D
顶点
边
在三角形中,每两条边所组成的角叫做三角形的内角,
A
B
C
思考
有多少个内角?多少个外角?与内角∠A相邻的外角有几个?它们是什么关系?怎样画出△ABC 的外角?
有 3 个内角,6 个外角.
与内角∠A 相邻的外角有 2 个,它们是对顶角.
将△ABC 的一个内角的一边延长,延长线与该顶点处三角形的另一条边所夹的角就是三角形的一个外角.
练习
图中有几个三角形( )
A. 3 B. 4 C. 5 D. 6
C
试
一
试
图中三个三角形的内角各有什么特点?
(1)
(3)
(2)
三个内角均为锐角
有一个内角是直角
有一个内角是钝角
三角形可以按角来分类:
所有内角都是锐角——锐角三角形;
有一个内角是直角——直角三角形;
有一个内角是钝角——钝角三角形.
锐角
三角形
钝角
三角形
直角
三角形
试
一
试
图中三个三角形的边各有什么特点?
(1)
(2)
(3)
三边互不相等
有两条边相等
三条边都相等
我们把有两条边相等的三角形称为等腰三角形,相等的两边叫做等腰三角形的腰;把三条边都相等的三角形称为等边三角形(或正三角形).
下列说法中错误的是( )
A. 等腰三角形可能是钝角三角形
B. 等边三角形是等腰三角形
C. 等腰三角形一定是锐角三角形
D. 等边三角形一定是锐角三角形
练习
C
取△ABC 边 AB 的中点 E ,连结 CE,线段 CE 就是△ABC 的一条中线.
A
B
C
E
做
一
做
画出锐角三角形的三条中线,你发现了什么?
锐角三角形的三条中线交于一点.
画出三个三角形的中线,你有什么结论?
三角形的三条中线交于一点.
如图,AD,BE,CF 是△ABC 的三条中线.
(1)AC = AE = EC;
CD = ;
AF = AB;
(2)若 S△ABC = 12 cm2,
则 S△ABD = .
A
B
C
D
E
F
G
练习
2
2
BD
6 cm?
作△ABC 的内角∠BAC 的平分线交对边 BC 于点 D,线段 AD 就是△ABC 的一条角平分线.
A
B
C
D
1
2
做
一
做
画出锐角三角形的三条角平分线,你发现了什么?
锐角三角形的三条角平分线交于一点.
画出三个三角形的角平分线,你有什么结论?
三角形的三条角平分线交于一点.
练习
如图,AD 是△ABC 的中线,AE 是∠BAC 的平分线,则 BD = ________ = BC,∠BAE = _________ = ∠BAC.
DC
∠CAE
过顶点 B 作△ABC 的边 AC 的垂线,垂足为点 F,线段 BF 就是△ABC 的一条高.
A
B
C
F
做
一
做
画出锐角三角形的三条高,你发现了什么?
锐角三角形的三条高交于一点.
画出三个三角形的高,你有什么结论?
三角形的三条高(或所在的直线)交于一点.
解:△ABE,△ABD,△ABC,△AED,△AEC,△ADC.
如图,写出以 AE 为高的三角形.
练习
课堂小结
认识三角形
锐角
三角形
钝角
三角形
直角
三角形
1. 在下图中,正确画出△ABC 中边 BC 上高的是( )
随堂演练
C
A
D
C
B
A
D
C
B
A
D
C
B
A
D
C
B
A.
B.
C.
D.
S△ABC = 2S△ABM = 40 平方厘米
2. 如图所示,AM 是△ABC 的中线,△ABM的面积是 20 平方厘米,求△ABC 的面积.
3. 如图,AD,BE,CF 是△ABC 的三条角平分线,则:
∠1 = ;
∠3 = ;
∠ACB = 2 .
∠2
∠ABC 或∠ABE
∠4 或∠ACF
A
B
C
D
E
F
1
2
3
4
4. 以下说法错误的是( )
A. 三角形的三条高一定在三角形内部交于一点
B. 三角形的三条中线一定在三角形内部交于一点
C. 三角形的三条角平分线一定在三角形内部交于一点
D. 一个三角形的三条高、中线、角平分线分别交于同一个点
A
5. 如图,AD 是△ABC 的边 BC 上的中线,已知 AB = 5 cm,AC = 3 cm.△ABD 的面积为 a cm2,
(1)S△ABC = ______cm2;
(2)△ABD 与△ACD 的周长之差为___cm.
2a
2
6. 在 △ABC 中,AD 是 ∠A 的平分线,DE∥AC 交 AB 于 E,EF∥AD 交 BC 于 F,试问 EF 是△BED 的角平分线吗?说说你的理由.
解:EF 是 △BED 的角平分线,理由如下:
∵AD 是∠BAC 的平分线,∴∠1 =∠2.
∵ DE∥AC,
∴∠5 =∠2 =∠1.
∵EF∥AD,
∴∠3 =∠5,∠4 =∠1,
∴∠3 =∠4,
∴EF 是△BED 的角平分线.
