华东师大版数学七年级下册课件:9.1.2.三角形的内角和与外角和(共30张PPT)
文档属性
| 名称 | 华东师大版数学七年级下册课件:9.1.2.三角形的内角和与外角和(共30张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 747.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-15 12:26:26 | ||
图片预览






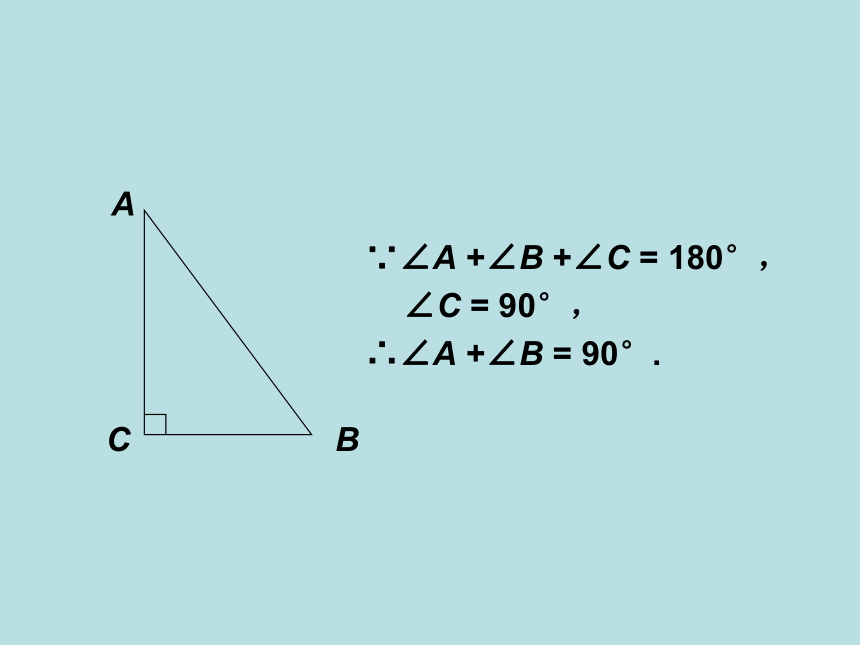
文档简介
2. 三角形的内角和与外角和
新课导入
在小学我们曾剪下三角形的两个内角,将它们写第三个内角拼在起,发现三个内角恰好拼成了一个平角.
3
1
1
2
2
2
1
3
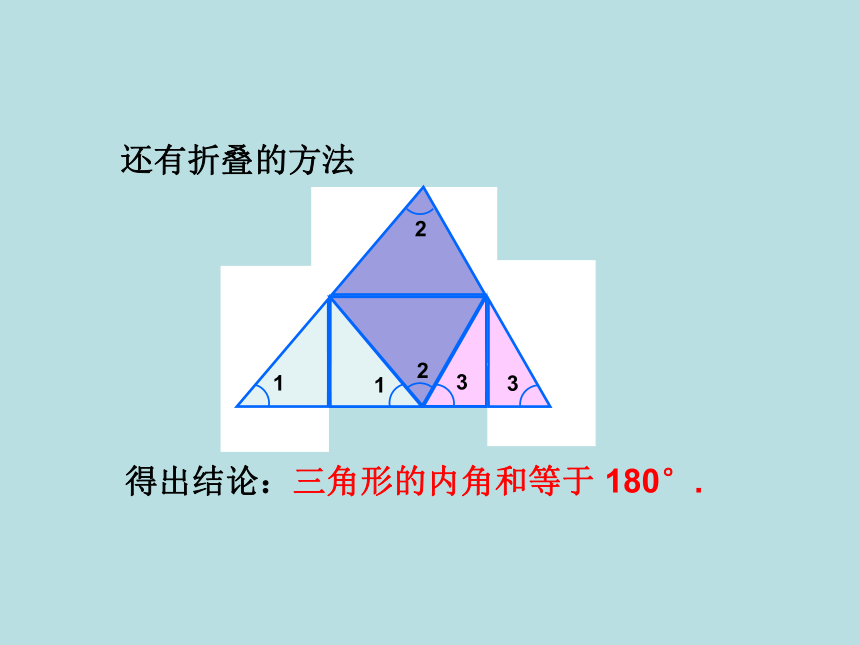
还有折叠的方法
得出结论:三角形的内角和等于 180°.
新课探索
如图,已知△ABC,分别用∠1、∠2、∠3 表示△ABC 的三个内角,证明∠1 +∠2 +∠3 = 180°.
A
B
C
1
2
3
你还有其他方法吗?
A
B
C
1
2
3
解 延长 BC 至点 E,以点 C为顶点,在 BE 的上侧作∠DCE =∠2,
E
D
∵CD // BA,
∴∠1 =∠ACD(两直线平行,内错角相等).
∵∠3 +∠ACD +∠DCE = 180°,
∴∠1 +∠2 +∠3 = 180°.
则 CD// BA(同位角相等两直线平行).
A
B
C
1
2
3
∵ ∠1 + ∠4 + ∠5 = 180°(平角定义),
∴ ∠A + ∠B + ∠C = 180°(等量代换).
证明:过点 A 作直线 l ,使 l ∥BC.
∵ l ∥BC ,
∴ ∠2 = ∠4,
∠3 = ∠5
(两直线平行,内错角相等).
4
5
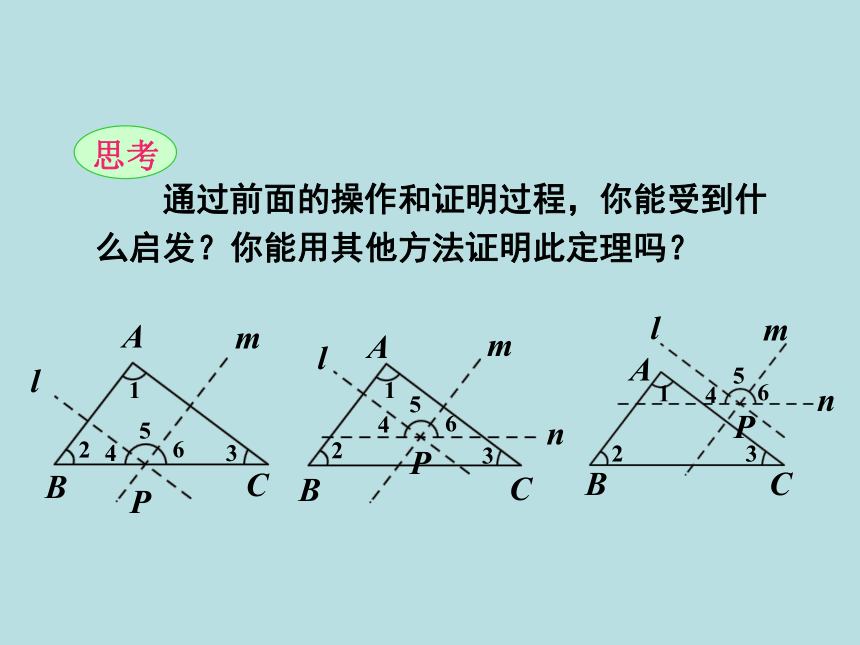
思考
通过前面的操作和证明过程,你能受到什么启发?你能用其他方法证明此定理吗?
C
A
B
1
2
3
4
5
l
P
6
m
C
A
B
1
2
3
4
5
l
P
6
m
n
C
A
B
1
2
3
4
5
l
P
6
m
n
A
C
B
由三角形的内角和等于180°,容易得出下面的结论:
直角三角形的两个锐角互余.
你能说明其理由吗?
A
C
B
∵∠A +∠B +∠C = 180°,
∠C = 90°,
∴∠A +∠B = 90°.
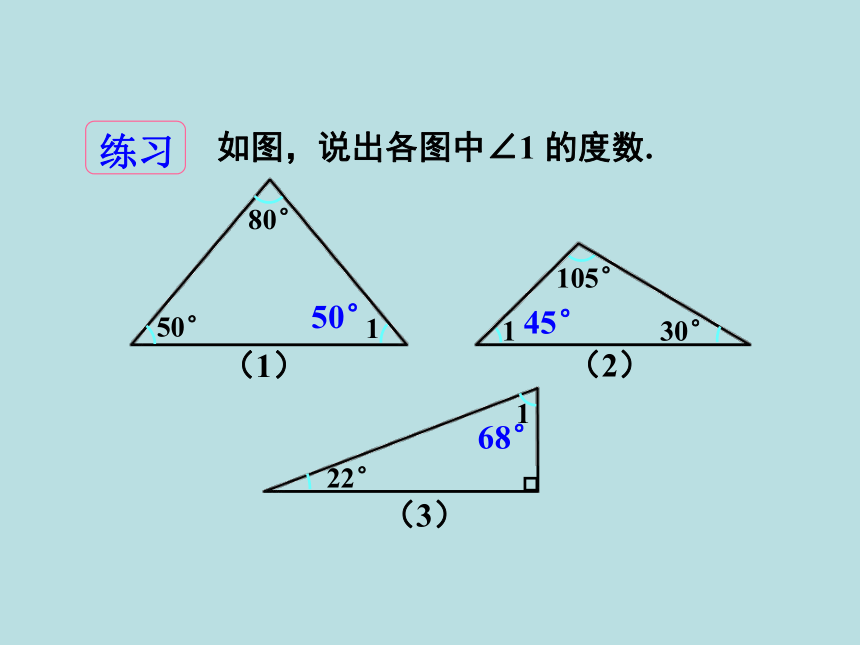
练习
如图,说出各图中∠1 的度数.
30°
105°
1
(2)
80°
50°
1
(1)
22°
1
(3)
50°
45°
68°
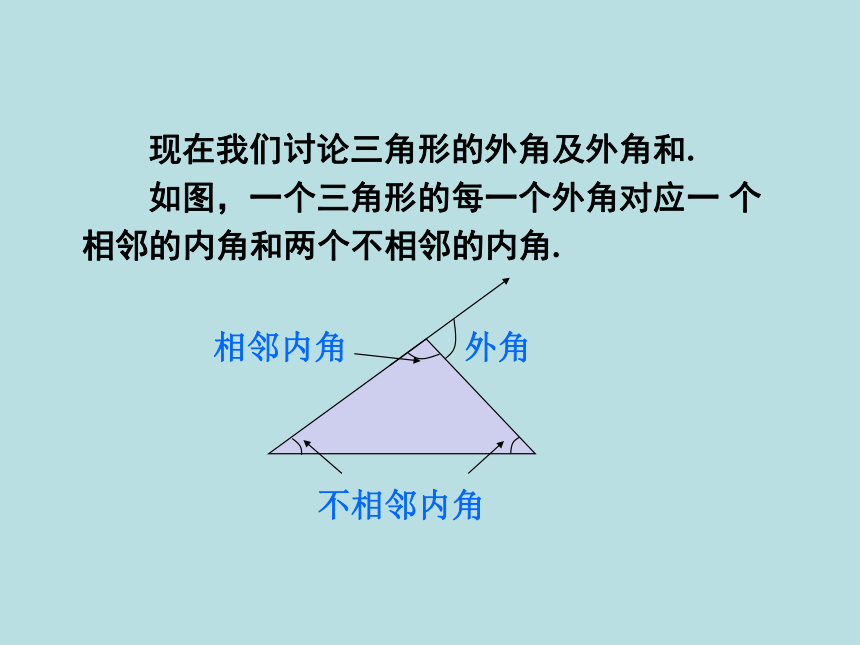
现在我们讨论三角形的外角及外角和.
如图,一个三角形的每一个外角对应一 个相邻的内角和两个不相邻的内角.
外角
相邻内角
不相邻内角
A
B
C
D
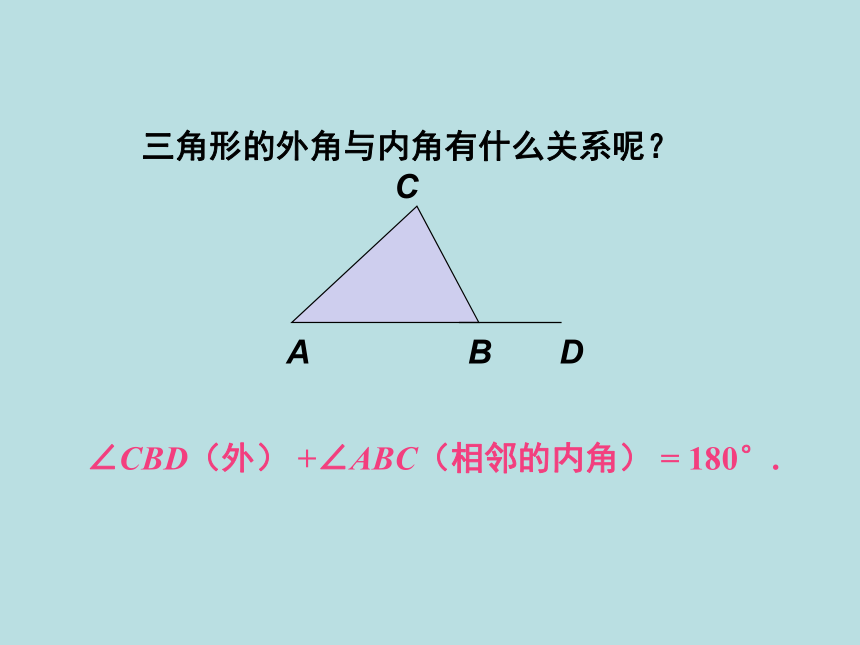
三角形的外角与内角有什么关系呢?
∠CBD(外) +∠ABC(相邻的内角) = 180°.
A
B
C
D
那么外角∠CBD 与其他两个不相邻的内角又有什么关系呢?
依据三角形的内角和等于 180°,我们有
∠ACB +∠BAC +∠ABC = 180°.
由上面两个式子,可以推出
∠CBD = 180°– ∠ABC,
∠ACB +∠BAC =180°– ∠ABC.
A
B
C
D
那么外角∠CBD 与其他两个不相邻的内角又有什么关系呢?
A
B
C
D
那么外角∠CBD 与其他两个不相邻的内角又有什么关系呢?
因而可以得到结论:
∠CBD =∠ACB +∠BAC.
由此可知,三角形的外角有两条性质:
1. 三角形的一个外角等于与它不相邻的两个内角的和.
2. 三角形的一个外角大于任何一个与它不相邻的内角.
练习
∠C
∠3
∠DAC
∠4
如图,口答:
(1)∠1 = + ;
(2)∠2 = + .
B
A
C
D
1
2
3
4
A
B
C
1
2
3
∠1 +∠2 +∠3 是△ABC 的外角和.
∠1 +_______ = 180°,
∠2 +_______ = 180°,
∠3 +_______ = 180°.
∠ACB
∠BAC
∠ABC
三式相加可以得到
∠ 1 +∠2 +∠3 +______+______+______=______,
∠ACB
∠BAC
∠ABC
540°
而 ∠ACB +∠BAC + ∠ABC = 180°,
可以得到
∠1 +∠2 +∠3 = 360°.
三角形的外角和等于360°.
你能证明吗?
A
B
C
1
2
3
D
证明:过点 A 作 AD∥BC,
∴∠1 = ∠EAD,
∠3 = ∠BAD.
又∵∠2 +∠BAD +∠EAD = 360°,
∴ ∠1 +∠2 +∠3 = 360°.
E
例 1 如图,D 是△ABC 的边 BC 上一点,∠B =∠BAD,∠ADC = 80°,∠BAC = 70°.
求:(1)∠B 的度数;
(2)∠C 的度数.
A
B
D
C
A
B
D
C
解??(1)∵∠ADC 是△ABD 的外角(已知),
∴∠B +∠BAD =?∠ADC?=?80°(三角形的一?个外角等于与它不相邻的两个内角的和).
又∵∠B =∠BAD(已知),
∠B?=?80°× = 40°(等量代换).
1
2
A
B
D
C
(2)∵∠B +∠BAC +∠C = 180°(三角形的内角和等于180°),
∴∠C = 180°– ∠B – ∠BAC(等式的性质)
= 180° – 40° – 70°
= 70°.
练习
(1) (2) (3)
1
1
1
2
2
2
60°
80°
30°
40°
40°
∠1 = 40°
∠2 = 140°
∠1 = 110°
∠2 = 70°
∠1 = 50°
∠2 = 140°
如图,说出图形中∠1 和∠2 的度数:
课堂小结
三角形的内角和等于 180°.
直角三角形的两个锐角互余.
三角形的外角和等于360°.
随堂演练
1.△ABC 中,∠A : ∠B : ∠C = 1 : 2 : 3,则∠A =______,∠B = ______,∠C = ______.
90°
30°
60°
2. 如图,∠1 = _______.
3. 如图,AB∥CD,∠A = 40°,∠D = 45°,则∠1 = _______.
110°
85°
第2题图 第3题图
4. 如图,说出图形中∠1 的度数.
图中∠1的度数依次为:90°,85°, 95°,45°.
(1) (2)
(3) (4)
30°
60°
1
35°
60°
1
45°
50°
1
30°
15°
1
5. 如图,从 A 处观测 C 处的仰角∠CAD = 30°,从 B 处观测 C 处的仰角∠CBD = 45°. 从 C 处观测 A,B 两处的视角∠ACB 是多少?
A
B
D
C
∠ACB =∠CBD – ∠CAD
= 45°– 30°= 15°.
6. 如图,是一个五角星,求∠A+∠B+∠C+∠D+∠E的度数.
解:∵∠AFG =∠B +∠D,
∠AGF =∠C +∠E,
∠A +∠AFG +∠AGF =180°,
∴∠A +∠B +∠C +∠D +∠E = 180°.
F
G
新课导入
在小学我们曾剪下三角形的两个内角,将它们写第三个内角拼在起,发现三个内角恰好拼成了一个平角.
3
1
1
2
2
2
1
3
还有折叠的方法
得出结论:三角形的内角和等于 180°.
新课探索
如图,已知△ABC,分别用∠1、∠2、∠3 表示△ABC 的三个内角,证明∠1 +∠2 +∠3 = 180°.
A
B
C
1
2
3
你还有其他方法吗?
A
B
C
1
2
3
解 延长 BC 至点 E,以点 C为顶点,在 BE 的上侧作∠DCE =∠2,
E
D
∵CD // BA,
∴∠1 =∠ACD(两直线平行,内错角相等).
∵∠3 +∠ACD +∠DCE = 180°,
∴∠1 +∠2 +∠3 = 180°.
则 CD// BA(同位角相等两直线平行).
A
B
C
1
2
3
∵ ∠1 + ∠4 + ∠5 = 180°(平角定义),
∴ ∠A + ∠B + ∠C = 180°(等量代换).
证明:过点 A 作直线 l ,使 l ∥BC.
∵ l ∥BC ,
∴ ∠2 = ∠4,
∠3 = ∠5
(两直线平行,内错角相等).
4
5
思考
通过前面的操作和证明过程,你能受到什么启发?你能用其他方法证明此定理吗?
C
A
B
1
2
3
4
5
l
P
6
m
C
A
B
1
2
3
4
5
l
P
6
m
n
C
A
B
1
2
3
4
5
l
P
6
m
n
A
C
B
由三角形的内角和等于180°,容易得出下面的结论:
直角三角形的两个锐角互余.
你能说明其理由吗?
A
C
B
∵∠A +∠B +∠C = 180°,
∠C = 90°,
∴∠A +∠B = 90°.
练习
如图,说出各图中∠1 的度数.
30°
105°
1
(2)
80°
50°
1
(1)
22°
1
(3)
50°
45°
68°
现在我们讨论三角形的外角及外角和.
如图,一个三角形的每一个外角对应一 个相邻的内角和两个不相邻的内角.
外角
相邻内角
不相邻内角
A
B
C
D
三角形的外角与内角有什么关系呢?
∠CBD(外) +∠ABC(相邻的内角) = 180°.
A
B
C
D
那么外角∠CBD 与其他两个不相邻的内角又有什么关系呢?
依据三角形的内角和等于 180°,我们有
∠ACB +∠BAC +∠ABC = 180°.
由上面两个式子,可以推出
∠CBD = 180°– ∠ABC,
∠ACB +∠BAC =180°– ∠ABC.
A
B
C
D
那么外角∠CBD 与其他两个不相邻的内角又有什么关系呢?
A
B
C
D
那么外角∠CBD 与其他两个不相邻的内角又有什么关系呢?
因而可以得到结论:
∠CBD =∠ACB +∠BAC.
由此可知,三角形的外角有两条性质:
1. 三角形的一个外角等于与它不相邻的两个内角的和.
2. 三角形的一个外角大于任何一个与它不相邻的内角.
练习
∠C
∠3
∠DAC
∠4
如图,口答:
(1)∠1 = + ;
(2)∠2 = + .
B
A
C
D
1
2
3
4
A
B
C
1
2
3
∠1 +∠2 +∠3 是△ABC 的外角和.
∠1 +_______ = 180°,
∠2 +_______ = 180°,
∠3 +_______ = 180°.
∠ACB
∠BAC
∠ABC
三式相加可以得到
∠ 1 +∠2 +∠3 +______+______+______=______,
∠ACB
∠BAC
∠ABC
540°
而 ∠ACB +∠BAC + ∠ABC = 180°,
可以得到
∠1 +∠2 +∠3 = 360°.
三角形的外角和等于360°.
你能证明吗?
A
B
C
1
2
3
D
证明:过点 A 作 AD∥BC,
∴∠1 = ∠EAD,
∠3 = ∠BAD.
又∵∠2 +∠BAD +∠EAD = 360°,
∴ ∠1 +∠2 +∠3 = 360°.
E
例 1 如图,D 是△ABC 的边 BC 上一点,∠B =∠BAD,∠ADC = 80°,∠BAC = 70°.
求:(1)∠B 的度数;
(2)∠C 的度数.
A
B
D
C
A
B
D
C
解??(1)∵∠ADC 是△ABD 的外角(已知),
∴∠B +∠BAD =?∠ADC?=?80°(三角形的一?个外角等于与它不相邻的两个内角的和).
又∵∠B =∠BAD(已知),
∠B?=?80°× = 40°(等量代换).
1
2
A
B
D
C
(2)∵∠B +∠BAC +∠C = 180°(三角形的内角和等于180°),
∴∠C = 180°– ∠B – ∠BAC(等式的性质)
= 180° – 40° – 70°
= 70°.
练习
(1) (2) (3)
1
1
1
2
2
2
60°
80°
30°
40°
40°
∠1 = 40°
∠2 = 140°
∠1 = 110°
∠2 = 70°
∠1 = 50°
∠2 = 140°
如图,说出图形中∠1 和∠2 的度数:
课堂小结
三角形的内角和等于 180°.
直角三角形的两个锐角互余.
三角形的外角和等于360°.
随堂演练
1.△ABC 中,∠A : ∠B : ∠C = 1 : 2 : 3,则∠A =______,∠B = ______,∠C = ______.
90°
30°
60°
2. 如图,∠1 = _______.
3. 如图,AB∥CD,∠A = 40°,∠D = 45°,则∠1 = _______.
110°
85°
第2题图 第3题图
4. 如图,说出图形中∠1 的度数.
图中∠1的度数依次为:90°,85°, 95°,45°.
(1) (2)
(3) (4)
30°
60°
1
35°
60°
1
45°
50°
1
30°
15°
1
5. 如图,从 A 处观测 C 处的仰角∠CAD = 30°,从 B 处观测 C 处的仰角∠CBD = 45°. 从 C 处观测 A,B 两处的视角∠ACB 是多少?
A
B
D
C
∠ACB =∠CBD – ∠CAD
= 45°– 30°= 15°.
6. 如图,是一个五角星,求∠A+∠B+∠C+∠D+∠E的度数.
解:∵∠AFG =∠B +∠D,
∠AGF =∠C +∠E,
∠A +∠AFG +∠AGF =180°,
∴∠A +∠B +∠C +∠D +∠E = 180°.
F
G
