华东师大版数学七年级下册课件:9.3.1.用相同的正多边形(共22张PPT)
文档属性
| 名称 | 华东师大版数学七年级下册课件:9.3.1.用相同的正多边形(共22张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 938.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-15 12:28:04 | ||
图片预览







文档简介
9.3 用正多边形铺设地面
1. 用相同的正多边形
新课导入
图片欣赏
新课探索
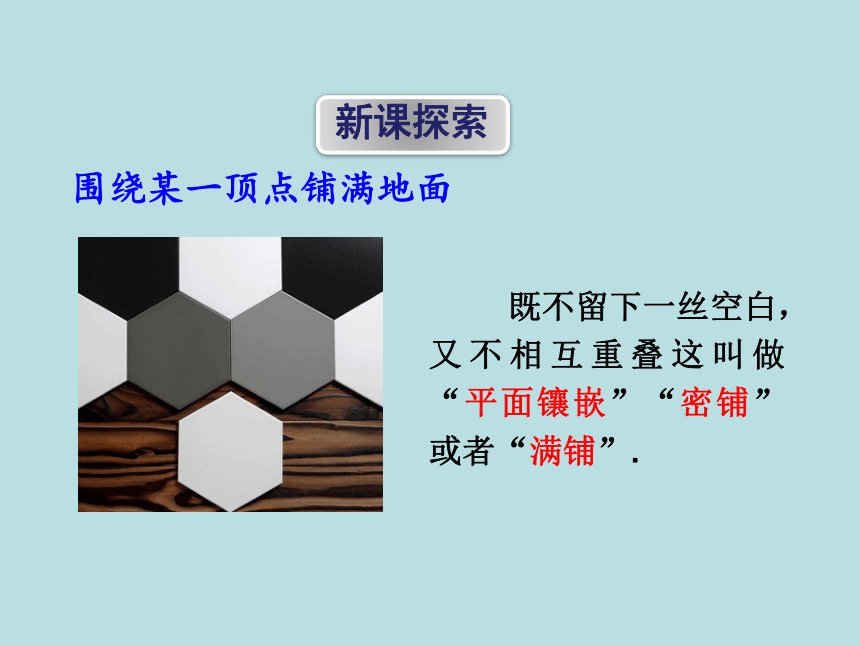
围绕某一顶点铺满地面
既不留下一丝空白,又不相互重叠这叫做“平面镶嵌”“密铺”或者“满铺”.
用同一种正多边形铺地板,哪些能密铺不留空隙呢?
探索
这显然与正多边形的内角大小有关.
回答下列问题:
1. 什么叫正多边形?
2. n 边形的内角和是什么?正 n 边形的内角怎么表示?外角和是什么?
什么是正多边形?
如果多边形的各边都相等,各内角也都相等,那么就称它为正多边形.
① n 边形的内角和公式:
(n – 2) ×180°
② n 边形的外角和:
360°
③正 n 边形每个内角 =
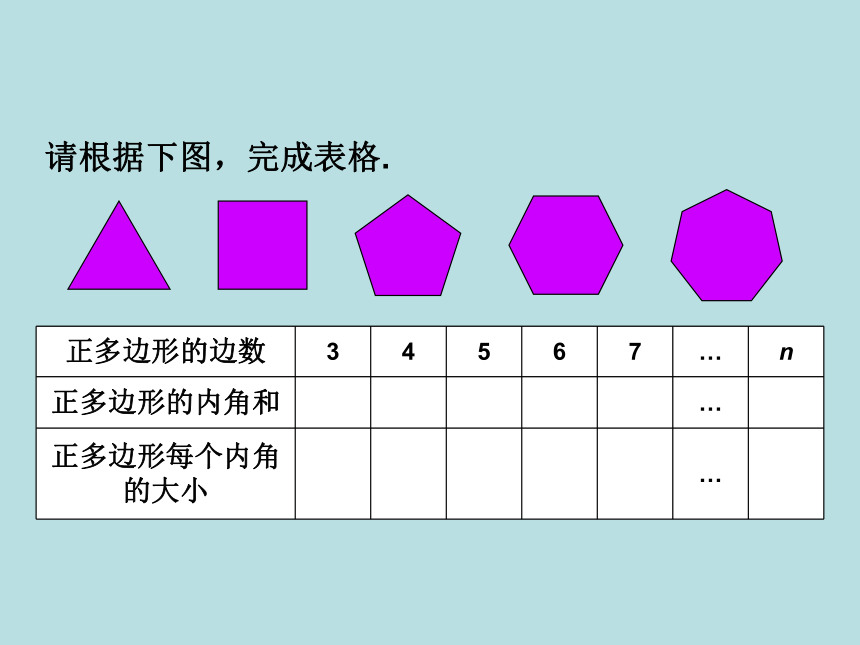
请根据下图,完成表格.
正多边形的边数
3
4
5
6
7
…
n
正多边形的内角和
…
正多边形每个内角的大小
…
60°×6 = 360°
正三角形瓷砖
60°
60°
60°
60°
60°
60°
正四边形瓷砖
90°
90°
90°
90°
90°×4 = 360°
正五边形瓷砖
108°
108°
108°
108°×3 = 324°
正六边形瓷砖
120°
120°
120°
120°×3 = 360°
正八边形瓷砖
135°
135°
135°
135°×3 = 405°
现在,你知道镶嵌的规律了吗?
概括
使用给定的某种正多边形,当围绕一点拼在一起的几个内角和加在一起恰好组成一个周角(360°)时,就能拼成一个平面图形.
想
一
想
正七边形、正九边形、正十边形、正十二边形能密铺地面吗?为什么?
能用同一种正多边形拼地板的正多边形有正三角形、正方形、正六边形.
小结:
课堂小结
通过这节课的学习活动,你有什么收获?
随堂演练
1. 用一种正多边形能进行平面铺设的条件是( )
A. 内角都是整数度数
B. 边数是 3 的整数倍
C. 内角整除 180°
D. 内角整除 360°
D
2. 下列正多边形的地砖中,不能铺满地面的正多边形是( )
A. 正三角形 B. 正方形
C. 正五边形 D. 正六边形
3. 用同一种正六边形拼成一个平面时,在每一个顶点处有_______个正六边形.
C
3
4. 铺设一间长 6 m、宽 3.5 m 的客厅地面需要同样规格的正方形地板砖,现有“40 cm×40 cm”“30 cm×30 cm”“50 cm×50 cm”和“60 cm×60 cm”的地板砖,请你设计一下,要想全部铺满,不锯破且不留一点空隙,选哪一种规格?为什么?需要多少块?
解:选“50 cm×50 cm”规格的.
理由:∵6 m =600c m,3.5 m = 350 cm,
600,350 都是 50 的倍数,
∴选“50 cm×5 0cm”规格的.
需要 7×12 = 84(块).
1. 用相同的正多边形
新课导入
图片欣赏
新课探索
围绕某一顶点铺满地面
既不留下一丝空白,又不相互重叠这叫做“平面镶嵌”“密铺”或者“满铺”.
用同一种正多边形铺地板,哪些能密铺不留空隙呢?
探索
这显然与正多边形的内角大小有关.
回答下列问题:
1. 什么叫正多边形?
2. n 边形的内角和是什么?正 n 边形的内角怎么表示?外角和是什么?
什么是正多边形?
如果多边形的各边都相等,各内角也都相等,那么就称它为正多边形.
① n 边形的内角和公式:
(n – 2) ×180°
② n 边形的外角和:
360°
③正 n 边形每个内角 =
请根据下图,完成表格.
正多边形的边数
3
4
5
6
7
…
n
正多边形的内角和
…
正多边形每个内角的大小
…
60°×6 = 360°
正三角形瓷砖
60°
60°
60°
60°
60°
60°
正四边形瓷砖
90°
90°
90°
90°
90°×4 = 360°
正五边形瓷砖
108°
108°
108°
108°×3 = 324°
正六边形瓷砖
120°
120°
120°
120°×3 = 360°
正八边形瓷砖
135°
135°
135°
135°×3 = 405°
现在,你知道镶嵌的规律了吗?
概括
使用给定的某种正多边形,当围绕一点拼在一起的几个内角和加在一起恰好组成一个周角(360°)时,就能拼成一个平面图形.
想
一
想
正七边形、正九边形、正十边形、正十二边形能密铺地面吗?为什么?
能用同一种正多边形拼地板的正多边形有正三角形、正方形、正六边形.
小结:
课堂小结
通过这节课的学习活动,你有什么收获?
随堂演练
1. 用一种正多边形能进行平面铺设的条件是( )
A. 内角都是整数度数
B. 边数是 3 的整数倍
C. 内角整除 180°
D. 内角整除 360°
D
2. 下列正多边形的地砖中,不能铺满地面的正多边形是( )
A. 正三角形 B. 正方形
C. 正五边形 D. 正六边形
3. 用同一种正六边形拼成一个平面时,在每一个顶点处有_______个正六边形.
C
3
4. 铺设一间长 6 m、宽 3.5 m 的客厅地面需要同样规格的正方形地板砖,现有“40 cm×40 cm”“30 cm×30 cm”“50 cm×50 cm”和“60 cm×60 cm”的地板砖,请你设计一下,要想全部铺满,不锯破且不留一点空隙,选哪一种规格?为什么?需要多少块?
解:选“50 cm×50 cm”规格的.
理由:∵6 m =600c m,3.5 m = 350 cm,
600,350 都是 50 的倍数,
∴选“50 cm×5 0cm”规格的.
需要 7×12 = 84(块).
