华东师大版数学七年级下册课件:9.3.2.用多种正多边形(共23张PPT)
文档属性
| 名称 | 华东师大版数学七年级下册课件:9.3.2.用多种正多边形(共23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-15 12:28:18 | ||
图片预览




文档简介
2. 用多种正多边形
新课导入
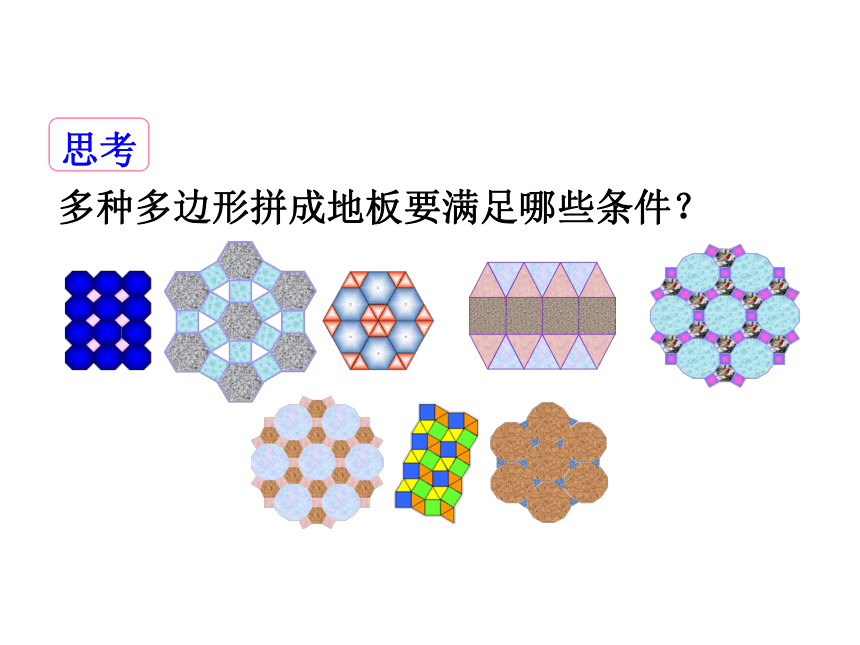
思考
用同一种平面图形如果不能铺满地板,用两种或者两种以上平面图形能不能铺满地板呢?
新课探索
多种正多边形拼地板问题.
探索
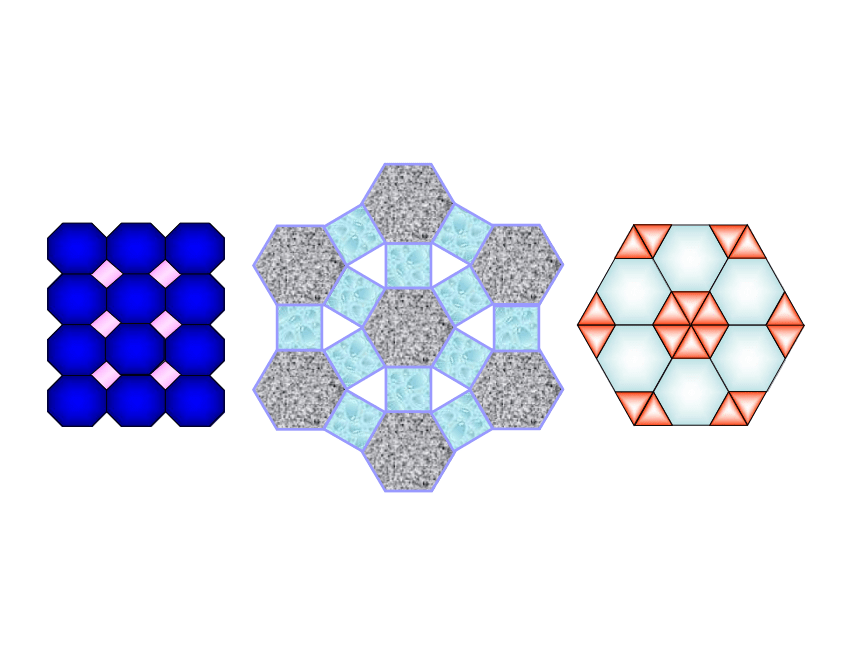
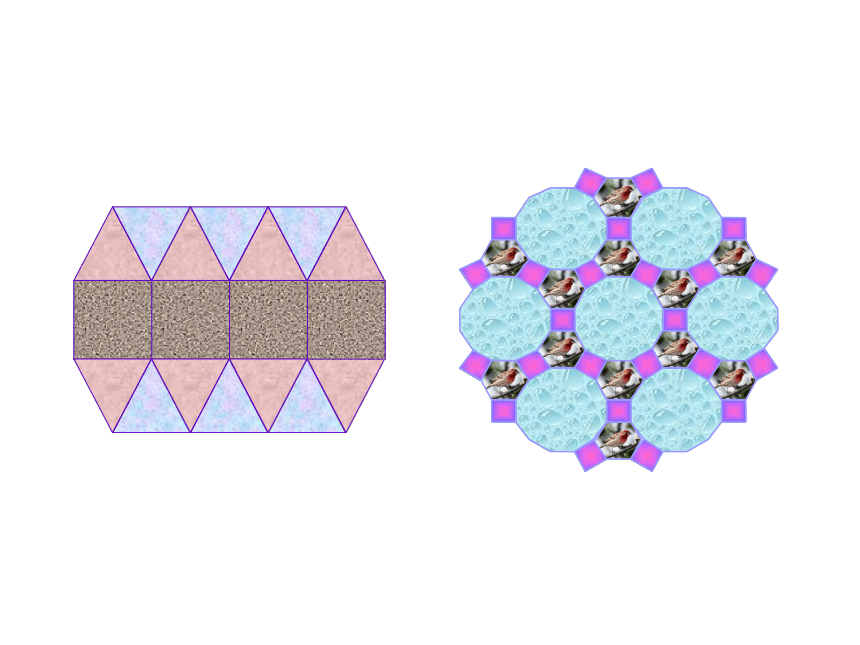
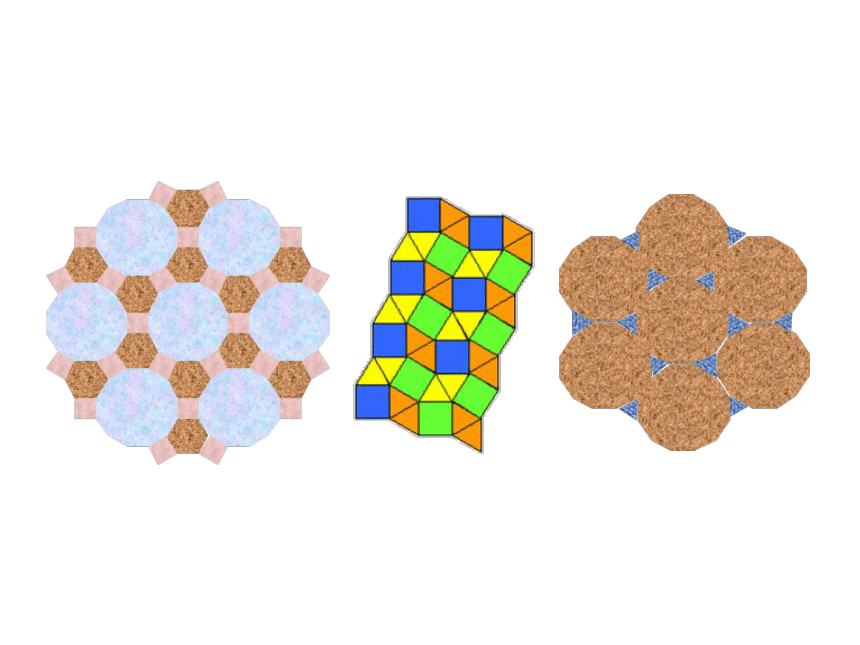
实际上,美观的图案是需要多种图形的,下面请同学们看一看哪几种正多边形可拼成地板?拼成什么样的图案?
多种多边形拼成地板要满足哪些条件?
思考
概括
围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角时,就拼成一个平面图形,就说它们能拼地板.
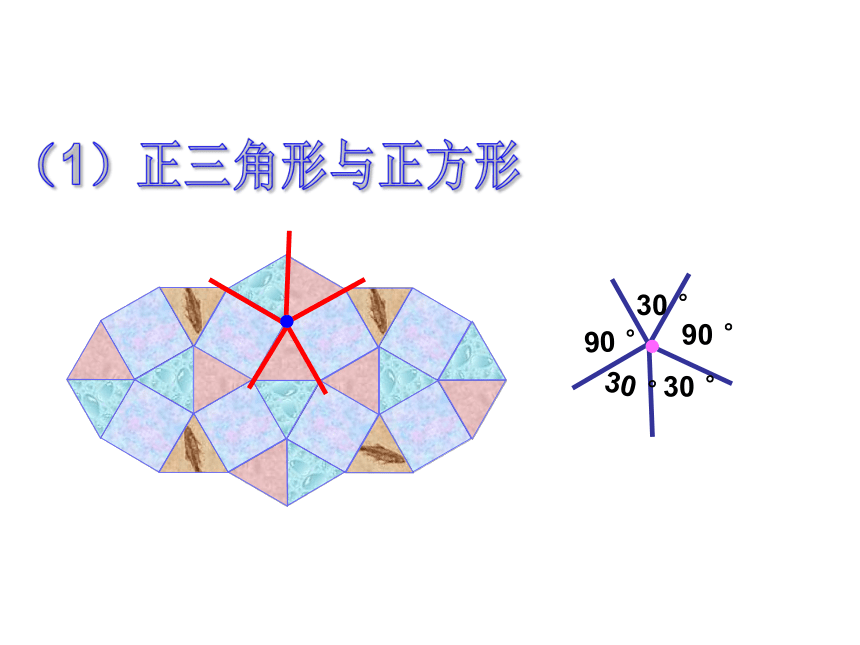
90 °
90 °
30 °
30 °
30 °
30 °
90 °
90 °
30 °
30 °
120°
120°
60°
60°
60°
60°
120°
60°
60°
135 °
90 °
135 °
思考:还有其它的组合吗?
正十二边形与正方形、正六边形的平面密铺.
正六边形与正方形、正三角形的平面密铺.
练习
1. 下列两种正多边形的组合能否密铺地面?
正三角形与正方形?
正三角形与正五边形?
正三角形与正六边形?
正四边形与正六边形?
正三角形与正十二边形?
2. 用正五边形和什么多边形能铺满地板?
课堂小结
通过这节课的学习活动,你有什么收获?
随堂演练
1. 下列不能铺满地面的正多边形组合是( )
A. 正三角形和正方形
B. 正三角形和正六边形
C. 正方形和正八边形
D. 正五边形和正八边形
D
2. 设在一个顶点周围有 a 个正三角形,b 个正十二边形铺满地面,则 a =______, b=______.
1
2
3. 现有四种地板砖,它们的形状别是正三角形、正方形、正六边形、正八边形,且它们的边长都相等. 同时选择其中两种地板砖密铺地面,选择的方式有( )
A. 2 种 B. 3 种 C. 4 种 D. 5 种
B
4. 如图,正多边形 A,B,C 密铺地面,其中 A 为正六边形,C 为正方形,请通过计算求出正多边形 B 的边数.
解:设正多边形B的边数为 n,
∵一个点处由 1 个正六边形、1 个正方形、1 个多边形 B 组成,则正多边形B的一个内角的度数为
360°– 120°– 90°= 150°,
则(n – 2)·180°= n·150°,
解得 n = 12.
∴正多边形 B 的边数为12.
新课导入
思考
用同一种平面图形如果不能铺满地板,用两种或者两种以上平面图形能不能铺满地板呢?
新课探索
多种正多边形拼地板问题.
探索
实际上,美观的图案是需要多种图形的,下面请同学们看一看哪几种正多边形可拼成地板?拼成什么样的图案?
多种多边形拼成地板要满足哪些条件?
思考
概括
围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角时,就拼成一个平面图形,就说它们能拼地板.
90 °
90 °
30 °
30 °
30 °
30 °
90 °
90 °
30 °
30 °
120°
120°
60°
60°
60°
60°
120°
60°
60°
135 °
90 °
135 °
思考:还有其它的组合吗?
正十二边形与正方形、正六边形的平面密铺.
正六边形与正方形、正三角形的平面密铺.
练习
1. 下列两种正多边形的组合能否密铺地面?
正三角形与正方形?
正三角形与正五边形?
正三角形与正六边形?
正四边形与正六边形?
正三角形与正十二边形?
2. 用正五边形和什么多边形能铺满地板?
课堂小结
通过这节课的学习活动,你有什么收获?
随堂演练
1. 下列不能铺满地面的正多边形组合是( )
A. 正三角形和正方形
B. 正三角形和正六边形
C. 正方形和正八边形
D. 正五边形和正八边形
D
2. 设在一个顶点周围有 a 个正三角形,b 个正十二边形铺满地面,则 a =______, b=______.
1
2
3. 现有四种地板砖,它们的形状别是正三角形、正方形、正六边形、正八边形,且它们的边长都相等. 同时选择其中两种地板砖密铺地面,选择的方式有( )
A. 2 种 B. 3 种 C. 4 种 D. 5 种
B
4. 如图,正多边形 A,B,C 密铺地面,其中 A 为正六边形,C 为正方形,请通过计算求出正多边形 B 的边数.
解:设正多边形B的边数为 n,
∵一个点处由 1 个正六边形、1 个正方形、1 个多边形 B 组成,则正多边形B的一个内角的度数为
360°– 120°– 90°= 150°,
则(n – 2)·180°= n·150°,
解得 n = 12.
∴正多边形 B 的边数为12.
