华东师大版数学七年级下册课件:第9章 多边形 单元复习(共24张PPT)
文档属性
| 名称 | 华东师大版数学七年级下册课件:第9章 多边形 单元复习(共24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 610.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-15 12:43:28 | ||
图片预览



文档简介
第9章 多边形
复习
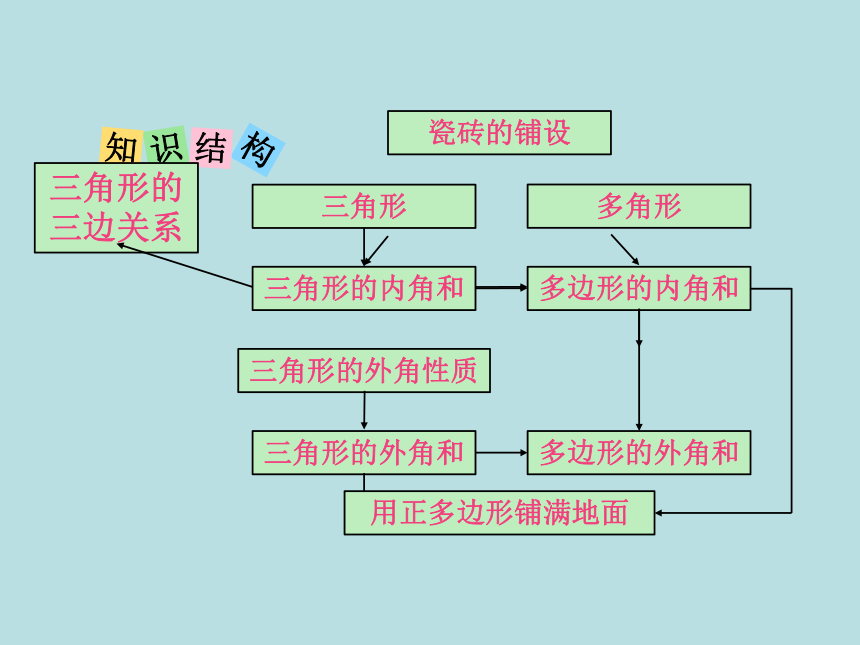
识
构
结
知
三角形
三角形的内角和
三角形的外角性质
三角形的外角和
三角形的三边关系
瓷砖的铺设
多角形
多边形的内角和
多边形的外角和
用正多边形铺满地面
识
点
要
知
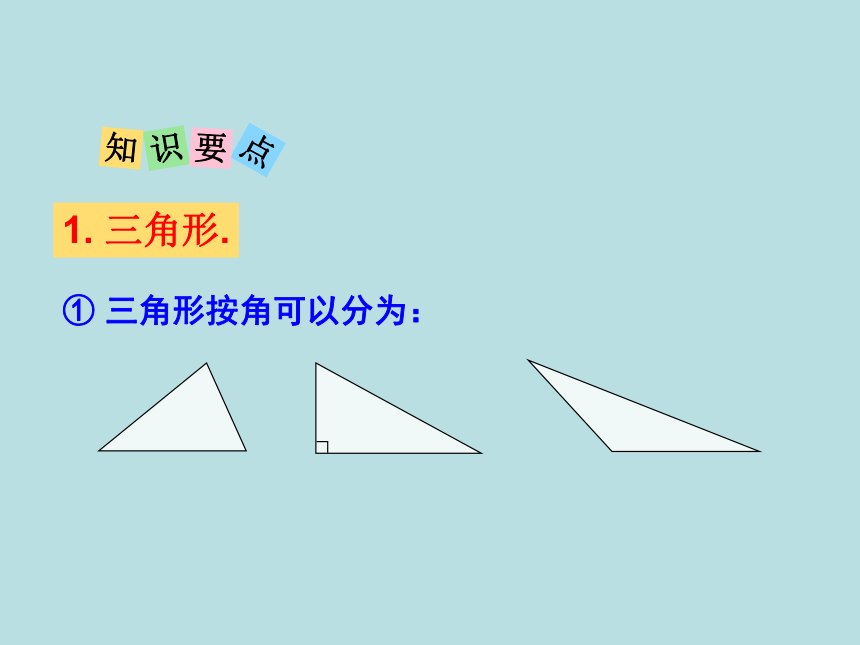
1. 三角形.
① 三角形按角可以分为:
② 我们把两条边相等的三角形称为等腰三角形,相等的两边叫做等腰三角形的腰;把三条边都相等的三角形叫做等边三角形(或正三角形).
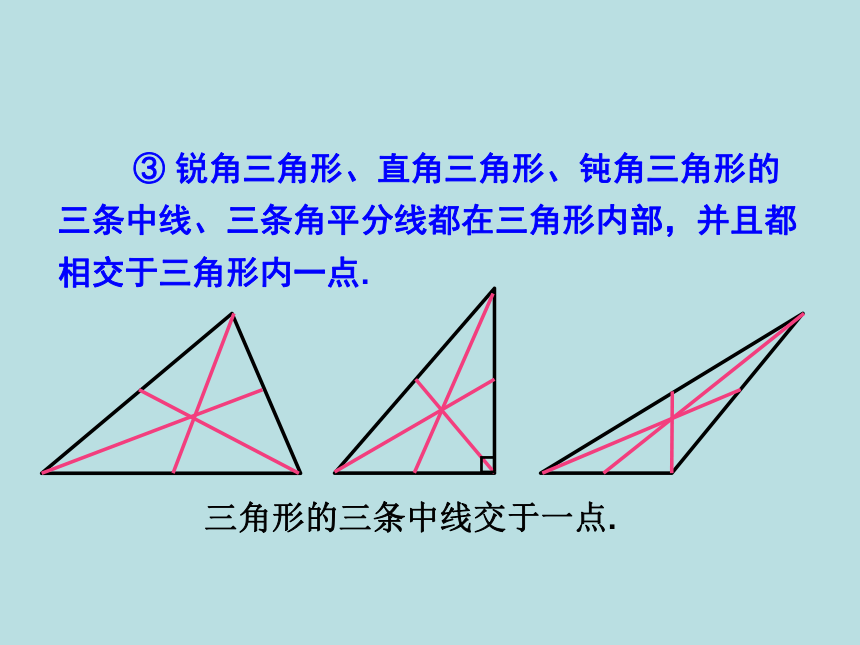
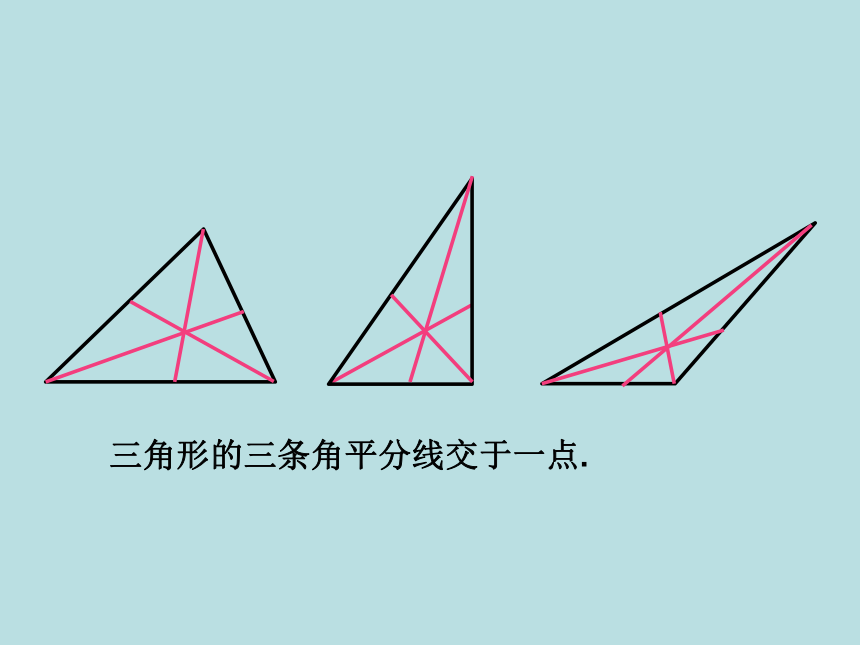
③ 锐角三角形、直角三角形、钝角三角形的三条中线、三条角平分线都在三角形内部,并且都相交于三角形内一点.
三角形的三条中线交于一点.
三角形的三条角平分线交于一点.
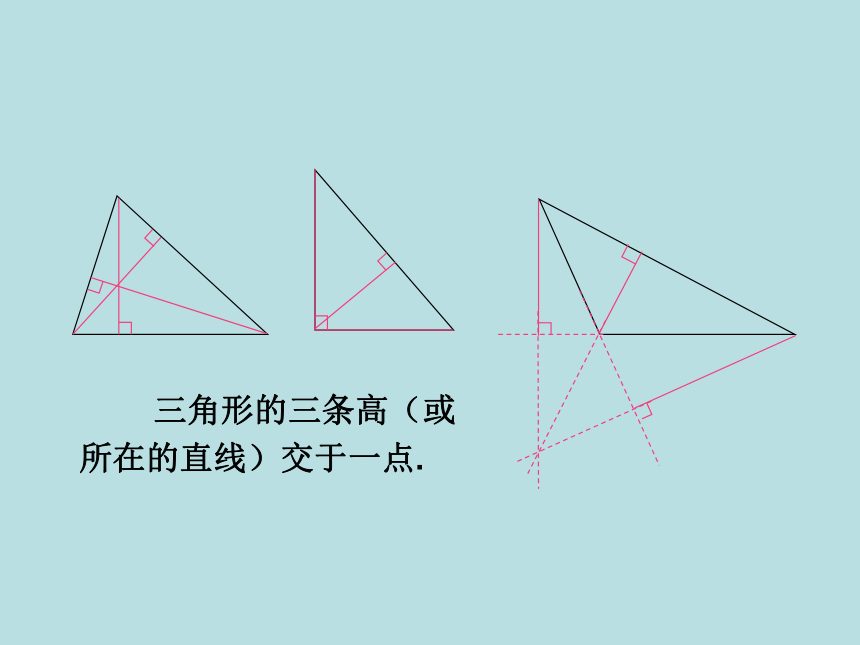
④ 锐角三角形的三条高相交于三角形内一点,直角三角形的三条高相交于直角顶点,钝角三角形的两条高位于三角形的外部且三条高所在的直线交于三角形外一点.
三角形的三条高(或所在的直线)交于一点.
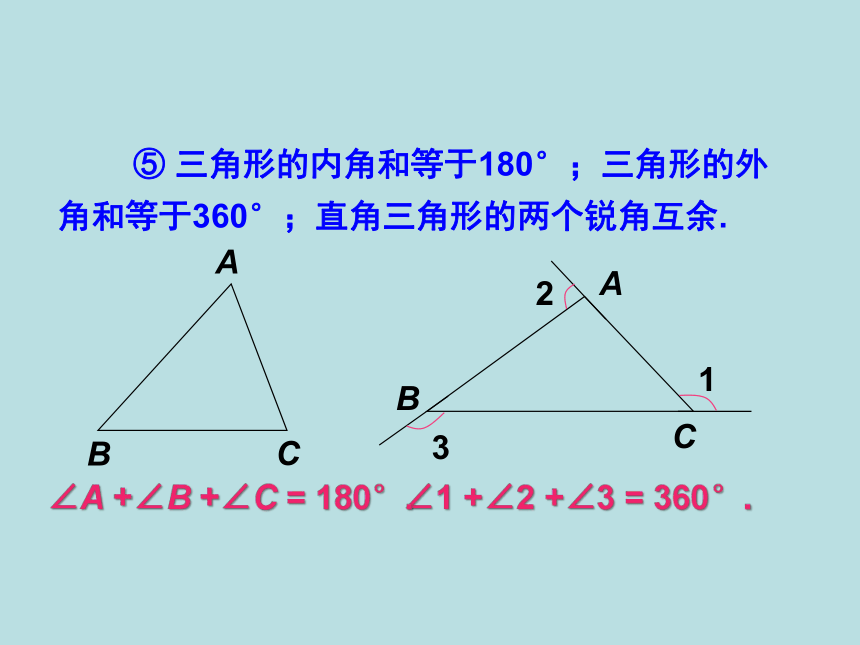
⑤ 三角形的内角和等于180°;三角形的外角和等于360°;直角三角形的两个锐角互余.
A
B
C
1
2
3
∠1 +∠2 +∠3 = 360°.
A
B
C
∠A +∠B +∠C = 180°.
⑥ 三角形的外角性质:
(1)三角形的一个外角等于和它不相邻的两个内角的和;
(2)三角形的一个外角大于任何一个与它不相邻的内角.
⑦ 三角形的任意两边的和大于第三边.
a
b
c
a + b > c
a + c > b
b + c > a
⑧ 三角形稳定性,四边形具有不稳定性.
2. 多边形.
① 正多边形:如果多边形的各边都相等,各内角也都相等,那么就称它为正多边形.
正三角形
正方形
正五边形
② 连结多边形不相邻的两个顶点的线段叫做多边形的对角线.
③ n 边形的内角和为(n – 2)·180°;
n 边形一共有 条对角线;
任意多边形的外角和都为 360°.
3. 用正多边形铺设地面.
① 当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角时,就拼成一个平面图形;
② 若几个正多边形的内角的和等于 360°,那么这几个正多边形可铺满地面.
随堂演练
1. 已知三角形的三边长分别是 3,8,x,若 x 的值为偶数,则 x 的值有( )
A. 6 个 B. 5 个 C. 4 个 D. 3 个
D
2. 下列关于三角形按边分类的集合中,正确的是( )
D
3. 三角形周长为 10,其中有两边相等且长为整数,则第三边长为_________.
4 或 2
4. 已知:如图,AB∥CD,∠B = 45°,∠BED = 78°,求∠D 的度数.
解:如图,延长 BE 交 CD 于点 F,
∵AB∥CD,∠B = 45°,
∴∠1 =∠B = 45°,
∴∠D =∠BED – ∠1 = 78°– 45°= 33°
A
B
C
D
E
F
1
5. 在△ABC 中,∠ABC =∠C,BD 是 AC 边上的高,∠ABD = 30°,则∠C 的度数是多少?
分析: 要按△ABC 为锐角三角形和钝角三角形两种情况,分类讨论.
解:分两种情况讨论:
(1)当△ABC 为锐角三角形时,如图所示,在△ABD 中,
∵ BD 是 AC 边上的高,
∴ ∠ADB = 90°.
又∵∠ABD = 30°,
∴∠A = 180°– ∠ADB – ∠ABD
=180°– 90°– 30°= 60°.
又∵∠A +∠ABC +∠C = 180° ,
∴∠ABC +∠C = 120°,
又∵∠ABC =∠C,∴∠C = 60°.
(2)当△ABC 为钝角三角形时,如图所示. 在直角△ABD 中,
∵ ∠ABD = 30°,
所以∠BAD = 60°. ∴ ∠BAC = 120°.
又∵ ∠BAC +∠ABC +∠C =180°
∴ ∠ABC +∠C = 60°.
∴ ∠C = 30°.
综上所知,∠C 的度数为 60°或 30°.
6. 如下图:你能求五边形内角和吗?
五边形内角和为:
4×180°– 180°= 540°
五边形内角和为:
5 ×180°– 360° = 540°
7. 一个多边形有 14 条对角线,则它是_____边形
A. 六边形 B. 七边形 C. 十边形 D. 十一边形
B
8. 如图,求∠A +∠B +∠C +∠D +∠E +∠F 的度数.
1
2
解:连接 BE,
∵∠C +∠D +∠COD =∠1 +∠2 +∠BOE
∴ ∠C +∠D = ∠1 +∠2
∴∠A +∠ABC +∠C +∠D +∠DEF +∠F
=∠A +∠ABC +∠1 +∠2 +∠DEF +∠F
=∠A +∠ABE +∠BEF +∠F
= 360°
复习
识
构
结
知
三角形
三角形的内角和
三角形的外角性质
三角形的外角和
三角形的三边关系
瓷砖的铺设
多角形
多边形的内角和
多边形的外角和
用正多边形铺满地面
识
点
要
知
1. 三角形.
① 三角形按角可以分为:
② 我们把两条边相等的三角形称为等腰三角形,相等的两边叫做等腰三角形的腰;把三条边都相等的三角形叫做等边三角形(或正三角形).
③ 锐角三角形、直角三角形、钝角三角形的三条中线、三条角平分线都在三角形内部,并且都相交于三角形内一点.
三角形的三条中线交于一点.
三角形的三条角平分线交于一点.
④ 锐角三角形的三条高相交于三角形内一点,直角三角形的三条高相交于直角顶点,钝角三角形的两条高位于三角形的外部且三条高所在的直线交于三角形外一点.
三角形的三条高(或所在的直线)交于一点.
⑤ 三角形的内角和等于180°;三角形的外角和等于360°;直角三角形的两个锐角互余.
A
B
C
1
2
3
∠1 +∠2 +∠3 = 360°.
A
B
C
∠A +∠B +∠C = 180°.
⑥ 三角形的外角性质:
(1)三角形的一个外角等于和它不相邻的两个内角的和;
(2)三角形的一个外角大于任何一个与它不相邻的内角.
⑦ 三角形的任意两边的和大于第三边.
a
b
c
a + b > c
a + c > b
b + c > a
⑧ 三角形稳定性,四边形具有不稳定性.
2. 多边形.
① 正多边形:如果多边形的各边都相等,各内角也都相等,那么就称它为正多边形.
正三角形
正方形
正五边形
② 连结多边形不相邻的两个顶点的线段叫做多边形的对角线.
③ n 边形的内角和为(n – 2)·180°;
n 边形一共有 条对角线;
任意多边形的外角和都为 360°.
3. 用正多边形铺设地面.
① 当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角时,就拼成一个平面图形;
② 若几个正多边形的内角的和等于 360°,那么这几个正多边形可铺满地面.
随堂演练
1. 已知三角形的三边长分别是 3,8,x,若 x 的值为偶数,则 x 的值有( )
A. 6 个 B. 5 个 C. 4 个 D. 3 个
D
2. 下列关于三角形按边分类的集合中,正确的是( )
D
3. 三角形周长为 10,其中有两边相等且长为整数,则第三边长为_________.
4 或 2
4. 已知:如图,AB∥CD,∠B = 45°,∠BED = 78°,求∠D 的度数.
解:如图,延长 BE 交 CD 于点 F,
∵AB∥CD,∠B = 45°,
∴∠1 =∠B = 45°,
∴∠D =∠BED – ∠1 = 78°– 45°= 33°
A
B
C
D
E
F
1
5. 在△ABC 中,∠ABC =∠C,BD 是 AC 边上的高,∠ABD = 30°,则∠C 的度数是多少?
分析: 要按△ABC 为锐角三角形和钝角三角形两种情况,分类讨论.
解:分两种情况讨论:
(1)当△ABC 为锐角三角形时,如图所示,在△ABD 中,
∵ BD 是 AC 边上的高,
∴ ∠ADB = 90°.
又∵∠ABD = 30°,
∴∠A = 180°– ∠ADB – ∠ABD
=180°– 90°– 30°= 60°.
又∵∠A +∠ABC +∠C = 180° ,
∴∠ABC +∠C = 120°,
又∵∠ABC =∠C,∴∠C = 60°.
(2)当△ABC 为钝角三角形时,如图所示. 在直角△ABD 中,
∵ ∠ABD = 30°,
所以∠BAD = 60°. ∴ ∠BAC = 120°.
又∵ ∠BAC +∠ABC +∠C =180°
∴ ∠ABC +∠C = 60°.
∴ ∠C = 30°.
综上所知,∠C 的度数为 60°或 30°.
6. 如下图:你能求五边形内角和吗?
五边形内角和为:
4×180°– 180°= 540°
五边形内角和为:
5 ×180°– 360° = 540°
7. 一个多边形有 14 条对角线,则它是_____边形
A. 六边形 B. 七边形 C. 十边形 D. 十一边形
B
8. 如图,求∠A +∠B +∠C +∠D +∠E +∠F 的度数.
1
2
解:连接 BE,
∵∠C +∠D +∠COD =∠1 +∠2 +∠BOE
∴ ∠C +∠D = ∠1 +∠2
∴∠A +∠ABC +∠C +∠D +∠DEF +∠F
=∠A +∠ABC +∠1 +∠2 +∠DEF +∠F
=∠A +∠ABE +∠BEF +∠F
= 360°
