华师大版数学八年级下册17.3.2第1课时 一次函数的图像及平移规律 课件(共23张PPT)
文档属性
| 名称 | 华师大版数学八年级下册17.3.2第1课时 一次函数的图像及平移规律 课件(共23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-15 12:42:48 | ||
图片预览



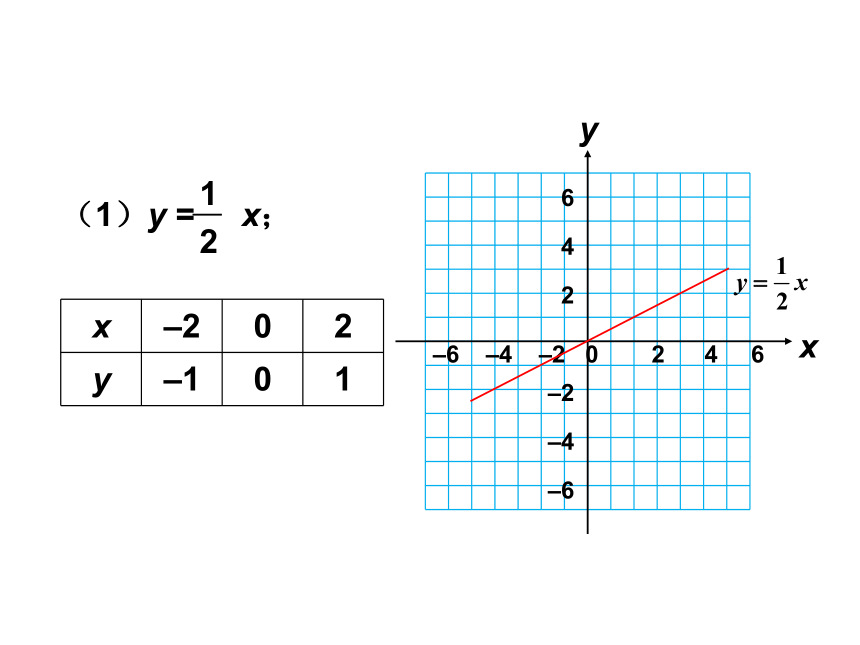
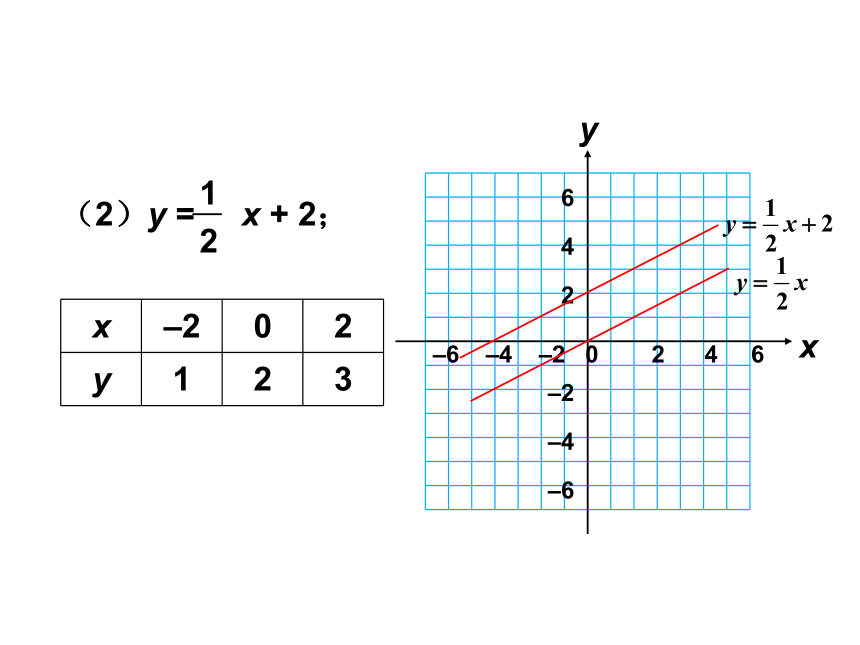
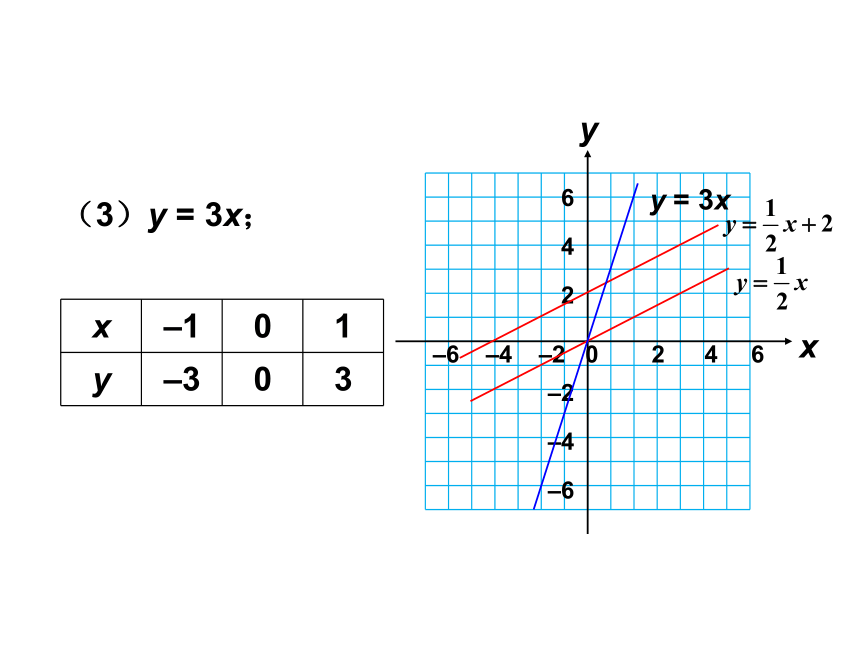
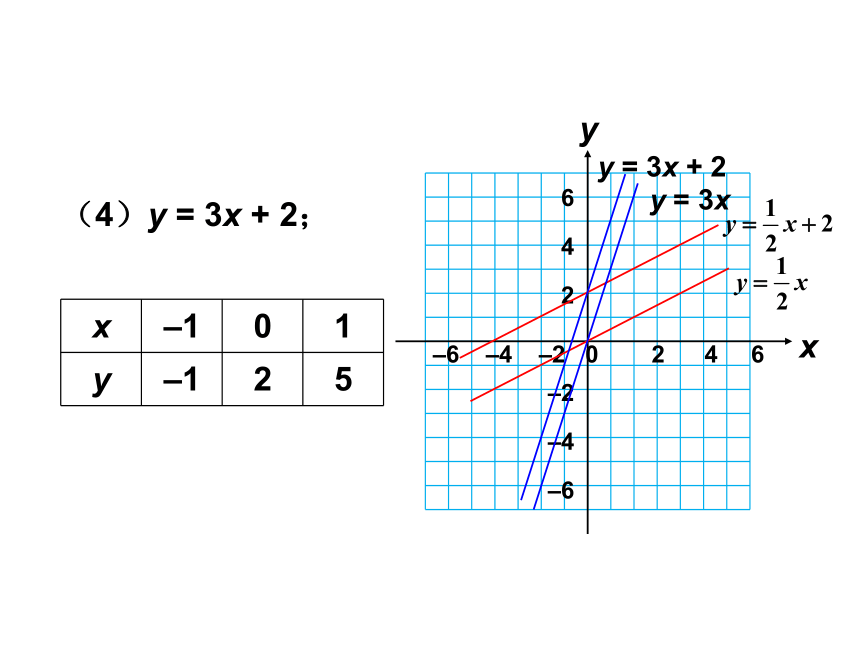

文档简介
第1课时 一次函数的图象及平移规律
华东师大版八年级数学下册
2 一次函数的图象
新课导入
我们已经学习了用描点法画函数的图象,也知道通常可以结合图象研究函数的性质和应用. 那么,一次函数的图象是什么形状呢?
新课探索
做
一
做
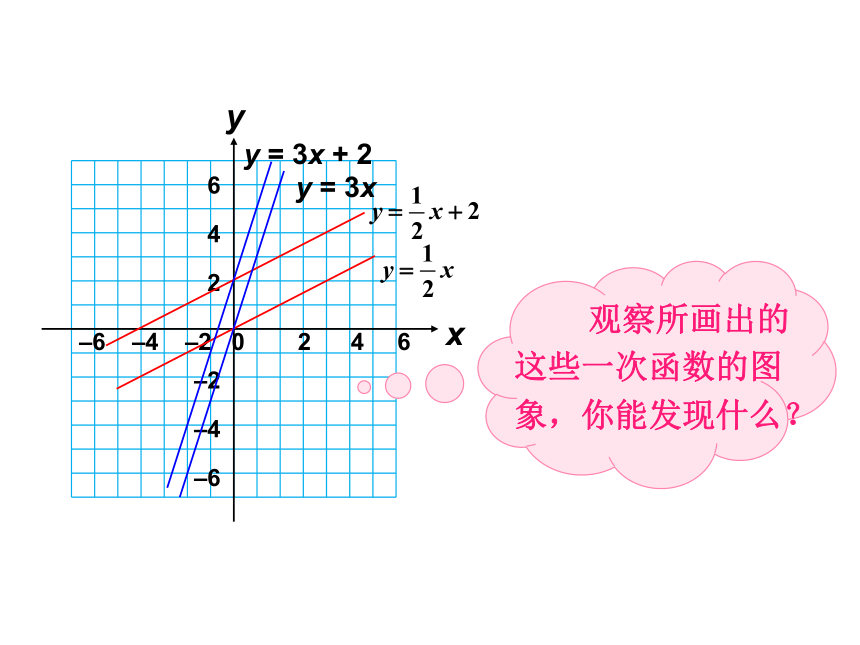
在同一平面坐标系中画出下列函数的图象:
(1)y = x;
1
2
(2)y = x + 2;
1
2
(3)y = 3x;
(4)y = 3x + 2;
(1)y = x;
1
2
x
–2
0
2
y
–1
0
1
x
y
–6 –4 –2 0 2 4 6
6
4
2
–2
–4
–6
(2)y = x + 2;
1
2
x
–2
0
2
y
1
2
3
x
y
–6 –4 –2 0 2 4 6
6
4
2
–2
–4
–6
x
y
–6 –4 –2 0 2 4 6
6
4
2
–2
–4
–6
(3)y = 3x;
x
–1
0
1
y
–3
0
3
y = 3x
x
y
–6 –4 –2 0 2 4 6
6
4
2
–2
–4
–6
(4)y = 3x + 2;
x
–1
0
1
y
–1
2
5
y = 3x
y = 3x + 2
x
y
–6 –4 –2 0 2 4 6
6
4
2
–2
–4
–6
y = 3x
y = 3x + 2
观察所画出的这些一次函数的图象,你能发现什么?
一次函数 y = kx + b (k ≠ 0)的图象是一条直线. 通常也称为直线 y = kx + b. 特别地,正比例函数 y = kx(k ≠ 0) 的图象是经过原点(0,0)的一条直线.
两点确定一条直线,画一次函数时,只需要取两个点.
讨论
观察“做一做”中画出的四个一次函数的图象,比较下列各对一次函数的图象有什么共同点,有什么不同点:
(1)y = 3x 与 y = 3x + 2;
(2)y = x 与 y = x + 2;
1
2
1
2
(3)y = 3x + 2 与 y = x + 2;
1
2
x
y
–6 –4 –2 0 2 4 6
6
4
2
–2
–4
–6
y = 3x
y = 3x + 2
两个一次函数,当系
数 k 相同,b 不相同时(如
y = 3x 与 y = 3x + 2 )有:
共同点:___________
不同点:_______________
两直线平行
与 y 轴交点不同
x
y
–6 –4 –2 0 2 4 6
6
4
2
–2
–4
–6
y = 3x
y = 3x + 2
由图看出 y = 3x + 2 可以由 y = 3x 沿 y 轴向上平移 2 个单位得到.
y = x + 2 可以由 y = x 沿 y 轴向上平移 2 个单位得到.
1
2
1
2
由正比例函数 y = kx + b 的图象向上平移 h(h > 0)个单位,可得一次函数 y = kx +(b + h)的图象;
由正比例函数 y = kx + b 的图象向下平移 h(h > 0)个单位,可得一次函数 y = kx +(b – h )的图象. 可简记为“上加下减”.
总
结
x
y
–6 –4 –2 0 2 4 6
6
4
2
–2
–4
–6
y = 3x + 2
而当 b 相同,k 不相
同时(如 y = 3x + 2 与 y =
x + 2 )有:
共同点:_________________
不同点:_____________
两直线不平行
与 y 轴交于同一点
1
2
例 1 分别在同一个平面直角坐示系中画出下列函数的图象:
(1)y = 2x 与 y = 2x + 3;
(2)y = 2x + 1 与 y = x + 1;
1
2
x
y
y = 2x
y = 2x + 2
(1)y = 2x 与 y = 2x + 3;
x
y
y = 2x + 1
y = x + 1
1
2
(2)y = 2x + 1 与 y = x + 1;
1
2
练习
在同一平面直角坐标系中画出下列函数的图象,并说出它们有什么关系:
(1)y = – 2x;(2)y = – 2x – 4.
x
y
y = – 2x
y = – 2x – 4
y = – 2x 沿 y 轴向下平移 4 个单位得到 y = – 2x – 4.
课堂小结
一次函数 y = kx + b (k ≠ 0)的图象是一条直线.
随堂演练
1. 一次函数 y = x + 2 的图象大致是( )
A
B
C
D
A
2. 填空:
(1)将直线 y = 3x 向下平移 2 个单位,得到直线_____________.
(2)将直线 y = – x – 5 向上平移 5 个单位,得到直线_______________.
y = 3x – 2
y = – x
3. 在同一平面直角坐标系中画出下列函数图象.
x
y
(1)y = 2x;
(2)y = 2x + 3;
(3)y = x + 3
y = 2x
y = 2x
y = x + 3
课后作业
1.从教材习题中选取;
2.完成练习册本课时的习题.
华东师大版八年级数学下册
2 一次函数的图象
新课导入
我们已经学习了用描点法画函数的图象,也知道通常可以结合图象研究函数的性质和应用. 那么,一次函数的图象是什么形状呢?
新课探索
做
一
做
在同一平面坐标系中画出下列函数的图象:
(1)y = x;
1
2
(2)y = x + 2;
1
2
(3)y = 3x;
(4)y = 3x + 2;
(1)y = x;
1
2
x
–2
0
2
y
–1
0
1
x
y
–6 –4 –2 0 2 4 6
6
4
2
–2
–4
–6
(2)y = x + 2;
1
2
x
–2
0
2
y
1
2
3
x
y
–6 –4 –2 0 2 4 6
6
4
2
–2
–4
–6
x
y
–6 –4 –2 0 2 4 6
6
4
2
–2
–4
–6
(3)y = 3x;
x
–1
0
1
y
–3
0
3
y = 3x
x
y
–6 –4 –2 0 2 4 6
6
4
2
–2
–4
–6
(4)y = 3x + 2;
x
–1
0
1
y
–1
2
5
y = 3x
y = 3x + 2
x
y
–6 –4 –2 0 2 4 6
6
4
2
–2
–4
–6
y = 3x
y = 3x + 2
观察所画出的这些一次函数的图象,你能发现什么?
一次函数 y = kx + b (k ≠ 0)的图象是一条直线. 通常也称为直线 y = kx + b. 特别地,正比例函数 y = kx(k ≠ 0) 的图象是经过原点(0,0)的一条直线.
两点确定一条直线,画一次函数时,只需要取两个点.
讨论
观察“做一做”中画出的四个一次函数的图象,比较下列各对一次函数的图象有什么共同点,有什么不同点:
(1)y = 3x 与 y = 3x + 2;
(2)y = x 与 y = x + 2;
1
2
1
2
(3)y = 3x + 2 与 y = x + 2;
1
2
x
y
–6 –4 –2 0 2 4 6
6
4
2
–2
–4
–6
y = 3x
y = 3x + 2
两个一次函数,当系
数 k 相同,b 不相同时(如
y = 3x 与 y = 3x + 2 )有:
共同点:___________
不同点:_______________
两直线平行
与 y 轴交点不同
x
y
–6 –4 –2 0 2 4 6
6
4
2
–2
–4
–6
y = 3x
y = 3x + 2
由图看出 y = 3x + 2 可以由 y = 3x 沿 y 轴向上平移 2 个单位得到.
y = x + 2 可以由 y = x 沿 y 轴向上平移 2 个单位得到.
1
2
1
2
由正比例函数 y = kx + b 的图象向上平移 h(h > 0)个单位,可得一次函数 y = kx +(b + h)的图象;
由正比例函数 y = kx + b 的图象向下平移 h(h > 0)个单位,可得一次函数 y = kx +(b – h )的图象. 可简记为“上加下减”.
总
结
x
y
–6 –4 –2 0 2 4 6
6
4
2
–2
–4
–6
y = 3x + 2
而当 b 相同,k 不相
同时(如 y = 3x + 2 与 y =
x + 2 )有:
共同点:_________________
不同点:_____________
两直线不平行
与 y 轴交于同一点
1
2
例 1 分别在同一个平面直角坐示系中画出下列函数的图象:
(1)y = 2x 与 y = 2x + 3;
(2)y = 2x + 1 与 y = x + 1;
1
2
x
y
y = 2x
y = 2x + 2
(1)y = 2x 与 y = 2x + 3;
x
y
y = 2x + 1
y = x + 1
1
2
(2)y = 2x + 1 与 y = x + 1;
1
2
练习
在同一平面直角坐标系中画出下列函数的图象,并说出它们有什么关系:
(1)y = – 2x;(2)y = – 2x – 4.
x
y
y = – 2x
y = – 2x – 4
y = – 2x 沿 y 轴向下平移 4 个单位得到 y = – 2x – 4.
课堂小结
一次函数 y = kx + b (k ≠ 0)的图象是一条直线.
随堂演练
1. 一次函数 y = x + 2 的图象大致是( )
A
B
C
D
A
2. 填空:
(1)将直线 y = 3x 向下平移 2 个单位,得到直线_____________.
(2)将直线 y = – x – 5 向上平移 5 个单位,得到直线_______________.
y = 3x – 2
y = – x
3. 在同一平面直角坐标系中画出下列函数图象.
x
y
(1)y = 2x;
(2)y = 2x + 3;
(3)y = x + 3
y = 2x
y = 2x
y = x + 3
课后作业
1.从教材习题中选取;
2.完成练习册本课时的习题.
