华师大版数学八年级下册17.3.3.一次函数的性质 课件(共22张PPT)
文档属性
| 名称 | 华师大版数学八年级下册17.3.3.一次函数的性质 课件(共22张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 752.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-15 13:06:04 | ||
图片预览



文档简介
3 一次函数的性质
华东师大版八年级数学下册
新课导入
1. 一次函数的一般式.
y = kx + b
(k,b 为常数,k ≠ 0)
2. 一次函数的图象是什么?
一条直线.
新课探索
x
y
–1 1
–1
–1
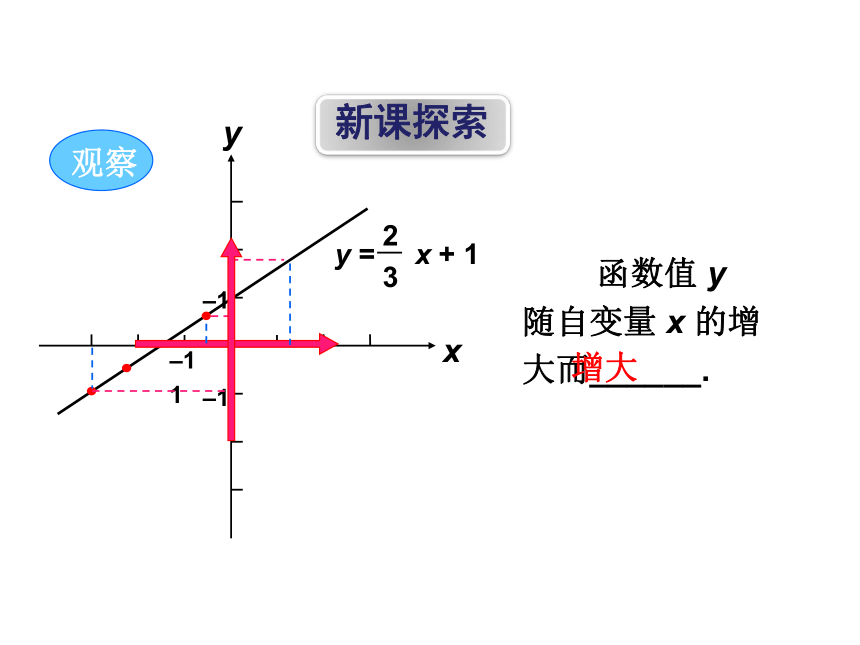
y = x + 1
2
3
函数值 y 随自变量 x 的增大而______.
增大
观察
x
y
–1 1
–1
–1
y = x + 1
2
3
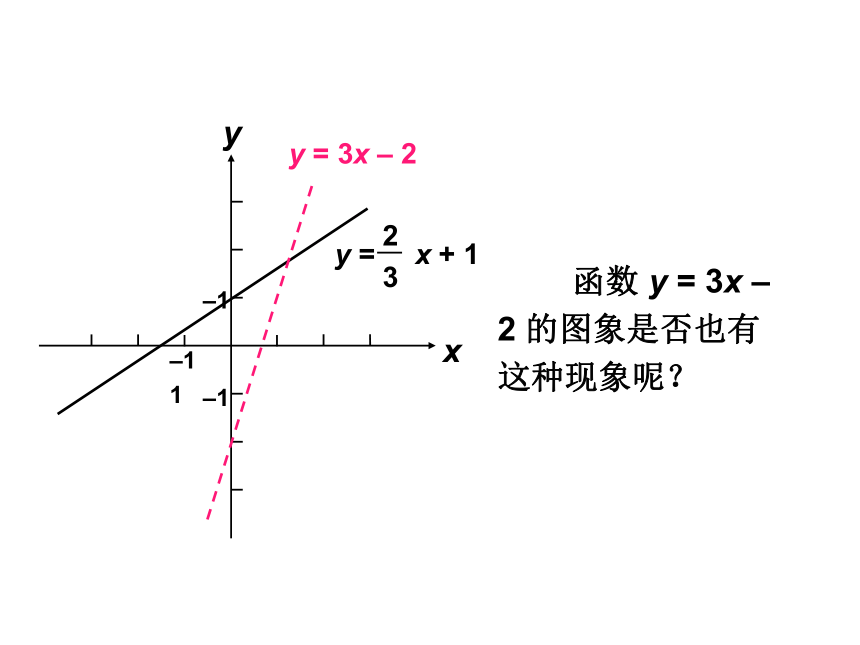
函数 y = 3x – 2 的图象是否也有这种现象呢?
y = 3x – 2
x
y
–1 1
–1
–1
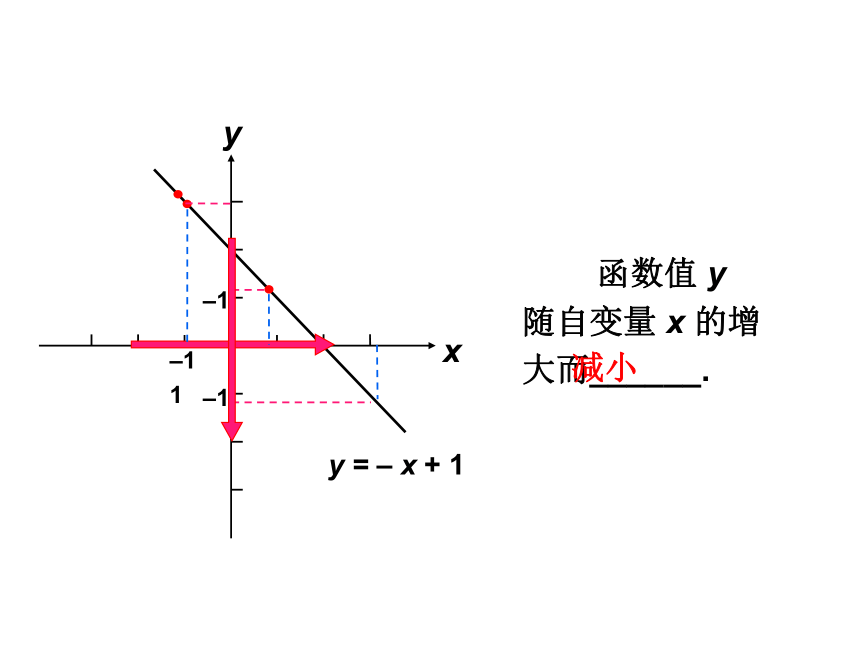
y = – x + 1
函数值 y 随自变量 x 的增大而______.
减小
x
y
–1 1
–1
–1
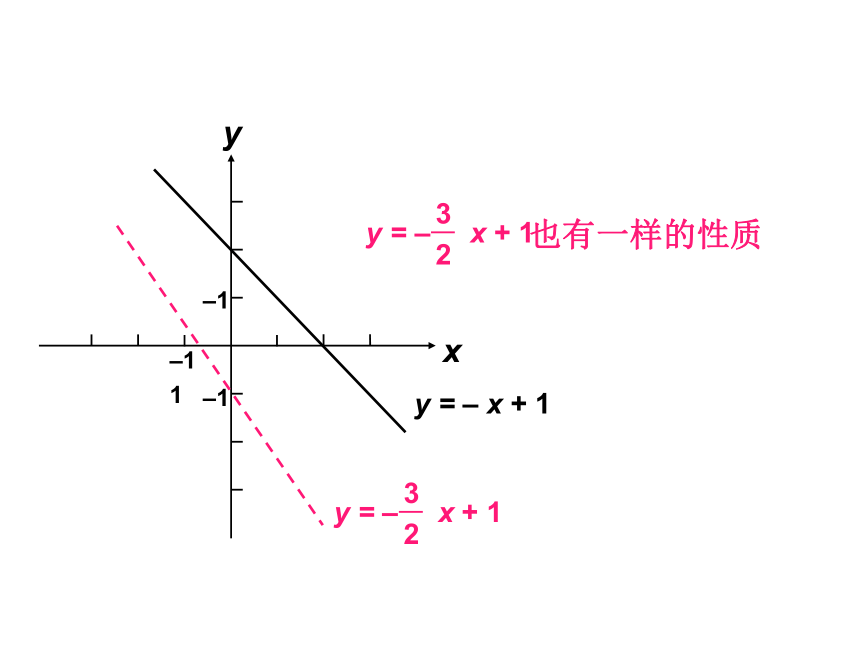
y = – x + 1
y = – x + 1
3
2
y = – x + 1
3
2
也有一样的性质
一次函数 y = kx + b 有下列性质:
(1)当 k>0 时,y 随 x 的增大而增大,这时函数的图象从左到右上升;
(2)当 k<0 时,y 随 x 的增大而______,这时函数的图象从左到右______.
减小
下降
概括
做
一
做
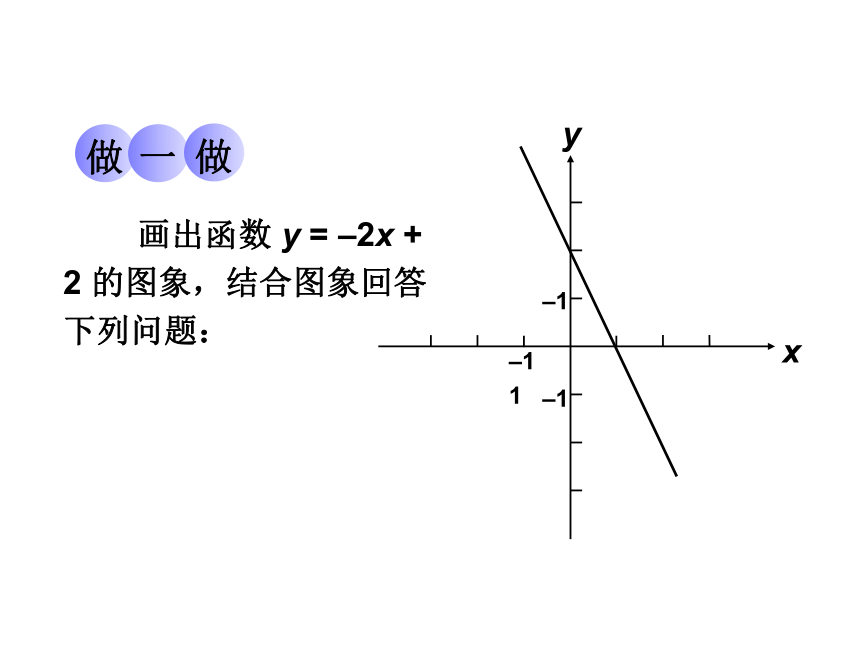
画出函数 y = –2x + 2 的图象,结合图象回答下列问题:
x
y
–1 1
–1
–1
x
y
–1 1
–1
–1
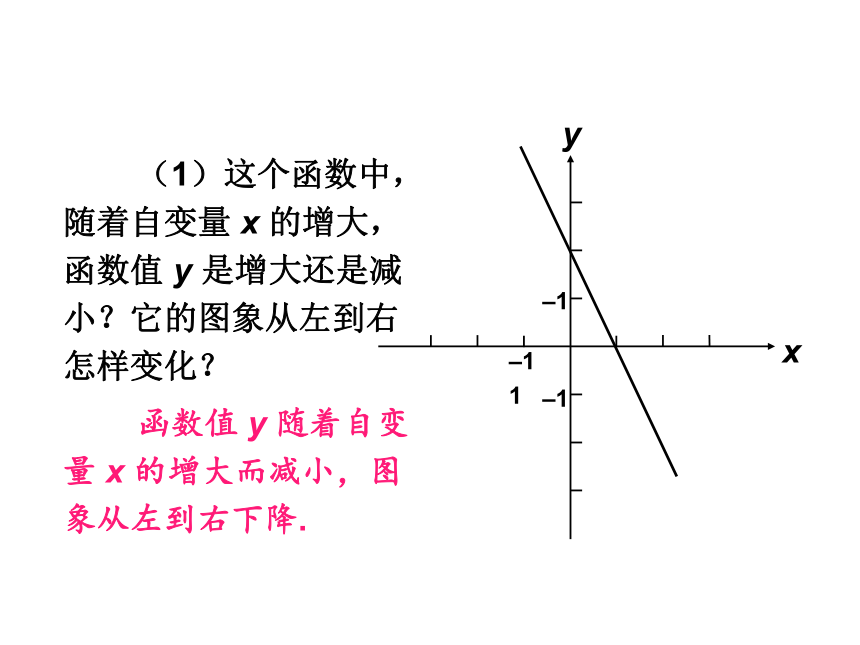
(1)这个函数中,随着自变量 x 的增大,函数值 y 是增大还是减小?它的图象从左到右怎样变化?
函数值 y 随着自变量 x 的增大而减小,图象从左到右下降.
(2)当 x 取何值时,y = 0?
x
y
–1 1
–1
–1
由图象可知,当 x = 1 时,y = 0.
(3)当 x 取何值时,y>0?
x
y
–1 1
–1
–1
由图象可知,当 x<1 时,y>0.
分别画出下面四个函数的图象.
y = x + 1
y = – x + 1
y = 2x + 1
y = – 2x + 1
y = kx + b
图象经过的象限
y 和 x 的变化
k>0
b > 0
b = 0
b < 0
k<0
b > 0
b = 0
b < 0
一、二、三
一、三
一、三、四
一、二、四
二、四
二、三、四
y 随 x 的增大
而增大
y 随 x 的增大
而减小
练习
已知函数 y =(m – 3)x – 3 (m 是常数), 回答下列问题:
(1)当 m 取何值时,y 随 x 的增大而增大?
(2)当 m 取何值时,y 随 x 的增大而减小?
解(1)当 m>3 时, y 随 x 的增大而增大.
(2)m<3 时, y 随 x 的增大而减小.
课堂小结
O
x
y
O
x
y
O
x
y
O
x
y
y = kx + b
k>0
b>0
k>0
b<0
k<0
b>0
k<0
b<0
随堂演练
1. 直线 y = 2x – 3 与 x 轴交点坐标为________,与 y 轴交点坐标为________,图象经过__________象限,y 随 x 的增大而________.
( ,0)
一、三、四
(0,– 3)
增大
2. 在同一直角坐标系中,对于函数:①y = – x – 1,②y = x + 1,③y = – x + 1,④y = – 2x – 1 的图象,下列说法不正确的是( )
A. 通过点(– 1,0)的是①和③
B. 两直线的交点在y轴负半轴上的是①和④
C. 相互平行的是①和③
D. 关于 y 轴对称的是②和③
A
3. 若A(– 3,y1),B(2,y2),C(3,y3)是函数 y = – x + 2 的图象上的点,则( )
A. y1<y2<y3 B. y1>y2>y3
C. y3<y1<y2 D. y2>y3>y1
B
4. 已知一次函数 y = (m + 2)x + m + 3 的图象与 y 轴的交点在 x 轴上方,且 y 随 x 的增大而减小,求 m 的取值范围.
m + 2<0
m + 3>0
解 由题意得
解得 – 2<m<– 3
5. 已知:一次函数 y = (2a + 4)x – (3 – b),当 a,b 为何值时:
(1)y 随 x 的增大而增大?
(2)图象经过第二、三、四象限?
(3)图象与 y 轴的交点在 x 轴上方?
解(1)由题意得
2a + 4>0,∴ a>– 2.
(2)由题意得
(3)由题意得
2a + 4<0
– (3 – b) <0
a<– 2
b<3
∴
2a + 4 ≠ 0
– (3 – b) >0
a ≠ – 2
b>3
∴
课后作业
1.从教材习题中选取;
2.完成练习册本课时的习题.
华东师大版八年级数学下册
新课导入
1. 一次函数的一般式.
y = kx + b
(k,b 为常数,k ≠ 0)
2. 一次函数的图象是什么?
一条直线.
新课探索
x
y
–1 1
–1
–1
y = x + 1
2
3
函数值 y 随自变量 x 的增大而______.
增大
观察
x
y
–1 1
–1
–1
y = x + 1
2
3
函数 y = 3x – 2 的图象是否也有这种现象呢?
y = 3x – 2
x
y
–1 1
–1
–1
y = – x + 1
函数值 y 随自变量 x 的增大而______.
减小
x
y
–1 1
–1
–1
y = – x + 1
y = – x + 1
3
2
y = – x + 1
3
2
也有一样的性质
一次函数 y = kx + b 有下列性质:
(1)当 k>0 时,y 随 x 的增大而增大,这时函数的图象从左到右上升;
(2)当 k<0 时,y 随 x 的增大而______,这时函数的图象从左到右______.
减小
下降
概括
做
一
做
画出函数 y = –2x + 2 的图象,结合图象回答下列问题:
x
y
–1 1
–1
–1
x
y
–1 1
–1
–1
(1)这个函数中,随着自变量 x 的增大,函数值 y 是增大还是减小?它的图象从左到右怎样变化?
函数值 y 随着自变量 x 的增大而减小,图象从左到右下降.
(2)当 x 取何值时,y = 0?
x
y
–1 1
–1
–1
由图象可知,当 x = 1 时,y = 0.
(3)当 x 取何值时,y>0?
x
y
–1 1
–1
–1
由图象可知,当 x<1 时,y>0.
分别画出下面四个函数的图象.
y = x + 1
y = – x + 1
y = 2x + 1
y = – 2x + 1
y = kx + b
图象经过的象限
y 和 x 的变化
k>0
b > 0
b = 0
b < 0
k<0
b > 0
b = 0
b < 0
一、二、三
一、三
一、三、四
一、二、四
二、四
二、三、四
y 随 x 的增大
而增大
y 随 x 的增大
而减小
练习
已知函数 y =(m – 3)x – 3 (m 是常数), 回答下列问题:
(1)当 m 取何值时,y 随 x 的增大而增大?
(2)当 m 取何值时,y 随 x 的增大而减小?
解(1)当 m>3 时, y 随 x 的增大而增大.
(2)m<3 时, y 随 x 的增大而减小.
课堂小结
O
x
y
O
x
y
O
x
y
O
x
y
y = kx + b
k>0
b>0
k>0
b<0
k<0
b>0
k<0
b<0
随堂演练
1. 直线 y = 2x – 3 与 x 轴交点坐标为________,与 y 轴交点坐标为________,图象经过__________象限,y 随 x 的增大而________.
( ,0)
一、三、四
(0,– 3)
增大
2. 在同一直角坐标系中,对于函数:①y = – x – 1,②y = x + 1,③y = – x + 1,④y = – 2x – 1 的图象,下列说法不正确的是( )
A. 通过点(– 1,0)的是①和③
B. 两直线的交点在y轴负半轴上的是①和④
C. 相互平行的是①和③
D. 关于 y 轴对称的是②和③
A
3. 若A(– 3,y1),B(2,y2),C(3,y3)是函数 y = – x + 2 的图象上的点,则( )
A. y1<y2<y3 B. y1>y2>y3
C. y3<y1<y2 D. y2>y3>y1
B
4. 已知一次函数 y = (m + 2)x + m + 3 的图象与 y 轴的交点在 x 轴上方,且 y 随 x 的增大而减小,求 m 的取值范围.
m + 2<0
m + 3>0
解 由题意得
解得 – 2<m<– 3
5. 已知:一次函数 y = (2a + 4)x – (3 – b),当 a,b 为何值时:
(1)y 随 x 的增大而增大?
(2)图象经过第二、三、四象限?
(3)图象与 y 轴的交点在 x 轴上方?
解(1)由题意得
2a + 4>0,∴ a>– 2.
(2)由题意得
(3)由题意得
2a + 4<0
– (3 – b) <0
a<– 2
b<3
∴
2a + 4 ≠ 0
– (3 – b) >0
a ≠ – 2
b>3
∴
课后作业
1.从教材习题中选取;
2.完成练习册本课时的习题.
