华师大版数学八年级下册17.1 变量与函数 课件(共28张PPT)
文档属性
| 名称 | 华师大版数学八年级下册17.1 变量与函数 课件(共28张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-15 00:00:00 | ||
图片预览




文档简介
17.1 变量与函数
第17章 函数及其图象
第1课时 变量与函数
新课导入
大千世界处在不停的运动变化中,如何来研究这些运动变化规律呢?数学上常用变量与函数来刻画各种运动变化.
新课探究
如图是某地一天内的气温变化图.
问题 1
0
2
4
6
8
-2
-4
2
4
6
8
10
12
14
16
18
20
22
24
气温T
(℃)
时间 t
(时)
这张图告诉我们哪些信息?
看图回答:
(1)这天的 6 时、10 时和 14 时的气温分别是多少?任意给出这天中的某一时刻,你能说出这一时刻的气温是多少吗?
0
2
4
6
8
-2
-4
2
4
6
8
10
12
14
16
18
20
22
24
气温T
(℃)
时间 t
(时)
-1℃
2℃
5℃
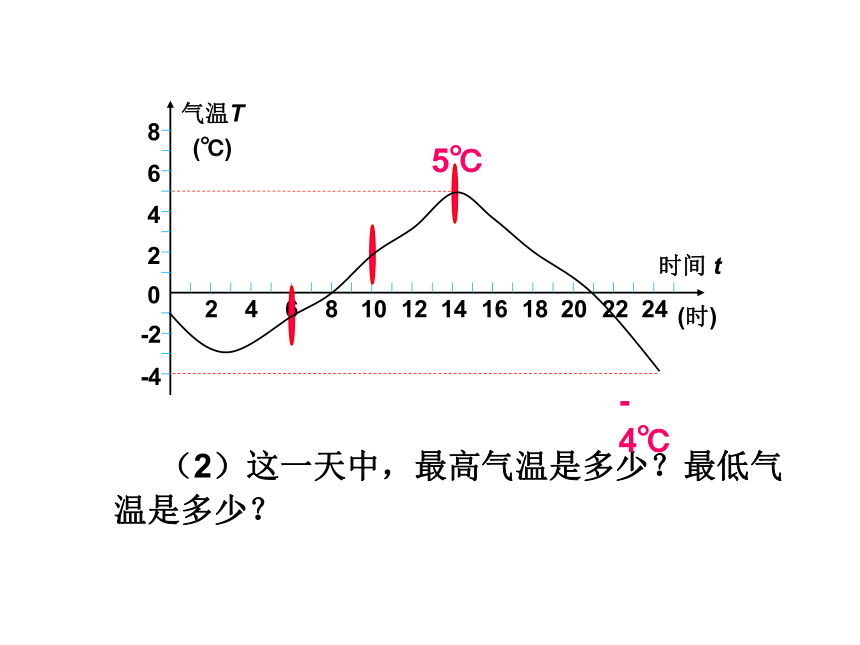
(2)这一天中,最高气温是多少?最低气温是多少?
0
2
4
6
8
-2
-4
2
4
6
8
10
12
14
16
18
20
22
24
气温T
(℃)
时间 t
(时)
5℃
-4℃
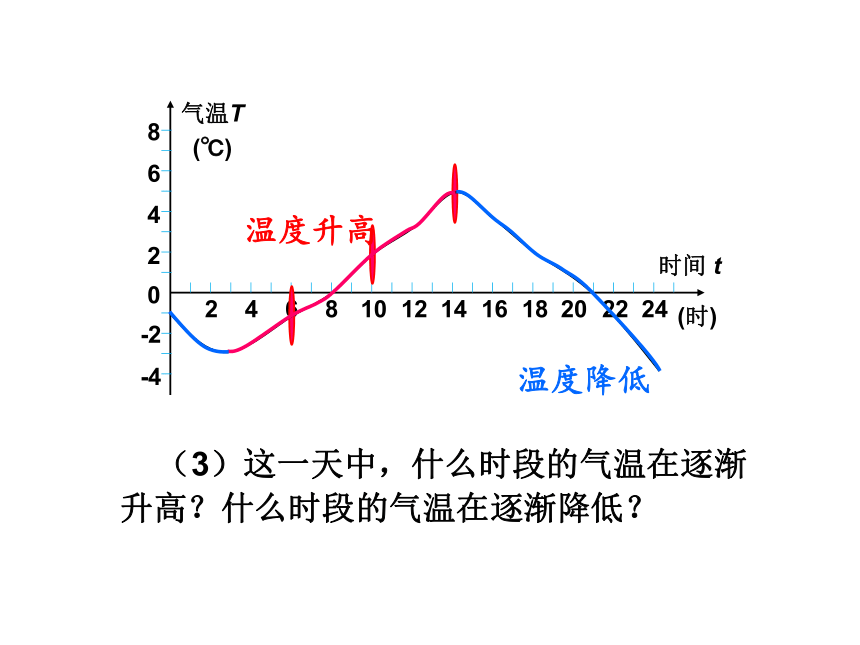
(3)这一天中,什么时段的气温在逐渐升高?什么时段的气温在逐渐降低?
0
2
4
6
8
-2
-4
2
4
6
8
10
12
14
16
18
20
22
24
气温T
(℃)
时间 t
(时)
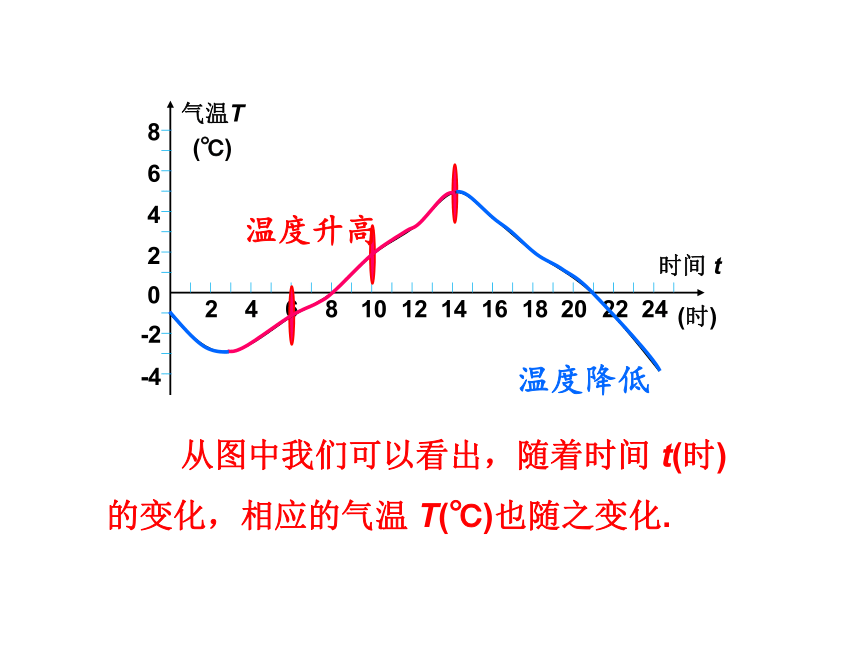
温度升高
温度降低
从图中我们可以看出,随着时间 t(时)的变化,相应的气温 T(℃)也随之变化.
0
2
4
6
8
-2
-4
2
4
6
8
10
12
14
16
18
20
22
24
气温T
(℃)
时间 t
(时)
温度升高
温度降低
问题 2
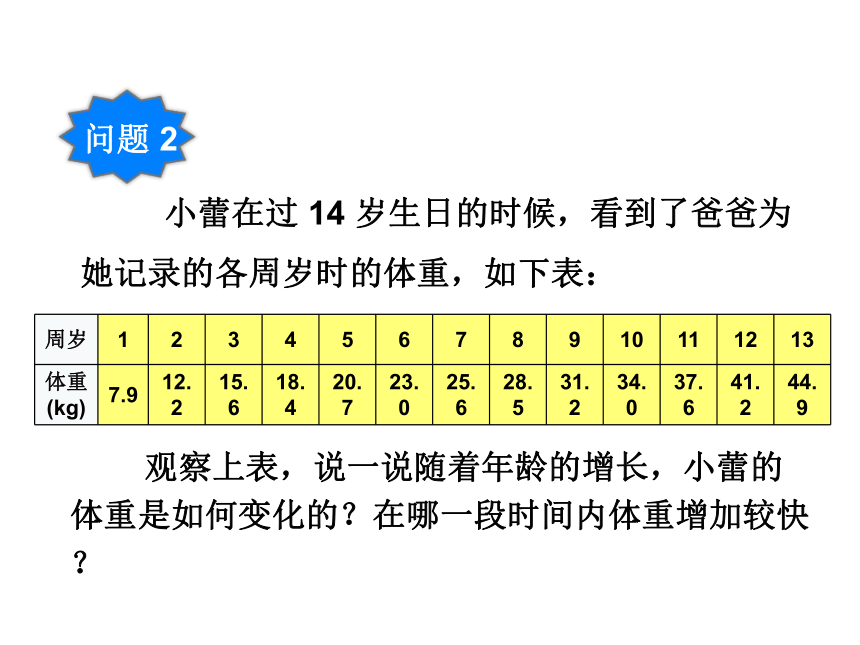
小蕾在过 14 岁生日的时候,看到了爸爸为她记录的各周岁时的体重,如下表:
周岁
1
2
3
4
5
6
7
8
9
10
11
12
13
体重(kg)
7.9
12.2
15.6
18.4
20.7
23.0
25.6
28.5
31.2
34.0
37.6
41.2
44.9
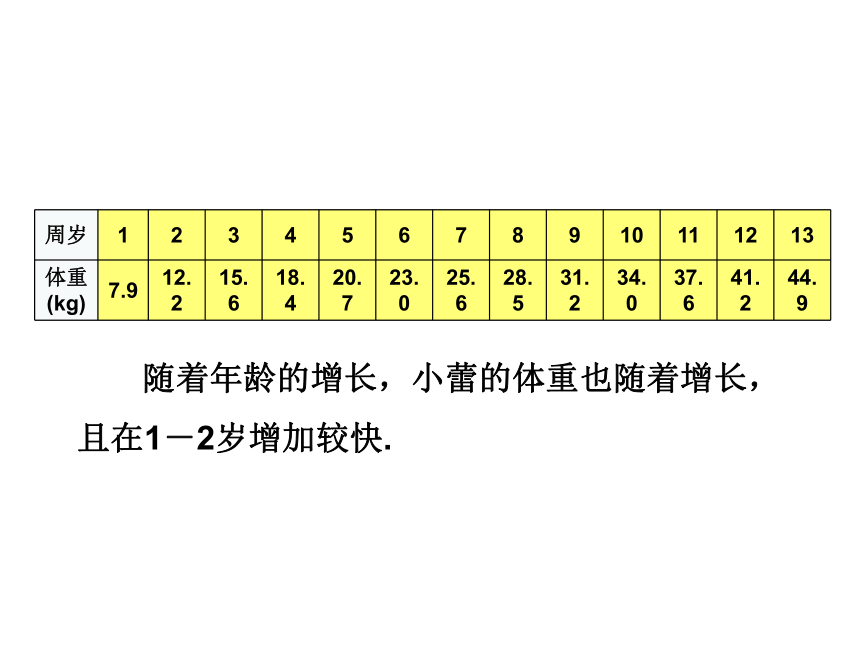
观察上表,说一说随着年龄的增长,小蕾的体重是如何变化的?在哪一段时间内体重增加较快?
周岁
1
2
3
4
5
6
7
8
9
10
11
12
13
体重(kg)
7.9
12.2
15.6
18.4
20.7
23.0
25.6
28.5
31.2
34.0
37.6
41.2
44.9
随着年龄的增长,小蕾的体重也随着增长,且在1-2岁增加较快.
问题 3
收音机上的刻度盘的波长和频率分别是用米(m)和千赫兹(kHz)为单位标刻的.下面是一些对应的数值:
波长 λ(m)
300
500
600
1000
1500
频率 f(kHz)
1000
600
500
300
200
波长 λ(m)
300
500
600
1000
1500
频率 f(kHz)
1000
600
500
300
200
细心的同学可能会发现:每一列 λ 与 f 的对应值的乘积是一个定值,即:
λ f = 300 000,
或者说
300 000
λ
f =
可以看出:波长 λ 越大,频率 f 就_______.
越小
圆的面积随着半径的增大而增大.如果用 r 表示圆的半径,S 表示圆的面积,则 S与r 之间满足下列关系:
S =________.
问题 4
πr2
半径r(cm)
1
1.5
2
2.6
3.2
…
圆面积S(cm2)
…
利用这个关系式,试求出半径为 1 cm、1.5 cm、2 cm、2.6 cm、3.2 cm 时圆的面积,并将结果填入下表:
π
2.25π
4π
6.76π
10.24π
在上面的问题中,我们研究了一些数量关系,它们都刻画了某些变化规律.这里出现了各种各样的量,特别值得注意的是出现了一些数值会发生变化的量.
概括
例如问题1 中,刻画气温变化规律的量是时间 t 和气温 T,气温 T 随着时间 t 的变化而变化,它们可以取不同的数值.
像这样在某一变化过程中,可以取不同数值的量,叫做变量.
在其他三个问题中,有哪些变量?
问题2 年龄和体重是变量;
问题3 波长 λ 和频率 f 是变量;
问题4 面积 S 和半径 r 是变量.
上面的各个问题中,都出现了两个变量,它们互相依赖,密切相关.
一般地,如果在一个变化过程中,有两个变量,例如 x 和 y ,对于 x 的每一个值,y 都有唯一的值与之对应,我们就说 x 是自变量,y 是因变量,此时也称 y 是 x 的函数.
表示函数关系的方法通常有三种:
(1)解析法. 如问题 3 中的 ,问题 4 中的 S = πr2,函数关系是用表达式表示的,它们又称函数关系式.
300 000
λ
f =
(2)列表法. 如问题 2 中的小蕾的体重表,问题 3 中的波长与频率关系表.
周岁
1
2
3
4
5
6
7
8
9
10
11
12
13
体重(kg)
7.9
12.2
15.6
18.4
20.7
23.0
25.6
28.5
31.2
34.0
37.6
41.2
44.9
波长 λ(m)
300
500
600
1000
1500
频率 f(kHz)
1000
600
500
300
200
(3)图象法. 如问题 1 中的气温曲线.
在问题的研究过程中,还有一种量,它的取值始终保持不变,我们称之为常量,
例如圆的周长 l = 2πr (其中 l 为周长,r 为半径).
2π 是常量
在研究函数时,必须注意自变量的取值范围.实际问题中,自变量的取值必须符合实际意义.
例如,上述问题4 中,自变量 r 表示圆的半径,不能为负数和零,即它的取值范围是一切正实数.
r
1. 举出 3 个日常生活中遇到的变量与函数的例子.
练 习
2.下表是某城市 2012 年统计的中小学男生各年龄组的平均身高:
年龄组(岁)
7
8
9
10
11
12
13
14
15
16
17
18
平均身高(cm)
117
121
125
130
135
142
148
155
162
167
170
172
观察此表,回答下列问题:
(1)该市14岁男学生的平均身高是多少?
年龄组(岁)
7
8
9
10
11
12
13
14
15
16
17
18
平均身高(cm)
117
121
125
130
135
142
148
155
162
167
170
172
(2)该市男学生的平均身高从哪一岁开始增加特别迅速?
4
4
5
5
7
6
7
7
5
3
2
年龄组(岁)
7
8
9
10
11
12
13
14
15
16
17
18
平均身高(cm)
117
121
125
130
135
142
148
155
162
167
170
172
(3)这里反映了哪些变量之间的关系?其中哪个是自变量?哪个是因变量?
反映了年龄与身高之间的关系;年龄是自变量,身高是因变量.
课堂小结
一般地,如果在一个变化过程中,有两个变量,例如 x 和 y ,对于 x 的每一个值,y 都有唯一的值与之对应,我们就说 x 是自变量,y 是因变量,此时也称 y 是 x 的函数.
1.从教材习题中选取;
2.完成练习册本课时的习题.
课后作业
第17章 函数及其图象
第1课时 变量与函数
新课导入
大千世界处在不停的运动变化中,如何来研究这些运动变化规律呢?数学上常用变量与函数来刻画各种运动变化.
新课探究
如图是某地一天内的气温变化图.
问题 1
0
2
4
6
8
-2
-4
2
4
6
8
10
12
14
16
18
20
22
24
气温T
(℃)
时间 t
(时)
这张图告诉我们哪些信息?
看图回答:
(1)这天的 6 时、10 时和 14 时的气温分别是多少?任意给出这天中的某一时刻,你能说出这一时刻的气温是多少吗?
0
2
4
6
8
-2
-4
2
4
6
8
10
12
14
16
18
20
22
24
气温T
(℃)
时间 t
(时)
-1℃
2℃
5℃
(2)这一天中,最高气温是多少?最低气温是多少?
0
2
4
6
8
-2
-4
2
4
6
8
10
12
14
16
18
20
22
24
气温T
(℃)
时间 t
(时)
5℃
-4℃
(3)这一天中,什么时段的气温在逐渐升高?什么时段的气温在逐渐降低?
0
2
4
6
8
-2
-4
2
4
6
8
10
12
14
16
18
20
22
24
气温T
(℃)
时间 t
(时)
温度升高
温度降低
从图中我们可以看出,随着时间 t(时)的变化,相应的气温 T(℃)也随之变化.
0
2
4
6
8
-2
-4
2
4
6
8
10
12
14
16
18
20
22
24
气温T
(℃)
时间 t
(时)
温度升高
温度降低
问题 2
小蕾在过 14 岁生日的时候,看到了爸爸为她记录的各周岁时的体重,如下表:
周岁
1
2
3
4
5
6
7
8
9
10
11
12
13
体重(kg)
7.9
12.2
15.6
18.4
20.7
23.0
25.6
28.5
31.2
34.0
37.6
41.2
44.9
观察上表,说一说随着年龄的增长,小蕾的体重是如何变化的?在哪一段时间内体重增加较快?
周岁
1
2
3
4
5
6
7
8
9
10
11
12
13
体重(kg)
7.9
12.2
15.6
18.4
20.7
23.0
25.6
28.5
31.2
34.0
37.6
41.2
44.9
随着年龄的增长,小蕾的体重也随着增长,且在1-2岁增加较快.
问题 3
收音机上的刻度盘的波长和频率分别是用米(m)和千赫兹(kHz)为单位标刻的.下面是一些对应的数值:
波长 λ(m)
300
500
600
1000
1500
频率 f(kHz)
1000
600
500
300
200
波长 λ(m)
300
500
600
1000
1500
频率 f(kHz)
1000
600
500
300
200
细心的同学可能会发现:每一列 λ 与 f 的对应值的乘积是一个定值,即:
λ f = 300 000,
或者说
300 000
λ
f =
可以看出:波长 λ 越大,频率 f 就_______.
越小
圆的面积随着半径的增大而增大.如果用 r 表示圆的半径,S 表示圆的面积,则 S与r 之间满足下列关系:
S =________.
问题 4
πr2
半径r(cm)
1
1.5
2
2.6
3.2
…
圆面积S(cm2)
…
利用这个关系式,试求出半径为 1 cm、1.5 cm、2 cm、2.6 cm、3.2 cm 时圆的面积,并将结果填入下表:
π
2.25π
4π
6.76π
10.24π
在上面的问题中,我们研究了一些数量关系,它们都刻画了某些变化规律.这里出现了各种各样的量,特别值得注意的是出现了一些数值会发生变化的量.
概括
例如问题1 中,刻画气温变化规律的量是时间 t 和气温 T,气温 T 随着时间 t 的变化而变化,它们可以取不同的数值.
像这样在某一变化过程中,可以取不同数值的量,叫做变量.
在其他三个问题中,有哪些变量?
问题2 年龄和体重是变量;
问题3 波长 λ 和频率 f 是变量;
问题4 面积 S 和半径 r 是变量.
上面的各个问题中,都出现了两个变量,它们互相依赖,密切相关.
一般地,如果在一个变化过程中,有两个变量,例如 x 和 y ,对于 x 的每一个值,y 都有唯一的值与之对应,我们就说 x 是自变量,y 是因变量,此时也称 y 是 x 的函数.
表示函数关系的方法通常有三种:
(1)解析法. 如问题 3 中的 ,问题 4 中的 S = πr2,函数关系是用表达式表示的,它们又称函数关系式.
300 000
λ
f =
(2)列表法. 如问题 2 中的小蕾的体重表,问题 3 中的波长与频率关系表.
周岁
1
2
3
4
5
6
7
8
9
10
11
12
13
体重(kg)
7.9
12.2
15.6
18.4
20.7
23.0
25.6
28.5
31.2
34.0
37.6
41.2
44.9
波长 λ(m)
300
500
600
1000
1500
频率 f(kHz)
1000
600
500
300
200
(3)图象法. 如问题 1 中的气温曲线.
在问题的研究过程中,还有一种量,它的取值始终保持不变,我们称之为常量,
例如圆的周长 l = 2πr (其中 l 为周长,r 为半径).
2π 是常量
在研究函数时,必须注意自变量的取值范围.实际问题中,自变量的取值必须符合实际意义.
例如,上述问题4 中,自变量 r 表示圆的半径,不能为负数和零,即它的取值范围是一切正实数.
r
1. 举出 3 个日常生活中遇到的变量与函数的例子.
练 习
2.下表是某城市 2012 年统计的中小学男生各年龄组的平均身高:
年龄组(岁)
7
8
9
10
11
12
13
14
15
16
17
18
平均身高(cm)
117
121
125
130
135
142
148
155
162
167
170
172
观察此表,回答下列问题:
(1)该市14岁男学生的平均身高是多少?
年龄组(岁)
7
8
9
10
11
12
13
14
15
16
17
18
平均身高(cm)
117
121
125
130
135
142
148
155
162
167
170
172
(2)该市男学生的平均身高从哪一岁开始增加特别迅速?
4
4
5
5
7
6
7
7
5
3
2
年龄组(岁)
7
8
9
10
11
12
13
14
15
16
17
18
平均身高(cm)
117
121
125
130
135
142
148
155
162
167
170
172
(3)这里反映了哪些变量之间的关系?其中哪个是自变量?哪个是因变量?
反映了年龄与身高之间的关系;年龄是自变量,身高是因变量.
课堂小结
一般地,如果在一个变化过程中,有两个变量,例如 x 和 y ,对于 x 的每一个值,y 都有唯一的值与之对应,我们就说 x 是自变量,y 是因变量,此时也称 y 是 x 的函数.
1.从教材习题中选取;
2.完成练习册本课时的习题.
课后作业
