2.1.2合情推理-类比推理
图片预览







文档简介
(共28张PPT)
2.从1=1, 1-4=-(1+2), 1-4+9=1+2+3, 1-4+9-16=-(1+2+3+4), …… , 概括出第n个式子___________ .
作业1
1-4+9 +…… +(-1)n+1n2=(-1)n+1(1+2+3+……+n)
5.观察直线上n个点, 发现两个点确定1条线段, 三个点确定3条线段, 四个点可以确定6条线段, 五个点可以确定10条线段, 由此可以归纳出什么规律
作业1
9.对于怎样的自然数n , 有不等式2n>n2成立 (不需要证明)
作业1
2、归纳推理的一般模式:
S1具有P,
S2具有P,
……
Sn具有P,
(S1,S2,…,Sn是A类事物的对象)
所以A类事物具有P
1、什么是归纳推理?
复习回顾
从 中推演出
的推理,通常称为归纳推理.
个别事实
一般性的结论
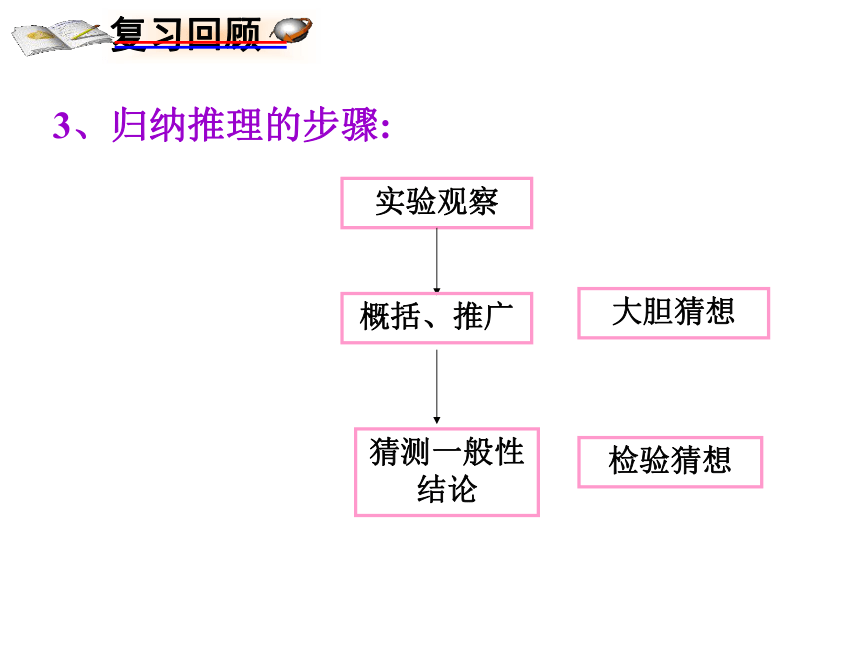
3、归纳推理的步骤:
实验观察
概括、推广
猜测一般性结论
复习回顾
大胆猜想
检验猜想
没有大胆的猜想,
就作不出伟大的发现 。
--牛顿
问题情境
推理案例1 前提:矩形的对角线的平方等于长、宽的平方和. 结论:长方体的对角线的平方等于长、宽、高的平方和.
合情推理—类比推理
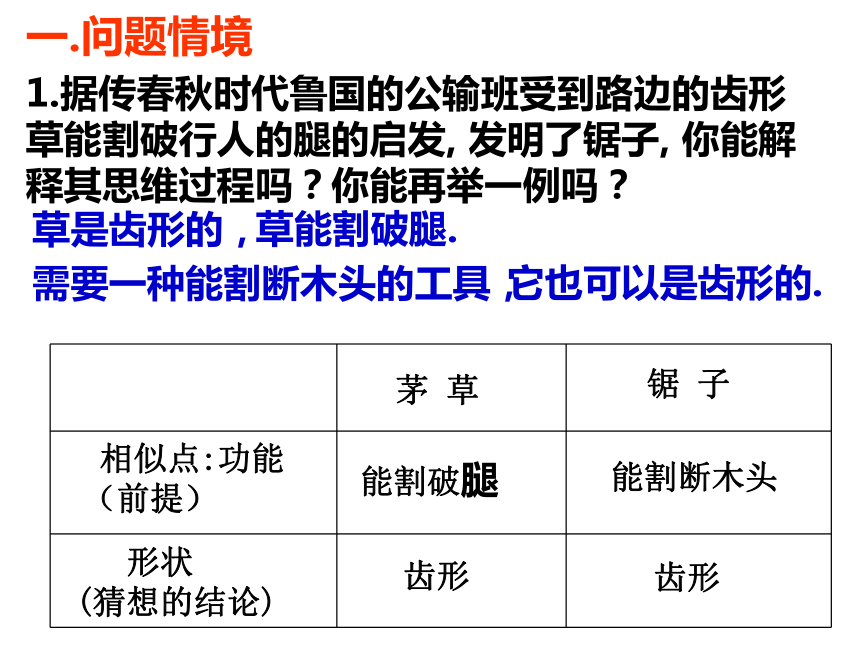
草是齿形的,
草能割破腿.
需要一种能割断木头的工具,
它也可以是齿形的.
一.问题情境
1.据传春秋时代鲁国的公输班受到路边的齿形草能割破行人的腿的启发, 发明了锯子, 你能解释其思维过程吗?你能再举一例吗?
相似点:功能
(前提)
形状
(猜想的结论)
能割破腿
能割断木头
齿形
齿形
茅 草
锯 子
利用平面向量的基本定理类比得到空间向量的基本定理.
可能有生命存在
有生命存在
温度适合生物的生存
一年中有四季的变更
有大气层
大部分时间的温度适合地球上某些已知生物的生存
一年中有四季的变更
有大气层
行星、围绕太阳运行、绕轴自转
行星、围绕太阳运行、绕轴自转
火星
地球
探究二:火星上是否存在生命
仿照鱼类的外型和它们在水中沉浮的原理,发明了潜水艇.
火星与地球类比的思维过程:
火星
地球
存在类似特征
地球上有生命存在
猜测火星上也可能有生命存在
2.试根据等式的性质猜想不等式的性质。
等式的性质:
(1) a=b a+c=b+c;
(2) a=b ac=bc;
(3) a=b a2=b2;等等。
猜想不等式的性质:
(1) a>b a+c>b+c;
(2) a>b ac>bc;
(3) a>b a2>b2;等等。
问:这样猜想出的结论是否一定正确?
由两个(两类)对象之间在某些方面的相似或 相同,推演出他们在其他方面也相似或相同, 像这样的推理称为类比推理(简称类比法)
二.数学建构
1、定义:
2、思维过程:
观察、比较
联想、类推
猜想新结论
3.类比推理的几个特点;
1.类比是从人们已经掌握了的事物的属性,推测正在研究的事物的属性,是以旧有的认识为基础,类比出新的结果.
2.类比是从一种事物的特殊属性推测另一种事物的特殊属性.
3.类比的结果是猜测性的不一定可靠,但它却有发现的功能.
特点:
(1)特殊到特殊
(2)猜测性(类比的结论不一定正确)
例1.类比实数的加法与乘法,并列出它们类似的性质.
加法性质
乘法性质
a+b=b+a
(a+b)+c=a+(b+c)
a+ (-a)=0
a+0=a
ab=ba
(ab)c=a(bc)
类比元素:
加法
乘法
减法
(和 积)
除法
(差 商)
负数
倒数
例2.试将平面上的圆与空间的球进行类比.
圆的定义:平面内到一个定点的距离等于定长的点的集合.
球的定义:到一个定点的距离等于定长的点的集合.
弦
直径周长
面积
截面圆
大圆
表面积
体积
类比元素:
球
类比对象:
圆
圆的性质 球的性质
圆心与弦(不是直径)的中点的连线垂直于弦
与圆心距离相等的两弦相等;与圆心距离不等的两弦不等,距圆心较近的弦较长
圆的切线垂直于过切点的半径;经过圆心且垂直于切线的直线必经过切点
经过切点且垂直于切线的直线必经过圆心
球心与截面圆(不是大圆)的圆心的连线垂直于截面圆
与球心距离相等的两截面圆相等;与球心距离不等的两截面圆不等,距球心较近的截面圆较大
球的切面垂直于过切点的半径;经过球心且垂直于切面的直线必经过切点
经过切点且垂直于切面的直线必经过球心
例3.(1)类比平面直角三角形的勾股定理, 试给出立体几何中类似的结论.
类比对象:
三角形
四面体
直角三角形
有三个面两两垂直的四面体
直角三角形
∠C=90°
3个边的长度a,b,c
2条直角边a,b和1条斜边c
3个面两两垂直的四面体
∠PDF=∠PDE=∠EDF=90°
4个面的面积S1,S2,S3和S
3个“直角面” S1,S2,S3和1个“斜面” S
例3.(2)在空间中与“等边三角形内任意一点P到三边的距离之和等于三角形的高”相类似的结论是什么?
类比对象:
正三角形
正四面体
正四面体内任一点到四个面的距离和等于正四面体的高.
类比推理的一般步骤:
(1)寻找合适的类比对象
(常已给出)
(2)找出两类对象之间可以确切表述的相似
特征;
(3)用一类对象的已知特征去推测另一类对
象的特征,从而得出一个猜想;
(4)检验猜想,即证明。
例4.已知: 等差数列{an}的公差为d , 前n项和为Sn , 有如下性质:
(1)an=am+(n-m)d
(2)若m+n=p+q , 其中m , n , p , q∈N*, 则am+an=ap+aq
(3)若m+n=2p , m , n , p∈N*, 则am+an=2ap
(4)Sn , S2n-Sn , S3n-S2n构成等差数列
类比上述性质, 在等比数列{bn}中, 写出相类似的性质.
等差数列 等比数列
定义
通项公式
前n项和
例1、利用等差数列性质类比等比数列性质
等差数列 等比数列
中项
性质
n+m=p+q时,
am+an= ap+aq
n+m=p+q时,
aman= apaq
任意实数a、b都有等差中项 ,为
当且仅当a、b同号时才有等比中项 ,为
成等差数列
成等比数列
下标等差,项等差
下标等差,项等比
课堂练习
1.作业7.平面中的三角形和空间四面体有着许多相类似的性质, 例如在三角形中:
(1)三角形两边之和大于第三边;
(2) S△= 底×高;
(3)三角形的中位线平行于第三边且等于第三
边的一半.
……那么在空间四面体中相应的结论是什么?
2.作业4.已知等差数列有一性质: 若 是等差数列,则通项 为的数列也是等差数列.类比上述命题,相应的等比数列有性质:若 是等比数列( ),则通项 = 的数列也是等比数列
练习1(2004广东,15)
由图(1)有面积关系:
则由图(2)有体积关系:
图(1)
图(2)
五、课堂小结:
1、运用类比方法解决问题,其基本过程可用框图
表示如下:
原问题
类比问题
原问题解法
类比问题的解法
2、运用类比法的关键是:寻找一个合适的类比对象。
几何中常见的类比对象
三角形
四面体(各面均为三角形)
四边形
六面体(各面均为四边形)
圆
球
代数中常见的类比对象
数
向量
方程
函数
不等式
交集,并集,补集
或,且,非运算
无限
有限
2.从1=1, 1-4=-(1+2), 1-4+9=1+2+3, 1-4+9-16=-(1+2+3+4), …… , 概括出第n个式子___________ .
作业1
1-4+9 +…… +(-1)n+1n2=(-1)n+1(1+2+3+……+n)
5.观察直线上n个点, 发现两个点确定1条线段, 三个点确定3条线段, 四个点可以确定6条线段, 五个点可以确定10条线段, 由此可以归纳出什么规律
作业1
9.对于怎样的自然数n , 有不等式2n>n2成立 (不需要证明)
作业1
2、归纳推理的一般模式:
S1具有P,
S2具有P,
……
Sn具有P,
(S1,S2,…,Sn是A类事物的对象)
所以A类事物具有P
1、什么是归纳推理?
复习回顾
从 中推演出
的推理,通常称为归纳推理.
个别事实
一般性的结论
3、归纳推理的步骤:
实验观察
概括、推广
猜测一般性结论
复习回顾
大胆猜想
检验猜想
没有大胆的猜想,
就作不出伟大的发现 。
--牛顿
问题情境
推理案例1 前提:矩形的对角线的平方等于长、宽的平方和. 结论:长方体的对角线的平方等于长、宽、高的平方和.
合情推理—类比推理
草是齿形的,
草能割破腿.
需要一种能割断木头的工具,
它也可以是齿形的.
一.问题情境
1.据传春秋时代鲁国的公输班受到路边的齿形草能割破行人的腿的启发, 发明了锯子, 你能解释其思维过程吗?你能再举一例吗?
相似点:功能
(前提)
形状
(猜想的结论)
能割破腿
能割断木头
齿形
齿形
茅 草
锯 子
利用平面向量的基本定理类比得到空间向量的基本定理.
可能有生命存在
有生命存在
温度适合生物的生存
一年中有四季的变更
有大气层
大部分时间的温度适合地球上某些已知生物的生存
一年中有四季的变更
有大气层
行星、围绕太阳运行、绕轴自转
行星、围绕太阳运行、绕轴自转
火星
地球
探究二:火星上是否存在生命
仿照鱼类的外型和它们在水中沉浮的原理,发明了潜水艇.
火星与地球类比的思维过程:
火星
地球
存在类似特征
地球上有生命存在
猜测火星上也可能有生命存在
2.试根据等式的性质猜想不等式的性质。
等式的性质:
(1) a=b a+c=b+c;
(2) a=b ac=bc;
(3) a=b a2=b2;等等。
猜想不等式的性质:
(1) a>b a+c>b+c;
(2) a>b ac>bc;
(3) a>b a2>b2;等等。
问:这样猜想出的结论是否一定正确?
由两个(两类)对象之间在某些方面的相似或 相同,推演出他们在其他方面也相似或相同, 像这样的推理称为类比推理(简称类比法)
二.数学建构
1、定义:
2、思维过程:
观察、比较
联想、类推
猜想新结论
3.类比推理的几个特点;
1.类比是从人们已经掌握了的事物的属性,推测正在研究的事物的属性,是以旧有的认识为基础,类比出新的结果.
2.类比是从一种事物的特殊属性推测另一种事物的特殊属性.
3.类比的结果是猜测性的不一定可靠,但它却有发现的功能.
特点:
(1)特殊到特殊
(2)猜测性(类比的结论不一定正确)
例1.类比实数的加法与乘法,并列出它们类似的性质.
加法性质
乘法性质
a+b=b+a
(a+b)+c=a+(b+c)
a+ (-a)=0
a+0=a
ab=ba
(ab)c=a(bc)
类比元素:
加法
乘法
减法
(和 积)
除法
(差 商)
负数
倒数
例2.试将平面上的圆与空间的球进行类比.
圆的定义:平面内到一个定点的距离等于定长的点的集合.
球的定义:到一个定点的距离等于定长的点的集合.
弦
直径周长
面积
截面圆
大圆
表面积
体积
类比元素:
球
类比对象:
圆
圆的性质 球的性质
圆心与弦(不是直径)的中点的连线垂直于弦
与圆心距离相等的两弦相等;与圆心距离不等的两弦不等,距圆心较近的弦较长
圆的切线垂直于过切点的半径;经过圆心且垂直于切线的直线必经过切点
经过切点且垂直于切线的直线必经过圆心
球心与截面圆(不是大圆)的圆心的连线垂直于截面圆
与球心距离相等的两截面圆相等;与球心距离不等的两截面圆不等,距球心较近的截面圆较大
球的切面垂直于过切点的半径;经过球心且垂直于切面的直线必经过切点
经过切点且垂直于切面的直线必经过球心
例3.(1)类比平面直角三角形的勾股定理, 试给出立体几何中类似的结论.
类比对象:
三角形
四面体
直角三角形
有三个面两两垂直的四面体
直角三角形
∠C=90°
3个边的长度a,b,c
2条直角边a,b和1条斜边c
3个面两两垂直的四面体
∠PDF=∠PDE=∠EDF=90°
4个面的面积S1,S2,S3和S
3个“直角面” S1,S2,S3和1个“斜面” S
例3.(2)在空间中与“等边三角形内任意一点P到三边的距离之和等于三角形的高”相类似的结论是什么?
类比对象:
正三角形
正四面体
正四面体内任一点到四个面的距离和等于正四面体的高.
类比推理的一般步骤:
(1)寻找合适的类比对象
(常已给出)
(2)找出两类对象之间可以确切表述的相似
特征;
(3)用一类对象的已知特征去推测另一类对
象的特征,从而得出一个猜想;
(4)检验猜想,即证明。
例4.已知: 等差数列{an}的公差为d , 前n项和为Sn , 有如下性质:
(1)an=am+(n-m)d
(2)若m+n=p+q , 其中m , n , p , q∈N*, 则am+an=ap+aq
(3)若m+n=2p , m , n , p∈N*, 则am+an=2ap
(4)Sn , S2n-Sn , S3n-S2n构成等差数列
类比上述性质, 在等比数列{bn}中, 写出相类似的性质.
等差数列 等比数列
定义
通项公式
前n项和
例1、利用等差数列性质类比等比数列性质
等差数列 等比数列
中项
性质
n+m=p+q时,
am+an= ap+aq
n+m=p+q时,
aman= apaq
任意实数a、b都有等差中项 ,为
当且仅当a、b同号时才有等比中项 ,为
成等差数列
成等比数列
下标等差,项等差
下标等差,项等比
课堂练习
1.作业7.平面中的三角形和空间四面体有着许多相类似的性质, 例如在三角形中:
(1)三角形两边之和大于第三边;
(2) S△= 底×高;
(3)三角形的中位线平行于第三边且等于第三
边的一半.
……那么在空间四面体中相应的结论是什么?
2.作业4.已知等差数列有一性质: 若 是等差数列,则通项 为的数列也是等差数列.类比上述命题,相应的等比数列有性质:若 是等比数列( ),则通项 = 的数列也是等比数列
练习1(2004广东,15)
由图(1)有面积关系:
则由图(2)有体积关系:
图(1)
图(2)
五、课堂小结:
1、运用类比方法解决问题,其基本过程可用框图
表示如下:
原问题
类比问题
原问题解法
类比问题的解法
2、运用类比法的关键是:寻找一个合适的类比对象。
几何中常见的类比对象
三角形
四面体(各面均为三角形)
四边形
六面体(各面均为四边形)
圆
球
代数中常见的类比对象
数
向量
方程
函数
不等式
交集,并集,补集
或,且,非运算
无限
有限
