5.7三角函数的应用-【新教材】人教A版(2019)高中数学必修第一册课件(共15张PPT)
文档属性
| 名称 | 5.7三角函数的应用-【新教材】人教A版(2019)高中数学必修第一册课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 425.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-17 20:06:11 | ||
图片预览





文档简介
5.5.7
新高考新教材
高中数第一册第五章三角函数
三 角 函 数 的 应 用
现实生活中存在大量具有周面复始,循环往复特点的周期运动变化现。如果某种变化着的现象具有周期性,那么就可以考虑借助三角函数来描述。本节通过几个具体实例说明三角函数模型的简单应用。
模型一:简谐运动
问题1:某个弹簧振子(简称振子)在完成一次全振动的过程 中,时间t(单位:秒)与位移(单位:mm)之间的对应数据如下表。试根据这些数据确定这个振子的位移关于时间的函数解析式
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}t
0.00
0.05
0.10
0.15
0.20
0.25
0.30
0.35
0.40
0.45
0.50
0.55
0.60
y
-20.0
-17.8
-10.1
0.1
10.3
17.7
20.0
17.7
10.3
0.1
-10.1
-17.8
-20.0
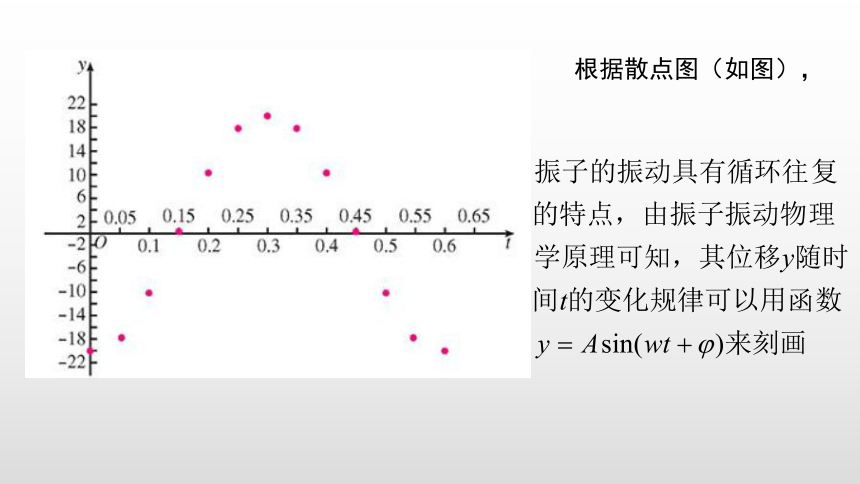
根据散点图(如图),
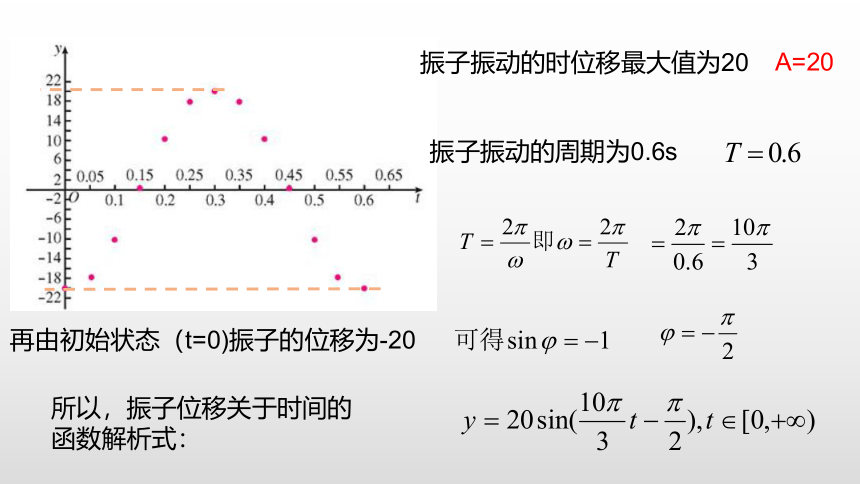
振子振动的时位移最大值为20
A=20
振子振动的周期为0.6s
再由初始状态(t=0)振子的位移为-20
所以,振子位移关于时间的函数解析式:
现实生活中存在大量类似弹簧振子的运动,如钟摆的摆动,水中浮标的上下浮动,琴弦的振动等。
物体都是物体在某一个中心位置附近循环往复的运动。在物理学中,把物体受到的力正比于离开平衡的距离的运动称为“简谐运动”
(1)
(2)
由交电流的道理原理可知,电流i随时间的变化规律可用 i=Asin(wt+φ)
电流最大值为5A,因此A=5
课本第244页练习第1题
感 谢 关 注
新高考新教材
高中数第一册第五章三角函数
三 角 函 数 的 应 用
现实生活中存在大量具有周面复始,循环往复特点的周期运动变化现。如果某种变化着的现象具有周期性,那么就可以考虑借助三角函数来描述。本节通过几个具体实例说明三角函数模型的简单应用。
模型一:简谐运动
问题1:某个弹簧振子(简称振子)在完成一次全振动的过程 中,时间t(单位:秒)与位移(单位:mm)之间的对应数据如下表。试根据这些数据确定这个振子的位移关于时间的函数解析式
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}t
0.00
0.05
0.10
0.15
0.20
0.25
0.30
0.35
0.40
0.45
0.50
0.55
0.60
y
-20.0
-17.8
-10.1
0.1
10.3
17.7
20.0
17.7
10.3
0.1
-10.1
-17.8
-20.0
根据散点图(如图),
振子振动的时位移最大值为20
A=20
振子振动的周期为0.6s
再由初始状态(t=0)振子的位移为-20
所以,振子位移关于时间的函数解析式:
现实生活中存在大量类似弹簧振子的运动,如钟摆的摆动,水中浮标的上下浮动,琴弦的振动等。
物体都是物体在某一个中心位置附近循环往复的运动。在物理学中,把物体受到的力正比于离开平衡的距离的运动称为“简谐运动”
(1)
(2)
由交电流的道理原理可知,电流i随时间的变化规律可用 i=Asin(wt+φ)
电流最大值为5A,因此A=5
课本第244页练习第1题
感 谢 关 注
