人教A版高中数学必修1第三章3.1.2 用二分法求方程的近似解课件(共22张PPT)
文档属性
| 名称 | 人教A版高中数学必修1第三章3.1.2 用二分法求方程的近似解课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-17 00:00:00 | ||
图片预览








文档简介
用二分法求方程的近似解
17:48:49
1
1、对于函数y=f(x),我们把使f(x)=0的 实数x 叫函数y=f(x)的零点
复习回顾
2、方程实根与对应函数零点之间的联系
方程f(x)=0实数根
函数y=f(x) 的图象与x轴交点
函数y=f(x)零点
17:48:49
2
3、如果函数y=f(x)在[a, b]上的图象是连续不断
的一条曲线,并且f(a)·f(b)<0,那么,函数y=f(x)
在区间(a, b)内有零点,即存在c∈(a, b),使得f( c )=0,
这个c 就是方程f(x)=0的根。
x
O
a
b
y
17:48:49
3
如何求出这个零点或零点的近似值呢?
通过上节课的学习我们知道:
函数f(x)=lnx+2x-6在区间(2,3)内有零点
17:48:49
4
知识探究(一):二分法的概念
思考1:从某水库闸房到防洪指挥部的某一处电话线路发生了故障。这是一条10km长的线路,如何迅速查出故障所在?
17:48:49
5
如图,设闸门和指挥部的所在处为点A,B,
B
A
C
6.这样每查一次,就可以把待查的线路长度缩减一半
1.首先从中点C查
2.用随身带的话机向两端测试时,发现AC段正常,断定
故障在BC段
3.再到BC段中点D
4.这次发现BD段正常,可见故障在CD段
5.再到CD中点E来看
D
E
17:48:49
6
1.解方程:x2+3x-1=0
提出问题:
2.关于方程:x3+3x-1=0
① 该方程有无实根?
②方程根的近似值约为多少?
分析:设f(x)=x3+3x-1 则 f(0)=-1<0,f(1)=3>0,
这说明函数f(x)在区间(0,1)内有零点。
x1≈0.3028,x2≈-3.3028
每次取中点,将区间一分为二,再经比较,按需要留下其中一个小区间的方法叫二分法,也叫对分法
17:48:49
7
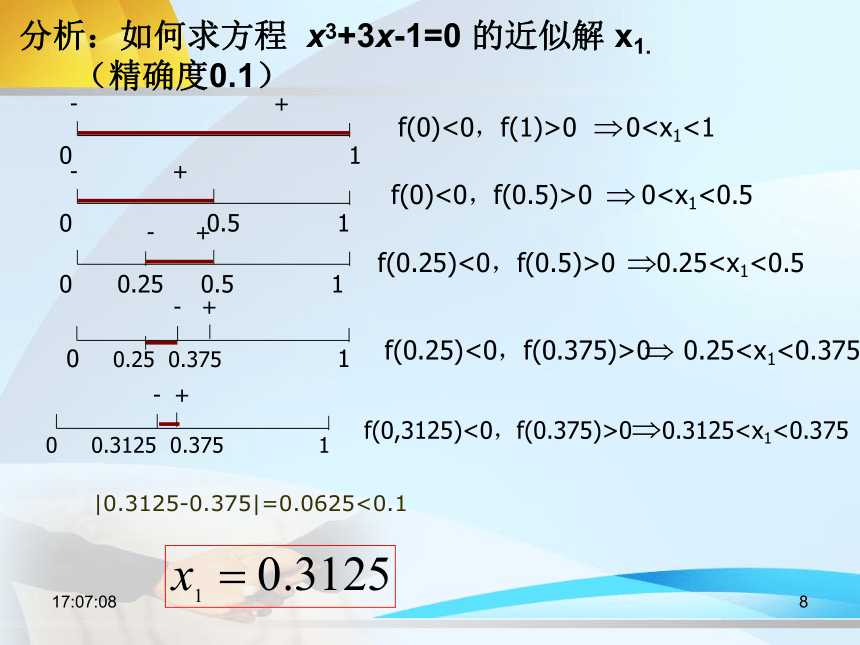
分析:如何求方程 x3+3x-1=0 的近似解 x1.
(精确度0.1)
- +
0 1
f(0)<0,f(1)>0 0- +
0 0.5 1
f(0)<0,f(0.5)>0 0- +
0 0.25 0.5 1
f(0.25)<0,f(0.5)>0 0.25- +
0 0.25 0.375 1
f(0.25)<0,f(0.375)>0 0.25- +
0 0.3125 0.375 1
f(0,3125)<0,f(0.375)>0 0.3125|0.3125-0.375|=0.0625<0.1
17:48:49
8
上述求函数零点近似值的方法叫做二分法,那么二分法的基本思想是什么?
对于在区间[a,b]上连续不断且f(a)·f(b)<0的函数y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法.
x
y
0
a
b
17:48:49
9
对于在①区间[a,b]上连续不断且f(a) ·f(b)<0的函数 y=f(x) ,通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逼近零点,进而得到零点近似值。
根基
x
y
0
a
b
二分法
思想方法:
17:48:49
10
练习1:
下列函数的图象与x轴均有交点,其中不能用二分法求其零点的是 ( )
C
x
y
0
x
y
0
x
y
0
x
y
0
17:48:49
11
对于在①区间[a,b]上连续不断且f(a) ·f(b)<0的函数 y=f(x) ,通过②不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逼近零点,进而得到零点近似值。
根基
主干
x
y
0
a
b
二分法
思想方法:
17:48:49
12
对于在①区间[a,b]上连续不断且f(a) ·f(b)<0的函数 y=f(x) ,通过②不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逼近零点,进而③得到零点近似值。
根基
主干
终端
x
y
0
a
b
二分法
思想方法:
17:48:49
13
思考1:求函数f(x)的零点近似值第一步应做什么?
知识探究(二):
用二分法求函数零点近似值的步骤
思考2:为了缩小零点所在区间的范围,接下来应做什么?
确定区间[a,b],使 f(a)f(b)<0
求区间的中点c,并计算f(c)的值
17:48:49
14
思考3:若f(c)=0说明什么? 若f(a)·f(c)<0或f(c)·f(b)<0 ,则分别说明什么?
若f(c)=0 ,则c就是函数的零点;
若f(a)·f(c)<0 ,则零点x0∈(a,c);
若f(c)·f(b)<0 ,则零点x0∈(c,b).
思考4:若给定精确度ε,如何选取近似值?
当|a—b|<ε时,区间[a,b]内的任意一个值都是函数零点的近似值.一般我们取区间的端点a(或b)
17:48:49
15
用二分法求函数零点近似值的基本步骤:
3. 计算f(c):
(1)若f(c)=0,则c就是函数的零点;
(2)若f(a)·f(c)<0 ,则令b=c,此时零点 x0∈(a,c);
(3)若f(c)·f(b)<0 ,则令a=c,此时零点 x0∈(c,b).
2. 求区间(a,b)的中点c;
1.确定区间[a,b],使f(a)·f(b)<0 ,给定精度ε;
17:48:49
16
4. 判断是否达到精确度ε:若 ,则得到零点近似值a(或b),否则重复步骤2~4.
记忆口诀:定区间,找中点,中值计算两边看.
同号去,异号算,零点落在异号间.
周而复始怎么办? 精确度上来判断.
17:48:49
17
例题分析
例1.用二分法求函数f(x)=lnx+2x-6在区间(2,3)
内的零点的近似解(精确度0.1)
请看下面的表格:
17:48:49
18
区间
端点的符号
中点的值
中点函数值 的符号
(2,3)
f(2)<0, f(3)>0
2.5
f(2.5)<0
(2.5,3)
f(2.5)<0,f(3)>0
2.75
f(2.75)>0
(2.5,2.75)
f(2.5)<0,
f(2.75)>0
2.625
f(2.625)>0
(2.5,2.625)
f(2.5)<0, f(2.625)>0
2.5625
f(2.5625)>0
(2.5,2.5625)
由于 ?2.5-2.5625?=0.0625<0.1
所以,原函数的零点近似解为2.5625
17:48:49
19
借助计算器或计算机用二分法求方程 +3x
=7的近似解(精确到0.1)
快快动手吧!
17:48:49
20
小结和作业
1.二分法的定义;
2.用二分法求函数零点近似值的步骤。
3.作业:p92 第3、5题
记忆口诀:定区间,找中点,中值计算两边看.
同号去,异号算,零点落在异号间.
周而复始怎么办? 精确度上来判断.
17:48:49
21
谢谢大家
17:48:49
22
17:48:49
1
1、对于函数y=f(x),我们把使f(x)=0的 实数x 叫函数y=f(x)的零点
复习回顾
2、方程实根与对应函数零点之间的联系
方程f(x)=0实数根
函数y=f(x) 的图象与x轴交点
函数y=f(x)零点
17:48:49
2
3、如果函数y=f(x)在[a, b]上的图象是连续不断
的一条曲线,并且f(a)·f(b)<0,那么,函数y=f(x)
在区间(a, b)内有零点,即存在c∈(a, b),使得f( c )=0,
这个c 就是方程f(x)=0的根。
x
O
a
b
y
17:48:49
3
如何求出这个零点或零点的近似值呢?
通过上节课的学习我们知道:
函数f(x)=lnx+2x-6在区间(2,3)内有零点
17:48:49
4
知识探究(一):二分法的概念
思考1:从某水库闸房到防洪指挥部的某一处电话线路发生了故障。这是一条10km长的线路,如何迅速查出故障所在?
17:48:49
5
如图,设闸门和指挥部的所在处为点A,B,
B
A
C
6.这样每查一次,就可以把待查的线路长度缩减一半
1.首先从中点C查
2.用随身带的话机向两端测试时,发现AC段正常,断定
故障在BC段
3.再到BC段中点D
4.这次发现BD段正常,可见故障在CD段
5.再到CD中点E来看
D
E
17:48:49
6
1.解方程:x2+3x-1=0
提出问题:
2.关于方程:x3+3x-1=0
① 该方程有无实根?
②方程根的近似值约为多少?
分析:设f(x)=x3+3x-1 则 f(0)=-1<0,f(1)=3>0,
这说明函数f(x)在区间(0,1)内有零点。
x1≈0.3028,x2≈-3.3028
每次取中点,将区间一分为二,再经比较,按需要留下其中一个小区间的方法叫二分法,也叫对分法
17:48:49
7
分析:如何求方程 x3+3x-1=0 的近似解 x1.
(精确度0.1)
- +
0 1
f(0)<0,f(1)>0 0
0 0.5 1
f(0)<0,f(0.5)>0 0
0 0.25 0.5 1
f(0.25)<0,f(0.5)>0 0.25
0 0.25 0.375 1
f(0.25)<0,f(0.375)>0 0.25
0 0.3125 0.375 1
f(0,3125)<0,f(0.375)>0 0.3125
17:48:49
8
上述求函数零点近似值的方法叫做二分法,那么二分法的基本思想是什么?
对于在区间[a,b]上连续不断且f(a)·f(b)<0的函数y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法.
x
y
0
a
b
17:48:49
9
对于在①区间[a,b]上连续不断且f(a) ·f(b)<0的函数 y=f(x) ,通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逼近零点,进而得到零点近似值。
根基
x
y
0
a
b
二分法
思想方法:
17:48:49
10
练习1:
下列函数的图象与x轴均有交点,其中不能用二分法求其零点的是 ( )
C
x
y
0
x
y
0
x
y
0
x
y
0
17:48:49
11
对于在①区间[a,b]上连续不断且f(a) ·f(b)<0的函数 y=f(x) ,通过②不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逼近零点,进而得到零点近似值。
根基
主干
x
y
0
a
b
二分法
思想方法:
17:48:49
12
对于在①区间[a,b]上连续不断且f(a) ·f(b)<0的函数 y=f(x) ,通过②不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逼近零点,进而③得到零点近似值。
根基
主干
终端
x
y
0
a
b
二分法
思想方法:
17:48:49
13
思考1:求函数f(x)的零点近似值第一步应做什么?
知识探究(二):
用二分法求函数零点近似值的步骤
思考2:为了缩小零点所在区间的范围,接下来应做什么?
确定区间[a,b],使 f(a)f(b)<0
求区间的中点c,并计算f(c)的值
17:48:49
14
思考3:若f(c)=0说明什么? 若f(a)·f(c)<0或f(c)·f(b)<0 ,则分别说明什么?
若f(c)=0 ,则c就是函数的零点;
若f(a)·f(c)<0 ,则零点x0∈(a,c);
若f(c)·f(b)<0 ,则零点x0∈(c,b).
思考4:若给定精确度ε,如何选取近似值?
当|a—b|<ε时,区间[a,b]内的任意一个值都是函数零点的近似值.一般我们取区间的端点a(或b)
17:48:49
15
用二分法求函数零点近似值的基本步骤:
3. 计算f(c):
(1)若f(c)=0,则c就是函数的零点;
(2)若f(a)·f(c)<0 ,则令b=c,此时零点 x0∈(a,c);
(3)若f(c)·f(b)<0 ,则令a=c,此时零点 x0∈(c,b).
2. 求区间(a,b)的中点c;
1.确定区间[a,b],使f(a)·f(b)<0 ,给定精度ε;
17:48:49
16
4. 判断是否达到精确度ε:若 ,则得到零点近似值a(或b),否则重复步骤2~4.
记忆口诀:定区间,找中点,中值计算两边看.
同号去,异号算,零点落在异号间.
周而复始怎么办? 精确度上来判断.
17:48:49
17
例题分析
例1.用二分法求函数f(x)=lnx+2x-6在区间(2,3)
内的零点的近似解(精确度0.1)
请看下面的表格:
17:48:49
18
区间
端点的符号
中点的值
中点函数值 的符号
(2,3)
f(2)<0, f(3)>0
2.5
f(2.5)<0
(2.5,3)
f(2.5)<0,f(3)>0
2.75
f(2.75)>0
(2.5,2.75)
f(2.5)<0,
f(2.75)>0
2.625
f(2.625)>0
(2.5,2.625)
f(2.5)<0, f(2.625)>0
2.5625
f(2.5625)>0
(2.5,2.5625)
由于 ?2.5-2.5625?=0.0625<0.1
所以,原函数的零点近似解为2.5625
17:48:49
19
借助计算器或计算机用二分法求方程 +3x
=7的近似解(精确到0.1)
快快动手吧!
17:48:49
20
小结和作业
1.二分法的定义;
2.用二分法求函数零点近似值的步骤。
3.作业:p92 第3、5题
记忆口诀:定区间,找中点,中值计算两边看.
同号去,异号算,零点落在异号间.
周而复始怎么办? 精确度上来判断.
17:48:49
21
谢谢大家
17:48:49
22
