变化率与导数
图片预览








文档简介
(共25张PPT)
1.1 变化率与导数
一.创设情景
为了描述现实世界中运动、过程等变化着的现象,在数学中引入了函数,随着对函数的研究,产生了微积分,微积分的创立以自然科学中四类问题的处理直接相关:
一、已知物体运动的路程作为时间的函数,求物体在任意时刻的速度与加速度等;
二、求曲线的切线;
三、求已知函数的最大值与最小值;
四、求长度、面积、体积和重心等。
导数是微积分的核心概念之一它是研究函数增减、变化快慢、最大(小)值等问题最一般、最有效的工具。
导数研究的问题即变化率问题:研究某个变量相对于另一个变量变化的快慢程度.
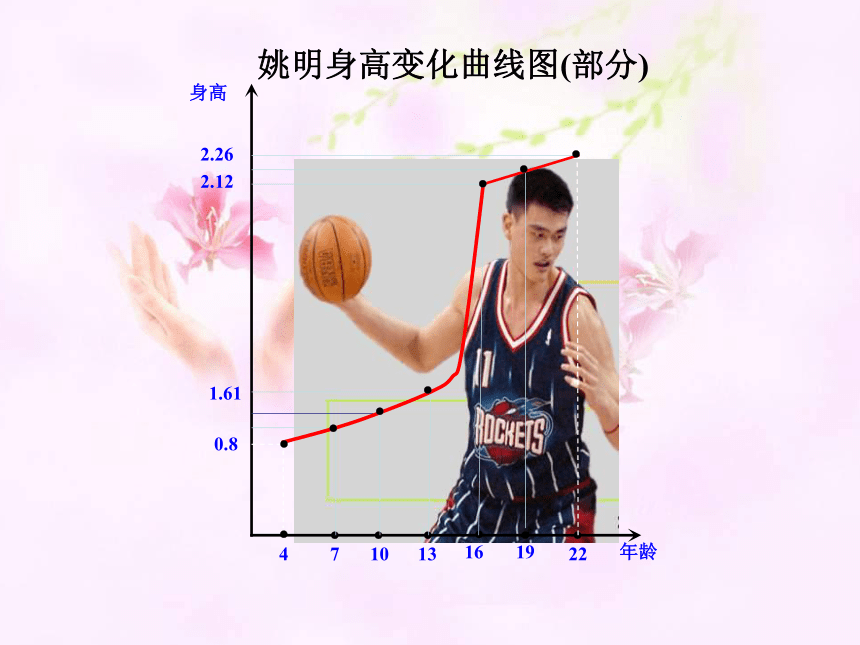
姚明身高变化曲线图(部分)
2.26
2.12
●
●
●
●
●
●
年龄
身高
4
7
10
13
16
●
19
22
0.8
1.61
●
●
●
●
●
●
●
在吹气球的过程中, 可发现,随着气球内空气容量的增加, 气球的半径增加得越来越慢. 从数学的角度, 如何描述这种现象呢
探究过程:如图是函数h(t)= -4.9t2+6.5t+10的图像,结合图形可知, ,
所以,
虽然运动员在 这段时间里的平均速度为 ,但实际情况是运动员仍然运动,并非静止,可以说明用平均速度不能精确描述运动员的运动状态.
t
h
O
直线AB的斜率
A
B
例 (1) 计算函数 f (x) = 2 x +1在区间[ –3 , –1]上的平均变化率 ;
(2) 求函数f (x) = x2 +1的平均变化率。
(1)解:
△y=f (-1)- f (-3)=4
△x=-1- (-3)=2
(2)解:
△y=f (x+△x)- f (x)
=2△x ·x+(△x )2
练习
A
小结:
1.函数的平均变化率
2.求函数的平均变化率的步骤:
(1)求函数的增量:Δy=f(x2)-f(x1);
(2)计算平均变化率:
任意取一个时刻2+ , 是时间改变量,可以是正值,也可以为负值,但是不为0
无论t从小于2的一边,还是从大于2的一边趋近于2时,平均速度趋近于一个确定的值-13.1
从物理学的角度看,时间间隔 无限变小时,平均速度 就无限趋近于t=2时的瞬时速度,因此,运动员在t=2时的瞬时速度是-13.1m/s
含义:当t=2时, 趋近于0时,平均速
度 趋近于确定值-13.1
运动员在某一时刻 的瞬时速度怎样表示?
函数 在 处的瞬时变化率怎样表示?
函数y=f(x)在 处的瞬时变化率是
我们称它为函数y=f(x)在 处的导数,记做
即
例1
练习
6
3
6
27
对于上面的导数有什么实际意义?
在第2h附近,原有大约以3 的速率下降,在第6h附近,原有温度大约以5 的速率上升
1.1 变化率与导数
一.创设情景
为了描述现实世界中运动、过程等变化着的现象,在数学中引入了函数,随着对函数的研究,产生了微积分,微积分的创立以自然科学中四类问题的处理直接相关:
一、已知物体运动的路程作为时间的函数,求物体在任意时刻的速度与加速度等;
二、求曲线的切线;
三、求已知函数的最大值与最小值;
四、求长度、面积、体积和重心等。
导数是微积分的核心概念之一它是研究函数增减、变化快慢、最大(小)值等问题最一般、最有效的工具。
导数研究的问题即变化率问题:研究某个变量相对于另一个变量变化的快慢程度.
姚明身高变化曲线图(部分)
2.26
2.12
●
●
●
●
●
●
年龄
身高
4
7
10
13
16
●
19
22
0.8
1.61
●
●
●
●
●
●
●
在吹气球的过程中, 可发现,随着气球内空气容量的增加, 气球的半径增加得越来越慢. 从数学的角度, 如何描述这种现象呢
探究过程:如图是函数h(t)= -4.9t2+6.5t+10的图像,结合图形可知, ,
所以,
虽然运动员在 这段时间里的平均速度为 ,但实际情况是运动员仍然运动,并非静止,可以说明用平均速度不能精确描述运动员的运动状态.
t
h
O
直线AB的斜率
A
B
例 (1) 计算函数 f (x) = 2 x +1在区间[ –3 , –1]上的平均变化率 ;
(2) 求函数f (x) = x2 +1的平均变化率。
(1)解:
△y=f (-1)- f (-3)=4
△x=-1- (-3)=2
(2)解:
△y=f (x+△x)- f (x)
=2△x ·x+(△x )2
练习
A
小结:
1.函数的平均变化率
2.求函数的平均变化率的步骤:
(1)求函数的增量:Δy=f(x2)-f(x1);
(2)计算平均变化率:
任意取一个时刻2+ , 是时间改变量,可以是正值,也可以为负值,但是不为0
无论t从小于2的一边,还是从大于2的一边趋近于2时,平均速度趋近于一个确定的值-13.1
从物理学的角度看,时间间隔 无限变小时,平均速度 就无限趋近于t=2时的瞬时速度,因此,运动员在t=2时的瞬时速度是-13.1m/s
含义:当t=2时, 趋近于0时,平均速
度 趋近于确定值-13.1
运动员在某一时刻 的瞬时速度怎样表示?
函数 在 处的瞬时变化率怎样表示?
函数y=f(x)在 处的瞬时变化率是
我们称它为函数y=f(x)在 处的导数,记做
即
例1
练习
6
3
6
27
对于上面的导数有什么实际意义?
在第2h附近,原有大约以3 的速率下降,在第6h附近,原有温度大约以5 的速率上升
