黑龙江省大庆市肇源县(五四学制)2020-2021学年八年级上学期期末数学试题(Word版 含解析)
文档属性
| 名称 | 黑龙江省大庆市肇源县(五四学制)2020-2021学年八年级上学期期末数学试题(Word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 531.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-15 14:41:40 | ||
图片预览



文档简介
2020-2021学年八年级上学期期末数学试题
一、单选题
1.若,则下列式子错误的是( ).
A. B. C. D.
2.等腰三角形是轴对称图形,它的对称轴是( )
A.中线 B.底边上的中线 C.中线所在的直线 D.底边上的中线所在的直线
3.如图,在中,的垂直平分线交于点,平分,若,则的度数为( )
A. B. C. D.
4.若关于x的方程有增根,则k的值为( ).
A.3 B.1 C.0 D.-1
5.若,则的大小关系是 ( )
A. B. C. D.
6.某商品的进价是500元,标价是750元,商店要求以利润率为5%的售价打折出售,售货员可以打几折出售此商品( )
A.5 B.6 C.7 D.8
7.如图,中,,将绕点A按顺时针方向旋转,得到,则的度数为( )
A. B. C. D.
8.甲、乙两地之间的高速公路全长200千米,比原来国道的长度减少了20千米.高速公路通车后,某长途汽车的行驶速度提高了45千米/时,从甲地到乙地的行驶时间缩短了一半.设该长途汽车在原来国道上行驶的速度为x千米/时,根据题意,下列方程正确的是( )
A. B.
C. D.
9.一个正多边形的内角和等于1080°,这个正多边形的每个外角是( )
A.30° B.45° C.60° D.75°
10.关于的不等式组,有四个整数解,则的取值范围是( )
A. B. C. D.
二、填空题
11.如图,点P是∠AOB平分线OC上一点,PD⊥OB,垂足为D,若PD=2,则点P到边OA的距离是_____.
12.一个正多边形的内角和是外角和的3倍,则这个正多边形的一个内角的度数是______度.
13.某校组织开展了“诗词大会”的知识竞赛初赛,共有 20 道题. 答对一题加 10 分,答错 或不答一题扣 5 分,小辉在初赛得分超过 160 分顺利进入决赛. 设他答对 x 道题,根据题意,可列出关于 x 的不等式为 __________.
14.若分式的值为0,则x的值为_______.
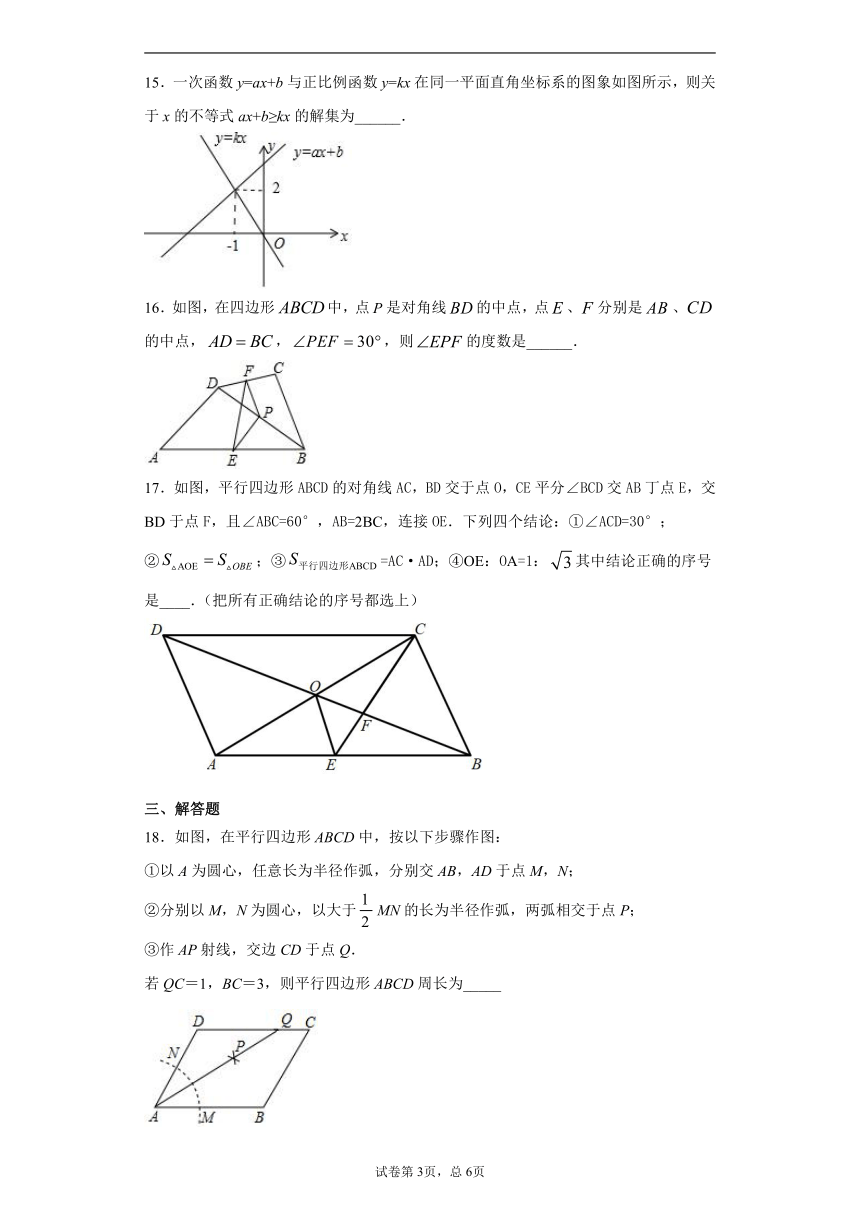
15.一次函数y=ax+b与正比例函数y=kx在同一平面直角坐标系的图象如图所示,则关于x的不等式ax+b≥kx的解集为______.
16.如图,在四边形中,点是对角线的中点,点、分别是、的中点,,,则的度数是______.
17.如图,平行四边形ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB丁点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列四个结论:①∠ACD=30°;②;③=AC·AD;④OE:OA=1:其中结论正确的序号是____.(把所有正确结论的序号都选上)
三、解答题
18.如图,在平行四边形ABCD中,按以下步骤作图:
①以A为圆心,任意长为半径作弧,分别交AB,AD于点M,N;
②分别以M,N为圆心,以大于MN的长为半径作弧,两弧相交于点P;
③作AP射线,交边CD于点Q.
若QC=1,BC=3,则平行四边形ABCD周长为_____
19.解方程:? ? ? ? ? ? ? ??
20.化简并求值:(1-)÷,其中x=-1
21.因式分解:
(1);
(2).
22.如图,在?ABCD中,点E,F在AC上,且∠ABE=∠CDF,求证:BE=DF.
23.在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣4,5),C(﹣5,2).
(1)画出△ABC关于原点O成中心对称的△A1B1C1;
(2)写出△A1B1C1的顶点坐标;
(3)求出△A1B1C1的面积.
24.如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10,将△APB绕点B逆时针旋转一定角度后,可得到△CQB.
(1)求点P与点Q之间的距离;?
(2)求∠APB的度数.
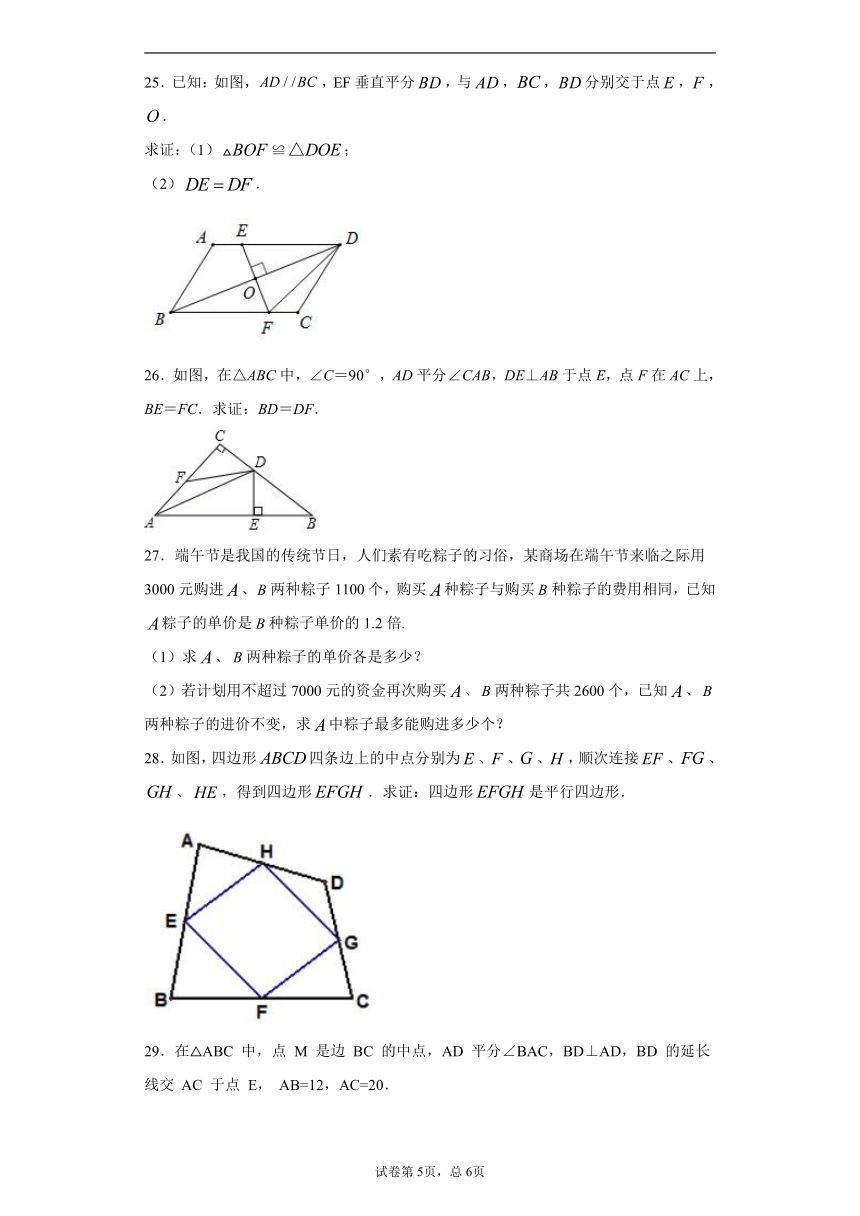
25.已知:如图,,EF垂直平分,与,,分别交于点,,.
求证:(1)≌;
(2).
26.如图,在△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,点F在AC上,BE=FC.求证:BD=DF.
27.端午节是我国的传统节日,人们素有吃粽子的习俗,某商场在端午节来临之际用3000元购进、两种粽子1100个,购买种粽子与购买种粽子的费用相同,已知粽子的单价是种粽子单价的1.2倍.
(1)求、两种粽子的单价各是多少?
(2)若计划用不超过7000元的资金再次购买、两种粽子共2600个,已知、两种粽子的进价不变,求中粽子最多能购进多少个?
28.如图,四边形四条边上的中点分别为、、、,顺次连接、、、,得到四边形.求证:四边形是平行四边形.
29.在△ABC 中,点 M 是边 BC 的中点,AD 平分∠BAC,BD⊥AD,BD 的延长线交 AC 于点 E, AB=12,AC=20.
(1)求证:BD=DE;
(2)求 DM 的长.
参考答案
1.D
【分析】
利用不等式的性质判断即可得到结果.
【详解】
解:若x>y,
则有x-3>y-3; ;-2x<-2y; 3-x<3-y
故选D.
【点睛】
本题考查不等式的性质,熟练掌握不等式的性质是解本题的关键.
2.D
【分析】
根据等腰三角形的三线合一的性质,可得出答案.
【详解】
解:等腰三角形的对称轴是顶角的角平分线所在直线,底边高所在的直线,底边中线所在直线,
A、中线,错误;
B、底边上的中线,错误;
C、中线所在的直线,错误;
D、底边上的中线所在的直线,正确.
故选D.
【点睛】
本题考查了轴对称图形的知识,解答本题的关键是掌握轴对称及对称轴的定义.
3.B
【分析】
根据垂直平分线的性质和角平分线的定义求得∠ACB的度数,再根据三角形内角和求出∠B的度数.
【详解】
解:∵DE是AC的垂直平分线,
∴AD=CD,∠ACD=∠A=50°,
∵平分,
∴∠ACB=2∠ACD=100°,
∴∠B=180°-100°-50°=30°,
故选:B.
【点睛】
本题考查垂直平分线的性质、角平分线的定义和三角形内角和定理,熟练掌握垂直平分线的性质和角平分线的定义是解题的关键.
4.A
【解析】
试题解析:首先根据解分式方程的方法求出x的值,然后根据增根为x=1代入方程求出k的值.将方程的两边同时乘以(x-1)可得:3=x-1+k,解得:x=4-k,根据方程有增根可得:x=1,即4-k=1,k=3.
5.B
【分析】
根据时,可得越平方越小,,从而得到大小关系式.
【详解】
,
,,
,
故选:B.
【点睛】
本题考查了简单的实数的比较,可利用特殊值法即可比较大小,也可利用当时,的指数越大则数值越小解题.
6.C
【分析】
设售货员可以打x折出售此商品,根据:标价×-进价=进价×5%即可得出关于x的一元一次方程,解之即可得出结论.
【详解】
设售货员可以打x折出售此商品,
根据题意得:750×﹣500=500×5%,
解得:x=7,即售货员可以打7折出售此商品.
故选C.
【点睛】
本题考查了一元一次方程的应用,知道:商品的实际售价=商品标价×,找准等量关系,正确列出一元一次方程是解题的关键.
7.A
【分析】
根据∠BAC′=∠CAC′-∠CAB计算即可解决问题.
【详解】
∵∠CAC′=70°,∠CAB=36°,
∴∠BAC′=∠CAC′-∠CAB=70°-36°=34°,
故选:A.
【点睛】
本题考查了旋转变换,角的和差定义等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
8.B
【解析】
试题分析:设该长途汽车在原来国道上行驶的速度为x千米/时,根据题意得
.
故选B.
考点:由实际问题抽象出分式方程.
9.B
【分析】
首先设此多边形为n边形,根据题意得:180(n-2)=1080,即可求得n=8,再由多边形的外角和等于360°,即可求得答案.
【详解】
解:设此多边形为n边形,
根据题意得:180(n-2)=1080,
解得:n=8,
∴这个正多边形的每一个外角等于:360°÷8=45°.
故选:B.
【点睛】
此题考查了多边形的内角和与外角和的知识.注意掌握多边形内角和定理:(n-2)?180°,外角和等于360°.
10.A
【分析】
先求出不等式组中每个不等式的解集,然后求出其公共解集,最后求其整数解进而求a的取值范围.
【详解】
解:解不等式3x>2x+1,
得:x>1,
解不等式2-x>a,
得:x<2-a,
则不等式组的解集为1∵不等式组的整数解有4个,即2、3、4,5,
∴5<2-a≤6,
解得:,
故选:A.
【点睛】
本题考查不等式组的解法及整数解的确定,求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了,掌握知识点是解题关键.
11.2
【分析】
作PE⊥OA,再根据角平分线的性质得出PE=PD即可得出答案.
【详解】
过P作PE⊥OA于点E,
∵点P是∠AOB平分线OC上一点,PD⊥OB,
∴PE=PD,
∵PD=2,
∴PE=2,
∴点P到边OA的距离是2.
故答案为2.
【点睛】
本题考查角平分线的性质,关键在于牢记角平分线的性质并灵活运用.
12.135
【分析】
先由多边形的内角和和外角和的关系判断出多边形的边数,即可得到结论.
【详解】
设多边形的边数为n.
因为正多边形内角和为(n?2)?180°,正多边形外角和为360°,
根据题意得:(n?2)?180°=360°×3,
解得:n=8.
∴这个正多边形的每个外角==45°,
则这个正多边形的每个内角是180°?45°=135°,
故答案为:135.
【点睛】
本题考查了正多边形的内角与外角,正多边形的性质;熟练掌握正多边形的性质,求出正多边形的边数是解决问题的关键.
13.
【分析】
竞赛得分=10×答对的题数-5×未答对的题数,根据本次竞赛得分要超过160分,列出不等式即可.
【详解】
解:设答对x道题,则答错(20-x)道,根据题意可得
.
故答案为.
点睛:本题考查了一元一次不等式在实际问题的应用,解决此类问题的关键是在理解题意的基础上,建立与之相应的解决问题的“数学模型”——不等式,再由不等式的相关知识确定问题的答案.
14.-3
【分析】
根据分式的值为零的条件可以求出x的值.
【详解】
解:根据题意得:,
解得:x=-3.
故答案为:-3.
【点睛】
若分式的值为零,需同时具备两个条件:(1)分子为0;(2)分母不为0.这两个条件缺一不可.
15.x≥﹣1
【分析】
由图象可以知道,当x=-1时,两个函数的函数值是相等的,再根据函数的增减性可以判断出不等式ax+b≥kx解集.
【详解】
两个条直线的交点坐标为(?1, 2),且当x≥?1时,直线y=kx在y=ax+b直线的下方,故不等式ax+b≥kx的解集为x≥?1.
故答案为x≥?1.
【点睛】
本题考查了一次函数与一元一次不等式的知识点,解题的关键是根据图象可知一次函数与一元一次不等式的增减性.
16.
【分析】
根据中位线定理推出PE=AD,PF=BC,由此得到PE=PF,推出△PEF是等腰三角形,根据三角形的内角和定理求出答案.
【详解】
∵点是对角线的中点,点、分别是、的中点,
∴PE=AD,PF=BC,
∵,
∴PE=PF,
∴△PEF是等腰三角形,
∴∠PFE=,
∴=,
故答案为:.
【点睛】
此题考查三角形的中位线定义及定理,等腰三角形的判定及性质,三角形的内角和定理,熟记三角形的中位线的定义及定理是解题的关键.
17.①②③④
【分析】
由四边形ABCD是平行四边形,得到∠ABC=∠ADC=60°,∠BAD=120°,根据角平分线的定义得到∠DCE=∠BCE=60°推出△CBE是等边三角形,证得∠ACB=90°,求出∠ACD=∠CAB=30°,故①正确;由AC⊥BC,得到S?ABCD=AC?BC,故③正确,根据直角三角形的性质得到AC=BC,根据三角形的中位线的性质得到OE=BC,AE=BE,于是得到②④正确.
【详解】
∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC=60°,∠BAD=120°,
∵CE平分∠BCD交AB于点E,
∴∠DCE=∠BCE=60°
∴△CBE是等边三角形,
∴BE=BC=CE,
∵AB=2BC,
∴AE=BC=CE,
∴∠ACB=90°,
∴∠ACD=∠CAB=30°,故①正确;
∵AC⊥BC,
∴=AC·AD,故③正确,
在Rt△ACB中,∠ACB=90°,∠CAB=30°,
∴AC=BC,
∵AO=OC,AE=BE,
∴OE=BC,OA=BC,
∴OE:OA==,
故④正确;
∵AE=BE,∴S△AOE=S△OBE,故②正确;
答案为:①②③④
【点睛】
此题考查了平行四边形的性质、三角形中位线的性质以及等边三角形的判定与性质.注意证得△BCE是等边三角形,OE是△ABC的中位线是关键.
18.14
【分析】
根据角平分线的性质可知∠DAQ=∠BAQ,再由平行四边形的性质得出CD∥AB,BC=AD=3,∠BAQ=∠DQA,故可得出△AQD是等腰三角形,据此可得出DQ=AD,进而可得出平行四边形ABCD周长.
【详解】
解:如图:
∵由作图可知,AQ是∠DAB的平分线,
∴∠DAQ=∠BAQ.
∵四边形ABCD是平行四边形,
∴CD∥AB,BC=AD=3,∠BAQ=∠DQA,
∴∠DAQ=∠DQA,
∴△AQD是等腰三角形,
∴DQ=AD=3.
∵QC=1,
∴CD=DQ+CQ=3+1=4,
∴平行四边形ABCD周长=2(DC+AD)=2×(4+3)=14.
故答案为:14.
【点睛】
本题考查的是复杂作图,解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.
19.;
【分析】
根据解分式方程的一般步骤解方程即可求解.
【详解】
解:?
方程两边同乘以(x-2)得 ,
,
,
,
检验:当时,,
所以是原分式方程的解;
解:方程两边同时乘以x(x-2)得 ,
解得 ,
检验:当时,x(x-2)≠0,
所以,原分式方程的解为.
【点睛】
本题考查了分式方程的解法,解分式方程的一般步骤是去分母化为整式方程,解整式方程,检验三步骤.
20.原式=
【分析】
原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把x的值代入计算即可求出值.
【详解】
解:
当时,原式
【点睛】
此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.
21.(1);(2)
【分析】
(1)利用平方差公式分解因式即可;
(2)直接提取公因式2y,再利用完全平方公式分解因式即可.
【详解】
(1);
(2).
【点睛】
本题考查提取公因式法以及公式法分解因式,正确应用公式是解题关键.
22.证明见解析.
【分析】
利用ASA即可得证;
【详解】
∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∵AB∥CD,∴∠BAE=∠DCF
∴在△ABE和△CDF中,,∴△ABE≌△CDF,∴BE=DF.
考点:1.平行四边形的性质;2.三角形全等的判定与性质.
23.(1)答案见解析;(2)点A1(2,﹣1)、B1(4,﹣5)、C1(5,﹣2);(3)5.
【解析】
试题分析:(1)分别作出点A、B、C关于原点O的对称点,再顺次连接即可;
(2)根据所作图形得出答案即可;
(3)利用割补法求解即可.
试题解析:解:(1)如图所示,△A1B1C1即为所求;
(2)点A1(2,﹣1)、B1(4,﹣5)、C1(5,﹣2);
(3)=3×4﹣×1×3﹣×2×4﹣×1×3=5.
点睛:本题主要考查作图-旋转变换,解题的关键是根据旋转的性质作出变换后的对应点及割补法求三角形的面积.
24.(1)6;(2)150°
【解析】
试题分析:先根据等边三角形的性质得AB=AC,∠BAC=60°,再利用旋转的性质得∠P′AP=∠BAC=60°,AP′=AP,BP′=CP=13,于是可判断△AP′P为等边三角形,得到PP′=AP=5,∠APP′=60°,接着根据勾股定理的逆定理证明△BPP′为直角三角形,且∠BPP′=90°,然后利用∠APB=∠APP′+∠BPP′求出∠APB的度数.
试题解析:∵△ABC为等边三角形,∴AB=AC,∠BAC=60°,
∵△PAC绕点A逆时针旋转后,得到△P′AB,
∴∠P′AP=∠BAC=60°,AP′=AP,BP′=CP=13,
∴△AP′P为等边三角形,
∴PP′=AP=5,∠APP′=60°,
在△BPP′中,∵PP′=5,BP=12,BP′=13,
∴PP′2+BP2=BP′2,
∴△BPP′为直角三角形,∠BPP′=90°,
∴∠APB=∠APP′+∠BPP′=60°+90°=150°.
答:点P与点P′之间的距离为5,∠APB的度数为150°.
【考点】旋转的性质;勾股定理的逆定理.
25.(1)见解析;(2)见解析
【分析】
(1)利用AAS判定即可;
(2)根据△BOF≌△DOE得到OE=OF,由,推出BD是EF的垂直平分线,由此得到结论.
【详解】
证明:(1),
,
垂直平分BD,
,,
在和中
≌;
(2)由(1)可知≌,
,且,
为线段EF的垂直平分线,
.
【点睛】
此题考查全等三角形的判定及性质,线段垂直平分线的判定及性质,熟记定理是解题的关键.
26.详见解析.
【分析】
因为∠C=90°,DE⊥AB,所以∠C=∠DEB,根据角平分线的性质得到CD=DE,根据SAS判定△DCF≌△DEB,根据全等三角形的性质即可得到结论.
【详解】
∵AD平分∠BAC,DE⊥AB,∠C=90°,
∴DC=DE.
在△DCF和△DEB中,
∵,
∴△DCF≌△DEB(SAS),
∴BD=DF.
【点睛】
本题考查了角平分线的性质,全等三角形的判定和性质,熟练掌握全等三角形的判定和性质定理是解题的关键.
27.(l)种粽子的单价是3元,种粽子的单价是2.5元;(2)种粽子最多能购进1000个.
【分析】
(1)根据题意列出分式方程计算即可,注意根的验证.
(2)根据题意列出不等式即可,根据不等式的性质求解.
【详解】
(l)设种粽子的单价为元,则种粽子的单价为元
根据题意,得
解得:
经检验,是原方程的根
所以种粽子的单价是3元,种粽子的单价是2.5元
(2)设种粽子购进个,则购进种粽子个
根据题意,得
解得
所以,种粽子最多能购进1000个
【点睛】
本题主要考查分式方程的应用,关键在于分式方程的解需要验证.
28.见解析
【分析】
连接AC,根据三角形的中位线定理得到,,同理推出,,根据一组对边平行且相等的四边形是平行四边形得出四边形EFGH是平行四边形
【详解】
证明:连接AC.
是DC的中点,H是AD的中点,
,且,
同理可知,且,
,且,
四边形是平行四边形.
【点睛】
本题主要考查对三角形的中位线定理,平行四边形的判定,解题的关键是正确的构造三角形病正确的运用中位线定理,难度不大.
29.(1)见解析 ;(2)DM=4.
【分析】
(1)先证明两三角形全等,进一步得到BD=DE(2)根据M是BC的中点结合(1)的结论求DM的长.
【详解】
(1)证明:在△ABC 中,AD 平分∠BAC,BD⊥AD
(2)解:在△ABC 中,点 M 是边 BC 的中点,AB=12,AC=20.
【点睛】
此题重点考察学生对三角形全等的判定的应用,熟练掌握三角形全等的判定方法是解题的关键.
一、单选题
1.若,则下列式子错误的是( ).
A. B. C. D.
2.等腰三角形是轴对称图形,它的对称轴是( )
A.中线 B.底边上的中线 C.中线所在的直线 D.底边上的中线所在的直线
3.如图,在中,的垂直平分线交于点,平分,若,则的度数为( )
A. B. C. D.
4.若关于x的方程有增根,则k的值为( ).
A.3 B.1 C.0 D.-1
5.若,则的大小关系是 ( )
A. B. C. D.
6.某商品的进价是500元,标价是750元,商店要求以利润率为5%的售价打折出售,售货员可以打几折出售此商品( )
A.5 B.6 C.7 D.8
7.如图,中,,将绕点A按顺时针方向旋转,得到,则的度数为( )
A. B. C. D.
8.甲、乙两地之间的高速公路全长200千米,比原来国道的长度减少了20千米.高速公路通车后,某长途汽车的行驶速度提高了45千米/时,从甲地到乙地的行驶时间缩短了一半.设该长途汽车在原来国道上行驶的速度为x千米/时,根据题意,下列方程正确的是( )
A. B.
C. D.
9.一个正多边形的内角和等于1080°,这个正多边形的每个外角是( )
A.30° B.45° C.60° D.75°
10.关于的不等式组,有四个整数解,则的取值范围是( )
A. B. C. D.
二、填空题
11.如图,点P是∠AOB平分线OC上一点,PD⊥OB,垂足为D,若PD=2,则点P到边OA的距离是_____.
12.一个正多边形的内角和是外角和的3倍,则这个正多边形的一个内角的度数是______度.
13.某校组织开展了“诗词大会”的知识竞赛初赛,共有 20 道题. 答对一题加 10 分,答错 或不答一题扣 5 分,小辉在初赛得分超过 160 分顺利进入决赛. 设他答对 x 道题,根据题意,可列出关于 x 的不等式为 __________.
14.若分式的值为0,则x的值为_______.
15.一次函数y=ax+b与正比例函数y=kx在同一平面直角坐标系的图象如图所示,则关于x的不等式ax+b≥kx的解集为______.
16.如图,在四边形中,点是对角线的中点,点、分别是、的中点,,,则的度数是______.
17.如图,平行四边形ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB丁点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列四个结论:①∠ACD=30°;②;③=AC·AD;④OE:OA=1:其中结论正确的序号是____.(把所有正确结论的序号都选上)
三、解答题
18.如图,在平行四边形ABCD中,按以下步骤作图:
①以A为圆心,任意长为半径作弧,分别交AB,AD于点M,N;
②分别以M,N为圆心,以大于MN的长为半径作弧,两弧相交于点P;
③作AP射线,交边CD于点Q.
若QC=1,BC=3,则平行四边形ABCD周长为_____
19.解方程:? ? ? ? ? ? ? ??
20.化简并求值:(1-)÷,其中x=-1
21.因式分解:
(1);
(2).
22.如图,在?ABCD中,点E,F在AC上,且∠ABE=∠CDF,求证:BE=DF.
23.在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣4,5),C(﹣5,2).
(1)画出△ABC关于原点O成中心对称的△A1B1C1;
(2)写出△A1B1C1的顶点坐标;
(3)求出△A1B1C1的面积.
24.如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10,将△APB绕点B逆时针旋转一定角度后,可得到△CQB.
(1)求点P与点Q之间的距离;?
(2)求∠APB的度数.
25.已知:如图,,EF垂直平分,与,,分别交于点,,.
求证:(1)≌;
(2).
26.如图,在△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,点F在AC上,BE=FC.求证:BD=DF.
27.端午节是我国的传统节日,人们素有吃粽子的习俗,某商场在端午节来临之际用3000元购进、两种粽子1100个,购买种粽子与购买种粽子的费用相同,已知粽子的单价是种粽子单价的1.2倍.
(1)求、两种粽子的单价各是多少?
(2)若计划用不超过7000元的资金再次购买、两种粽子共2600个,已知、两种粽子的进价不变,求中粽子最多能购进多少个?
28.如图,四边形四条边上的中点分别为、、、,顺次连接、、、,得到四边形.求证:四边形是平行四边形.
29.在△ABC 中,点 M 是边 BC 的中点,AD 平分∠BAC,BD⊥AD,BD 的延长线交 AC 于点 E, AB=12,AC=20.
(1)求证:BD=DE;
(2)求 DM 的长.
参考答案
1.D
【分析】
利用不等式的性质判断即可得到结果.
【详解】
解:若x>y,
则有x-3>y-3; ;-2x<-2y; 3-x<3-y
故选D.
【点睛】
本题考查不等式的性质,熟练掌握不等式的性质是解本题的关键.
2.D
【分析】
根据等腰三角形的三线合一的性质,可得出答案.
【详解】
解:等腰三角形的对称轴是顶角的角平分线所在直线,底边高所在的直线,底边中线所在直线,
A、中线,错误;
B、底边上的中线,错误;
C、中线所在的直线,错误;
D、底边上的中线所在的直线,正确.
故选D.
【点睛】
本题考查了轴对称图形的知识,解答本题的关键是掌握轴对称及对称轴的定义.
3.B
【分析】
根据垂直平分线的性质和角平分线的定义求得∠ACB的度数,再根据三角形内角和求出∠B的度数.
【详解】
解:∵DE是AC的垂直平分线,
∴AD=CD,∠ACD=∠A=50°,
∵平分,
∴∠ACB=2∠ACD=100°,
∴∠B=180°-100°-50°=30°,
故选:B.
【点睛】
本题考查垂直平分线的性质、角平分线的定义和三角形内角和定理,熟练掌握垂直平分线的性质和角平分线的定义是解题的关键.
4.A
【解析】
试题解析:首先根据解分式方程的方法求出x的值,然后根据增根为x=1代入方程求出k的值.将方程的两边同时乘以(x-1)可得:3=x-1+k,解得:x=4-k,根据方程有增根可得:x=1,即4-k=1,k=3.
5.B
【分析】
根据时,可得越平方越小,,从而得到大小关系式.
【详解】
,
,,
,
故选:B.
【点睛】
本题考查了简单的实数的比较,可利用特殊值法即可比较大小,也可利用当时,的指数越大则数值越小解题.
6.C
【分析】
设售货员可以打x折出售此商品,根据:标价×-进价=进价×5%即可得出关于x的一元一次方程,解之即可得出结论.
【详解】
设售货员可以打x折出售此商品,
根据题意得:750×﹣500=500×5%,
解得:x=7,即售货员可以打7折出售此商品.
故选C.
【点睛】
本题考查了一元一次方程的应用,知道:商品的实际售价=商品标价×,找准等量关系,正确列出一元一次方程是解题的关键.
7.A
【分析】
根据∠BAC′=∠CAC′-∠CAB计算即可解决问题.
【详解】
∵∠CAC′=70°,∠CAB=36°,
∴∠BAC′=∠CAC′-∠CAB=70°-36°=34°,
故选:A.
【点睛】
本题考查了旋转变换,角的和差定义等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
8.B
【解析】
试题分析:设该长途汽车在原来国道上行驶的速度为x千米/时,根据题意得
.
故选B.
考点:由实际问题抽象出分式方程.
9.B
【分析】
首先设此多边形为n边形,根据题意得:180(n-2)=1080,即可求得n=8,再由多边形的外角和等于360°,即可求得答案.
【详解】
解:设此多边形为n边形,
根据题意得:180(n-2)=1080,
解得:n=8,
∴这个正多边形的每一个外角等于:360°÷8=45°.
故选:B.
【点睛】
此题考查了多边形的内角和与外角和的知识.注意掌握多边形内角和定理:(n-2)?180°,外角和等于360°.
10.A
【分析】
先求出不等式组中每个不等式的解集,然后求出其公共解集,最后求其整数解进而求a的取值范围.
【详解】
解:解不等式3x>2x+1,
得:x>1,
解不等式2-x>a,
得:x<2-a,
则不等式组的解集为1
∴5<2-a≤6,
解得:,
故选:A.
【点睛】
本题考查不等式组的解法及整数解的确定,求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了,掌握知识点是解题关键.
11.2
【分析】
作PE⊥OA,再根据角平分线的性质得出PE=PD即可得出答案.
【详解】
过P作PE⊥OA于点E,
∵点P是∠AOB平分线OC上一点,PD⊥OB,
∴PE=PD,
∵PD=2,
∴PE=2,
∴点P到边OA的距离是2.
故答案为2.
【点睛】
本题考查角平分线的性质,关键在于牢记角平分线的性质并灵活运用.
12.135
【分析】
先由多边形的内角和和外角和的关系判断出多边形的边数,即可得到结论.
【详解】
设多边形的边数为n.
因为正多边形内角和为(n?2)?180°,正多边形外角和为360°,
根据题意得:(n?2)?180°=360°×3,
解得:n=8.
∴这个正多边形的每个外角==45°,
则这个正多边形的每个内角是180°?45°=135°,
故答案为:135.
【点睛】
本题考查了正多边形的内角与外角,正多边形的性质;熟练掌握正多边形的性质,求出正多边形的边数是解决问题的关键.
13.
【分析】
竞赛得分=10×答对的题数-5×未答对的题数,根据本次竞赛得分要超过160分,列出不等式即可.
【详解】
解:设答对x道题,则答错(20-x)道,根据题意可得
.
故答案为.
点睛:本题考查了一元一次不等式在实际问题的应用,解决此类问题的关键是在理解题意的基础上,建立与之相应的解决问题的“数学模型”——不等式,再由不等式的相关知识确定问题的答案.
14.-3
【分析】
根据分式的值为零的条件可以求出x的值.
【详解】
解:根据题意得:,
解得:x=-3.
故答案为:-3.
【点睛】
若分式的值为零,需同时具备两个条件:(1)分子为0;(2)分母不为0.这两个条件缺一不可.
15.x≥﹣1
【分析】
由图象可以知道,当x=-1时,两个函数的函数值是相等的,再根据函数的增减性可以判断出不等式ax+b≥kx解集.
【详解】
两个条直线的交点坐标为(?1, 2),且当x≥?1时,直线y=kx在y=ax+b直线的下方,故不等式ax+b≥kx的解集为x≥?1.
故答案为x≥?1.
【点睛】
本题考查了一次函数与一元一次不等式的知识点,解题的关键是根据图象可知一次函数与一元一次不等式的增减性.
16.
【分析】
根据中位线定理推出PE=AD,PF=BC,由此得到PE=PF,推出△PEF是等腰三角形,根据三角形的内角和定理求出答案.
【详解】
∵点是对角线的中点,点、分别是、的中点,
∴PE=AD,PF=BC,
∵,
∴PE=PF,
∴△PEF是等腰三角形,
∴∠PFE=,
∴=,
故答案为:.
【点睛】
此题考查三角形的中位线定义及定理,等腰三角形的判定及性质,三角形的内角和定理,熟记三角形的中位线的定义及定理是解题的关键.
17.①②③④
【分析】
由四边形ABCD是平行四边形,得到∠ABC=∠ADC=60°,∠BAD=120°,根据角平分线的定义得到∠DCE=∠BCE=60°推出△CBE是等边三角形,证得∠ACB=90°,求出∠ACD=∠CAB=30°,故①正确;由AC⊥BC,得到S?ABCD=AC?BC,故③正确,根据直角三角形的性质得到AC=BC,根据三角形的中位线的性质得到OE=BC,AE=BE,于是得到②④正确.
【详解】
∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC=60°,∠BAD=120°,
∵CE平分∠BCD交AB于点E,
∴∠DCE=∠BCE=60°
∴△CBE是等边三角形,
∴BE=BC=CE,
∵AB=2BC,
∴AE=BC=CE,
∴∠ACB=90°,
∴∠ACD=∠CAB=30°,故①正确;
∵AC⊥BC,
∴=AC·AD,故③正确,
在Rt△ACB中,∠ACB=90°,∠CAB=30°,
∴AC=BC,
∵AO=OC,AE=BE,
∴OE=BC,OA=BC,
∴OE:OA==,
故④正确;
∵AE=BE,∴S△AOE=S△OBE,故②正确;
答案为:①②③④
【点睛】
此题考查了平行四边形的性质、三角形中位线的性质以及等边三角形的判定与性质.注意证得△BCE是等边三角形,OE是△ABC的中位线是关键.
18.14
【分析】
根据角平分线的性质可知∠DAQ=∠BAQ,再由平行四边形的性质得出CD∥AB,BC=AD=3,∠BAQ=∠DQA,故可得出△AQD是等腰三角形,据此可得出DQ=AD,进而可得出平行四边形ABCD周长.
【详解】
解:如图:
∵由作图可知,AQ是∠DAB的平分线,
∴∠DAQ=∠BAQ.
∵四边形ABCD是平行四边形,
∴CD∥AB,BC=AD=3,∠BAQ=∠DQA,
∴∠DAQ=∠DQA,
∴△AQD是等腰三角形,
∴DQ=AD=3.
∵QC=1,
∴CD=DQ+CQ=3+1=4,
∴平行四边形ABCD周长=2(DC+AD)=2×(4+3)=14.
故答案为:14.
【点睛】
本题考查的是复杂作图,解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.
19.;
【分析】
根据解分式方程的一般步骤解方程即可求解.
【详解】
解:?
方程两边同乘以(x-2)得 ,
,
,
,
检验:当时,,
所以是原分式方程的解;
解:方程两边同时乘以x(x-2)得 ,
解得 ,
检验:当时,x(x-2)≠0,
所以,原分式方程的解为.
【点睛】
本题考查了分式方程的解法,解分式方程的一般步骤是去分母化为整式方程,解整式方程,检验三步骤.
20.原式=
【分析】
原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把x的值代入计算即可求出值.
【详解】
解:
当时,原式
【点睛】
此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.
21.(1);(2)
【分析】
(1)利用平方差公式分解因式即可;
(2)直接提取公因式2y,再利用完全平方公式分解因式即可.
【详解】
(1);
(2).
【点睛】
本题考查提取公因式法以及公式法分解因式,正确应用公式是解题关键.
22.证明见解析.
【分析】
利用ASA即可得证;
【详解】
∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∵AB∥CD,∴∠BAE=∠DCF
∴在△ABE和△CDF中,,∴△ABE≌△CDF,∴BE=DF.
考点:1.平行四边形的性质;2.三角形全等的判定与性质.
23.(1)答案见解析;(2)点A1(2,﹣1)、B1(4,﹣5)、C1(5,﹣2);(3)5.
【解析】
试题分析:(1)分别作出点A、B、C关于原点O的对称点,再顺次连接即可;
(2)根据所作图形得出答案即可;
(3)利用割补法求解即可.
试题解析:解:(1)如图所示,△A1B1C1即为所求;
(2)点A1(2,﹣1)、B1(4,﹣5)、C1(5,﹣2);
(3)=3×4﹣×1×3﹣×2×4﹣×1×3=5.
点睛:本题主要考查作图-旋转变换,解题的关键是根据旋转的性质作出变换后的对应点及割补法求三角形的面积.
24.(1)6;(2)150°
【解析】
试题分析:先根据等边三角形的性质得AB=AC,∠BAC=60°,再利用旋转的性质得∠P′AP=∠BAC=60°,AP′=AP,BP′=CP=13,于是可判断△AP′P为等边三角形,得到PP′=AP=5,∠APP′=60°,接着根据勾股定理的逆定理证明△BPP′为直角三角形,且∠BPP′=90°,然后利用∠APB=∠APP′+∠BPP′求出∠APB的度数.
试题解析:∵△ABC为等边三角形,∴AB=AC,∠BAC=60°,
∵△PAC绕点A逆时针旋转后,得到△P′AB,
∴∠P′AP=∠BAC=60°,AP′=AP,BP′=CP=13,
∴△AP′P为等边三角形,
∴PP′=AP=5,∠APP′=60°,
在△BPP′中,∵PP′=5,BP=12,BP′=13,
∴PP′2+BP2=BP′2,
∴△BPP′为直角三角形,∠BPP′=90°,
∴∠APB=∠APP′+∠BPP′=60°+90°=150°.
答:点P与点P′之间的距离为5,∠APB的度数为150°.
【考点】旋转的性质;勾股定理的逆定理.
25.(1)见解析;(2)见解析
【分析】
(1)利用AAS判定即可;
(2)根据△BOF≌△DOE得到OE=OF,由,推出BD是EF的垂直平分线,由此得到结论.
【详解】
证明:(1),
,
垂直平分BD,
,,
在和中
≌;
(2)由(1)可知≌,
,且,
为线段EF的垂直平分线,
.
【点睛】
此题考查全等三角形的判定及性质,线段垂直平分线的判定及性质,熟记定理是解题的关键.
26.详见解析.
【分析】
因为∠C=90°,DE⊥AB,所以∠C=∠DEB,根据角平分线的性质得到CD=DE,根据SAS判定△DCF≌△DEB,根据全等三角形的性质即可得到结论.
【详解】
∵AD平分∠BAC,DE⊥AB,∠C=90°,
∴DC=DE.
在△DCF和△DEB中,
∵,
∴△DCF≌△DEB(SAS),
∴BD=DF.
【点睛】
本题考查了角平分线的性质,全等三角形的判定和性质,熟练掌握全等三角形的判定和性质定理是解题的关键.
27.(l)种粽子的单价是3元,种粽子的单价是2.5元;(2)种粽子最多能购进1000个.
【分析】
(1)根据题意列出分式方程计算即可,注意根的验证.
(2)根据题意列出不等式即可,根据不等式的性质求解.
【详解】
(l)设种粽子的单价为元,则种粽子的单价为元
根据题意,得
解得:
经检验,是原方程的根
所以种粽子的单价是3元,种粽子的单价是2.5元
(2)设种粽子购进个,则购进种粽子个
根据题意,得
解得
所以,种粽子最多能购进1000个
【点睛】
本题主要考查分式方程的应用,关键在于分式方程的解需要验证.
28.见解析
【分析】
连接AC,根据三角形的中位线定理得到,,同理推出,,根据一组对边平行且相等的四边形是平行四边形得出四边形EFGH是平行四边形
【详解】
证明:连接AC.
是DC的中点,H是AD的中点,
,且,
同理可知,且,
,且,
四边形是平行四边形.
【点睛】
本题主要考查对三角形的中位线定理,平行四边形的判定,解题的关键是正确的构造三角形病正确的运用中位线定理,难度不大.
29.(1)见解析 ;(2)DM=4.
【分析】
(1)先证明两三角形全等,进一步得到BD=DE(2)根据M是BC的中点结合(1)的结论求DM的长.
【详解】
(1)证明:在△ABC 中,AD 平分∠BAC,BD⊥AD
(2)解:在△ABC 中,点 M 是边 BC 的中点,AB=12,AC=20.
【点睛】
此题重点考察学生对三角形全等的判定的应用,熟练掌握三角形全等的判定方法是解题的关键.
同课章节目录
