黑龙江省绥化市绥棱县2020-2021学年八年级上学期期末数学试题(五四学制)(Word版 含解析)
文档属性
| 名称 | 黑龙江省绥化市绥棱县2020-2021学年八年级上学期期末数学试题(五四学制)(Word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 586.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-15 14:42:59 | ||
图片预览




文档简介
2020-2021学年八年级上学期期末数学试题(五四学制)
一、单选题
1.第24届冬季奥林匹克运动会,将于2022年02月04日~2022年02月20日在中华人民共和国北京市和张家口市联合举行.在会徽的图案设计中,设计者常常利用对称性进行设计,下列四个图案是历届会徽图案上的一部份图形,其中不是轴对称图形的是( )
A. B. C. D.
2.下列运算中正确的是( )
A. B. C. D.
3.一个等腰三角形的两边长分别为4,8,则它的周长为( ).
A.12 B.16 C.16或20 D.20
4.如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC,将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是[来( )
A.SAS B.ASA C.AAS D.SSS
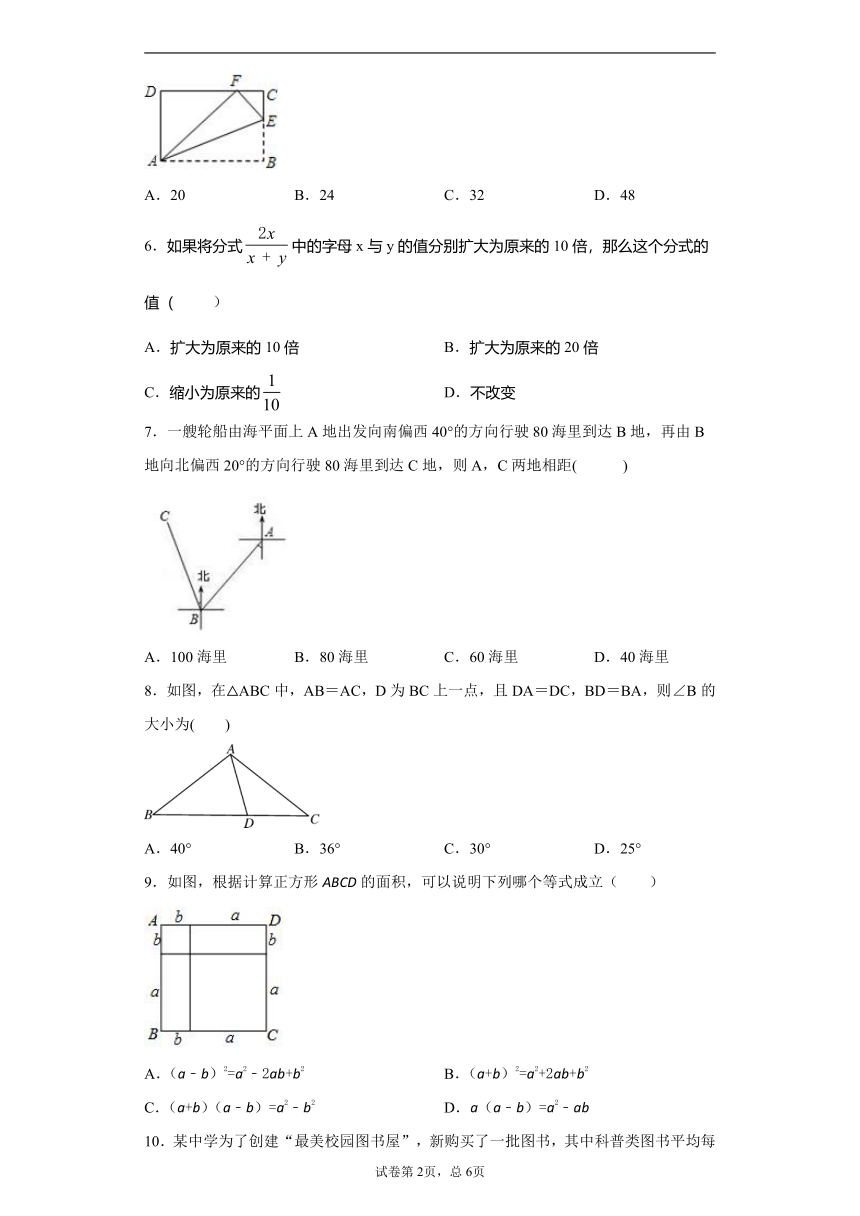
5.如图,将四边形纸片ABCD沿AE向上折叠,使点B落在DC边上的点F处若的周长为18,的周长为6,四边形纸片ABCD的周长为
A.20 B.24 C.32 D.48
6.如果将分式中的字母x与y的值分别扩大为原来的10倍,那么这个分式的值( )
A.扩大为原来的10倍 B.扩大为原来的20倍
C.缩小为原来的 D.不改变
7.一艘轮船由海平面上A地出发向南偏西40°的方向行驶80海里到达B地,再由B地向北偏西20°的方向行驶80海里到达C地,则A,C两地相距( )
A.100海里 B.80海里 C.60海里 D.40海里
8.如图,在△ABC中,AB=AC,D为BC上一点,且DA=DC,BD=BA,则∠B的大小为( )
A.40° B.36° C.30° D.25°
9.如图,根据计算正方形ABCD的面积,可以说明下列哪个等式成立( )
A.(a﹣b)2=a2﹣2ab+b2 B.(a+b)2=a2+2ab+b2
C.(a+b)(a﹣b)=a2﹣b2 D.a(a﹣b)=a2﹣ab
10.某中学为了创建“最美校园图书屋”,新购买了一批图书,其中科普类图书平均每本书的价格是文学类图书平均每本书价格的1.2倍.已知学校用12000元购买文学类图书的本数比用这些钱购买科普类图书的本数多100本,那么学校购买文学类图书平均每本书的价格是多少元?设学校购买文学类图书平均每本书的价格是x元,则下面所列方程中正确的是( )
A. B.
C. D.
二、填空题
11.新型冠状病毒的直径约为125纳米,1毫米=1000000纳米,125纳米用科学记数法表示为________毫米.
12.分解因式:=______.
13.如图,点B、F、C、E在一条直线上,已知BF=CE,AC∥DF,请你添加一个适当的条件______,使得△ABC≌△DEF.
14.要使式子有意义,则的取值范围是________.
15.若一个多边形的内角和与外角和之和是1800°,则此多边形是___边形.
16.已知等腰三角形一腰的垂直平分线与另一腰所在直线的夹角为40o,则此等腰三角形的顶角度数为__________
17.如果是完全平方式,则k的值是________ .
18.将一副三角板按图中方式叠放,那么两条最长边所夹锐角的度数是_____.
19.如图所示,小华从A点出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地A点时,一共走的路程是_____
20.如图所示,在中,,延长到,与的平分线相交于点,与的平分线相交于点,依此类推,与的平分线相交于点,则的度数是_________.
三、解答题
21.先化简,再求值:,其中,.
22.解分式方程:.
23.如图,在平面直角坐标系中,的三个顶点分别为,,.
(1)请在图中作出关于轴的轴对称图形(,,的对称点分别是,,),并直接写出,,的坐标.
(2)求的面积.
24.如图,已知中,,点在上.
(1)试用直尺和圆规在上找一点,使(不写作法,但需保留作图痕迹);
(2)在(1)的条件下,若;求证:.
25.问题探索:
(1)已知一个分数,如果分子、分母同时增加1,分数的值是增大还是减小?请说明你的理由.
(2)若正分数中分子和分母同时增加2,3,…,k(整数k>0),情况如何?
(3)请你用上面的结论解释下面的问题:
建筑学规定:民用住宅窗户面积必须小于地板面积,但按采光标准,窗户面积与地板面积的比应不小于10%,并且这个比值越大,住宅的采光条件越好,问:同时增加相等的窗户面积和地板面积,住宅的采光条件是变好了,还是变坏了?请说明理由.
26.问题引入:
(1)如图①所示,中,点是和的平分线的交点,若,则______(用表示);不用说明理由,直接填空.
如图②所示,,,若,则_______(用表示)不用说明理由,直接填空.
(2)如图③所示,,,若,则______(用表示),填空并说明理由.
27.东营市某学校2015年在商场购买甲、乙两种不同足球,购买甲种足球共花费2000元,购买乙种足球共花费1400元,购买甲种足球数量是购买乙种足球数量的2倍,且购买一个乙种足球比购买一个甲种足球多花20元.
(1)求购买一个甲种足球、一个乙种足球各需多少元;
(2)2016年为响应习总书记“足球进校园”的号召,这所学校决定再次购买甲、乙两种足球共50个,恰逢该商场对两种足球的售价进行调整,甲种足球售价比第一次购买时提高了10%,乙种足球售价比第一次购买时降低了10%,如果此次购买甲、乙两种足球的总费用不超过2900元,那么这所学校最多可购买多少个乙种足球?
28.如图,在平面直角坐标系中,点、分别在、轴上,已知点的坐标为,且.
(1) (2) (3)
(1)求的长度;
(2)以为一边作等边,过点作,交的垂直平分线于点.求证:;
(3)在(2)的条件下,连接交于,求证:为的中点.
参考答案
1.D
【详解】
A、不是轴对称图形,故此选项正确;
B、是轴对称图形,故此选项错误;
C、是轴对称图形,故此选项错误;
D、是轴对称图形,故此选项错误;
故选A.
2.D
【分析】
直接利用合并同类项法则、单项式乘单项式法则、同底数幂的乘法法则以及积的乘方法则运算即可求出答案.
【详解】
解:(A),故错误;
(B),故错误;
(C),故错误;
(D) ,故D正确;
故选:.
【点睛】
本题考查了合并同类项法则、单项式乘单项式法则、同底数幂的乘法法则以及积的乘方法则的应用,熟练运用运算法则是解决本题的关键.
3.D
【分析】
由于题中没有指明哪边是底哪边是腰,则应该分两种情况进行分析,然后根据三角形三边关系进行判断.
【详解】
解:①当4为腰时,4+4=8,故此种情况不存在;
②当8为腰时,8-4<8<8+4,符合题意.
故此三角形的周长=8+8+4=20.
故选:D.
【点睛】
本题考查的是等腰三角形的性质和三边关系,解答此题时注意分类讨论,不要漏解.
4.D
【解析】
试题解析:在△ADC和△ABC中,
,
∴△ADC≌△ABC(SSS),
∴∠DAC=∠BAC,
即∠QAE=∠PAE.
故选D.
5.B
【分析】
根据折叠的性质易知矩形ABCD的周长等于△AFD和△CFE的周长的和.
【详解】
由折叠的性质知,AF=AB,EF=BE.
所以矩形的周长等于△AFD和△CFE的周长的和为18+6=24cm.
故矩形ABCD的周长为24cm.
故答案为B.
【点睛】
本题考查了折叠的性质,解题关键是折叠前后图形的形状和大小不变,对应边和对应角相等.
6.D
【分析】
根据分式的基本性质即可求出答案.
【详解】
解:原式=
故选D.
【点睛】
本题考查分式的基本性质,解题的关键是熟练运用分式的基本性质,本题属于基础
题型.
7.B
【解析】
试题分析:连接AC,根据题意可得△ABC为等边三角形,则AC=80海里.
考点:等边三角形的性质
8.B
【分析】
根据AB=AC可得∠B=∠C,CD=DA可得∠ADB=2∠C=2∠B,BA=BD,可得∠BDA=∠BAD=2∠B,在△ABD中利用三角形内角和定理可求出∠B.
【详解】
解:∵AB=AC,
∴∠B=∠C,
∵CD=DA,
∴∠C=∠DAC,
∵BA=BD,
∴∠BDA=∠BAD=2∠C=2∠B,
设∠B=α,则∠BDA=∠BAD=2α,
又∵∠B+∠BAD+∠BDA=180°,
∴α+2α+2α=180°,
∴α=36°,即∠B=36°,
故选B.
【点睛】
本题主要考查等腰三角形的性质,掌握等边对等角是解题的关键,注意三角形内角和定理和方程思想的应用.
9.B
【解析】
分析:根据正方形ABCD的面积=边长为a的正方形的面积+两个长为a,宽为b的长方形的面积+边长为b的正方形的面积,即可解答.
详解:据题意得: (a+b)2=a2+2ab+b2.
故选B.
点睛:本题主要考查了完全平方公式的几何背景,解题的关键是通过几何图形之间的数量关系对公式做出几何解释.
10.B
【分析】
首先设文学类图书平均每本的价格为x元,则科普类图书平均每本的价格为1.2x元,根据题意可得等量关系:学校用12000元购买文学类图书的本数比用这些钱购买科普类图书的本数多100本,根据等量关系列出方程,
【详解】
设学校购买文学类图书平均每本书的价格是x元,可得:
故选B.
【点睛】
此题主要考查了分式方程的应用,关键是正确理解题意,找出题目中的等量关系,列出方程.
11.
【分析】
绝对值小于1的数也可以利用科学记数法表示,一般形式为a×10-n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
【详解】
解:125纳米=0.000125毫米=毫米,
故答案为:.
【点睛】
本题考查用科学记数法表示绝对值小于1的数,一般形式为a×10-n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.
12.x(x+2)(x﹣2).
【解析】
试题分析:==x(x+2)(x﹣2).故答案为x(x+2)(x﹣2).
考点:提公因式法与公式法的综合运用;因式分解.
13.∠A=∠D(答案不唯一)
【解析】
试题解析:添加∠A=∠D.理由如下:
∵FB=CE,
∴BC=EF.
又∵AC∥DF,
∴∠ACB=∠DFE.
∴在△ABC与△DEF中,
,
∴△ABC≌△DEF(AAS).
考点:全等三角形的判定.
14.
【分析】
根据分式有意义的条件:分母不为零,列不等式即可.
【详解】
根据分母不为零得到不等式,
x-2≠0
解得,x≠2
故答案为:x≠2
【点睛】
本题考查了分式有意义的条件,按照题意列出不等式是解题关键.
15.十
【详解】
试题分析:设所求n边形边数为n,先根据多边形的外角和为360度得到多边形的内角和,再根据多边形的内角和公式,即可得到结果.
由题意得多边形的内角和为1800°-360°=1440°,
设所求n边形边数为n,则180°(n-2)=1440°,解得n=10,
则此多边形是十边形.
考点:本题考查的是多边形的内角和公式,多边形的外角和
点评:解答本题的关键是熟练掌握多边形的内角和公式:180°(n-2),任意多边形的外角和均是360度,与边数无关.
16.50o或130o
【分析】
分情况进行讨论:①等腰三角形为锐角三角形;②等腰三角形为钝角三角形,即可得出答案.
【详解】
①当等腰三角形为锐角三角形时
∵DE垂直平分AC,∠ADE=40°
∴∠AED=90°
∴∠A=180°-∠ADE-∠AED=50°
②当等腰三角形为钝角三角形时
∵DE垂直平分AB,∠ADE=40°
∴∠AED=90°
∴∠DAE=180°-∠ADE-∠AED=50°
∴∠CAB=180°-∠DAE=130°
故答案为:50°或130°
【点睛】
本题考查的是等腰三角形,容易忽略的是考虑该等腰三角形为钝角三角形.
17.±12
【分析】
根据完全平方公式即可得到结论.
【详解】
解:∵是完全平方公式,
∴=(x+6y)2或者=(x-6y)2,
∴k=+12或k=-12,
故答案为:±12.
【点睛】
本题考查完全平方公式,注意完全平方公式中间项是±2ab.
18.75°
【分析】
先根据直角三角板的性质求出∠1及∠2的度数,再根据三角形内角与外角的关系即可解答.
【详解】
如图,由题意,可得∠2=45°,∠1+∠2=90°,
∴∠1=90°﹣45°=45°,
∴∠α=∠1+30°=45°+30°=75°.
故答案为75°.
【点睛】
本题考查了解直角三角形,三角形外角的性质,掌握三角形的外角等于与它不相邻的两个内角的和是解题的关键.
19.150米
【分析】
由题意可知小华所走的路线为一个正多边形,根据多边形的外角和即可求出答案.
【详解】
解:∵360°÷24°=15,
∴他需要走15次才会回到原来的起点,即一共走了15×10=150(米).
?故答案为150米.
【点睛】
本题考查了多边形的外角和定理的应用,,熟练掌握任何一个多边形的外角和都是360°是解答本题的关键.
20.2.5度
【分析】
由∠A1CD=∠A1+∠A1BC,∠ACD=∠ABC+∠A,而A1B、A1C分别平分∠ABC和∠ACD,得到∠ACD=2∠A1CD,∠ABC=2∠A1BC,于是有∠A=2∠A1,同理可得∠A1=2∠A2,即∠A=22∠A2,因此推出∠A=25∠A5,而∠A=80°,即可求出∠A5.
【详解】
解:∵A1B、A1C分别平分∠ABC和∠ACD,
∴∠ACD=2∠A1CD,∠ABC=2∠A1BC,
∵∠A1CD=∠A1+∠A1BC,∠ACD=∠ABC+∠A,
∴∠A=2∠A1
同理可得∠A1=2∠A2,即∠A=22∠A2,
…,
∴∠A=25∠A5,
∵∠A=80°,
∴∠A5=80°÷32=2.5°.
故答案为:2.5°.
【点睛】
本题考查了三角形的内角和定理:三角形的内角和为180°.也考查了三角形的外角性质以及角平分线性质.
21.,
【分析】
将原式被除式分子利用平方差公式分解因式,分母提取a分解因式,约分后得到最简结果,除式中通分并利用同分母分式的加法法则计算,分子利用完全平方公式分解因式,同时利用除以一个数等于乘以这个数的倒数将除法运算化为乘法运算,约分后得到最简结果,将a与b的值代入化简后的式子中计算,即可得到原式的值.
【详解】
解:原式,
,
,
,
当,时,原式.
【点睛】
本题考查分式的化简求值,解题的关键是把分式化到最简,然后代值计算.
22.原分式方程的解为.
【分析】
分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
【详解】
解:
方程两边都乘以,得,
解得,
检验:当时,,
∴原分式方程的解为.
【点睛】
此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.
23.(1)答案见解析;,,;(2).
【分析】
(1)分别作出点A,B,C的对称点A′,B′,C′,顺次连接,然后再根据各点在坐标系中的位置写出坐标即可得;
(2)利用割补法求解可得.
【详解】
(1)如图所示.
,,
(2)如图,正方形ADEC?的面积为:5×5=25
△A?DE的面积为:
△A?AC?的面积为:
△BEC?的面积为:
【点睛】
本题主要考查轴对称变换的作图以及用割补法求三角形面积,熟练掌握轴对称变换的性质是解题的关键.
24.(1)如图所示.见解析;(2)见解析.
【分析】
(1)作∠CPD=∠BAP,则∠CPD的另一边与AC的交点即为所求作的点D;
(2)证明即可.
【详解】
解:(1)如图所示.
(2)∵
∴
∵
∴
∴.
【点睛】
此题主要考查了作一个角等于已知角,以及平行线的判定,熟练掌握判定定理是解答此题的关键.
25.(1) 分数的值增大,理由见解析;(2)<(m>n>0,k>0); (3)住宅的采光条件变好,理由见解析.
【分析】
(1)根据题意可得,只要判断-的正负即可;
(2)同理(1)只要判断-的正负即可;
(3)由(2)即可得到答案.
【详解】
.解:分数(m>n>0)中,若分子、分母同时增加1,分数的值增大.
理由如下:
-==,
∵m>n>0,
∴n-m<0,m(m+1)>0,即<0,
∴<,
∴分数(m>n>0)中,,若分子、分母同时增加1,分数的值增大;
(2) 若正分数中分子和分母同时增加k(整数k>0),分数值增大,
理由如下:
-==,
∵m>n>0,k>0,
∴<0,m(m+k)>0,
∴<0,
∴<(m>n>0,k>0);
(3)住宅的采光条件变好.
理由: 设原来的地板面积和窗户面积分别为x,y,增加面积为k,
则由(2)知>,所以住宅的采光条件变好了.
【点睛】
本题主要考查分式的加减运算,解此题的关键在于根据题意列出分式,然后化简判断正负即可.
26.(1),;(2),理由见解析
【分析】
(1)如图①,根据角平分线的定义可得∠OBC=∠ABC,∠OCB=∠ACB,然后表示出∠OBC+∠OCB,再根据三角形的内角和等于180°列式整理即可得∠BOC=;如图②,根据三角形的内角和等于180°列式整理即可得∠BOC=;
(2)如图③,根据三角形的内角和等于180°列式整理即可得∠BOC=.
【详解】
解:(1)如图①,∵∠ABC与∠ACB的平分线相交于点O,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∴∠OBC+∠OCB=(∠ABC+∠ACB),
在△OBC中,∠BOC=180°-(∠OBC+∠OCB)
=180°-(∠ABC+∠ACB)
=180°-(180°-∠A)
=90°+∠A
=;
如图②,在△OBC中,∠BOC=180°-(∠OBC+∠OCB)
=180°-(∠ABC+∠ACB)
=180°-(180°-∠A)
=120°+∠A
=;
(2).
理由:∵,,,,,
∴.
【点睛】
本题考查三角形的外角的性质,三角形的内角和定理等知识,解题的关键是熟练掌握基本知识.
27.(1)购买一个甲种足球需50元,购买一个乙种足球需70元;(2)这所学校最多可购买18个乙种足球.
【分析】
(1)设购买一个甲种足球需x元,则购买一个乙种足球需(x+20),根据购买甲种足球数量是购买乙种足球数量的2倍列出方程解答即可;
(2)设这所学校再次购买y个乙种足球,根据题意列出不等式解答即可.
【详解】
解:(1)设购买一个甲种足球需x元,则购买一个乙种足球需(x+20),可得:
,
解得:x=50,
经检验x=50是原方程的解.
答:购买一个甲种足球需50元,则购买一个乙种足球需70元.
(2)设这所学校再次购买y个乙种足球,可得:50×(1+10%)×(50﹣y)+70×(1﹣10%)y≤2900,
解得:y≤18.75,
由题意可得,最多可购买18个乙种足球,
答:这所学校最多可购买18个乙种足球.
28.(1);(2)详见解析;(3)详见解析.
【分析】
(1)根据含30°的直角三角形的性质即可求解;
(2)连接,得到是等边三角形,故,由得到,得到是等边三角形,可证得,即可求解;
(3)过点作,根据是等边三角形,得到,故, 得到,再证明,即可求解.
【详解】
解:(1)由点的坐标(0,1),,可得.
(2)连接,是等边三角形,
,
,
又,
,,
是等边三角形,,
,
(3)过点作,则
是等边三角形,
∴∠BAO=
又AB=EB,
,
∵EM∥AD,
∴∠MEF=∠ADF,又∠MFE=∠AFD
是的中点.
【点睛】
此题主要考查全等三角形的证明,解题的关键是熟知直角三角形的性质、全等三角形的判定与性质.
一、单选题
1.第24届冬季奥林匹克运动会,将于2022年02月04日~2022年02月20日在中华人民共和国北京市和张家口市联合举行.在会徽的图案设计中,设计者常常利用对称性进行设计,下列四个图案是历届会徽图案上的一部份图形,其中不是轴对称图形的是( )
A. B. C. D.
2.下列运算中正确的是( )
A. B. C. D.
3.一个等腰三角形的两边长分别为4,8,则它的周长为( ).
A.12 B.16 C.16或20 D.20
4.如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC,将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是[来( )
A.SAS B.ASA C.AAS D.SSS
5.如图,将四边形纸片ABCD沿AE向上折叠,使点B落在DC边上的点F处若的周长为18,的周长为6,四边形纸片ABCD的周长为
A.20 B.24 C.32 D.48
6.如果将分式中的字母x与y的值分别扩大为原来的10倍,那么这个分式的值( )
A.扩大为原来的10倍 B.扩大为原来的20倍
C.缩小为原来的 D.不改变
7.一艘轮船由海平面上A地出发向南偏西40°的方向行驶80海里到达B地,再由B地向北偏西20°的方向行驶80海里到达C地,则A,C两地相距( )
A.100海里 B.80海里 C.60海里 D.40海里
8.如图,在△ABC中,AB=AC,D为BC上一点,且DA=DC,BD=BA,则∠B的大小为( )
A.40° B.36° C.30° D.25°
9.如图,根据计算正方形ABCD的面积,可以说明下列哪个等式成立( )
A.(a﹣b)2=a2﹣2ab+b2 B.(a+b)2=a2+2ab+b2
C.(a+b)(a﹣b)=a2﹣b2 D.a(a﹣b)=a2﹣ab
10.某中学为了创建“最美校园图书屋”,新购买了一批图书,其中科普类图书平均每本书的价格是文学类图书平均每本书价格的1.2倍.已知学校用12000元购买文学类图书的本数比用这些钱购买科普类图书的本数多100本,那么学校购买文学类图书平均每本书的价格是多少元?设学校购买文学类图书平均每本书的价格是x元,则下面所列方程中正确的是( )
A. B.
C. D.
二、填空题
11.新型冠状病毒的直径约为125纳米,1毫米=1000000纳米,125纳米用科学记数法表示为________毫米.
12.分解因式:=______.
13.如图,点B、F、C、E在一条直线上,已知BF=CE,AC∥DF,请你添加一个适当的条件______,使得△ABC≌△DEF.
14.要使式子有意义,则的取值范围是________.
15.若一个多边形的内角和与外角和之和是1800°,则此多边形是___边形.
16.已知等腰三角形一腰的垂直平分线与另一腰所在直线的夹角为40o,则此等腰三角形的顶角度数为__________
17.如果是完全平方式,则k的值是________ .
18.将一副三角板按图中方式叠放,那么两条最长边所夹锐角的度数是_____.
19.如图所示,小华从A点出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地A点时,一共走的路程是_____
20.如图所示,在中,,延长到,与的平分线相交于点,与的平分线相交于点,依此类推,与的平分线相交于点,则的度数是_________.
三、解答题
21.先化简,再求值:,其中,.
22.解分式方程:.
23.如图,在平面直角坐标系中,的三个顶点分别为,,.
(1)请在图中作出关于轴的轴对称图形(,,的对称点分别是,,),并直接写出,,的坐标.
(2)求的面积.
24.如图,已知中,,点在上.
(1)试用直尺和圆规在上找一点,使(不写作法,但需保留作图痕迹);
(2)在(1)的条件下,若;求证:.
25.问题探索:
(1)已知一个分数,如果分子、分母同时增加1,分数的值是增大还是减小?请说明你的理由.
(2)若正分数中分子和分母同时增加2,3,…,k(整数k>0),情况如何?
(3)请你用上面的结论解释下面的问题:
建筑学规定:民用住宅窗户面积必须小于地板面积,但按采光标准,窗户面积与地板面积的比应不小于10%,并且这个比值越大,住宅的采光条件越好,问:同时增加相等的窗户面积和地板面积,住宅的采光条件是变好了,还是变坏了?请说明理由.
26.问题引入:
(1)如图①所示,中,点是和的平分线的交点,若,则______(用表示);不用说明理由,直接填空.
如图②所示,,,若,则_______(用表示)不用说明理由,直接填空.
(2)如图③所示,,,若,则______(用表示),填空并说明理由.
27.东营市某学校2015年在商场购买甲、乙两种不同足球,购买甲种足球共花费2000元,购买乙种足球共花费1400元,购买甲种足球数量是购买乙种足球数量的2倍,且购买一个乙种足球比购买一个甲种足球多花20元.
(1)求购买一个甲种足球、一个乙种足球各需多少元;
(2)2016年为响应习总书记“足球进校园”的号召,这所学校决定再次购买甲、乙两种足球共50个,恰逢该商场对两种足球的售价进行调整,甲种足球售价比第一次购买时提高了10%,乙种足球售价比第一次购买时降低了10%,如果此次购买甲、乙两种足球的总费用不超过2900元,那么这所学校最多可购买多少个乙种足球?
28.如图,在平面直角坐标系中,点、分别在、轴上,已知点的坐标为,且.
(1) (2) (3)
(1)求的长度;
(2)以为一边作等边,过点作,交的垂直平分线于点.求证:;
(3)在(2)的条件下,连接交于,求证:为的中点.
参考答案
1.D
【详解】
A、不是轴对称图形,故此选项正确;
B、是轴对称图形,故此选项错误;
C、是轴对称图形,故此选项错误;
D、是轴对称图形,故此选项错误;
故选A.
2.D
【分析】
直接利用合并同类项法则、单项式乘单项式法则、同底数幂的乘法法则以及积的乘方法则运算即可求出答案.
【详解】
解:(A),故错误;
(B),故错误;
(C),故错误;
(D) ,故D正确;
故选:.
【点睛】
本题考查了合并同类项法则、单项式乘单项式法则、同底数幂的乘法法则以及积的乘方法则的应用,熟练运用运算法则是解决本题的关键.
3.D
【分析】
由于题中没有指明哪边是底哪边是腰,则应该分两种情况进行分析,然后根据三角形三边关系进行判断.
【详解】
解:①当4为腰时,4+4=8,故此种情况不存在;
②当8为腰时,8-4<8<8+4,符合题意.
故此三角形的周长=8+8+4=20.
故选:D.
【点睛】
本题考查的是等腰三角形的性质和三边关系,解答此题时注意分类讨论,不要漏解.
4.D
【解析】
试题解析:在△ADC和△ABC中,
,
∴△ADC≌△ABC(SSS),
∴∠DAC=∠BAC,
即∠QAE=∠PAE.
故选D.
5.B
【分析】
根据折叠的性质易知矩形ABCD的周长等于△AFD和△CFE的周长的和.
【详解】
由折叠的性质知,AF=AB,EF=BE.
所以矩形的周长等于△AFD和△CFE的周长的和为18+6=24cm.
故矩形ABCD的周长为24cm.
故答案为B.
【点睛】
本题考查了折叠的性质,解题关键是折叠前后图形的形状和大小不变,对应边和对应角相等.
6.D
【分析】
根据分式的基本性质即可求出答案.
【详解】
解:原式=
故选D.
【点睛】
本题考查分式的基本性质,解题的关键是熟练运用分式的基本性质,本题属于基础
题型.
7.B
【解析】
试题分析:连接AC,根据题意可得△ABC为等边三角形,则AC=80海里.
考点:等边三角形的性质
8.B
【分析】
根据AB=AC可得∠B=∠C,CD=DA可得∠ADB=2∠C=2∠B,BA=BD,可得∠BDA=∠BAD=2∠B,在△ABD中利用三角形内角和定理可求出∠B.
【详解】
解:∵AB=AC,
∴∠B=∠C,
∵CD=DA,
∴∠C=∠DAC,
∵BA=BD,
∴∠BDA=∠BAD=2∠C=2∠B,
设∠B=α,则∠BDA=∠BAD=2α,
又∵∠B+∠BAD+∠BDA=180°,
∴α+2α+2α=180°,
∴α=36°,即∠B=36°,
故选B.
【点睛】
本题主要考查等腰三角形的性质,掌握等边对等角是解题的关键,注意三角形内角和定理和方程思想的应用.
9.B
【解析】
分析:根据正方形ABCD的面积=边长为a的正方形的面积+两个长为a,宽为b的长方形的面积+边长为b的正方形的面积,即可解答.
详解:据题意得: (a+b)2=a2+2ab+b2.
故选B.
点睛:本题主要考查了完全平方公式的几何背景,解题的关键是通过几何图形之间的数量关系对公式做出几何解释.
10.B
【分析】
首先设文学类图书平均每本的价格为x元,则科普类图书平均每本的价格为1.2x元,根据题意可得等量关系:学校用12000元购买文学类图书的本数比用这些钱购买科普类图书的本数多100本,根据等量关系列出方程,
【详解】
设学校购买文学类图书平均每本书的价格是x元,可得:
故选B.
【点睛】
此题主要考查了分式方程的应用,关键是正确理解题意,找出题目中的等量关系,列出方程.
11.
【分析】
绝对值小于1的数也可以利用科学记数法表示,一般形式为a×10-n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
【详解】
解:125纳米=0.000125毫米=毫米,
故答案为:.
【点睛】
本题考查用科学记数法表示绝对值小于1的数,一般形式为a×10-n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.
12.x(x+2)(x﹣2).
【解析】
试题分析:==x(x+2)(x﹣2).故答案为x(x+2)(x﹣2).
考点:提公因式法与公式法的综合运用;因式分解.
13.∠A=∠D(答案不唯一)
【解析】
试题解析:添加∠A=∠D.理由如下:
∵FB=CE,
∴BC=EF.
又∵AC∥DF,
∴∠ACB=∠DFE.
∴在△ABC与△DEF中,
,
∴△ABC≌△DEF(AAS).
考点:全等三角形的判定.
14.
【分析】
根据分式有意义的条件:分母不为零,列不等式即可.
【详解】
根据分母不为零得到不等式,
x-2≠0
解得,x≠2
故答案为:x≠2
【点睛】
本题考查了分式有意义的条件,按照题意列出不等式是解题关键.
15.十
【详解】
试题分析:设所求n边形边数为n,先根据多边形的外角和为360度得到多边形的内角和,再根据多边形的内角和公式,即可得到结果.
由题意得多边形的内角和为1800°-360°=1440°,
设所求n边形边数为n,则180°(n-2)=1440°,解得n=10,
则此多边形是十边形.
考点:本题考查的是多边形的内角和公式,多边形的外角和
点评:解答本题的关键是熟练掌握多边形的内角和公式:180°(n-2),任意多边形的外角和均是360度,与边数无关.
16.50o或130o
【分析】
分情况进行讨论:①等腰三角形为锐角三角形;②等腰三角形为钝角三角形,即可得出答案.
【详解】
①当等腰三角形为锐角三角形时
∵DE垂直平分AC,∠ADE=40°
∴∠AED=90°
∴∠A=180°-∠ADE-∠AED=50°
②当等腰三角形为钝角三角形时
∵DE垂直平分AB,∠ADE=40°
∴∠AED=90°
∴∠DAE=180°-∠ADE-∠AED=50°
∴∠CAB=180°-∠DAE=130°
故答案为:50°或130°
【点睛】
本题考查的是等腰三角形,容易忽略的是考虑该等腰三角形为钝角三角形.
17.±12
【分析】
根据完全平方公式即可得到结论.
【详解】
解:∵是完全平方公式,
∴=(x+6y)2或者=(x-6y)2,
∴k=+12或k=-12,
故答案为:±12.
【点睛】
本题考查完全平方公式,注意完全平方公式中间项是±2ab.
18.75°
【分析】
先根据直角三角板的性质求出∠1及∠2的度数,再根据三角形内角与外角的关系即可解答.
【详解】
如图,由题意,可得∠2=45°,∠1+∠2=90°,
∴∠1=90°﹣45°=45°,
∴∠α=∠1+30°=45°+30°=75°.
故答案为75°.
【点睛】
本题考查了解直角三角形,三角形外角的性质,掌握三角形的外角等于与它不相邻的两个内角的和是解题的关键.
19.150米
【分析】
由题意可知小华所走的路线为一个正多边形,根据多边形的外角和即可求出答案.
【详解】
解:∵360°÷24°=15,
∴他需要走15次才会回到原来的起点,即一共走了15×10=150(米).
?故答案为150米.
【点睛】
本题考查了多边形的外角和定理的应用,,熟练掌握任何一个多边形的外角和都是360°是解答本题的关键.
20.2.5度
【分析】
由∠A1CD=∠A1+∠A1BC,∠ACD=∠ABC+∠A,而A1B、A1C分别平分∠ABC和∠ACD,得到∠ACD=2∠A1CD,∠ABC=2∠A1BC,于是有∠A=2∠A1,同理可得∠A1=2∠A2,即∠A=22∠A2,因此推出∠A=25∠A5,而∠A=80°,即可求出∠A5.
【详解】
解:∵A1B、A1C分别平分∠ABC和∠ACD,
∴∠ACD=2∠A1CD,∠ABC=2∠A1BC,
∵∠A1CD=∠A1+∠A1BC,∠ACD=∠ABC+∠A,
∴∠A=2∠A1
同理可得∠A1=2∠A2,即∠A=22∠A2,
…,
∴∠A=25∠A5,
∵∠A=80°,
∴∠A5=80°÷32=2.5°.
故答案为:2.5°.
【点睛】
本题考查了三角形的内角和定理:三角形的内角和为180°.也考查了三角形的外角性质以及角平分线性质.
21.,
【分析】
将原式被除式分子利用平方差公式分解因式,分母提取a分解因式,约分后得到最简结果,除式中通分并利用同分母分式的加法法则计算,分子利用完全平方公式分解因式,同时利用除以一个数等于乘以这个数的倒数将除法运算化为乘法运算,约分后得到最简结果,将a与b的值代入化简后的式子中计算,即可得到原式的值.
【详解】
解:原式,
,
,
,
当,时,原式.
【点睛】
本题考查分式的化简求值,解题的关键是把分式化到最简,然后代值计算.
22.原分式方程的解为.
【分析】
分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
【详解】
解:
方程两边都乘以,得,
解得,
检验:当时,,
∴原分式方程的解为.
【点睛】
此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.
23.(1)答案见解析;,,;(2).
【分析】
(1)分别作出点A,B,C的对称点A′,B′,C′,顺次连接,然后再根据各点在坐标系中的位置写出坐标即可得;
(2)利用割补法求解可得.
【详解】
(1)如图所示.
,,
(2)如图,正方形ADEC?的面积为:5×5=25
△A?DE的面积为:
△A?AC?的面积为:
△BEC?的面积为:
【点睛】
本题主要考查轴对称变换的作图以及用割补法求三角形面积,熟练掌握轴对称变换的性质是解题的关键.
24.(1)如图所示.见解析;(2)见解析.
【分析】
(1)作∠CPD=∠BAP,则∠CPD的另一边与AC的交点即为所求作的点D;
(2)证明即可.
【详解】
解:(1)如图所示.
(2)∵
∴
∵
∴
∴.
【点睛】
此题主要考查了作一个角等于已知角,以及平行线的判定,熟练掌握判定定理是解答此题的关键.
25.(1) 分数的值增大,理由见解析;(2)<(m>n>0,k>0); (3)住宅的采光条件变好,理由见解析.
【分析】
(1)根据题意可得,只要判断-的正负即可;
(2)同理(1)只要判断-的正负即可;
(3)由(2)即可得到答案.
【详解】
.解:分数(m>n>0)中,若分子、分母同时增加1,分数的值增大.
理由如下:
-==,
∵m>n>0,
∴n-m<0,m(m+1)>0,即<0,
∴<,
∴分数(m>n>0)中,,若分子、分母同时增加1,分数的值增大;
(2) 若正分数中分子和分母同时增加k(整数k>0),分数值增大,
理由如下:
-==,
∵m>n>0,k>0,
∴<0,m(m+k)>0,
∴<0,
∴<(m>n>0,k>0);
(3)住宅的采光条件变好.
理由: 设原来的地板面积和窗户面积分别为x,y,增加面积为k,
则由(2)知>,所以住宅的采光条件变好了.
【点睛】
本题主要考查分式的加减运算,解此题的关键在于根据题意列出分式,然后化简判断正负即可.
26.(1),;(2),理由见解析
【分析】
(1)如图①,根据角平分线的定义可得∠OBC=∠ABC,∠OCB=∠ACB,然后表示出∠OBC+∠OCB,再根据三角形的内角和等于180°列式整理即可得∠BOC=;如图②,根据三角形的内角和等于180°列式整理即可得∠BOC=;
(2)如图③,根据三角形的内角和等于180°列式整理即可得∠BOC=.
【详解】
解:(1)如图①,∵∠ABC与∠ACB的平分线相交于点O,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∴∠OBC+∠OCB=(∠ABC+∠ACB),
在△OBC中,∠BOC=180°-(∠OBC+∠OCB)
=180°-(∠ABC+∠ACB)
=180°-(180°-∠A)
=90°+∠A
=;
如图②,在△OBC中,∠BOC=180°-(∠OBC+∠OCB)
=180°-(∠ABC+∠ACB)
=180°-(180°-∠A)
=120°+∠A
=;
(2).
理由:∵,,,,,
∴.
【点睛】
本题考查三角形的外角的性质,三角形的内角和定理等知识,解题的关键是熟练掌握基本知识.
27.(1)购买一个甲种足球需50元,购买一个乙种足球需70元;(2)这所学校最多可购买18个乙种足球.
【分析】
(1)设购买一个甲种足球需x元,则购买一个乙种足球需(x+20),根据购买甲种足球数量是购买乙种足球数量的2倍列出方程解答即可;
(2)设这所学校再次购买y个乙种足球,根据题意列出不等式解答即可.
【详解】
解:(1)设购买一个甲种足球需x元,则购买一个乙种足球需(x+20),可得:
,
解得:x=50,
经检验x=50是原方程的解.
答:购买一个甲种足球需50元,则购买一个乙种足球需70元.
(2)设这所学校再次购买y个乙种足球,可得:50×(1+10%)×(50﹣y)+70×(1﹣10%)y≤2900,
解得:y≤18.75,
由题意可得,最多可购买18个乙种足球,
答:这所学校最多可购买18个乙种足球.
28.(1);(2)详见解析;(3)详见解析.
【分析】
(1)根据含30°的直角三角形的性质即可求解;
(2)连接,得到是等边三角形,故,由得到,得到是等边三角形,可证得,即可求解;
(3)过点作,根据是等边三角形,得到,故, 得到,再证明,即可求解.
【详解】
解:(1)由点的坐标(0,1),,可得.
(2)连接,是等边三角形,
,
,
又,
,,
是等边三角形,,
,
(3)过点作,则
是等边三角形,
∴∠BAO=
又AB=EB,
,
∵EM∥AD,
∴∠MEF=∠ADF,又∠MFE=∠AFD
是的中点.
【点睛】
此题主要考查全等三角形的证明,解题的关键是熟知直角三角形的性质、全等三角形的判定与性质.
同课章节目录
