上海市嘉定区2020-2021学年九年级上学期期末数学试题(Word版 含答案)
文档属性
| 名称 | 上海市嘉定区2020-2021学年九年级上学期期末数学试题(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1008.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-15 16:19:08 | ||
图片预览


文档简介
嘉定区2020学年第一学期九年级期未质量调研
数学试卷
(满分150分,考试时间100分钟)
同学们注意:
1.本试卷含三个大题,共25题;没有特殊说明,几何题均视为在同一个平面内研究问题.
2.答题时,务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效;
3.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.
一、选择题:(本大题共6题,每题4分,满分24分)
【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上.】
1.如果实数a,b,c,d满足,下列四个选项中,正确的是( )
A. B. C. D.
2.在平面直角坐标系中,已知点,点P与原点O的连线与x轴的正半轴的夹角为,那么的值是( )
A. B. C. D.3
3.抛物线的顶点坐标是( )
A. B. C. D.
4.已知单位向量与非零向量、,下列四个选项中,正确的是( )
A. B. C. D.
5.在中,,,,垂足为D.下列四个选项中,不正确的是( )
A. B. C. D.
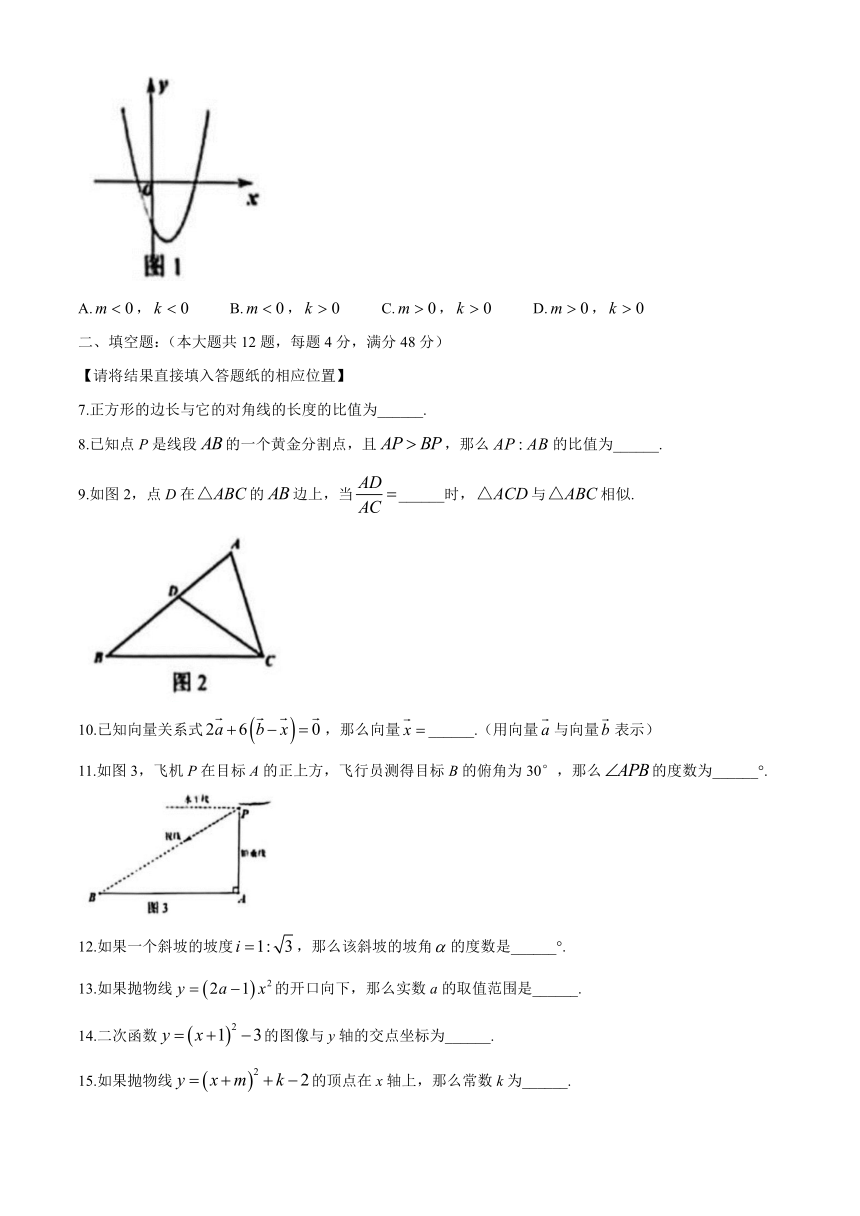
6.二次函数的图像如图l所示,下列四个选项中,正确的是( )
A., B., C., D.,
二、填空题:(本大题共12题,每题4分,满分48分)
【请将结果直接填入答题纸的相应位置】
7.正方形的边长与它的对角线的长度的比值为______.
8.已知点P是线段的一个黄金分割点,且,那么的比值为______.
9.如图2,点D在的边上,当______时,与相似.
10.已知向量关系式,那么向量______.(用向量与向量表示)
11.如图3,飞机P在目标A的正上方,飞行员测得目标B的俯角为30°,那么的度数为______°.
12.如果一个斜坡的坡度,那么该斜坡的坡角的度数是______°.
13.如果抛物线的开口向下,那么实数a的取值范围是______.
14.二次函数的图像与y轴的交点坐标为______.
15.如果抛物线的顶点在x轴上,那么常数k为______.
16.如果抛物线的对称轴是直线,那么______0.(从<,=,>中选择)
17.如图4,正方形和正方形的边长相等,点A、B、C在同一条直线上.联结、,那么的值为______.
18.已知在中,,,(如图5),把绕着点C按顺时针方向旋转.将点A、B的对应点分别记为点、,如果为直角三角形,那么点A与点的距离为______.
三、解答题:(本大题共7题,满分78分)
19.(本题满分10分)
计算:
20.(本题满分10分,第(l)小题满分4分,第(2)小题满分6分)
我们已经知道二次函数的图像是一条抛物线.研究二次函数的图像与性质,我们主要关注抛物线的对称轴、抛物线的开口方向、抛物线的最高点(或最低点)的坐标、抛物线与坐标轴的交点坐标、抛物线的上升或下降情况(沿x轴的正方向看).
已知一个二次函数的大致图像如图6所示.
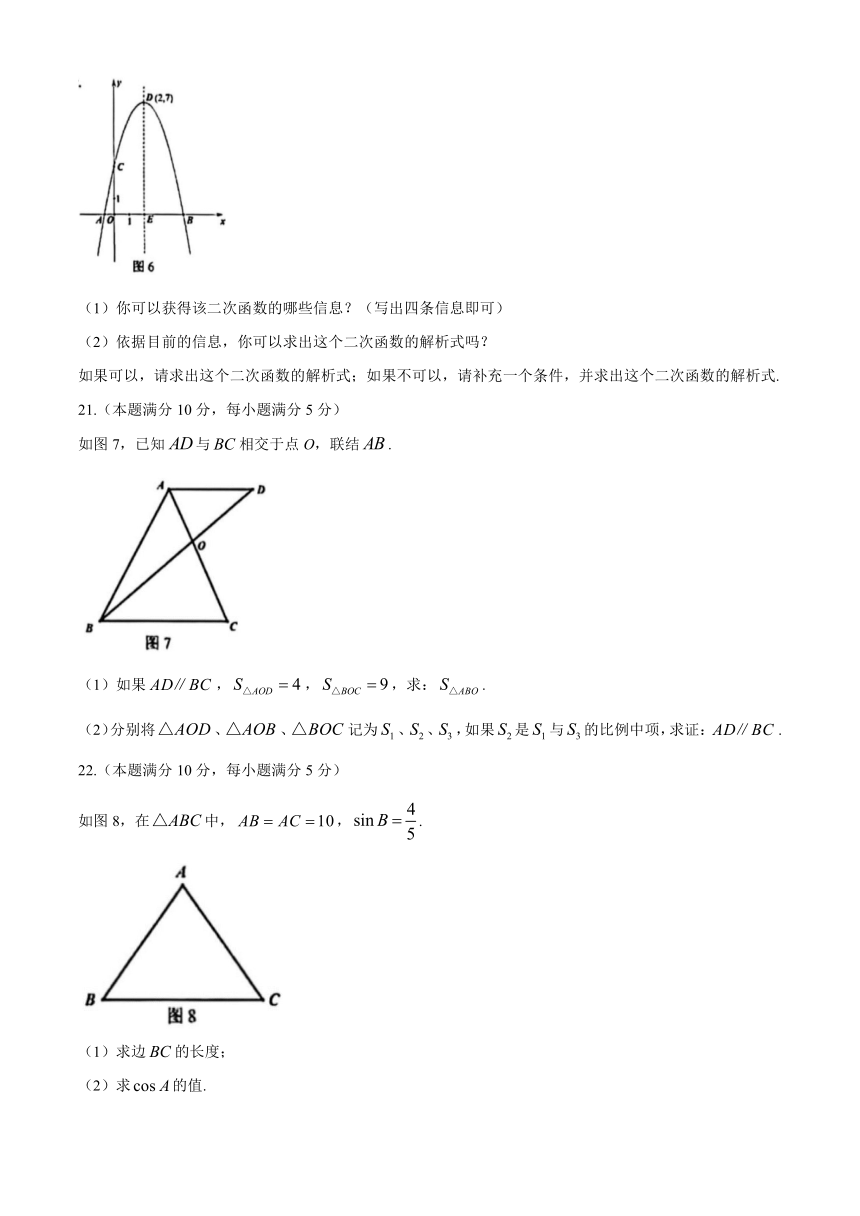
(1)你可以获得该二次函数的哪些信息?(写出四条信息即可)
(2)依据目前的信息,你可以求出这个二次函数的解析式吗?
如果可以,请求出这个二次函数的解析式;如果不可以,请补充一个条件,并求出这个二次函数的解析式.
21.(本题满分10分,每小题满分5分)
如图7,已知与相交于点O,联结.
(1)如果,,,求:.
(2)分别将、、记为、、,如果是与的比例中项,求证:.
22.(本题满分10分,每小题满分5分)
如图8,在中,,.
(1)求边的长度;
(2)求的值.
23.(本题满分12分,每小题满分6分)
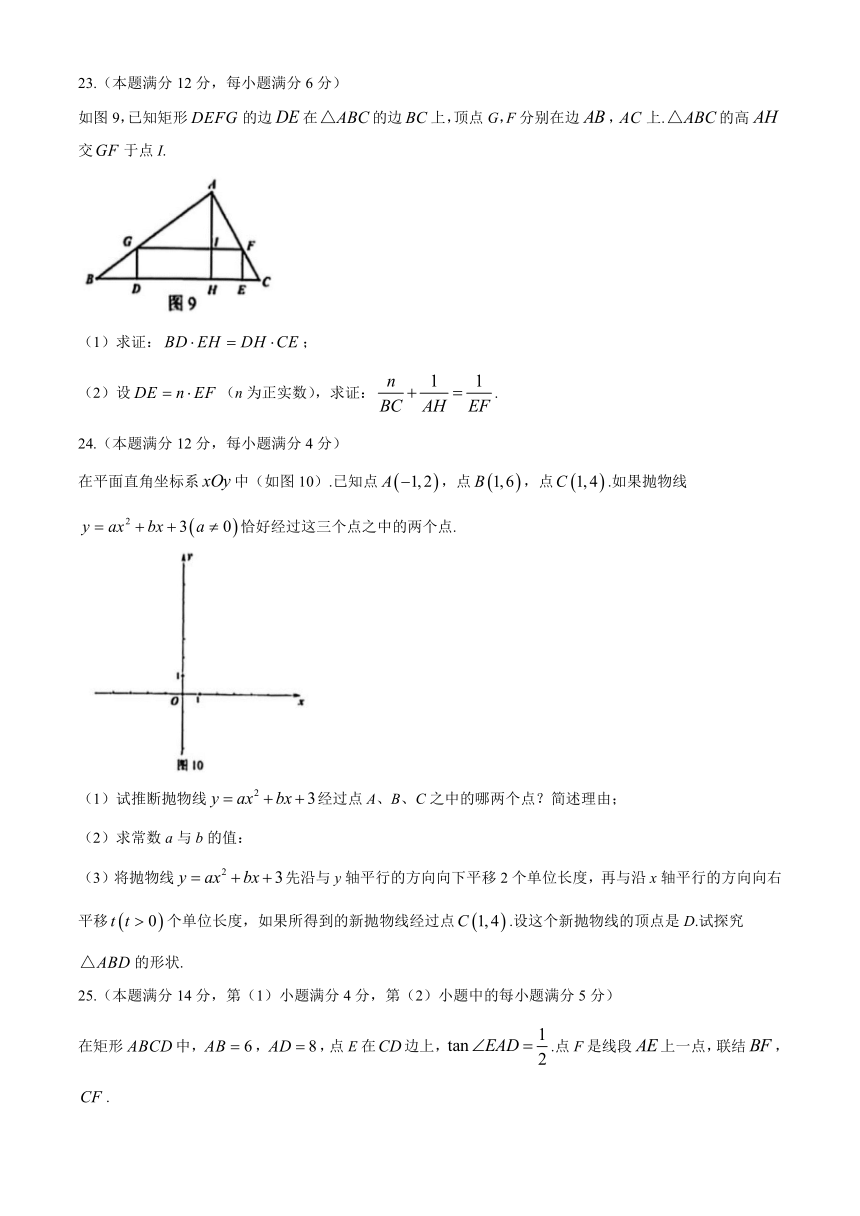
如图9,已知矩形的边在的边上,顶点G,F分别在边,上.的高交于点I.
(1)求证:;
(2)设(n为正实数),求证:.
24.(本题满分12分,每小题满分4分)
在平面直角坐标系中(如图10).已知点,点,点.如果抛物线恰好经过这三个点之中的两个点.
(1)试推断抛物线经过点A、B、C之中的哪两个点?简述理由;
(2)求常数a与b的值:
(3)将抛物线先沿与y轴平行的方向向下平移2个单位长度,再与沿x轴平行的方向向右平移个单位长度,如果所得到的新抛物线经过点.设这个新抛物线的顶点是D.试探究的形状.
25.(本题满分14分,第(1)小题满分4分,第(2)小题中的每小题满分5分)
在矩形中,,,点E在边上,.点F是线段上一点,联结,.
(1)如图11,如果,求线段的长;
(2)如图12,如果.
①求证:;
②求线段的长.
答案
1.考点:比例的性质
解析:注意题中的a、b、c、d是实数,在比例变化过程,需要分母不为零
答案:A
2.考点:锐角三角形
答案:D
3.考点:二次函数的顶点
答案:C
4.考点:单位向量
答案:B
5.考点:锐角三角形
答案:B
6.考点:二次函数的图像与性质
答案:A
7.考点:比例线段
答案:
8.考点:黄金分割点
答案:
9.考点:有公共边斜A型
答案:
10.考点:平面向量线性运算
答案:
11.考点:锐角三角边实际应用(俯角)
答案:60°
12.考点:锐角三角边实际应用(坡度)
答案:30°
13.考点:二次函数性质
答案:
14.考点:二次函数交点
答案:
15.考点:二次函数的顶点
答案:2
16.考点:二次函数对称轴
答案:二
17.考点:解三角形
答案:3
18.考点:旋转
解析:
如图: 如图,
答案:
19.考点:特殊角三角边的实数运算
原式
20.考点:二次函数的图像与性质,解二次函数
(1)对称轴:直线,最高点/顶点
开口方向:向下
当时,y随x增大而增大
当时,y随x增大而减小
(2)不可以,加上“”
设
代入得
∴
21.考点:X型,面积相关问题
(1)∵
∴
∴
∴
(2)∴,∴(共高△面积比等于底边之比)
∴
22.考点:解三角形
(1)作,垂足为点E.
∴,
∴
(2)作
∴
∴
23.考点:A型,三角形内接矩形
(1)
(2)
24.考点:解二次函数,函数图像平移
(1)∵轴,故B、C中只有一个点在抛物线上
∵,交y轴于点.
且抛物线与y轴也交于点,故C不符要求.
∴点A、B在抛物线上
(2)代入A、B到.
,
∴
(3)
∴
代入到,(舍),,
∴
∴,,
∴,,∴.
∴是等腰直角三角形
25.考点:解三角形
(1)解,∵
∴.作
设,,.
∴.∴,
(2)①在中:,,.
解,作,∵.
∴,.
∴.
∴
∴
②
数学试卷
(满分150分,考试时间100分钟)
同学们注意:
1.本试卷含三个大题,共25题;没有特殊说明,几何题均视为在同一个平面内研究问题.
2.答题时,务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效;
3.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.
一、选择题:(本大题共6题,每题4分,满分24分)
【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上.】
1.如果实数a,b,c,d满足,下列四个选项中,正确的是( )
A. B. C. D.
2.在平面直角坐标系中,已知点,点P与原点O的连线与x轴的正半轴的夹角为,那么的值是( )
A. B. C. D.3
3.抛物线的顶点坐标是( )
A. B. C. D.
4.已知单位向量与非零向量、,下列四个选项中,正确的是( )
A. B. C. D.
5.在中,,,,垂足为D.下列四个选项中,不正确的是( )
A. B. C. D.
6.二次函数的图像如图l所示,下列四个选项中,正确的是( )
A., B., C., D.,
二、填空题:(本大题共12题,每题4分,满分48分)
【请将结果直接填入答题纸的相应位置】
7.正方形的边长与它的对角线的长度的比值为______.
8.已知点P是线段的一个黄金分割点,且,那么的比值为______.
9.如图2,点D在的边上,当______时,与相似.
10.已知向量关系式,那么向量______.(用向量与向量表示)
11.如图3,飞机P在目标A的正上方,飞行员测得目标B的俯角为30°,那么的度数为______°.
12.如果一个斜坡的坡度,那么该斜坡的坡角的度数是______°.
13.如果抛物线的开口向下,那么实数a的取值范围是______.
14.二次函数的图像与y轴的交点坐标为______.
15.如果抛物线的顶点在x轴上,那么常数k为______.
16.如果抛物线的对称轴是直线,那么______0.(从<,=,>中选择)
17.如图4,正方形和正方形的边长相等,点A、B、C在同一条直线上.联结、,那么的值为______.
18.已知在中,,,(如图5),把绕着点C按顺时针方向旋转.将点A、B的对应点分别记为点、,如果为直角三角形,那么点A与点的距离为______.
三、解答题:(本大题共7题,满分78分)
19.(本题满分10分)
计算:
20.(本题满分10分,第(l)小题满分4分,第(2)小题满分6分)
我们已经知道二次函数的图像是一条抛物线.研究二次函数的图像与性质,我们主要关注抛物线的对称轴、抛物线的开口方向、抛物线的最高点(或最低点)的坐标、抛物线与坐标轴的交点坐标、抛物线的上升或下降情况(沿x轴的正方向看).
已知一个二次函数的大致图像如图6所示.
(1)你可以获得该二次函数的哪些信息?(写出四条信息即可)
(2)依据目前的信息,你可以求出这个二次函数的解析式吗?
如果可以,请求出这个二次函数的解析式;如果不可以,请补充一个条件,并求出这个二次函数的解析式.
21.(本题满分10分,每小题满分5分)
如图7,已知与相交于点O,联结.
(1)如果,,,求:.
(2)分别将、、记为、、,如果是与的比例中项,求证:.
22.(本题满分10分,每小题满分5分)
如图8,在中,,.
(1)求边的长度;
(2)求的值.
23.(本题满分12分,每小题满分6分)
如图9,已知矩形的边在的边上,顶点G,F分别在边,上.的高交于点I.
(1)求证:;
(2)设(n为正实数),求证:.
24.(本题满分12分,每小题满分4分)
在平面直角坐标系中(如图10).已知点,点,点.如果抛物线恰好经过这三个点之中的两个点.
(1)试推断抛物线经过点A、B、C之中的哪两个点?简述理由;
(2)求常数a与b的值:
(3)将抛物线先沿与y轴平行的方向向下平移2个单位长度,再与沿x轴平行的方向向右平移个单位长度,如果所得到的新抛物线经过点.设这个新抛物线的顶点是D.试探究的形状.
25.(本题满分14分,第(1)小题满分4分,第(2)小题中的每小题满分5分)
在矩形中,,,点E在边上,.点F是线段上一点,联结,.
(1)如图11,如果,求线段的长;
(2)如图12,如果.
①求证:;
②求线段的长.
答案
1.考点:比例的性质
解析:注意题中的a、b、c、d是实数,在比例变化过程,需要分母不为零
答案:A
2.考点:锐角三角形
答案:D
3.考点:二次函数的顶点
答案:C
4.考点:单位向量
答案:B
5.考点:锐角三角形
答案:B
6.考点:二次函数的图像与性质
答案:A
7.考点:比例线段
答案:
8.考点:黄金分割点
答案:
9.考点:有公共边斜A型
答案:
10.考点:平面向量线性运算
答案:
11.考点:锐角三角边实际应用(俯角)
答案:60°
12.考点:锐角三角边实际应用(坡度)
答案:30°
13.考点:二次函数性质
答案:
14.考点:二次函数交点
答案:
15.考点:二次函数的顶点
答案:2
16.考点:二次函数对称轴
答案:二
17.考点:解三角形
答案:3
18.考点:旋转
解析:
如图: 如图,
答案:
19.考点:特殊角三角边的实数运算
原式
20.考点:二次函数的图像与性质,解二次函数
(1)对称轴:直线,最高点/顶点
开口方向:向下
当时,y随x增大而增大
当时,y随x增大而减小
(2)不可以,加上“”
设
代入得
∴
21.考点:X型,面积相关问题
(1)∵
∴
∴
∴
(2)∴,∴(共高△面积比等于底边之比)
∴
22.考点:解三角形
(1)作,垂足为点E.
∴,
∴
(2)作
∴
∴
23.考点:A型,三角形内接矩形
(1)
(2)
24.考点:解二次函数,函数图像平移
(1)∵轴,故B、C中只有一个点在抛物线上
∵,交y轴于点.
且抛物线与y轴也交于点,故C不符要求.
∴点A、B在抛物线上
(2)代入A、B到.
,
∴
(3)
∴
代入到,(舍),,
∴
∴,,
∴,,∴.
∴是等腰直角三角形
25.考点:解三角形
(1)解,∵
∴.作
设,,.
∴.∴,
(2)①在中:,,.
解,作,∵.
∴,.
∴.
∴
∴
②
同课章节目录
