2020-2021学年山东省泰安市八年级(上)期末数学测试卷(五四学制)(word版含解析)
文档属性
| 名称 | 2020-2021学年山东省泰安市八年级(上)期末数学测试卷(五四学制)(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 160.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-15 21:59:26 | ||
图片预览



文档简介
2020-2021学年山东省泰安市八年级(上)期末数学测试卷(五四学制)
题号
一
二
三
总分
得分
第I卷(选择题)
一、选择题(本大题共12小题,共48.0分)
下列四个选项中,既是轴对称又是中心对称的图形是
A.
矩形
B.
等边三角形
C.
正五边形
D.
正七边形
根据分式的基本性质,分式可变形为
A.
B.
C.
D.
正多边形的一个外角的度数为,则这个正多边形的边数为
A.
4
B.
5
C.
6
D.
7
某学习小组的五名同学在一次数学竞赛中的成绩分别是94分、98分、90分、94分、74分,则下列结论正确的是
A.
平均分是91
B.
中位数是90
C.
众数是94
D.
极差是20
因式分解的正确结果是
A.
B.
C.
D.
在某次体育考试中,某校6名学生的体育成绩统计如图所示,则这组数据的中位数和方差分别是
A.
18,1
B.
17,3
C.
18,
D.
17,1
北京故宫博物院成立于1925年10月10日,是在明朝、清朝两代皇宫及其宫廷收藏的基础上建立起来的中国综合性博物馆,每年吸引着大批游客参观游览.下图是从2012年到2017年每年参观总人次的折线图.根据图中信息,下列结论中正确的是
A.
2012年以来,每年参观总人次逐年递增
B.
2014年比2013年增加的参观人次不超过50万
C.
2012年到2017年这六年间,2017年参观总人次最多
D.
2012年到2017年这六年间,平均每年参观总人次超过1600万
如图,绕点C顺时针旋转后得到,若,则的度数是
A.
B.
C.
D.
若分式方程无解,则a的值为?
???
A.
5
B.
4
C.
3
D.
0
如图,EF过?ABCD对角线的交点O,交AD于E,交BC于F,若?ABCD的周长为16,,则四边形EFCD的周长为
A.
10
B.
11
C.
12
D.
13
化简的结果是
A.
x
B.
C.
D.
如图,,,,点O为DF与GE的交点,图中共有平行四边形
A.
3个
B.
4个
C.
5个
D.
6个
第II卷(非选择题)
二、填空题(本大题共8小题,共32.0分)
若分式有意义,则x的取值范围是______
;当
______
时,分式的值为0.
分解因式:______.
当______时,关于x的分式方程有增根.
某水果店搞促销活动,对某种水果打8折出售.若用60元钱买这种水果,可以比打折前多买3千克.设该种水果打折前的单价为x元,根据题意可列方程为__________________.
如图,在平行四边形ABCD中,于点E,且,,,则______.
如图,是一个三角形,分别连接这个三角形三边中点得到图,再连接图中间小三角形三边的中点得到图,按这样的方法进行下去,第n个图形中共有三角形的个数为______.
如图,绕点A顺时针旋转得到,若,,则的度数是______
.
如图为,,其中,将AOB沿x轴依次以A,B,O为旋转中心顺时针旋转.分别得图,图,,则旋转到图时直角顶点的坐标是______.
三、解答题(本大题共7小题,共70.0分)
先化简,再求值:,其中.
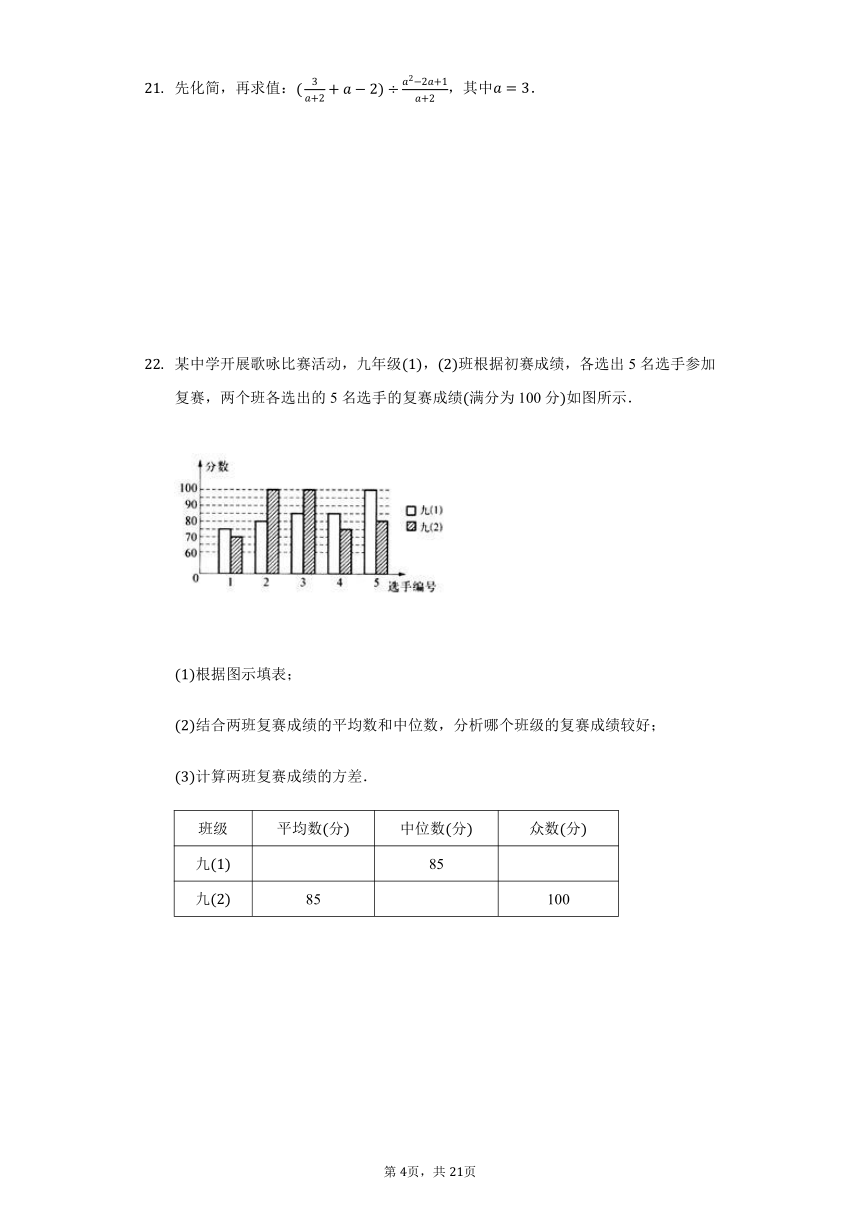
某中学开展歌咏比赛活动,九年级,班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩满分为100分如图所示.
根据图示填表;
结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
计算两班复赛成绩的方差.
班级
平均数分
中位数分
众数分
九
85
九
85
100
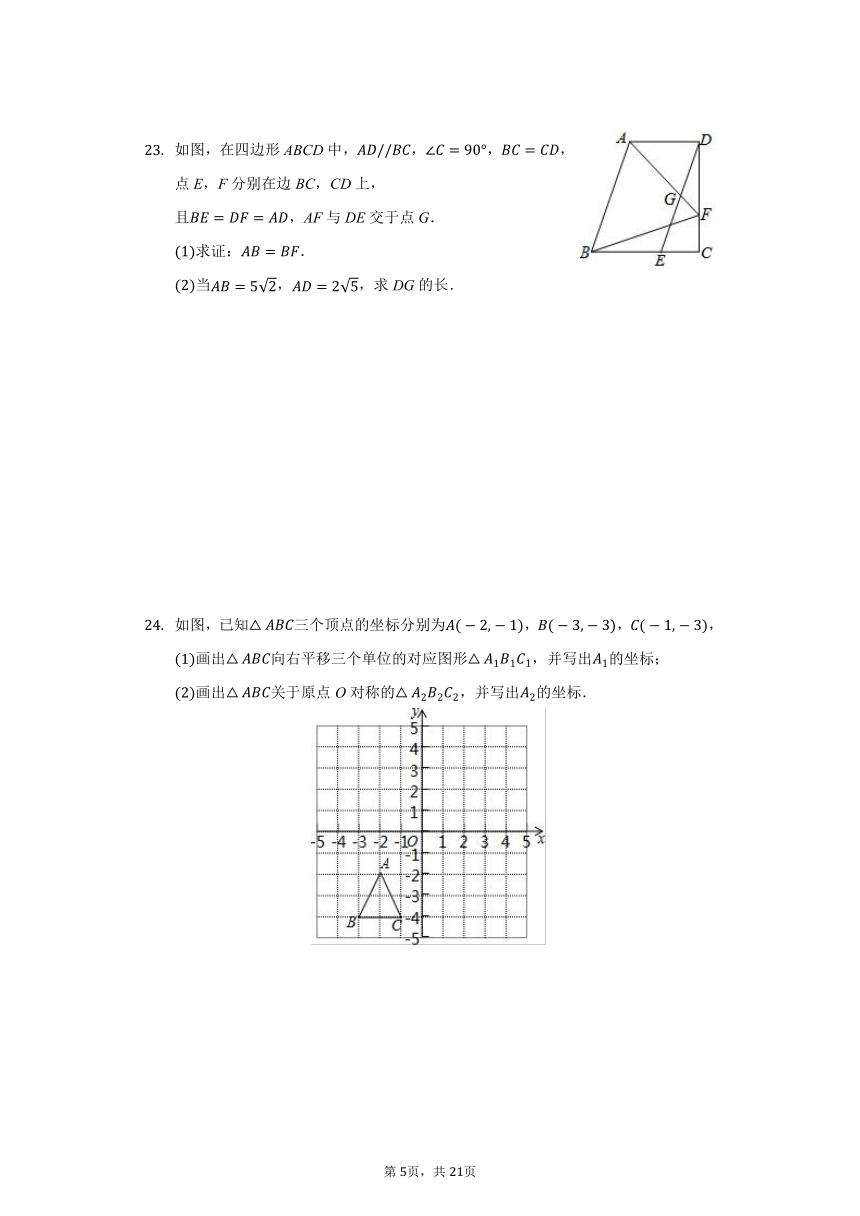
如图,在四边形ABCD中,,,,点E,F分别在边BC,CD上,
且,AF与DE交于点G.
求证:.
当,,求DG的长.
如图,已知三个顶点的坐标分别为,,,
画出向右平移三个单位的对应图形,并写出的坐标;
画出关于原点O对称的,并写出的坐标.
如图,将平行四边形纸片ABCD沿一条直线折叠,使点A与点C重合,点D落在点G处,折痕为求证:
;
≌.
六一前夕,某幼儿园园长到厂家选购A、B两种品牌的儿童服装,每套A品牌服装进价比B品牌服装每套进价多25元,用2000元购进A种服装数量是用750元购进B种服装数量的2倍.
求A、B两种品牌服装每套进价分别为多少元?
该服装A品牌每套售价为130元,B品牌每套售价为95元,服装店老板决定,购进B品牌服装的数量比购进A品牌服装的数量的2倍还多4套,两种服装全部售出后,可使总的获利超过1200元,则最少购进A品牌的服装多少套?
如图,D是等边三角形ABC内一点,将线段AD绕点A顺时针旋转,得到线段AE,连接CD,BE.
求证:;
连接DE,若,求的度数.
答案和解析
1.【答案】A
【解析】解:A、矩形是轴对称图形,也是中心对称图形,故此选项正确;
B、等边三角形是轴对称图形,不是中心对称图形,故此选项错误;
C、正五边形是轴对称图形,不是中心对称图形,故此选项错误;
D、正七边形是轴对称图形,不是中心对称图形,故此选项错误.
故选:A.
根据轴对称图形与中心对称图形的概念求解.
本题考查的是中心对称图形与轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后与原图重合.
2.【答案】A
【解析】
【分析】
此题考查了分式中的符号处理,注意同时改变其中两个符号,分式的值不变根据分式的基本性质,知分子、分母、分式本身的符号中,改变其中两个符号,分式的值不变.
【解答】解:同时改变了两个符号,分式的值不变,故本选项正确;
B.只改变了其中一个符号,分式的值改变,故本选项错误;
C.只改变了分子的符号,分式的值改变,故本选项错误;
D.改变了三个符号,分式的值改变,故本选项错误.
故选A.
3.【答案】B
【解析】解:正多边形的外角和是,
,那么它的边数是5.
故选:B.
正多边形的外角和是,这个正多边形的每个外角相等,因而用除以外角的度数,就得到外角和中外角的个数,外角的个数就是多边形的边数.
本题考查了多边形的内角与外角.根据正多边形的外角和求多边形的边数是常用的一种方法,需要熟记.
4.【答案】C
【解析】
【分析】
此题主要考查了平均数、中位数、众数以及极差的定义,正确把握相关定义是解题关键.直接利用平均数、中位数、众数以及极差的定义分别分析得出答案.
【解答】
解:平均分为:分,故A错误;
B.五名同学成绩按大小顺序排序为:74,90,94,94,98,故中位数是94,故B错误;
C.五名同学成绩按大小顺序排序为:74,90,94,94,98,故众数是94,故C正确;
D.极差是,故D错误.
故选C.
5.【答案】A
【解析】
【分析】
本题考查了提公因式法,公式法分解因式,提取公因式后利用平方差公式进行二次分解,注意分解要彻底.
先提取公因式y,再根据平方差公式进行二次分解即可求得答案.
【解答】
解:.
故选:A.
6.【答案】A
【解析】解:把这组数据从小到大排列,最中间两个数的平均数是,则中位数是18;
这组数据的平均数是:,
则方差是:.
故选:A.
根据中位数的定义和方差公式分别进行解答即可.
本题考查了中位数和方差,中位数是将一组数据从小到大或从大到小重新排列后,最中间的那个数或最中间两个数的平均数;一般地设n个数据,,,的平均数为,则方差
7.【答案】C
【解析】
【分析】本题考查折线统计图,解题的关键是读懂图象信息,属于中考常考题型.
观察折线图一一判断即可.
【解答】解:由从2012年到2017年每年参观人数的折线图,得:
在A中,2012年以来,2013年参观总人次比2012年参观人次少,故A错误;
在B中,2014年比2013年增加的参观人次超过50万,故B错误;
在C中,2012年到2017年这六年间,2017年参观总人次最多,故C正确;
在D中,2012年到2017年这六年间,平均每年参观总人次不超过1600万,故D错误.
故选C.
8.【答案】D
【解析】解:绕点C顺时针旋转后得到,
,
故选:D.
由旋转的性质,即可求解.
本题考查了旋转的性质,熟练运用旋转的性质是本题的关键.
9.【答案】A
【解析】
【分析】
本题考查了解分式方程,将分式方程去分母转化为整式方程,求得整式方程的解,然后由分式方程无解得到,求出a的值即可.
【解答】
解:去分母得:,
解得:,
分式方程无解,
,
,
故选A.
10.【答案】D
【解析】解:四边形ABCD是平行四边形,周长为16,
,,,,
,,
在和中,,
≌,
,,
则EFCD的周长.
故选:D.
先利用平行四边形的性质求出,,,可利用全等的性质得到≌,求出,即可求出四边形的周长.
本题考查了平行四边形的性质、全等三角形的判定与性质;熟练掌握平行四边形的性质,证明三角形全等是解决问题的关键.
11.【答案】B
【解析】解:原式
,
故选:B.
根据分式的运算法则即可求出答案.
本题考查分式的运算,解题的关键是熟练运用分式的运算法则,本题属于基础题型.
12.【答案】B
【解析】
【分析】
此题意在考查平行四边形的判定,根据题中给出的条件,依据两条对边分别平行的四边形为平行四边形,则不难求解.
本题主要考查了平行四边形的判定,熟练掌握平行四边形的性质及判定定理是解题的关键.
【解答】
解:因为,,,,
所以四边形GFDB,四边形GFCE,四边形EFGD,四边形AGOF均为平行四边形,
所以,共有四个平行四边形.
故选B.
13.【答案】;1
【解析】解:分式有意义,
.
解得:.
.
分式的值为0,
.
解得:.
故答案为:;1.
分式有意义的条件是分母不等于零;分式值为零的条件是分子等于零且分母不等于零.
本题主要考查的是分式值为零和分式有意义的条件,掌握分式值为零和分式有意义的条件是解题的关键.
14.【答案】
【解析】解:
.
故答案为:.
直接利用完全平方公式分解因式,进而利用平方差公式分解因式即可.
此题主要考查了提取公因式法以及公式法分解因式,正确应用公式是解题关键.
15.【答案】2
【解析】解:两边乘,得
,
解得,
由,得
.
解得,
故答案为:2.
增根是分式方程化为整式方程后产生的使分式方程的分母为0的根.把增根代入化为整式方程的方程即可求出m的值.
本题考查了分式方程的增根,增根确定后可按如下步骤进行:化分式方程为整式方程;把增根代入整式方程即可求得相关字母的值.
16.【答案】
【解析】
【分析】
本题考查分式方程的应用,正确理解题意,找出等量关系是解题的关键根据“若用60元钱买这种水果,可以比打折前多买3斤”为等量关系列出方程即可.
【解答】
解:设该种水果打折前的单价为x元,则打折后单价为元,根据题意可列方程为:
,
故答案为.
17.【答案】160
【解析】
【分析】
此题考查了平行四边形的性质以及勾股定理和三角形的面积的知识,注意利用面积求解是关键由BE::7,,可求得BE的长,然后利用勾股定理,求得AE的长,继而可求得?ABCD的面积.
【解答】
解:BE::7,,
,
,,
,
,
故答案为160.
18.【答案】
【解析】
【分析】
此题主要考查了图形的变化,解决此题的关键是寻找三角形的个数与图形的编号之间的关系.
结合题意,总结可知,每个图中三角形个数比图形的编号的4倍少3个三角形,即可得出结果.
【解答】
解:第是1个三角形,;
第是5个三角形,;
第是9个三角形,;
第n个图形中共有三角形的个数是.
故答案为.
19.【答案】
【解析】解:绕点A顺时针旋转得到,
,,
而,
,
.
故答案为:.
由绕点A顺时针旋转得到,根据旋转的性质得到,,再根据三角形的内角和定理得到,由此可得到的度数.
本题考查了旋转的性质:旋转前后的两个图形全等,对应点与旋转中心的连线的夹角定义旋转角;也考查了三角形的内角和定理.
20.【答案】
【解析】
【分析】
本题考查了坐标与图形的变化旋转,仔细观图形,判断出旋转规律“每3个图形为一个循环组依次循环,且下一组的第一个图形与上一组的最后一个图形的直角顶点重合”是解题的关键,根据勾股定理列式求出AB的长度,然后根据图形不难发现,每3个图形为一个循环组依次循环,且下一组的第一个图形与上一组的最后一个图形的直角顶点重合,所以,第10个图形的直角顶点与第9个图形的直角顶点重合,然后求解即可.
【解答】
解:,,,
,
根据图形,每3个图形为一个循环组,,
所以,图的直角顶点在x轴上,横坐标为,
所以,图的顶点坐标为,
又图的直角顶点与图的直角顶点重合,
图的直角顶点的坐标为.
故答案为:.
21.【答案】解:
,
当时,原式.
【解析】先算括号内加法,再把除法变成乘法,算乘法,最后代入求出即可.
本题考查了分式的混合运算和求值,能正确根据分式的运算法则进行化简是解此题的关键.
22.【答案】解:
班级
平均数分
中位数分
众数分
九
85
85
85
九
85
80
100
九班成绩好些.因为九班的中位数高,所以九班成绩好些.
,
.
【解析】
【分析】
本题考查了中位数、众数以及平均数的求法,同时也考查了方差公式,解题的关键是牢记定义并能熟练运用公式.
观察图分别写出九班和九班5名选手的复赛成绩,然后根据中位数的定义和平均数的求法以及众数的定义求解即可;
在平均数相同的情况下,中位数高的成绩较好;
根据方差公式计算即可:可简单记忆为“等于差方的平均数”【解答】
解:由图可知九班5名选手的复赛成绩为:75、80、85、85、100,
九班5名选手的复赛成绩为:70、100、100、75、80,
九班的平均数为,
九班的众数为85,
把九班的成绩按从小到大的顺序排列为:70、75、80、100、100,
九班的中位数是80;
故答案为
班级
平均数分
中位数分
众数分
九
85
85
85
九
85
80
100
见答案;
见答案.
23.【答案】解:证明:
,,
,
在与中,
≌,
,
,,
四边形ABED是平行四边形;
,
.
由可得,设,
在中,由勾股定理可得,
解得:,
延长AF交BC延长线于点H,
,
,
,
,
,
,
,
,
,
,
≌,
.
【解析】此题主要考查了平行四边形的判定与性质以及全等三角形的判定与性质等知识,根据已知得出≌是解题关键.
先证≌,再证四边形ABED是平行四边形,从而得;
延长AF交BC延长线于点H,设,在中,由勾股定理可得x的值,再根据全等证明点G是DE的中点即可求出DG的长.
24.【答案】解:如图所示:,即为所求;
?;
如图所示:,即为所求;.
【解析】直接利用平移的性质得出对应点位置进而得出答案;
直接利用旋转的性质分别得出对应点关于原点对称,进而得出答案.
此题主要考查了旋转变换以及平移变换,正确得出对应点位置是解题关键.
25.【答案】证明:
四边形ABCD是平行四边形,
,
由折叠可得,,
,
,
;
四边形ABCD是平行四边形,
,,
由折叠可得,,,
,,
又,
≌.
【解析】本题主要考查了平行四边形的性质,平行四边形的对边相等;平行四边形的对角相等;平行四边形的对角线互相平分.
依据平行四边形的性质,即可得到,由折叠可得,,即可得到;
依据平行四边形的性质,即可得出,,由折叠可得,,,即可得到,,进而得出≌.
26.【答案】解:设A品牌服装每套进价为x元,则B品牌服装每套进价为元,由题意得:
,
解得:,
经检验:是原分式方程的解,
,
答:A、B两种品牌服装每套进价分别为100元、75元;
设购进A品牌的服装a套,则购进B品牌服装套,由题意得:
,
解得:,
答:至少购进A品牌服装的数量是17套.
【解析】本题考查了分式方程的应用和一元一次不等式的应用,弄清题意,表示出A、B两种品牌服装每套进价,根据购进的服装的数量关系列出分式方程,求出进价是解决问题的关键.
首先设A品牌服装每套进价为x元,则B品牌服装每套进价为元,根据关键语句“用2000元购进A种服装数量是用750元购进B种服装数量的2倍.”列出方程,解方程即可,注意检验;
首先设购进A品牌的服装a套,则购进B品牌服装套,根据“可使总的获利超过1200元”可得不等式,再解不等式即可.
27.【答案】解:证明:等边三角形ABC,
,,
线段AD绕点A顺时针旋转,得到线段AE,
,,
,
,
≌,
;
,,
为等边三角形,
,
又,
.
【解析】本题考查了等边三角形的性质、旋转的性质以及全等三角形的判定和性质,熟练掌握旋转的性质证得三角形全等是解题的关键.
由等边三角形的性质知,,由旋转的性质知,,从而得,再证≌即可得到答案;
由,知为等边三角形,即,继而由可得的度数.
第2页,共2页
第1页,共1页
题号
一
二
三
总分
得分
第I卷(选择题)
一、选择题(本大题共12小题,共48.0分)
下列四个选项中,既是轴对称又是中心对称的图形是
A.
矩形
B.
等边三角形
C.
正五边形
D.
正七边形
根据分式的基本性质,分式可变形为
A.
B.
C.
D.
正多边形的一个外角的度数为,则这个正多边形的边数为
A.
4
B.
5
C.
6
D.
7
某学习小组的五名同学在一次数学竞赛中的成绩分别是94分、98分、90分、94分、74分,则下列结论正确的是
A.
平均分是91
B.
中位数是90
C.
众数是94
D.
极差是20
因式分解的正确结果是
A.
B.
C.
D.
在某次体育考试中,某校6名学生的体育成绩统计如图所示,则这组数据的中位数和方差分别是
A.
18,1
B.
17,3
C.
18,
D.
17,1
北京故宫博物院成立于1925年10月10日,是在明朝、清朝两代皇宫及其宫廷收藏的基础上建立起来的中国综合性博物馆,每年吸引着大批游客参观游览.下图是从2012年到2017年每年参观总人次的折线图.根据图中信息,下列结论中正确的是
A.
2012年以来,每年参观总人次逐年递增
B.
2014年比2013年增加的参观人次不超过50万
C.
2012年到2017年这六年间,2017年参观总人次最多
D.
2012年到2017年这六年间,平均每年参观总人次超过1600万
如图,绕点C顺时针旋转后得到,若,则的度数是
A.
B.
C.
D.
若分式方程无解,则a的值为?
???
A.
5
B.
4
C.
3
D.
0
如图,EF过?ABCD对角线的交点O,交AD于E,交BC于F,若?ABCD的周长为16,,则四边形EFCD的周长为
A.
10
B.
11
C.
12
D.
13
化简的结果是
A.
x
B.
C.
D.
如图,,,,点O为DF与GE的交点,图中共有平行四边形
A.
3个
B.
4个
C.
5个
D.
6个
第II卷(非选择题)
二、填空题(本大题共8小题,共32.0分)
若分式有意义,则x的取值范围是______
;当
______
时,分式的值为0.
分解因式:______.
当______时,关于x的分式方程有增根.
某水果店搞促销活动,对某种水果打8折出售.若用60元钱买这种水果,可以比打折前多买3千克.设该种水果打折前的单价为x元,根据题意可列方程为__________________.
如图,在平行四边形ABCD中,于点E,且,,,则______.
如图,是一个三角形,分别连接这个三角形三边中点得到图,再连接图中间小三角形三边的中点得到图,按这样的方法进行下去,第n个图形中共有三角形的个数为______.
如图,绕点A顺时针旋转得到,若,,则的度数是______
.
如图为,,其中,将AOB沿x轴依次以A,B,O为旋转中心顺时针旋转.分别得图,图,,则旋转到图时直角顶点的坐标是______.
三、解答题(本大题共7小题,共70.0分)
先化简,再求值:,其中.
某中学开展歌咏比赛活动,九年级,班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩满分为100分如图所示.
根据图示填表;
结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
计算两班复赛成绩的方差.
班级
平均数分
中位数分
众数分
九
85
九
85
100
如图,在四边形ABCD中,,,,点E,F分别在边BC,CD上,
且,AF与DE交于点G.
求证:.
当,,求DG的长.
如图,已知三个顶点的坐标分别为,,,
画出向右平移三个单位的对应图形,并写出的坐标;
画出关于原点O对称的,并写出的坐标.
如图,将平行四边形纸片ABCD沿一条直线折叠,使点A与点C重合,点D落在点G处,折痕为求证:
;
≌.
六一前夕,某幼儿园园长到厂家选购A、B两种品牌的儿童服装,每套A品牌服装进价比B品牌服装每套进价多25元,用2000元购进A种服装数量是用750元购进B种服装数量的2倍.
求A、B两种品牌服装每套进价分别为多少元?
该服装A品牌每套售价为130元,B品牌每套售价为95元,服装店老板决定,购进B品牌服装的数量比购进A品牌服装的数量的2倍还多4套,两种服装全部售出后,可使总的获利超过1200元,则最少购进A品牌的服装多少套?
如图,D是等边三角形ABC内一点,将线段AD绕点A顺时针旋转,得到线段AE,连接CD,BE.
求证:;
连接DE,若,求的度数.
答案和解析
1.【答案】A
【解析】解:A、矩形是轴对称图形,也是中心对称图形,故此选项正确;
B、等边三角形是轴对称图形,不是中心对称图形,故此选项错误;
C、正五边形是轴对称图形,不是中心对称图形,故此选项错误;
D、正七边形是轴对称图形,不是中心对称图形,故此选项错误.
故选:A.
根据轴对称图形与中心对称图形的概念求解.
本题考查的是中心对称图形与轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后与原图重合.
2.【答案】A
【解析】
【分析】
此题考查了分式中的符号处理,注意同时改变其中两个符号,分式的值不变根据分式的基本性质,知分子、分母、分式本身的符号中,改变其中两个符号,分式的值不变.
【解答】解:同时改变了两个符号,分式的值不变,故本选项正确;
B.只改变了其中一个符号,分式的值改变,故本选项错误;
C.只改变了分子的符号,分式的值改变,故本选项错误;
D.改变了三个符号,分式的值改变,故本选项错误.
故选A.
3.【答案】B
【解析】解:正多边形的外角和是,
,那么它的边数是5.
故选:B.
正多边形的外角和是,这个正多边形的每个外角相等,因而用除以外角的度数,就得到外角和中外角的个数,外角的个数就是多边形的边数.
本题考查了多边形的内角与外角.根据正多边形的外角和求多边形的边数是常用的一种方法,需要熟记.
4.【答案】C
【解析】
【分析】
此题主要考查了平均数、中位数、众数以及极差的定义,正确把握相关定义是解题关键.直接利用平均数、中位数、众数以及极差的定义分别分析得出答案.
【解答】
解:平均分为:分,故A错误;
B.五名同学成绩按大小顺序排序为:74,90,94,94,98,故中位数是94,故B错误;
C.五名同学成绩按大小顺序排序为:74,90,94,94,98,故众数是94,故C正确;
D.极差是,故D错误.
故选C.
5.【答案】A
【解析】
【分析】
本题考查了提公因式法,公式法分解因式,提取公因式后利用平方差公式进行二次分解,注意分解要彻底.
先提取公因式y,再根据平方差公式进行二次分解即可求得答案.
【解答】
解:.
故选:A.
6.【答案】A
【解析】解:把这组数据从小到大排列,最中间两个数的平均数是,则中位数是18;
这组数据的平均数是:,
则方差是:.
故选:A.
根据中位数的定义和方差公式分别进行解答即可.
本题考查了中位数和方差,中位数是将一组数据从小到大或从大到小重新排列后,最中间的那个数或最中间两个数的平均数;一般地设n个数据,,,的平均数为,则方差
7.【答案】C
【解析】
【分析】本题考查折线统计图,解题的关键是读懂图象信息,属于中考常考题型.
观察折线图一一判断即可.
【解答】解:由从2012年到2017年每年参观人数的折线图,得:
在A中,2012年以来,2013年参观总人次比2012年参观人次少,故A错误;
在B中,2014年比2013年增加的参观人次超过50万,故B错误;
在C中,2012年到2017年这六年间,2017年参观总人次最多,故C正确;
在D中,2012年到2017年这六年间,平均每年参观总人次不超过1600万,故D错误.
故选C.
8.【答案】D
【解析】解:绕点C顺时针旋转后得到,
,
故选:D.
由旋转的性质,即可求解.
本题考查了旋转的性质,熟练运用旋转的性质是本题的关键.
9.【答案】A
【解析】
【分析】
本题考查了解分式方程,将分式方程去分母转化为整式方程,求得整式方程的解,然后由分式方程无解得到,求出a的值即可.
【解答】
解:去分母得:,
解得:,
分式方程无解,
,
,
故选A.
10.【答案】D
【解析】解:四边形ABCD是平行四边形,周长为16,
,,,,
,,
在和中,,
≌,
,,
则EFCD的周长.
故选:D.
先利用平行四边形的性质求出,,,可利用全等的性质得到≌,求出,即可求出四边形的周长.
本题考查了平行四边形的性质、全等三角形的判定与性质;熟练掌握平行四边形的性质,证明三角形全等是解决问题的关键.
11.【答案】B
【解析】解:原式
,
故选:B.
根据分式的运算法则即可求出答案.
本题考查分式的运算,解题的关键是熟练运用分式的运算法则,本题属于基础题型.
12.【答案】B
【解析】
【分析】
此题意在考查平行四边形的判定,根据题中给出的条件,依据两条对边分别平行的四边形为平行四边形,则不难求解.
本题主要考查了平行四边形的判定,熟练掌握平行四边形的性质及判定定理是解题的关键.
【解答】
解:因为,,,,
所以四边形GFDB,四边形GFCE,四边形EFGD,四边形AGOF均为平行四边形,
所以,共有四个平行四边形.
故选B.
13.【答案】;1
【解析】解:分式有意义,
.
解得:.
.
分式的值为0,
.
解得:.
故答案为:;1.
分式有意义的条件是分母不等于零;分式值为零的条件是分子等于零且分母不等于零.
本题主要考查的是分式值为零和分式有意义的条件,掌握分式值为零和分式有意义的条件是解题的关键.
14.【答案】
【解析】解:
.
故答案为:.
直接利用完全平方公式分解因式,进而利用平方差公式分解因式即可.
此题主要考查了提取公因式法以及公式法分解因式,正确应用公式是解题关键.
15.【答案】2
【解析】解:两边乘,得
,
解得,
由,得
.
解得,
故答案为:2.
增根是分式方程化为整式方程后产生的使分式方程的分母为0的根.把增根代入化为整式方程的方程即可求出m的值.
本题考查了分式方程的增根,增根确定后可按如下步骤进行:化分式方程为整式方程;把增根代入整式方程即可求得相关字母的值.
16.【答案】
【解析】
【分析】
本题考查分式方程的应用,正确理解题意,找出等量关系是解题的关键根据“若用60元钱买这种水果,可以比打折前多买3斤”为等量关系列出方程即可.
【解答】
解:设该种水果打折前的单价为x元,则打折后单价为元,根据题意可列方程为:
,
故答案为.
17.【答案】160
【解析】
【分析】
此题考查了平行四边形的性质以及勾股定理和三角形的面积的知识,注意利用面积求解是关键由BE::7,,可求得BE的长,然后利用勾股定理,求得AE的长,继而可求得?ABCD的面积.
【解答】
解:BE::7,,
,
,,
,
,
故答案为160.
18.【答案】
【解析】
【分析】
此题主要考查了图形的变化,解决此题的关键是寻找三角形的个数与图形的编号之间的关系.
结合题意,总结可知,每个图中三角形个数比图形的编号的4倍少3个三角形,即可得出结果.
【解答】
解:第是1个三角形,;
第是5个三角形,;
第是9个三角形,;
第n个图形中共有三角形的个数是.
故答案为.
19.【答案】
【解析】解:绕点A顺时针旋转得到,
,,
而,
,
.
故答案为:.
由绕点A顺时针旋转得到,根据旋转的性质得到,,再根据三角形的内角和定理得到,由此可得到的度数.
本题考查了旋转的性质:旋转前后的两个图形全等,对应点与旋转中心的连线的夹角定义旋转角;也考查了三角形的内角和定理.
20.【答案】
【解析】
【分析】
本题考查了坐标与图形的变化旋转,仔细观图形,判断出旋转规律“每3个图形为一个循环组依次循环,且下一组的第一个图形与上一组的最后一个图形的直角顶点重合”是解题的关键,根据勾股定理列式求出AB的长度,然后根据图形不难发现,每3个图形为一个循环组依次循环,且下一组的第一个图形与上一组的最后一个图形的直角顶点重合,所以,第10个图形的直角顶点与第9个图形的直角顶点重合,然后求解即可.
【解答】
解:,,,
,
根据图形,每3个图形为一个循环组,,
所以,图的直角顶点在x轴上,横坐标为,
所以,图的顶点坐标为,
又图的直角顶点与图的直角顶点重合,
图的直角顶点的坐标为.
故答案为:.
21.【答案】解:
,
当时,原式.
【解析】先算括号内加法,再把除法变成乘法,算乘法,最后代入求出即可.
本题考查了分式的混合运算和求值,能正确根据分式的运算法则进行化简是解此题的关键.
22.【答案】解:
班级
平均数分
中位数分
众数分
九
85
85
85
九
85
80
100
九班成绩好些.因为九班的中位数高,所以九班成绩好些.
,
.
【解析】
【分析】
本题考查了中位数、众数以及平均数的求法,同时也考查了方差公式,解题的关键是牢记定义并能熟练运用公式.
观察图分别写出九班和九班5名选手的复赛成绩,然后根据中位数的定义和平均数的求法以及众数的定义求解即可;
在平均数相同的情况下,中位数高的成绩较好;
根据方差公式计算即可:可简单记忆为“等于差方的平均数”【解答】
解:由图可知九班5名选手的复赛成绩为:75、80、85、85、100,
九班5名选手的复赛成绩为:70、100、100、75、80,
九班的平均数为,
九班的众数为85,
把九班的成绩按从小到大的顺序排列为:70、75、80、100、100,
九班的中位数是80;
故答案为
班级
平均数分
中位数分
众数分
九
85
85
85
九
85
80
100
见答案;
见答案.
23.【答案】解:证明:
,,
,
在与中,
≌,
,
,,
四边形ABED是平行四边形;
,
.
由可得,设,
在中,由勾股定理可得,
解得:,
延长AF交BC延长线于点H,
,
,
,
,
,
,
,
,
,
,
≌,
.
【解析】此题主要考查了平行四边形的判定与性质以及全等三角形的判定与性质等知识,根据已知得出≌是解题关键.
先证≌,再证四边形ABED是平行四边形,从而得;
延长AF交BC延长线于点H,设,在中,由勾股定理可得x的值,再根据全等证明点G是DE的中点即可求出DG的长.
24.【答案】解:如图所示:,即为所求;
?;
如图所示:,即为所求;.
【解析】直接利用平移的性质得出对应点位置进而得出答案;
直接利用旋转的性质分别得出对应点关于原点对称,进而得出答案.
此题主要考查了旋转变换以及平移变换,正确得出对应点位置是解题关键.
25.【答案】证明:
四边形ABCD是平行四边形,
,
由折叠可得,,
,
,
;
四边形ABCD是平行四边形,
,,
由折叠可得,,,
,,
又,
≌.
【解析】本题主要考查了平行四边形的性质,平行四边形的对边相等;平行四边形的对角相等;平行四边形的对角线互相平分.
依据平行四边形的性质,即可得到,由折叠可得,,即可得到;
依据平行四边形的性质,即可得出,,由折叠可得,,,即可得到,,进而得出≌.
26.【答案】解:设A品牌服装每套进价为x元,则B品牌服装每套进价为元,由题意得:
,
解得:,
经检验:是原分式方程的解,
,
答:A、B两种品牌服装每套进价分别为100元、75元;
设购进A品牌的服装a套,则购进B品牌服装套,由题意得:
,
解得:,
答:至少购进A品牌服装的数量是17套.
【解析】本题考查了分式方程的应用和一元一次不等式的应用,弄清题意,表示出A、B两种品牌服装每套进价,根据购进的服装的数量关系列出分式方程,求出进价是解决问题的关键.
首先设A品牌服装每套进价为x元,则B品牌服装每套进价为元,根据关键语句“用2000元购进A种服装数量是用750元购进B种服装数量的2倍.”列出方程,解方程即可,注意检验;
首先设购进A品牌的服装a套,则购进B品牌服装套,根据“可使总的获利超过1200元”可得不等式,再解不等式即可.
27.【答案】解:证明:等边三角形ABC,
,,
线段AD绕点A顺时针旋转,得到线段AE,
,,
,
,
≌,
;
,,
为等边三角形,
,
又,
.
【解析】本题考查了等边三角形的性质、旋转的性质以及全等三角形的判定和性质,熟练掌握旋转的性质证得三角形全等是解题的关键.
由等边三角形的性质知,,由旋转的性质知,,从而得,再证≌即可得到答案;
由,知为等边三角形,即,继而由可得的度数.
第2页,共2页
第1页,共1页
同课章节目录
