江西省赣县第三中学2020-2021学年高二上学期期末复习理科数学试卷Word含解析
文档属性
| 名称 | 江西省赣县第三中学2020-2021学年高二上学期期末复习理科数学试卷Word含解析 |  | |
| 格式 | doc | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-17 21:29:04 | ||
图片预览




文档简介
高二理复习卷数学
命题人: 审题人: 2021年1月9日
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.设P是双曲线=1(a>0,b>0)上的点,F1?F2是焦点,双曲线的离心率是,且∠F1PF2=90°,△F1PF2的面积是7,则a+b等于( )
A.3+ B.9+ C.10 D.16
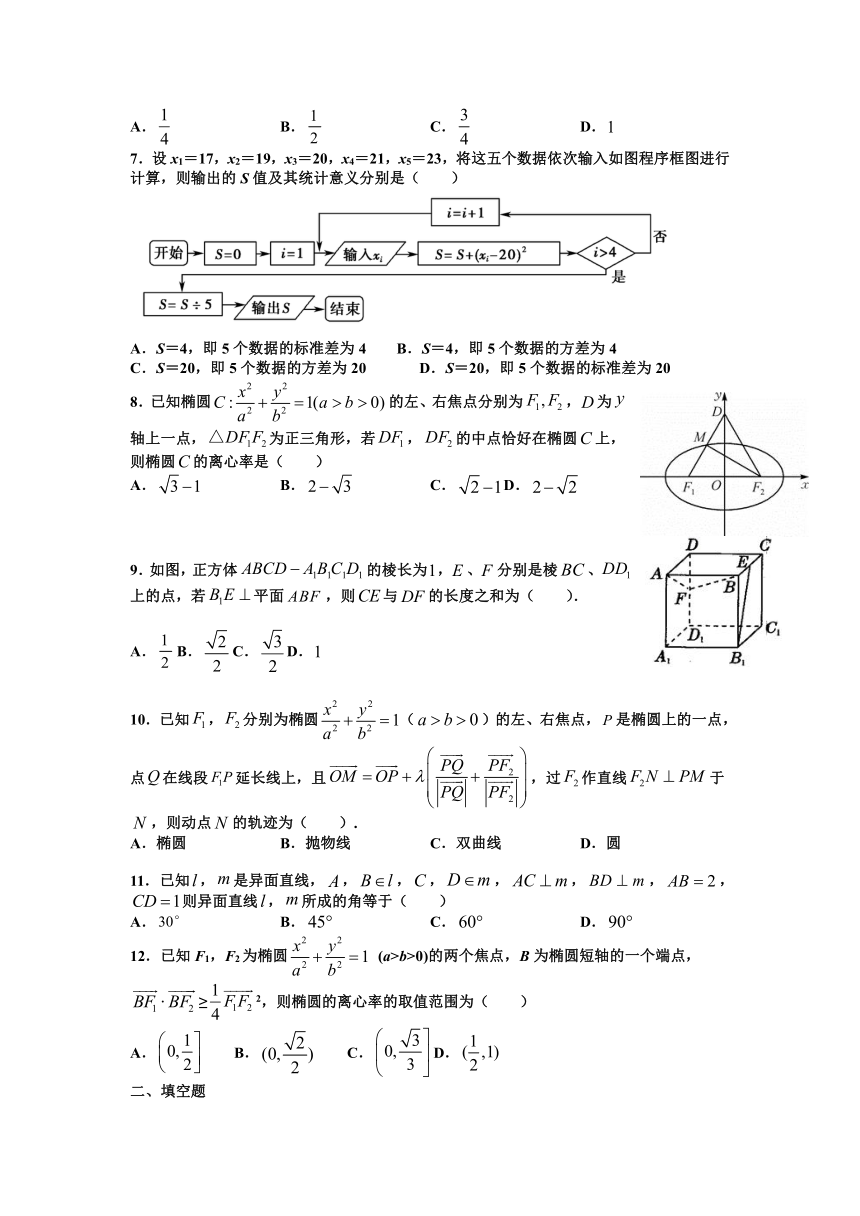
2.为了保证抗击新型冠状肺炎期间的蔬菜供应,某大型超市统计了2月1号~10号连续天蔬菜进货量和出货量(单位:吨)如图所示,则下列说法错误的是( )
A.出货量的最高值与出货量的最低值的比是
B.天中剩余蔬菜最多的一天是2月4号
C.2月3号~4号的进货量的变化率比2月7号~8号进货量的变化率大
D.这10天每天平均剩余蔬菜为21吨
3.已知命题:且,都有;命题:,.则下列命题中为真命题的是( )
A. B. C. D.
4.如图,边长为的正方形中,点、分别是、的中点,将、、分别沿、、折起,使得、、三点重合于点,若四面体的四个顶点在同一个球面上,则该球的表面积为( ).
A.B.C.D.
5.新冠肺炎肆虐全,疫情波及多个国家和地区;一些国家宣布进入“紧急状态”,全球股市剧烈震荡……新冠肺炎疫情严重挑战公共卫生安全,全面冲击世界经济运行,深刻影响社会生活运转.这场全球公共卫生危机,需要国际社会的通力合作,在一次国际医学学术会议上,来自四个国家的五位代表被安排在一张圆桌就座,为了使他们能够自由交谈,事先了解到的情况如下:甲是中国人,还会说英语;乙是法国人,还会说日语;丙是英国人,还会说法语;丁是日本人,还会说汉语;戊是法国人,还会说德语;则这五位代表的座位顺序应为( )
A.甲丙丁戊乙 B.甲丁丙乙戊
C.甲乙丙丁戊 D.甲丙戊乙丁
6.设是正三棱锥,是的重心,是上的一点,且,若,则( ).
A. B. C. D.
7.设x1=17,x2=19,x3=20,x4=21,x5=23,将这五个数据依次输入如图程序框图进行计算,则输出的S值及其统计意义分别是( )
A.S=4,即5个数据的标准差为4 B.S=4,即5个数据的方差为4
C.S=20,即5个数据的方差为20 D.S=20,即5个数据的标准差为20
8.已知椭圆的左、右焦点分别为,为轴上一点,为正三角形,若,的中点恰好在椭圆上,则椭圆的离心率是( )
A. B. C.D.
9.如图,正方体的棱长为,、分别是棱、上的点,若平面,则与的长度之和为( ).
A.B.C.D.
10.已知,分别为椭圆()的左、右焦点,是椭圆上的一点,点在线段延长线上,且,过作直线于,则动点的轨迹为( ).
A.椭圆 B.抛物线 C.双曲线 D.圆
11.已知,是异面直线,,,,,,,,则异面直线,所成的角等于( )
A. B. C. D.
12.已知F1,F2为椭圆 (a>b>0)的两个焦点,B为椭圆短轴的一个端点,·≥2,则椭圆的离心率的取值范围为( )
A. B. C. D.
二、填空题
13.若“存在x∈[﹣1,1],成立”为真命题,则a的取值范围是___.
14.甲、乙两人下棋,两人下成和棋的概率是,甲获胜的概率是,则乙获胜的概率是_________.
15.长方体中,,设点关于直线对称点为,则点与点之间的距离是_________
16.对抛物线:,有下列命题:
①设直线:,则直线被抛物线所截得的最短弦长为4;
②已知直线:交抛物线于、两点,则以为直径的圆一定与抛物线的准线相切;
③过点与抛物线有且只有一个交点的直线有1条或3条;
④若抛物线的焦点为,抛物线上一点和抛物线内一点,过点作抛物线的切线,直线过点且与垂直,则平分;
其中你认为是正确命题的所有命题的序号是______.
三、解答题
17.已知某中学高三文科班学生共有800人参加了数学与地理的水平测试,现学校决定利用随机数表法从中抽取100人进行成绩统计,先将800人按001,002,003,…,800进行编号.
(1)如果从随机数表的第8行第7列的数开始向右读,请你依次写出最先抽取到的3个人的编号.
(2)所抽取的100人的数学与地理的水平测试成绩如下表:
人数 数学
优秀 良好 及格
地理 优秀 7 20 5
良好 9 18 6
及格 a 4 b
成绩分为优秀、良好、及格三个等级,横向、纵向分别表示地理成绩与数学成绩,例如表中数学成绩为良好的人数为20+18+4=42.若在该样本中,数学成绩优秀率为30%,求,的值.
(3)若,,求“在地理成绩为及格的学生中,数学成绩为优秀的人数比及格的人数少”的概率.
附:(下面摘取了随机数表的第7行至第9行)
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67
21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 55 67 19 98 10 50 71 75
12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38
15 51 00 13 42 99 66 02 79 54
18.从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于和之间,将测量结果按如下方式分成八组:第一组,第二组,…,第八组,下图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人.
(1)求第七组的频率并估计该校800名男生中身高在以上(含)的人数;
(2)估计该校800名男生的身高中位数和平均数;
(3)从第六组和第八组的男生中随机抽取两名男生,记他们的身高分别为,,事件,求.
19.设命题实数满足;命题实数满足
(1)若,,都是真命题,求实数的取值范围;
(2)若是的充分不必要条件,求实数的取值范围.
20.如图,在四棱锥 P-ABCD中,△PAB为正三角形,四边形ABCD为矩形,且平面PAB⊥平面ABCD,AB=2,PC=4
(1)求证:平面PAB⊥平面PAD
(2)在线段PA上是否存在一点N,使得二面角A-BD-N的余弦值为若存在,求出点N的位置;若不存在,请说明理由
21.(1)用分析法证明:当,时,;
(2)证明:对任意,,,这个值至少有一个不小于.
22.抛物线与直线有唯一公共点,且的焦点为.
(1)用含的式子表示.
(2)若点与关于直线对称,证明的纵坐标为定值.
23.如图,在三棱柱中,已知是直角三角形,侧面是矩形,AB=BC=1,BB1=2,.
(1)证明:BC1⊥AC.
(2)E是棱CC1的中点,求直线B1C与平面ABE所成角的正弦值.
24.已知椭圆的中心在坐标原点,焦点在轴上,离心率为,右焦点到右顶点的距离为1.
(1)求椭圆的标准方程.
(2)是否存在与椭圆交于,两点的直线:,使得成立?若存在,求出实数的取值范围;若不存在,请说明理由.
(3)若动直线与椭圆有且仅有一个公共点,试问:在轴上是否存在两定点,使其到直线的距离之积为3?若存在,求出两定点坐标;若不存在,请说明理由.
高二理复习卷数学
命题人: 审题人: 2021年1月9日
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.设P是双曲线=1(a>0,b>0)上的点,F1?F2是焦点,双曲线的离心率是,且∠F1PF2=90°,△F1PF2的面积是7,则a+b等于( )
A.3+ B.9+ C.10 D.16
由题意,不妨设点P是右支上的一点,|PF1|=m,|PF2|=n,则∴a=3,c=4.
∴b=.∴a+b=3+.故选:A
2.为了保证抗击新型冠状肺炎期间的蔬菜供应,某大型超市统计了2月1号~10号连续天蔬菜进货量和出货量(单位:吨)如图所示,则下列说法错误的是( )
A.出货量的最高值与出货量的最低值的比是
B.天中剩余蔬菜最多的一天是2月4号
C.2月3号~4号的进货量的变化率比2月7号~8号进货量的变化率大
D.这10天每天平均剩余蔬菜为21吨
【答案】A根据给定的2月1号~10号连续天蔬菜进货量和出货量(单位:吨)统计图表,
可得:出货量的最高值与出货量的最低值的比应是,所以A错误;
这天中,从每天的剩余吨数为:,其中2月4号剩余蔬菜量为吨,这是中,剩余蔬菜最多的一天,所以B正确;
2月3号~4号进货量的变化率为,2月7号~8号进货量变化率为,
所以2月3号~4号的进货量的变化率比2月7号~8号进货量的变化率大,所以C正确;
由,即这10天每天平均剩余蔬菜为21吨,所以D正确.
3.已知命题:且,都有;命题:,.则下列命题中为真命题的是( )
A. B. C. D.
当时,,所以命题是假命题,
因为恒成立,所以命题:,为假命题.
所以为真命题.故选:D
4.如图,边长为的正方形中,点、分别是、的中点,将、、分别沿、、折起,使得、、三点重合于点,若四面体的四个顶点在同一个球面上,则该球的表面积为( ).
A.B.C.D.
四面体为底面为等腰,顶点为的三棱锥,
则,,,,则,,
又,则为直角三角形,,
以为原点建立如图所示的空间直角坐标系,
则,,,,
设四面体的外接球的球心为,则,由空间两点间距离公式知:,,
,解得,,,
所以半径为,
所以该球的表面积为.
5.新冠肺炎肆虐全,疫情波及多个国家和地区;一些国家宣布进入“紧急状态”,全球股市剧烈震荡……新冠肺炎疫情严重挑战公共卫生安全,全面冲击世界经济运行,深刻影响社会生活运转.这场全球公共卫生危机,需要国际社会的通力合作,在一次国际医学学术会议上,来自四个国家的五位代表被安排在一张圆桌就座,为了使他们能够自由交谈,事先了解到的情况如下:甲是中国人,还会说英语;乙是法国人,还会说日语;丙是英国人,还会说法语;丁是日本人,还会说汉语;戊是法国人,还会说德语;则这五位代表的座位顺序应为( )
A.甲丙丁戊乙 B.甲丁丙乙戊
C.甲乙丙丁戊 D.甲丙戊乙丁
【答案】D
戊是法国人,还会说德语,只能用法语交流,则两侧只能是乙和丙,乙旁边是丁,丙旁边是甲,
6.设是正三棱锥,是的重心,是上的一点,且,若,则( ).
A. B. C. D.
如下图所示,连接并延长交于点,则点为的中点,
为的重心,可得,
而,
,
所以,,
所以,,因此,.
7.设x1=17,x2=19,x3=20,x4=21,x5=23,将这五个数据依次输入如图程序框图进行计算,则输出的S值及其统计意义分别是( )
A.S=4,即5个数据的标准差为4 B.S=4,即5个数据的方差为4
C.S=20,即5个数据的方差为20 D.S=20,即5个数据的标准差为20
数据,则,
根据程序框图进行计算,则输出
,它是计算这5个数据的方差.故选:B.
8.已知椭圆的左、右焦点分别为,为轴上一点,为正三角形,若,的中点恰好在椭圆上,则椭圆的离心率是( )
A. B. C.D.
因为为正三角形,所以,取线段的中点,连结,则,所以,得,所以椭圆的离心率.故选:A.
9.如图,正方体的棱长为,、分别是棱、上的点,若平面,则与的长度之和为( ).
A.B.C.D.
以为坐标原点,、、为、、轴建立空间直角坐标系,设,,
则,,,,
∴,,由于平面,
∴,即, 故与的长度之和为.故选:D.
10.已知,分别为椭圆()的左、右焦点,是椭圆上的一点,点在线段延长线上,且,过作直线于,则动点的轨迹为( ).
A.椭圆 B.抛物线 C.双曲线 D.圆
根据题意,即
故平分,又因为,设关于的对称点为,所以,
由椭圆定义可得,在中,为中位线,
故,所以(定值),故点的轨迹为圆.
11.已知,是异面直线,,,,,,,,则异面直线,所成的角等于( )
A. B. C. D.
【答案】C
,因为,故,所以,
而,故,所以,整理得到:,因为,故,故异面直线,所成的角为.
12.已知F1,F2为椭圆 (a>b>0)的两个焦点,B为椭圆短轴的一个端点,·≥2,则椭圆的离心率的取值范围为( )
A. B. C. D.
根据题意不妨设B(0,b),F1(-c,0),F2(c,0),
因为,所以,又因为b2=a2-c2,所以,即..故选:C.
二、填空题
13.若“存在x∈[﹣1,1],成立”为真命题,则a的取值范围是___.
【答案】
存在x∈[﹣1,1],成立,即在上有解,
设,,易得y=f(x)在[﹣1,1]为减函数,
所以,即,即,
即,所以,故答案为:.
14.甲、乙两人下棋,两人下成和棋的概率是,甲获胜的概率是,则乙获胜的概率是_________.
【答案】。因为事件“乙获胜”与事件“两人下和棋或甲获胜”互为对立事件,所以乙获胜的概率.故答案为:
15.长方体中,,设点关于直线对称点为,则点与点之间的距离是_________
【答案】
画出过点,线段的平面图如图所示:过点作于点,
因为点是点关于直线对称点,所以且平分,
所以,
因为长方体中,,
所以,,,
所以,,所以
,,在中由余弦定理得
,
16.对抛物线:,有下列命题:
①设直线:,则直线被抛物线所截得的最短弦长为4;
②已知直线:交抛物线于、两点,则以为直径的圆一定与抛物线的准线相切;
③过点与抛物线有且只有一个交点的直线有1条或3条;
④若抛物线的焦点为,抛物线上一点和抛物线内一点,过点作抛物线的切线,直线过点且与垂直,则平分;
其中你认为是正确命题的所有命题的序号是______.
【答案】①②④
①联立方程,消去可得,恒成立,
设两交点坐标分别为,,
所以由根与系数的关系得,,
故,
当时,取得最小值4,所以最短弦长为4,故①正确,
②由①可知,则,
故以为直径的圆的圆心坐标为,半径,
抛物线的准线方程为,
故圆心到准线的距离,
所以以为直径的圆一定与抛物线的准线相切,故②正确,
③将代入,解得,所以当时,即在抛物线上,
当直线的斜率不存在时,方程为,此时只有一个交点,
当直线斜率存在且只与抛物线只有一个交点时,当且仅当该直线为切线时满足条件,
所以过点只与抛物线只有一个交点的直线有可能有2条,故③错误,
④因为抛物线的焦点为,又,,
所以三角形为直角三角形且过的切线斜率一定存在,
设的方程为,代入,可得,
由可得,即直线的倾斜角为,
因为直线过点且与垂直,所以一定平分,故④正确.
故答案为:①②④
三、解答题
17.已知某中学高三文科班学生共有800人参加了数学与地理的水平测试,现学校决定利用随机数表法从中抽取100人进行成绩统计,先将800人按001,002,003,…,800进行编号.
(1)如果从随机数表的第8行第7列的数开始向右读,请你依次写出最先抽取到的3个人的编号.
(2)所抽取的100人的数学与地理的水平测试成绩如下表:
人数 数学
优秀 良好 及格
地理 优秀 7 20 5
良好 9 18 6
及格 a 4 b
成绩分为优秀、良好、及格三个等级,横向、纵向分别表示地理成绩与数学成绩,例如表中数学成绩为良好的人数为20+18+4=42.若在该样本中,数学成绩优秀率为30%,求,的值.
(3)若,,求“在地理成绩为及格的学生中,数学成绩为优秀的人数比及格的人数少”的概率.
附:(下面摘取了随机数表的第7行至第9行)
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67
21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 55 67 19 98 10 50 71 75
12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38
15 51 00 13 42 99 66 02 79 54
(1)依题意知,最先抽取到的3个人的编号依次为785,567,199;
(2)由题意可得,解得.
因为,所以;
(3)由题意知,,,
则满足条件的有,,,,,,,,,,,,,,共组.
其中满足“在地理成绩为及格的学生中,数学成绩为优秀的人数比及格的人数少”的有,,,,,,共组.
故所求概率.
18.从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于和之间,将测量结果按如下方式分成八组:第一组,第二组,…,第八组,下图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人.
(1)求第七组的频率并估计该校800名男生中身高在以上(含)的人数;
(2)估计该校800名男生的身高中位数和平均数;
(3)从第六组和第八组的男生中随机抽取两名男生,记他们的身高分别为,,事件,求.
【答案】(1)0.06,144人;(2)中位数为,平均数为172.1;(3).
(1)第六组的频率为,
∴第七组的频率为,
由直方图得后三组频率为,
∴800名男生中身高在以上(含)的人数为人.
(2)由直方图得,身高在第一组的频率为,
身高在第二组的频率为,
身高在第三组的频率为,
身高在第四组的频率为,
由于,
,
设这所学校的800名男生的身高中位数为,
则,
由得,
所以这所学校的800名男生的身高的中位数为,
平均数为.
(3)第六组的人数为4人,设为,,,,
第八组的人数为人,设为,,
则从中随机抽取两名男生有,,,,,,,,,,,,,,共15种情况,
因事件发生当且仅当随机抽取的两名男生在同一组,所以事件包含的基本事件为,,,,,,共7种情况.
所以.
19.设命题实数满足;命题实数满足
(1)若,,都是真命题,求实数的取值范围;
(2)若是的充分不必要条件,求实数的取值范围.
【答案】(1);(2).
当时,由, 得命题,
由,所以命题,
若,都是真命题,则只需求解,即,
因此的取值范围是.
若是的充分不必要条件,则,
当时,则,所以不成立,
当时,解得:,,当时有:
,故的取值范围是.
20.如图,在四棱锥 P-ABCD中,△PAB为正三角形,四边形ABCD为矩形,且平面PAB⊥平面ABCD,AB=2,PC=4
(1)求证:平面PAB⊥平面PAD
(2)在线段PA上是否存在一点N,使得二面角A-BD-N的余弦值为若存在,求出点N的位置;若不存在,请说明理由
【答案】(1)证明见解析;(2)存在,点为的中点.
(1)证明:取的中点,连接,
∵为正三角形,∴,
又∵平面平面,且平面平面,
∴平面,
又平面,∴,
又∵,,且,
∴平面.
又∵平面,
∴平面平面.
(2)以O为原点建立如图所示的空间直角坐标系,
在直角中,,,∴
∴,
设,则,
则,,
设平面的一个法向量,
则,即,
令,可得得,
而平面的法向量,
由题意知:,解得(舍)或,
∴当点为的中点时,二面角的余弦值为.
21.(1)用分析法证明:当,时,;
(2)证明:对任意,,,这个值至少有一个不小于.
(1)要证不等式成立,只需证成立,
即证:成立,
即证:成立,
即证:成立,
因为所以,所以原不等式成立.
(2)假设这个值都小于,
即
则,(*)
而.
这与(*)矛盾,所以假设不成立,即原命题成立.
22.抛物线与直线有唯一公共点,且的焦点为.
(1)用含的式子表示.
(2)若点与关于直线对称,证明的纵坐标为定值.
解:(1)将代入,
,
∵与只有一个交点,故方程有两个相等的实数根,
.
(2)设,∵,
设为中点,∴,
在直线上,得①,
的斜率为,
则由与垂直可得,
故②
联立①②:,∵
∴点纵坐标为定值.
23.如图,在三棱柱中,已知是直角三角形,侧面是矩形,AB=BC=1,BB1=2,.
(1)证明:BC1⊥AC.
(2)E是棱CC1的中点,求直线B1C与平面ABE所成角的正弦值.
(1)证明:因为是直角三角形,所以AB⊥BC.
因为侧面是矩形,所以AB⊥BB1.
因为BC∩BB1=B,所以AB⊥平面BCC1B1,
又因为平面BCC1B1,所以AB⊥BC1.因为BC=1,BB1=CC1=2,,所以,所以BC⊥BC1.因为BC∩AB=B,所以BC1⊥平面ABC.因为平面ABC.所以BC1⊥AC.
(2)由(1)知,BC,BA,BC1两两垂直,故以B为坐标原点,分别以BC,BA,BC1为x,y,z轴正方向建立空间直角坐标系,如图所示:
则B(0,0,0),C(1,0,0),A(0,1,0),,.
,(2,0,),
设面ABE的法向量为,由,得,令z1=1,得.
设直线B1C与平面ABE所成角的大小为θ,则,
所以直线B1C与平面ABE所成角的正弦值为.
24.已知椭圆的中心在坐标原点,焦点在轴上,离心率为,右焦点到右顶点的距离为1.
(1)求椭圆的标准方程.
(2)是否存在与椭圆交于,两点的直线:,使得成立?若存在,求出实数的取值范围;若不存在,请说明理由.
(3)若动直线与椭圆有且仅有一个公共点,试问:在轴上是否存在两定点,使其到直线的距离之积为3?若存在,求出两定点坐标;若不存在,请说明理由.
(1)∵由题,,又∵,∴,,
∵,∴椭圆的方程为.
(2)设,,∵,∴,
∵,,∴
∵联立方程组,整理为 ,
其中,,,
∴,
∵,∴且,∴,
∴实数的取值范围是.
(3)设两定点为,,其中,①当直线不垂直于轴时,直线:,
∵联立方程组整理为,
其中 ,
∵两定点到直线的距离分别为,,
∴
或 ,
∴或对任意恒成立,
若对任意恒成立,则
∴,∴两定点为,.
又对任意不恒成立,
②当直线轴时,∵的方程为,或,
∴两定点为,到的距离之积为3,综上所述,存在两定点为,.
命题人: 审题人: 2021年1月9日
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.设P是双曲线=1(a>0,b>0)上的点,F1?F2是焦点,双曲线的离心率是,且∠F1PF2=90°,△F1PF2的面积是7,则a+b等于( )
A.3+ B.9+ C.10 D.16
2.为了保证抗击新型冠状肺炎期间的蔬菜供应,某大型超市统计了2月1号~10号连续天蔬菜进货量和出货量(单位:吨)如图所示,则下列说法错误的是( )
A.出货量的最高值与出货量的最低值的比是
B.天中剩余蔬菜最多的一天是2月4号
C.2月3号~4号的进货量的变化率比2月7号~8号进货量的变化率大
D.这10天每天平均剩余蔬菜为21吨
3.已知命题:且,都有;命题:,.则下列命题中为真命题的是( )
A. B. C. D.
4.如图,边长为的正方形中,点、分别是、的中点,将、、分别沿、、折起,使得、、三点重合于点,若四面体的四个顶点在同一个球面上,则该球的表面积为( ).
A.B.C.D.
5.新冠肺炎肆虐全,疫情波及多个国家和地区;一些国家宣布进入“紧急状态”,全球股市剧烈震荡……新冠肺炎疫情严重挑战公共卫生安全,全面冲击世界经济运行,深刻影响社会生活运转.这场全球公共卫生危机,需要国际社会的通力合作,在一次国际医学学术会议上,来自四个国家的五位代表被安排在一张圆桌就座,为了使他们能够自由交谈,事先了解到的情况如下:甲是中国人,还会说英语;乙是法国人,还会说日语;丙是英国人,还会说法语;丁是日本人,还会说汉语;戊是法国人,还会说德语;则这五位代表的座位顺序应为( )
A.甲丙丁戊乙 B.甲丁丙乙戊
C.甲乙丙丁戊 D.甲丙戊乙丁
6.设是正三棱锥,是的重心,是上的一点,且,若,则( ).
A. B. C. D.
7.设x1=17,x2=19,x3=20,x4=21,x5=23,将这五个数据依次输入如图程序框图进行计算,则输出的S值及其统计意义分别是( )
A.S=4,即5个数据的标准差为4 B.S=4,即5个数据的方差为4
C.S=20,即5个数据的方差为20 D.S=20,即5个数据的标准差为20
8.已知椭圆的左、右焦点分别为,为轴上一点,为正三角形,若,的中点恰好在椭圆上,则椭圆的离心率是( )
A. B. C.D.
9.如图,正方体的棱长为,、分别是棱、上的点,若平面,则与的长度之和为( ).
A.B.C.D.
10.已知,分别为椭圆()的左、右焦点,是椭圆上的一点,点在线段延长线上,且,过作直线于,则动点的轨迹为( ).
A.椭圆 B.抛物线 C.双曲线 D.圆
11.已知,是异面直线,,,,,,,,则异面直线,所成的角等于( )
A. B. C. D.
12.已知F1,F2为椭圆 (a>b>0)的两个焦点,B为椭圆短轴的一个端点,·≥2,则椭圆的离心率的取值范围为( )
A. B. C. D.
二、填空题
13.若“存在x∈[﹣1,1],成立”为真命题,则a的取值范围是___.
14.甲、乙两人下棋,两人下成和棋的概率是,甲获胜的概率是,则乙获胜的概率是_________.
15.长方体中,,设点关于直线对称点为,则点与点之间的距离是_________
16.对抛物线:,有下列命题:
①设直线:,则直线被抛物线所截得的最短弦长为4;
②已知直线:交抛物线于、两点,则以为直径的圆一定与抛物线的准线相切;
③过点与抛物线有且只有一个交点的直线有1条或3条;
④若抛物线的焦点为,抛物线上一点和抛物线内一点,过点作抛物线的切线,直线过点且与垂直,则平分;
其中你认为是正确命题的所有命题的序号是______.
三、解答题
17.已知某中学高三文科班学生共有800人参加了数学与地理的水平测试,现学校决定利用随机数表法从中抽取100人进行成绩统计,先将800人按001,002,003,…,800进行编号.
(1)如果从随机数表的第8行第7列的数开始向右读,请你依次写出最先抽取到的3个人的编号.
(2)所抽取的100人的数学与地理的水平测试成绩如下表:
人数 数学
优秀 良好 及格
地理 优秀 7 20 5
良好 9 18 6
及格 a 4 b
成绩分为优秀、良好、及格三个等级,横向、纵向分别表示地理成绩与数学成绩,例如表中数学成绩为良好的人数为20+18+4=42.若在该样本中,数学成绩优秀率为30%,求,的值.
(3)若,,求“在地理成绩为及格的学生中,数学成绩为优秀的人数比及格的人数少”的概率.
附:(下面摘取了随机数表的第7行至第9行)
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67
21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 55 67 19 98 10 50 71 75
12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38
15 51 00 13 42 99 66 02 79 54
18.从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于和之间,将测量结果按如下方式分成八组:第一组,第二组,…,第八组,下图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人.
(1)求第七组的频率并估计该校800名男生中身高在以上(含)的人数;
(2)估计该校800名男生的身高中位数和平均数;
(3)从第六组和第八组的男生中随机抽取两名男生,记他们的身高分别为,,事件,求.
19.设命题实数满足;命题实数满足
(1)若,,都是真命题,求实数的取值范围;
(2)若是的充分不必要条件,求实数的取值范围.
20.如图,在四棱锥 P-ABCD中,△PAB为正三角形,四边形ABCD为矩形,且平面PAB⊥平面ABCD,AB=2,PC=4
(1)求证:平面PAB⊥平面PAD
(2)在线段PA上是否存在一点N,使得二面角A-BD-N的余弦值为若存在,求出点N的位置;若不存在,请说明理由
21.(1)用分析法证明:当,时,;
(2)证明:对任意,,,这个值至少有一个不小于.
22.抛物线与直线有唯一公共点,且的焦点为.
(1)用含的式子表示.
(2)若点与关于直线对称,证明的纵坐标为定值.
23.如图,在三棱柱中,已知是直角三角形,侧面是矩形,AB=BC=1,BB1=2,.
(1)证明:BC1⊥AC.
(2)E是棱CC1的中点,求直线B1C与平面ABE所成角的正弦值.
24.已知椭圆的中心在坐标原点,焦点在轴上,离心率为,右焦点到右顶点的距离为1.
(1)求椭圆的标准方程.
(2)是否存在与椭圆交于,两点的直线:,使得成立?若存在,求出实数的取值范围;若不存在,请说明理由.
(3)若动直线与椭圆有且仅有一个公共点,试问:在轴上是否存在两定点,使其到直线的距离之积为3?若存在,求出两定点坐标;若不存在,请说明理由.
高二理复习卷数学
命题人: 审题人: 2021年1月9日
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.设P是双曲线=1(a>0,b>0)上的点,F1?F2是焦点,双曲线的离心率是,且∠F1PF2=90°,△F1PF2的面积是7,则a+b等于( )
A.3+ B.9+ C.10 D.16
由题意,不妨设点P是右支上的一点,|PF1|=m,|PF2|=n,则∴a=3,c=4.
∴b=.∴a+b=3+.故选:A
2.为了保证抗击新型冠状肺炎期间的蔬菜供应,某大型超市统计了2月1号~10号连续天蔬菜进货量和出货量(单位:吨)如图所示,则下列说法错误的是( )
A.出货量的最高值与出货量的最低值的比是
B.天中剩余蔬菜最多的一天是2月4号
C.2月3号~4号的进货量的变化率比2月7号~8号进货量的变化率大
D.这10天每天平均剩余蔬菜为21吨
【答案】A根据给定的2月1号~10号连续天蔬菜进货量和出货量(单位:吨)统计图表,
可得:出货量的最高值与出货量的最低值的比应是,所以A错误;
这天中,从每天的剩余吨数为:,其中2月4号剩余蔬菜量为吨,这是中,剩余蔬菜最多的一天,所以B正确;
2月3号~4号进货量的变化率为,2月7号~8号进货量变化率为,
所以2月3号~4号的进货量的变化率比2月7号~8号进货量的变化率大,所以C正确;
由,即这10天每天平均剩余蔬菜为21吨,所以D正确.
3.已知命题:且,都有;命题:,.则下列命题中为真命题的是( )
A. B. C. D.
当时,,所以命题是假命题,
因为恒成立,所以命题:,为假命题.
所以为真命题.故选:D
4.如图,边长为的正方形中,点、分别是、的中点,将、、分别沿、、折起,使得、、三点重合于点,若四面体的四个顶点在同一个球面上,则该球的表面积为( ).
A.B.C.D.
四面体为底面为等腰,顶点为的三棱锥,
则,,,,则,,
又,则为直角三角形,,
以为原点建立如图所示的空间直角坐标系,
则,,,,
设四面体的外接球的球心为,则,由空间两点间距离公式知:,,
,解得,,,
所以半径为,
所以该球的表面积为.
5.新冠肺炎肆虐全,疫情波及多个国家和地区;一些国家宣布进入“紧急状态”,全球股市剧烈震荡……新冠肺炎疫情严重挑战公共卫生安全,全面冲击世界经济运行,深刻影响社会生活运转.这场全球公共卫生危机,需要国际社会的通力合作,在一次国际医学学术会议上,来自四个国家的五位代表被安排在一张圆桌就座,为了使他们能够自由交谈,事先了解到的情况如下:甲是中国人,还会说英语;乙是法国人,还会说日语;丙是英国人,还会说法语;丁是日本人,还会说汉语;戊是法国人,还会说德语;则这五位代表的座位顺序应为( )
A.甲丙丁戊乙 B.甲丁丙乙戊
C.甲乙丙丁戊 D.甲丙戊乙丁
【答案】D
戊是法国人,还会说德语,只能用法语交流,则两侧只能是乙和丙,乙旁边是丁,丙旁边是甲,
6.设是正三棱锥,是的重心,是上的一点,且,若,则( ).
A. B. C. D.
如下图所示,连接并延长交于点,则点为的中点,
为的重心,可得,
而,
,
所以,,
所以,,因此,.
7.设x1=17,x2=19,x3=20,x4=21,x5=23,将这五个数据依次输入如图程序框图进行计算,则输出的S值及其统计意义分别是( )
A.S=4,即5个数据的标准差为4 B.S=4,即5个数据的方差为4
C.S=20,即5个数据的方差为20 D.S=20,即5个数据的标准差为20
数据,则,
根据程序框图进行计算,则输出
,它是计算这5个数据的方差.故选:B.
8.已知椭圆的左、右焦点分别为,为轴上一点,为正三角形,若,的中点恰好在椭圆上,则椭圆的离心率是( )
A. B. C.D.
因为为正三角形,所以,取线段的中点,连结,则,所以,得,所以椭圆的离心率.故选:A.
9.如图,正方体的棱长为,、分别是棱、上的点,若平面,则与的长度之和为( ).
A.B.C.D.
以为坐标原点,、、为、、轴建立空间直角坐标系,设,,
则,,,,
∴,,由于平面,
∴,即, 故与的长度之和为.故选:D.
10.已知,分别为椭圆()的左、右焦点,是椭圆上的一点,点在线段延长线上,且,过作直线于,则动点的轨迹为( ).
A.椭圆 B.抛物线 C.双曲线 D.圆
根据题意,即
故平分,又因为,设关于的对称点为,所以,
由椭圆定义可得,在中,为中位线,
故,所以(定值),故点的轨迹为圆.
11.已知,是异面直线,,,,,,,,则异面直线,所成的角等于( )
A. B. C. D.
【答案】C
,因为,故,所以,
而,故,所以,整理得到:,因为,故,故异面直线,所成的角为.
12.已知F1,F2为椭圆 (a>b>0)的两个焦点,B为椭圆短轴的一个端点,·≥2,则椭圆的离心率的取值范围为( )
A. B. C. D.
根据题意不妨设B(0,b),F1(-c,0),F2(c,0),
因为,所以,又因为b2=a2-c2,所以,即..故选:C.
二、填空题
13.若“存在x∈[﹣1,1],成立”为真命题,则a的取值范围是___.
【答案】
存在x∈[﹣1,1],成立,即在上有解,
设,,易得y=f(x)在[﹣1,1]为减函数,
所以,即,即,
即,所以,故答案为:.
14.甲、乙两人下棋,两人下成和棋的概率是,甲获胜的概率是,则乙获胜的概率是_________.
【答案】。因为事件“乙获胜”与事件“两人下和棋或甲获胜”互为对立事件,所以乙获胜的概率.故答案为:
15.长方体中,,设点关于直线对称点为,则点与点之间的距离是_________
【答案】
画出过点,线段的平面图如图所示:过点作于点,
因为点是点关于直线对称点,所以且平分,
所以,
因为长方体中,,
所以,,,
所以,,所以
,,在中由余弦定理得
,
16.对抛物线:,有下列命题:
①设直线:,则直线被抛物线所截得的最短弦长为4;
②已知直线:交抛物线于、两点,则以为直径的圆一定与抛物线的准线相切;
③过点与抛物线有且只有一个交点的直线有1条或3条;
④若抛物线的焦点为,抛物线上一点和抛物线内一点,过点作抛物线的切线,直线过点且与垂直,则平分;
其中你认为是正确命题的所有命题的序号是______.
【答案】①②④
①联立方程,消去可得,恒成立,
设两交点坐标分别为,,
所以由根与系数的关系得,,
故,
当时,取得最小值4,所以最短弦长为4,故①正确,
②由①可知,则,
故以为直径的圆的圆心坐标为,半径,
抛物线的准线方程为,
故圆心到准线的距离,
所以以为直径的圆一定与抛物线的准线相切,故②正确,
③将代入,解得,所以当时,即在抛物线上,
当直线的斜率不存在时,方程为,此时只有一个交点,
当直线斜率存在且只与抛物线只有一个交点时,当且仅当该直线为切线时满足条件,
所以过点只与抛物线只有一个交点的直线有可能有2条,故③错误,
④因为抛物线的焦点为,又,,
所以三角形为直角三角形且过的切线斜率一定存在,
设的方程为,代入,可得,
由可得,即直线的倾斜角为,
因为直线过点且与垂直,所以一定平分,故④正确.
故答案为:①②④
三、解答题
17.已知某中学高三文科班学生共有800人参加了数学与地理的水平测试,现学校决定利用随机数表法从中抽取100人进行成绩统计,先将800人按001,002,003,…,800进行编号.
(1)如果从随机数表的第8行第7列的数开始向右读,请你依次写出最先抽取到的3个人的编号.
(2)所抽取的100人的数学与地理的水平测试成绩如下表:
人数 数学
优秀 良好 及格
地理 优秀 7 20 5
良好 9 18 6
及格 a 4 b
成绩分为优秀、良好、及格三个等级,横向、纵向分别表示地理成绩与数学成绩,例如表中数学成绩为良好的人数为20+18+4=42.若在该样本中,数学成绩优秀率为30%,求,的值.
(3)若,,求“在地理成绩为及格的学生中,数学成绩为优秀的人数比及格的人数少”的概率.
附:(下面摘取了随机数表的第7行至第9行)
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67
21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 55 67 19 98 10 50 71 75
12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38
15 51 00 13 42 99 66 02 79 54
(1)依题意知,最先抽取到的3个人的编号依次为785,567,199;
(2)由题意可得,解得.
因为,所以;
(3)由题意知,,,
则满足条件的有,,,,,,,,,,,,,,共组.
其中满足“在地理成绩为及格的学生中,数学成绩为优秀的人数比及格的人数少”的有,,,,,,共组.
故所求概率.
18.从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于和之间,将测量结果按如下方式分成八组:第一组,第二组,…,第八组,下图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人.
(1)求第七组的频率并估计该校800名男生中身高在以上(含)的人数;
(2)估计该校800名男生的身高中位数和平均数;
(3)从第六组和第八组的男生中随机抽取两名男生,记他们的身高分别为,,事件,求.
【答案】(1)0.06,144人;(2)中位数为,平均数为172.1;(3).
(1)第六组的频率为,
∴第七组的频率为,
由直方图得后三组频率为,
∴800名男生中身高在以上(含)的人数为人.
(2)由直方图得,身高在第一组的频率为,
身高在第二组的频率为,
身高在第三组的频率为,
身高在第四组的频率为,
由于,
,
设这所学校的800名男生的身高中位数为,
则,
由得,
所以这所学校的800名男生的身高的中位数为,
平均数为.
(3)第六组的人数为4人,设为,,,,
第八组的人数为人,设为,,
则从中随机抽取两名男生有,,,,,,,,,,,,,,共15种情况,
因事件发生当且仅当随机抽取的两名男生在同一组,所以事件包含的基本事件为,,,,,,共7种情况.
所以.
19.设命题实数满足;命题实数满足
(1)若,,都是真命题,求实数的取值范围;
(2)若是的充分不必要条件,求实数的取值范围.
【答案】(1);(2).
当时,由, 得命题,
由,所以命题,
若,都是真命题,则只需求解,即,
因此的取值范围是.
若是的充分不必要条件,则,
当时,则,所以不成立,
当时,解得:,,当时有:
,故的取值范围是.
20.如图,在四棱锥 P-ABCD中,△PAB为正三角形,四边形ABCD为矩形,且平面PAB⊥平面ABCD,AB=2,PC=4
(1)求证:平面PAB⊥平面PAD
(2)在线段PA上是否存在一点N,使得二面角A-BD-N的余弦值为若存在,求出点N的位置;若不存在,请说明理由
【答案】(1)证明见解析;(2)存在,点为的中点.
(1)证明:取的中点,连接,
∵为正三角形,∴,
又∵平面平面,且平面平面,
∴平面,
又平面,∴,
又∵,,且,
∴平面.
又∵平面,
∴平面平面.
(2)以O为原点建立如图所示的空间直角坐标系,
在直角中,,,∴
∴,
设,则,
则,,
设平面的一个法向量,
则,即,
令,可得得,
而平面的法向量,
由题意知:,解得(舍)或,
∴当点为的中点时,二面角的余弦值为.
21.(1)用分析法证明:当,时,;
(2)证明:对任意,,,这个值至少有一个不小于.
(1)要证不等式成立,只需证成立,
即证:成立,
即证:成立,
即证:成立,
因为所以,所以原不等式成立.
(2)假设这个值都小于,
即
则,(*)
而.
这与(*)矛盾,所以假设不成立,即原命题成立.
22.抛物线与直线有唯一公共点,且的焦点为.
(1)用含的式子表示.
(2)若点与关于直线对称,证明的纵坐标为定值.
解:(1)将代入,
,
∵与只有一个交点,故方程有两个相等的实数根,
.
(2)设,∵,
设为中点,∴,
在直线上,得①,
的斜率为,
则由与垂直可得,
故②
联立①②:,∵
∴点纵坐标为定值.
23.如图,在三棱柱中,已知是直角三角形,侧面是矩形,AB=BC=1,BB1=2,.
(1)证明:BC1⊥AC.
(2)E是棱CC1的中点,求直线B1C与平面ABE所成角的正弦值.
(1)证明:因为是直角三角形,所以AB⊥BC.
因为侧面是矩形,所以AB⊥BB1.
因为BC∩BB1=B,所以AB⊥平面BCC1B1,
又因为平面BCC1B1,所以AB⊥BC1.因为BC=1,BB1=CC1=2,,所以,所以BC⊥BC1.因为BC∩AB=B,所以BC1⊥平面ABC.因为平面ABC.所以BC1⊥AC.
(2)由(1)知,BC,BA,BC1两两垂直,故以B为坐标原点,分别以BC,BA,BC1为x,y,z轴正方向建立空间直角坐标系,如图所示:
则B(0,0,0),C(1,0,0),A(0,1,0),,.
,(2,0,),
设面ABE的法向量为,由,得,令z1=1,得.
设直线B1C与平面ABE所成角的大小为θ,则,
所以直线B1C与平面ABE所成角的正弦值为.
24.已知椭圆的中心在坐标原点,焦点在轴上,离心率为,右焦点到右顶点的距离为1.
(1)求椭圆的标准方程.
(2)是否存在与椭圆交于,两点的直线:,使得成立?若存在,求出实数的取值范围;若不存在,请说明理由.
(3)若动直线与椭圆有且仅有一个公共点,试问:在轴上是否存在两定点,使其到直线的距离之积为3?若存在,求出两定点坐标;若不存在,请说明理由.
(1)∵由题,,又∵,∴,,
∵,∴椭圆的方程为.
(2)设,,∵,∴,
∵,,∴
∵联立方程组,整理为 ,
其中,,,
∴,
∵,∴且,∴,
∴实数的取值范围是.
(3)设两定点为,,其中,①当直线不垂直于轴时,直线:,
∵联立方程组整理为,
其中 ,
∵两定点到直线的距离分别为,,
∴
或 ,
∴或对任意恒成立,
若对任意恒成立,则
∴,∴两定点为,.
又对任意不恒成立,
②当直线轴时,∵的方程为,或,
∴两定点为,到的距离之积为3,综上所述,存在两定点为,.
同课章节目录
