五年级数学下册课件-8. 数学广角—找次品 -人教版(共24张PPT)
文档属性
| 名称 | 五年级数学下册课件-8. 数学广角—找次品 -人教版(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-16 00:00:00 | ||
图片预览






文档简介
(共24张PPT)
找次品
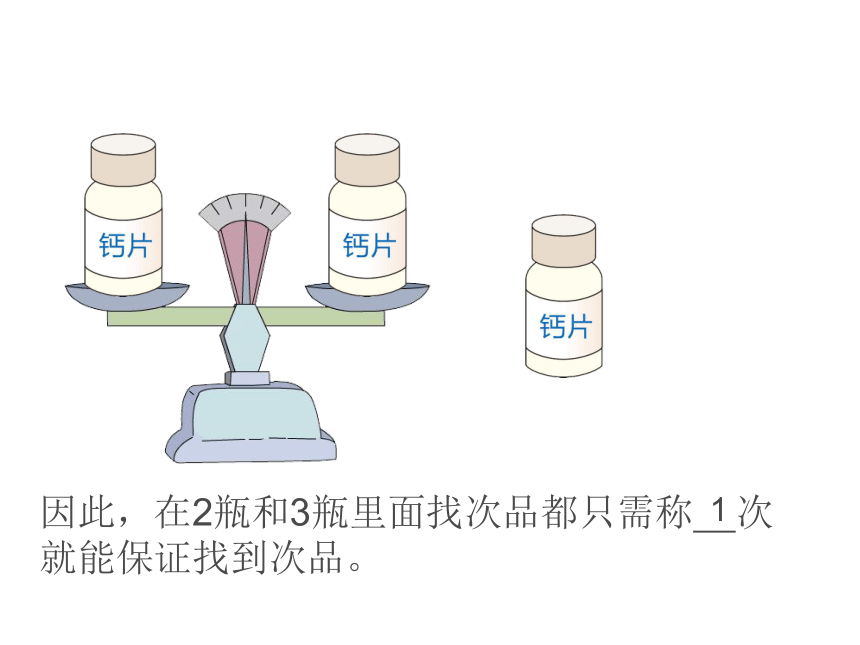
有3瓶钙片,其中1瓶是次品,少了3片。如果给你一架没有砝码的天平,你能设法把它找出来吗?
因此,在2瓶和3瓶里面找次品都只需称
次就能保证找到次品。
1
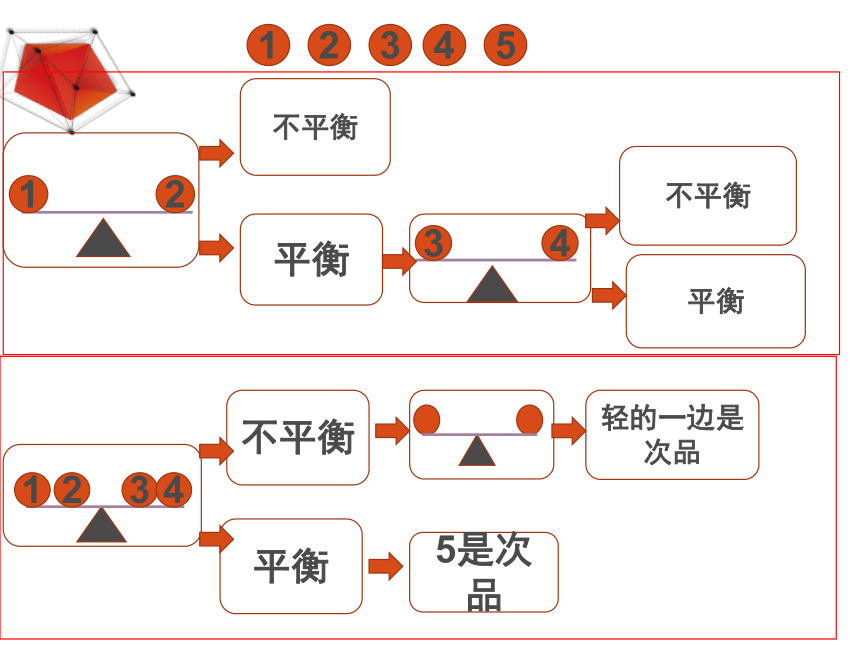
有5瓶钙片,其中1瓶是次品,少了3片。用天平称,至少几次能保证找出次品?
1
2
3
4
5
不平衡
平衡
不平衡
平衡
5是次品
不平衡
轻的一边是次品
1
2
1
2
3
4
3
4
平衡
思考:
在3个和5个里面找次品,哪种情况称的次数多?
当次品的范围缩小到3个或5个时,要保证找到次品,应该在哪里面找?
8个零件里有1个是次品(次品重一些),假如用天平称,至少称几次能保证一定找出次品?
小组讨论
1.总共有几种方法?
2.每次每边放几个?分成了几份?至少称几次找到次品?说一说称的过程。
要求:每人介绍一种分法。
3.哪种分法称的次数最少?
1
2
3
4
5
不平衡
平衡
不平衡
不平衡
6
1
2
3
4
5
6
7
8
平衡
7
8
8(3,3,2)
为什么把他们分成三份,称的次数最少呢?
称一次后,次品的范围缩小到2或3个。
2
3
4
5
6
7
1
8
1
2
3
4
5
6
7
8
称一次后,次品的范围缩小到4个.
称一次后,次品的范围缩小到几个?
9个零件里有1个是次品(次品重一些),假如用天平称,至少称几次能保证一定找出次品?
1
2
3
4
5
6
(3,3,3)
7
8
9
1
2
3
4
5
6
(3,3,2)
7
8
对比,发现它们有什么共同之处?试着总结找次品的方法。
方法:1.把待测物分成三份;
2.尽量平均分(不能平均分的,也应使
多的一份和少一份的只相差1)。
练习
10个零件里有1个是次品(次品重一些),假如用天平称,至少称几次能保证一定找出次品?
10(3,3,4)——4(1,1,2)——2(1,1)
答:至少称3次找到次品。
当堂检测
有15盒饼干,其中14盒质量相同,另有1盒少了几块,如果能用天平称,至少几次可以保证找出这盒饼干?
分析:15(5,5,5)——5(2,2,1)——2(1,1)
答:至少3次找到这盒饼干。
1次最多能在多少瓶中找出次品?2次呢?
1次最多能在3瓶中找出次品,
2次最多能在9个物品中找出次品。
练习
有28瓶水,其中27瓶质量相同,另有1瓶是盐水,比其他的水略重一些。至少称几次能保证找出这瓶盐水?
28(9,9,10)——10(3,3,4)——4(1,1,2)——2(1,1);
答:至少称4次能保证找出这瓶盐水。
1
2
3
4
5
不平衡,则
(
)(填轻或重)的一边是次品
平衡1、2(
)(是或不是)次品
不平衡则(
)(填轻或重)的一边有次品
平衡则1、2、3、4(
)(是或不是)次品。
(
)是次品
不平衡则(
)的一边是次品
不平衡则(
)(填轻或重)的一边是次品
1
2
1
2
3
4
3
4
平衡则(
)是次品
1
2
3
4
5
1
不平衡
平衡,次品在7、8、9中
不平衡则找到次品
不平衡则找到次品
6
7
8
2
3
4
5
6
7
8
平衡则未称的是次品
(3,3,3)
9
平衡则未称的是次品
小组合作
1.把零件分成几份?每份是多少?
2.假如天平平衡,次品在哪里?
3.假如天平不平衡,次品又在哪里?
4.至少称几次能保证找出次品?
分组探究拿出棋子代替零件,模拟天平称的过程,并在学习单上记录每次称的过程。
(1)1
箱糖果有
12
袋,其中有
11
袋质量相同,另有
1
袋质量不足,轻一些。至少称几次能保证找出这袋糖果来?
把
12
袋糖分成
3
份,每份
4
袋。
天平两边各放
4
袋。
平衡
不平衡
则次品
在轻的
一边,
天平两
边各放
1袋,
再称,
平衡
不平衡
则天平两端不
是次品,剩下
两袋,再称。
则找到次品。
则天平两端不
是次品,剩下
的两袋再称。
则找到次品。
平衡
不平衡
当堂检测
则天平两端不是次品,次品在剩下的4袋中,天平两端各放一袋再称。
找次品
有3瓶钙片,其中1瓶是次品,少了3片。如果给你一架没有砝码的天平,你能设法把它找出来吗?
因此,在2瓶和3瓶里面找次品都只需称
次就能保证找到次品。
1
有5瓶钙片,其中1瓶是次品,少了3片。用天平称,至少几次能保证找出次品?
1
2
3
4
5
不平衡
平衡
不平衡
平衡
5是次品
不平衡
轻的一边是次品
1
2
1
2
3
4
3
4
平衡
思考:
在3个和5个里面找次品,哪种情况称的次数多?
当次品的范围缩小到3个或5个时,要保证找到次品,应该在哪里面找?
8个零件里有1个是次品(次品重一些),假如用天平称,至少称几次能保证一定找出次品?
小组讨论
1.总共有几种方法?
2.每次每边放几个?分成了几份?至少称几次找到次品?说一说称的过程。
要求:每人介绍一种分法。
3.哪种分法称的次数最少?
1
2
3
4
5
不平衡
平衡
不平衡
不平衡
6
1
2
3
4
5
6
7
8
平衡
7
8
8(3,3,2)
为什么把他们分成三份,称的次数最少呢?
称一次后,次品的范围缩小到2或3个。
2
3
4
5
6
7
1
8
1
2
3
4
5
6
7
8
称一次后,次品的范围缩小到4个.
称一次后,次品的范围缩小到几个?
9个零件里有1个是次品(次品重一些),假如用天平称,至少称几次能保证一定找出次品?
1
2
3
4
5
6
(3,3,3)
7
8
9
1
2
3
4
5
6
(3,3,2)
7
8
对比,发现它们有什么共同之处?试着总结找次品的方法。
方法:1.把待测物分成三份;
2.尽量平均分(不能平均分的,也应使
多的一份和少一份的只相差1)。
练习
10个零件里有1个是次品(次品重一些),假如用天平称,至少称几次能保证一定找出次品?
10(3,3,4)——4(1,1,2)——2(1,1)
答:至少称3次找到次品。
当堂检测
有15盒饼干,其中14盒质量相同,另有1盒少了几块,如果能用天平称,至少几次可以保证找出这盒饼干?
分析:15(5,5,5)——5(2,2,1)——2(1,1)
答:至少3次找到这盒饼干。
1次最多能在多少瓶中找出次品?2次呢?
1次最多能在3瓶中找出次品,
2次最多能在9个物品中找出次品。
练习
有28瓶水,其中27瓶质量相同,另有1瓶是盐水,比其他的水略重一些。至少称几次能保证找出这瓶盐水?
28(9,9,10)——10(3,3,4)——4(1,1,2)——2(1,1);
答:至少称4次能保证找出这瓶盐水。
1
2
3
4
5
不平衡,则
(
)(填轻或重)的一边是次品
平衡1、2(
)(是或不是)次品
不平衡则(
)(填轻或重)的一边有次品
平衡则1、2、3、4(
)(是或不是)次品。
(
)是次品
不平衡则(
)的一边是次品
不平衡则(
)(填轻或重)的一边是次品
1
2
1
2
3
4
3
4
平衡则(
)是次品
1
2
3
4
5
1
不平衡
平衡,次品在7、8、9中
不平衡则找到次品
不平衡则找到次品
6
7
8
2
3
4
5
6
7
8
平衡则未称的是次品
(3,3,3)
9
平衡则未称的是次品
小组合作
1.把零件分成几份?每份是多少?
2.假如天平平衡,次品在哪里?
3.假如天平不平衡,次品又在哪里?
4.至少称几次能保证找出次品?
分组探究拿出棋子代替零件,模拟天平称的过程,并在学习单上记录每次称的过程。
(1)1
箱糖果有
12
袋,其中有
11
袋质量相同,另有
1
袋质量不足,轻一些。至少称几次能保证找出这袋糖果来?
把
12
袋糖分成
3
份,每份
4
袋。
天平两边各放
4
袋。
平衡
不平衡
则次品
在轻的
一边,
天平两
边各放
1袋,
再称,
平衡
不平衡
则天平两端不
是次品,剩下
两袋,再称。
则找到次品。
则天平两端不
是次品,剩下
的两袋再称。
则找到次品。
平衡
不平衡
当堂检测
则天平两端不是次品,次品在剩下的4袋中,天平两端各放一袋再称。
