冀 教版 九年级 上册 26.4 解直角三角形的应用 同步练习(Word版 含解析)
文档属性
| 名称 | 冀 教版 九年级 上册 26.4 解直角三角形的应用 同步练习(Word版 含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 340.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-16 17:21:42 | ||
图片预览

文档简介
解直角三角形的应用同步练习
一、选择题
如图所示的木制活动衣帽架是由三个全等的菱形构成,根据实际需要可以调节AE间的距离.若AE间的距离调节到60cm,菱形的边长,则的度数是
A.
B.
C.
D.
如图,有一斜坡AB的长米,坡角,则斜坡AB的铅垂高度AC为
A.
B.
C.
D.
如图,两根竹竿AB和AD斜靠在墙CE上,量得,,则竹竿AB与AD的长度之比为
A.
B.
C.
D.
如图,在离铁塔150米的A处,用测倾仪测得塔顶的仰角为,测倾仪高AD为米,则铁塔的高BC为
A.
米
B.
米
C.
米
D.
米
如图,在A处测得点P在北偏东方向上,在B处测得点P在北偏东方向上,若米,则点P到直线AB距离PC为
A.
3米
B.
米
C.
2米
D.
1米
如图是墙壁上在,两条平行线间边长为a的正方形瓷砖,该瓷砖与平行线的较大夹角为a,则两条平行线间的距离为
A.
B.
C.
D.
下列说法正确的是
A.
对角线相等且互相垂直的四边形是正方形
B.
坡面的水平宽度与铅直高度的比称为坡度
C.
两个相似图形也是位似图形
D.
平分弦不是直径的直径垂直于弦,并且平分弦所对的弧
如图,为了测量河岸A,B两点的距离,在与AB垂直的方向上取点C,测得,,那么AB等于
A.
B.
C.
D.
图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘,且与闸机侧立面夹角当双翼收起时,可以通过闸机的物体的最大宽度为
A.
B.
C.
64?cm
D.
54
cm
如图,社会实践活动小组实地测量两岸互相平行的一段河的宽度,河的南岸点A处,测得河的北岸边点B在其北偏东方向,然后向西走60米到达C点,测得点B在点C的北偏东方向,则这段河的宽度为.
A.
米
B.
米
C.
米
D.
米
如图是拦水坝的横断面,斜坡AB的水平宽度为12米,斜面坡度为,则斜坡AB的长为
A.
米
B.
米
C.
米
D.
24米
如图,港口A在观测站O的正东方向,,某船从港口A出发,沿北偏东方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东的方向,则该船航行的距离即AB的长为????
A.
km
B.
C.
D.
二、填空题
如图,某河堤迎水坡AB的坡比,堤高,则坡面AB的长是________m.
活动楼梯如图所示,,斜坡AC的坡度为1:1,斜坡AC的坡面长度为8m,则走这个活动楼梯从A点到C点上升的高度BC为______.
为做好疫情宣传巡查工作,各地积极借助科技手段加大防控力度.如图,亮亮在外出期间被无人机隔空喊话“戴上口罩,赶紧回家”据测量,无人机与亮亮的水平距离是15米,当他抬头仰视无人机时,仰角恰好为,若亮亮身高米,则无人机距离地面的高度约为______米.结果精确到米,参考数据:,
一斜面的坡度:,一物体由斜面底部沿斜面向前推了15米,那么这个物体升高了______米.
某厂家新开发的一种电动车如图,它的大灯A射出的光线AB、AC与地面MN所夹的锐角分别是和大灯A离地面的距离为1m,则该车大灯照亮地面的宽度BC是________不考虑其他因素,保留一位整数参考数据:,,,
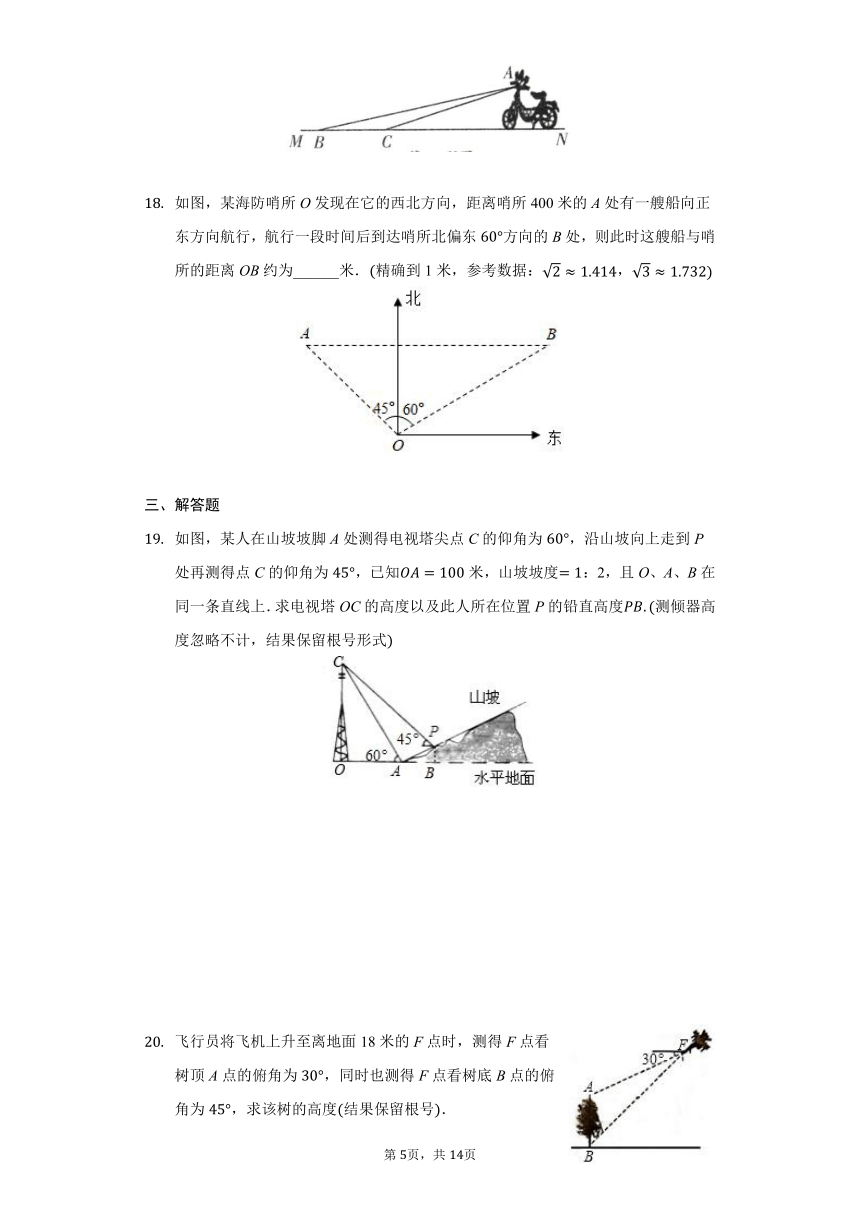
如图,某海防哨所O发现在它的西北方向,距离哨所400米的A处有一艘船向正东方向航行,航行一段时间后到达哨所北偏东方向的B处,则此时这艘船与哨所的距离OB约为______米.精确到1米,参考数据:,
三、解答题
如图,某人在山坡坡脚A处测得电视塔尖点C的仰角为,沿山坡向上走到P处再测得点C的仰角为,已知米,山坡坡度:2,且O、A、B在同一条直线上.求电视塔OC的高度以及此人所在位置P的铅直高度测倾器高度忽略不计,结果保留根号形式
飞行员将飞机上升至离地面18米的F点时,测得F点看树顶A点的俯角为,同时也测得F点看树底B点的俯角为,求该树的高度结果保留根号.
某高速公路建设中,需要确定隧道AB的长度.已知在离地面1800m高度C处的飞机上,测量人员测得正前方A,B两点处的俯角分别为和即,求隧道AB的长.结果保留根号
如图,A,B两点被池塘隔开,在AB外选一点C,连接AC,测得,,根据测得的数据,求AB的长结果取整数.
参考数据:,,.
答案和解析
1.【答案】C
【解析】解:连结AE,
间的距离调节到60cm,木制活动衣帽架是由三个全等的菱形构成,
,
菱形的边长,
,
,
是等边三角形,
,
.
2.【答案】A
【解析】解:由题意可得:,
即,
故AC.
3.【答案】B
【解答】
解:在中,,
在中,,
::,
故选:B.
4.【答案】A
【解析】解:过点A作,E为垂足,如图所示:
则四边形ADCE为矩形,,
,
在中,,
,
,
5.【答案】B
【解析】解:设点P到直线AB距离PC为x米,
在中,,
在中,,
由题意得,,
解得,米,
6.【答案】B
【解析】解:如图,过B作于点E,EF与交于点F,则,
四边形ABCD是正方形,
,,
,
,
,
≌,
,
在中,,,
,
,
即两条平行线间的距离为,
7.【答案】D
【解析】解:A、对角线相等且互相垂直的平行四边形是正方形,故此选项错误;
B、坡面的铅直高度与水平宽度的比称为坡度,故此选项错误;
C、两个相似图形不一定位似图形,故此选项错误;
D、平分弦不是直径的直径垂直于弦,并且平分弦所对的弧,正确.
8.【答案】C
【解答】
解:,,
在直角中,,
.
故选C.
9.【答案】C
【解答】
解:过A作于E,过B作于F,
在中,,
同理可得,,又与B之间的距离为10cm,
通过闸机的物体的最大宽度为.
故选C.
10.【答案】B
【解析】
【分析】.
作交CA的延长线于D,设,根据正切的定义用x表示出CD、AD,根据题意列出方程,解方程即可.
【解答】
解:作交CA的延长线于D,
设,
,
,
,
,
则,
解得,
答:这段河的宽约为米.
故选:B.
11.【答案】B
【解答】
解:过点B作BE垂直于AD,
斜面坡度为,,
,
则.
故选B.
12.【答案】C
【解答】
解:如图,过点A作于D.
在中,,,,
.
在中,,,
,
.
即该船航行的距离即AB的长为.
故选C.
13.【答案】10
【解答】
解:坡比,,
,
,
又,
,
故答案为:10.
?
14.【答案】
【解析】解:如图.米,BC::1.
设米,则米.
在中,,
即,
解得,
即米.
故上升高度是米.
15.【答案】
【解析】解:如图,
根据题意可知:
,,
过点D作于点C,
所以四边形DEBC是矩形,
,
,
在中,,
,
即,
解得,
米.
16.【答案】12
【解析】解:如图所示:
坡度:,
:::3,
设,则,
,
,
,
解得:,
,
即这个物体升高了12米;
17.【答案】
【解析】解:作,垂足为D.
由题意得:,,
在中,,
即,
,
中,,
即,
,
解得.
18.【答案】566
【解答】
解:如图,设线段AB交y轴于C,
在直角中,,则.
米,
米.
在直角中,,米,
米.
故答案是:566.
19.【答案】解:作于点E,过点P作,垂足为F.
在中,由,,得米,
过点P作,垂足为B.
由:2,设,则.
,.
在中,由,
,即,
,即米.
20.【答案】解:过F作交BA的延长线于C,
则,,,
,
,
,
答:该树的高度为米.
21.【答案】解:由题意得,,
,,
.
答:隧道AB的长为.
22.【答案】解:如图,过点A作,垂足为D,
,
,
设,
在中,,,
又,即,
,
解得,,
第2页,共2页
第1页,共1页
一、选择题
如图所示的木制活动衣帽架是由三个全等的菱形构成,根据实际需要可以调节AE间的距离.若AE间的距离调节到60cm,菱形的边长,则的度数是
A.
B.
C.
D.
如图,有一斜坡AB的长米,坡角,则斜坡AB的铅垂高度AC为
A.
B.
C.
D.
如图,两根竹竿AB和AD斜靠在墙CE上,量得,,则竹竿AB与AD的长度之比为
A.
B.
C.
D.
如图,在离铁塔150米的A处,用测倾仪测得塔顶的仰角为,测倾仪高AD为米,则铁塔的高BC为
A.
米
B.
米
C.
米
D.
米
如图,在A处测得点P在北偏东方向上,在B处测得点P在北偏东方向上,若米,则点P到直线AB距离PC为
A.
3米
B.
米
C.
2米
D.
1米
如图是墙壁上在,两条平行线间边长为a的正方形瓷砖,该瓷砖与平行线的较大夹角为a,则两条平行线间的距离为
A.
B.
C.
D.
下列说法正确的是
A.
对角线相等且互相垂直的四边形是正方形
B.
坡面的水平宽度与铅直高度的比称为坡度
C.
两个相似图形也是位似图形
D.
平分弦不是直径的直径垂直于弦,并且平分弦所对的弧
如图,为了测量河岸A,B两点的距离,在与AB垂直的方向上取点C,测得,,那么AB等于
A.
B.
C.
D.
图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘,且与闸机侧立面夹角当双翼收起时,可以通过闸机的物体的最大宽度为
A.
B.
C.
64?cm
D.
54
cm
如图,社会实践活动小组实地测量两岸互相平行的一段河的宽度,河的南岸点A处,测得河的北岸边点B在其北偏东方向,然后向西走60米到达C点,测得点B在点C的北偏东方向,则这段河的宽度为.
A.
米
B.
米
C.
米
D.
米
如图是拦水坝的横断面,斜坡AB的水平宽度为12米,斜面坡度为,则斜坡AB的长为
A.
米
B.
米
C.
米
D.
24米
如图,港口A在观测站O的正东方向,,某船从港口A出发,沿北偏东方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东的方向,则该船航行的距离即AB的长为????
A.
km
B.
C.
D.
二、填空题
如图,某河堤迎水坡AB的坡比,堤高,则坡面AB的长是________m.
活动楼梯如图所示,,斜坡AC的坡度为1:1,斜坡AC的坡面长度为8m,则走这个活动楼梯从A点到C点上升的高度BC为______.
为做好疫情宣传巡查工作,各地积极借助科技手段加大防控力度.如图,亮亮在外出期间被无人机隔空喊话“戴上口罩,赶紧回家”据测量,无人机与亮亮的水平距离是15米,当他抬头仰视无人机时,仰角恰好为,若亮亮身高米,则无人机距离地面的高度约为______米.结果精确到米,参考数据:,
一斜面的坡度:,一物体由斜面底部沿斜面向前推了15米,那么这个物体升高了______米.
某厂家新开发的一种电动车如图,它的大灯A射出的光线AB、AC与地面MN所夹的锐角分别是和大灯A离地面的距离为1m,则该车大灯照亮地面的宽度BC是________不考虑其他因素,保留一位整数参考数据:,,,
如图,某海防哨所O发现在它的西北方向,距离哨所400米的A处有一艘船向正东方向航行,航行一段时间后到达哨所北偏东方向的B处,则此时这艘船与哨所的距离OB约为______米.精确到1米,参考数据:,
三、解答题
如图,某人在山坡坡脚A处测得电视塔尖点C的仰角为,沿山坡向上走到P处再测得点C的仰角为,已知米,山坡坡度:2,且O、A、B在同一条直线上.求电视塔OC的高度以及此人所在位置P的铅直高度测倾器高度忽略不计,结果保留根号形式
飞行员将飞机上升至离地面18米的F点时,测得F点看树顶A点的俯角为,同时也测得F点看树底B点的俯角为,求该树的高度结果保留根号.
某高速公路建设中,需要确定隧道AB的长度.已知在离地面1800m高度C处的飞机上,测量人员测得正前方A,B两点处的俯角分别为和即,求隧道AB的长.结果保留根号
如图,A,B两点被池塘隔开,在AB外选一点C,连接AC,测得,,根据测得的数据,求AB的长结果取整数.
参考数据:,,.
答案和解析
1.【答案】C
【解析】解:连结AE,
间的距离调节到60cm,木制活动衣帽架是由三个全等的菱形构成,
,
菱形的边长,
,
,
是等边三角形,
,
.
2.【答案】A
【解析】解:由题意可得:,
即,
故AC.
3.【答案】B
【解答】
解:在中,,
在中,,
::,
故选:B.
4.【答案】A
【解析】解:过点A作,E为垂足,如图所示:
则四边形ADCE为矩形,,
,
在中,,
,
,
5.【答案】B
【解析】解:设点P到直线AB距离PC为x米,
在中,,
在中,,
由题意得,,
解得,米,
6.【答案】B
【解析】解:如图,过B作于点E,EF与交于点F,则,
四边形ABCD是正方形,
,,
,
,
,
≌,
,
在中,,,
,
,
即两条平行线间的距离为,
7.【答案】D
【解析】解:A、对角线相等且互相垂直的平行四边形是正方形,故此选项错误;
B、坡面的铅直高度与水平宽度的比称为坡度,故此选项错误;
C、两个相似图形不一定位似图形,故此选项错误;
D、平分弦不是直径的直径垂直于弦,并且平分弦所对的弧,正确.
8.【答案】C
【解答】
解:,,
在直角中,,
.
故选C.
9.【答案】C
【解答】
解:过A作于E,过B作于F,
在中,,
同理可得,,又与B之间的距离为10cm,
通过闸机的物体的最大宽度为.
故选C.
10.【答案】B
【解析】
【分析】.
作交CA的延长线于D,设,根据正切的定义用x表示出CD、AD,根据题意列出方程,解方程即可.
【解答】
解:作交CA的延长线于D,
设,
,
,
,
,
则,
解得,
答:这段河的宽约为米.
故选:B.
11.【答案】B
【解答】
解:过点B作BE垂直于AD,
斜面坡度为,,
,
则.
故选B.
12.【答案】C
【解答】
解:如图,过点A作于D.
在中,,,,
.
在中,,,
,
.
即该船航行的距离即AB的长为.
故选C.
13.【答案】10
【解答】
解:坡比,,
,
,
又,
,
故答案为:10.
?
14.【答案】
【解析】解:如图.米,BC::1.
设米,则米.
在中,,
即,
解得,
即米.
故上升高度是米.
15.【答案】
【解析】解:如图,
根据题意可知:
,,
过点D作于点C,
所以四边形DEBC是矩形,
,
,
在中,,
,
即,
解得,
米.
16.【答案】12
【解析】解:如图所示:
坡度:,
:::3,
设,则,
,
,
,
解得:,
,
即这个物体升高了12米;
17.【答案】
【解析】解:作,垂足为D.
由题意得:,,
在中,,
即,
,
中,,
即,
,
解得.
18.【答案】566
【解答】
解:如图,设线段AB交y轴于C,
在直角中,,则.
米,
米.
在直角中,,米,
米.
故答案是:566.
19.【答案】解:作于点E,过点P作,垂足为F.
在中,由,,得米,
过点P作,垂足为B.
由:2,设,则.
,.
在中,由,
,即,
,即米.
20.【答案】解:过F作交BA的延长线于C,
则,,,
,
,
,
答:该树的高度为米.
21.【答案】解:由题意得,,
,,
.
答:隧道AB的长为.
22.【答案】解:如图,过点A作,垂足为D,
,
,
设,
在中,,,
又,即,
,
解得,,
第2页,共2页
第1页,共1页
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
