5.1 相交线 课时训练(含解析)
图片预览



文档简介
中小学教育资源及组卷应用平台
2021年七年级数学下册课时训练:5.1《相交线》
班级__________姓名__________学号__________
一.选择题(共7小题)
1.如图图形中,∠1与∠2是对顶角的有( )
A.B.C.D.
2.如图,∠B的内错角是( )
A.∠1 B.∠2 C.∠3 D.∠4
3.平面内三条两两相交的直线( )
A.有一个交点 B.有一个或三个交点
C.有三个交点 D.上述都不对
4.如图,点O在直线AB上,CO⊥AB,若∠COD=52°,则∠AOD的度数是( )
A.38° B.128° C.142° D.150°
5.如图,把河AB中的水引到C,拟修水渠中最短的是( )
A.CM B.CN C.CP D.CQ
6.下列所示的四个图形中,∠1和∠2是同位角的是( )
A.②③ B.①②③ C.③④ D.①②④
7.∠1的对顶角是∠2,∠2的邻补角是∠3,若∠3=50°,则∠1的度数是( )
A.40° B.50° C.130° D.50°或130°
二.填空题(共7小题)
8.从直线外一点到这条直线的 ,叫做该点到直线的距离.
9.如图,与∠1是同旁内角的是 ,与∠2是内错角的是 .
10.如图,AH⊥BC,垂足为H,若AB=1.7cm,AC=2cm,AH=1.2cm,则点A到直线BC的距离是 ________cm.
11.如图,两直线交于点O,若∠1+∠2=76°,则∠1= 度.
12.若∠1=64°,则∠1的邻补角度数为 .
13.如图所示的图形中,同位角有 对.
14.如图,直线a、b相交,∠1=36°,则∠2﹣∠3= .
三.解答题(共6小题)
15.如图,有两堵围墙,有人想测量地面上两堵围墙内所形成的∠AOB的度数,但人又不能进入围墙,只能站在墙外,请问该如何测量?
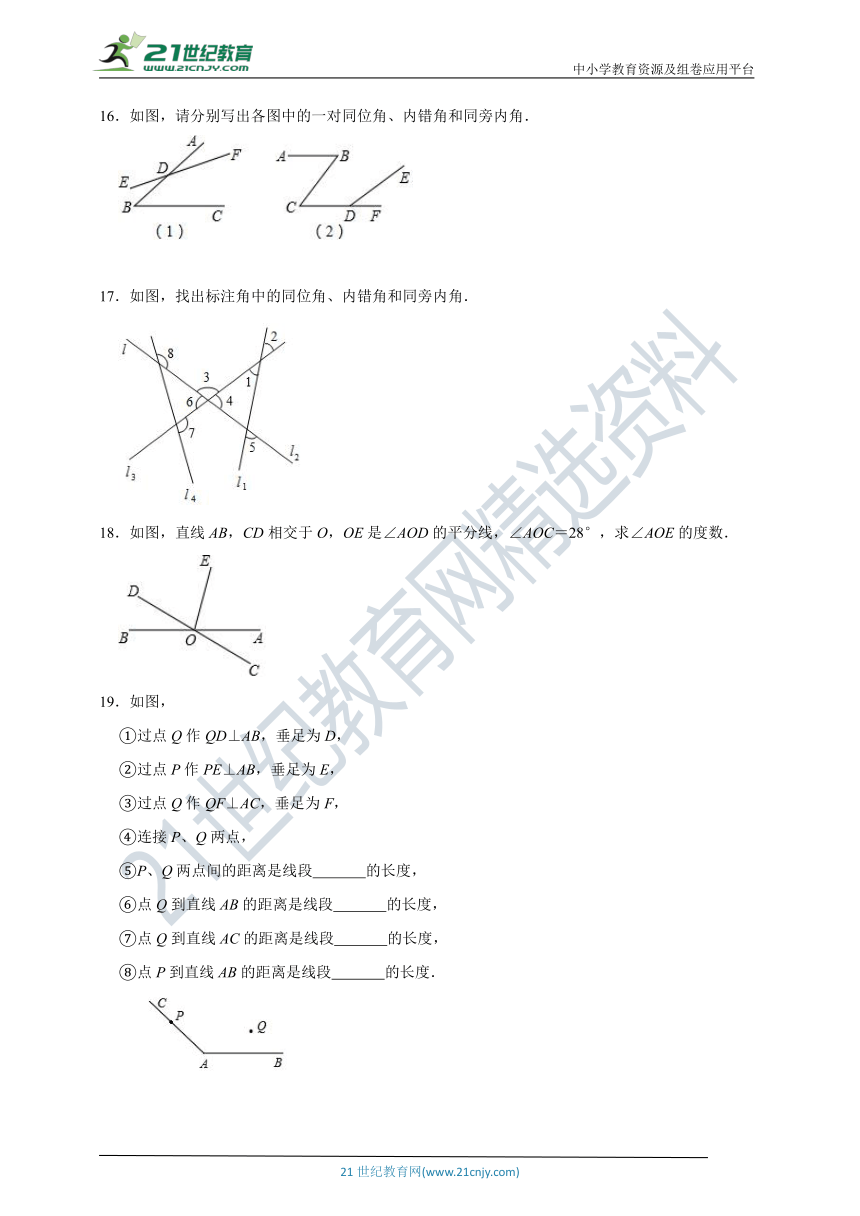
16.如图,请分别写出各图中的一对同位角、内错角和同旁内角.
17.如图,找出标注角中的同位角、内错角和同旁内角.
18.如图,直线AB,CD相交于O,OE是∠AOD的平分线,∠AOC=28°,求∠AOE的度数.
19.如图,
①过点Q作QD⊥AB,垂足为D,
②过点P作PE⊥AB,垂足为E,
③过点Q作QF⊥AC,垂足为F,
④连接P、Q两点,
⑤P、Q两点间的距离是线段 的长度,
⑥点Q到直线AB的距离是线段 的长度,
⑦点Q到直线AC的距离是线段 的长度,
⑧点P到直线AB的距离是线段 的长度.
20.如图所示,码头、火车站分别位于A,B两点,直线a和b分别表示铁路与河流.
(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
参考答案
一.选择题(共7小题)
1.【解答】解:B、C、D选项中的∠1与∠2都不是对顶角,
A选项中的∠1与∠2都是对顶角,
故选:A.
2.【解答】解:A、∠B的内错角是∠1,故此选项符合题意;
B、∠B与∠2是同旁内角,故此选项不合题意;
C、∠B与∠3是同位角,故此选项不合题意;
D、∠B与∠4是不是内错角,故此选项不合题意;
故选:A.
3.【解答】解:如图,
三条直线两两相交时,共有3个交点;三条直线相交于一点时,有一个交点.
故选:B.
4.【解答】解:如图所示:∵CO⊥AB,
∴∠AOC=90°,
∵∠COD=52°,
∴∠AOD=∠AOC+∠COD=90°+52°=142°.
故选:C.
5.【解答】解:如图,CP⊥AB,垂足为P,
在P处开水渠,则水渠最短.
因为直线外一点与直线上各点连线的所有线段中,垂线段最短.
故选:C.
6.【解答】解:图①②④中,∠1和∠2是同位角,
故选:D.
7.【解答】解:∵∠2的邻补角是∠3,∠3=50°,
∴∠2=130°,
∵∠1的对顶角是∠2,
∴∠1=130°,
故选:C.
二.填空题(共7小题)
8.【解答】解:从直线外一点到这条直线的垂线段的长度,叫做该点到直线的距离.
故答案为:垂线段的长度.
9.【解答】解:如图,与∠1是同旁内角的是∠5,与∠2是内错角的是∠3.
故答案为:∠5;∠3.
10.【解答】解:∵AH⊥BC,AH=1.2cm,
∴点A到直线BC的距离是1.2cm,
故答案为:1.2.
11.【解答】解:∵两直线交于点O,
∴∠1=∠2,
∵∠1+∠2=76°,
∴∠1=38°.
故答案为:38.
12.【解答】解:∵∠1=64°,
∴∠1的邻补角度数为:180°﹣64°=116°.
故答案为:116°.
13.【解答】解:如图:
∠CAG的同位角是∠DBG,∠EAG的同位角是∠FBG,
∴图中同位角有2对.
故答案为:2.
14.【解答】解:∵直线a、b相交,∠1=36°,
∴∠3=∠1=36°,∠2=180°﹣∠1=144°,
∴∠2﹣∠3=144°﹣36°=108°.
故答案为:108°.
三.解答题(共6小题)
15.【解答】解:如图,延长AO,先测量出∠BOC的度数,然后根据∠AOB与∠BOC是邻补角即可求解,
∠AOB=180°﹣∠BOC.
16.【解答】解:同位角是∠ADF与∠ABC,∠EDF与∠BCD,
内错角是∠EDB与∠DBC,∠ABC与∠BCD,
同旁内角是∠FDB与∠DBC,∠BCD与∠CDE.
17.【解答】解:同位角有∠4与∠8、∠4与∠7、∠2与∠3;
内错角有∠1与∠3、∠7与∠6、∠6与∠8;
同旁内角有∠1与∠4、∠3与∠8,∠1与∠7.
18.【解答】解:∵∠AOC+∠AOD=180°,∠AOC=28°,
∴∠AOD=152°.
∵OE平分∠AOD,
∴∠AOE=∠AOD=76°.
19.【解答】解:①②③④作图如图所示:
⑤根据两点之间距离即可得出P、Q两点间的距离是线段PQ的长度,
⑥根据点到直线的距离可得出点Q到直线AB的距离是线段QD的长度,
⑦根据点到直线的距离可得出点Q到直线AC的距离是线段QF的长度,
⑧根据点到直线的距离可得出点P到直线AB的距离是线段PE的长度,
故答案为PQ,QD,QF,PE.
20.【解答】解:如图所示
(1)沿AB走,两点之间线段最短;
(2)沿AC走,垂线段最短;
(3)沿BD走,垂线段最短.
_21?????????è?????(www.21cnjy.com)_
2021年七年级数学下册课时训练:5.1《相交线》
班级__________姓名__________学号__________
一.选择题(共7小题)
1.如图图形中,∠1与∠2是对顶角的有( )
A.B.C.D.
2.如图,∠B的内错角是( )
A.∠1 B.∠2 C.∠3 D.∠4
3.平面内三条两两相交的直线( )
A.有一个交点 B.有一个或三个交点
C.有三个交点 D.上述都不对
4.如图,点O在直线AB上,CO⊥AB,若∠COD=52°,则∠AOD的度数是( )
A.38° B.128° C.142° D.150°
5.如图,把河AB中的水引到C,拟修水渠中最短的是( )
A.CM B.CN C.CP D.CQ
6.下列所示的四个图形中,∠1和∠2是同位角的是( )
A.②③ B.①②③ C.③④ D.①②④
7.∠1的对顶角是∠2,∠2的邻补角是∠3,若∠3=50°,则∠1的度数是( )
A.40° B.50° C.130° D.50°或130°
二.填空题(共7小题)
8.从直线外一点到这条直线的 ,叫做该点到直线的距离.
9.如图,与∠1是同旁内角的是 ,与∠2是内错角的是 .
10.如图,AH⊥BC,垂足为H,若AB=1.7cm,AC=2cm,AH=1.2cm,则点A到直线BC的距离是 ________cm.
11.如图,两直线交于点O,若∠1+∠2=76°,则∠1= 度.
12.若∠1=64°,则∠1的邻补角度数为 .
13.如图所示的图形中,同位角有 对.
14.如图,直线a、b相交,∠1=36°,则∠2﹣∠3= .
三.解答题(共6小题)
15.如图,有两堵围墙,有人想测量地面上两堵围墙内所形成的∠AOB的度数,但人又不能进入围墙,只能站在墙外,请问该如何测量?
16.如图,请分别写出各图中的一对同位角、内错角和同旁内角.
17.如图,找出标注角中的同位角、内错角和同旁内角.
18.如图,直线AB,CD相交于O,OE是∠AOD的平分线,∠AOC=28°,求∠AOE的度数.
19.如图,
①过点Q作QD⊥AB,垂足为D,
②过点P作PE⊥AB,垂足为E,
③过点Q作QF⊥AC,垂足为F,
④连接P、Q两点,
⑤P、Q两点间的距离是线段 的长度,
⑥点Q到直线AB的距离是线段 的长度,
⑦点Q到直线AC的距离是线段 的长度,
⑧点P到直线AB的距离是线段 的长度.
20.如图所示,码头、火车站分别位于A,B两点,直线a和b分别表示铁路与河流.
(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
参考答案
一.选择题(共7小题)
1.【解答】解:B、C、D选项中的∠1与∠2都不是对顶角,
A选项中的∠1与∠2都是对顶角,
故选:A.
2.【解答】解:A、∠B的内错角是∠1,故此选项符合题意;
B、∠B与∠2是同旁内角,故此选项不合题意;
C、∠B与∠3是同位角,故此选项不合题意;
D、∠B与∠4是不是内错角,故此选项不合题意;
故选:A.
3.【解答】解:如图,
三条直线两两相交时,共有3个交点;三条直线相交于一点时,有一个交点.
故选:B.
4.【解答】解:如图所示:∵CO⊥AB,
∴∠AOC=90°,
∵∠COD=52°,
∴∠AOD=∠AOC+∠COD=90°+52°=142°.
故选:C.
5.【解答】解:如图,CP⊥AB,垂足为P,
在P处开水渠,则水渠最短.
因为直线外一点与直线上各点连线的所有线段中,垂线段最短.
故选:C.
6.【解答】解:图①②④中,∠1和∠2是同位角,
故选:D.
7.【解答】解:∵∠2的邻补角是∠3,∠3=50°,
∴∠2=130°,
∵∠1的对顶角是∠2,
∴∠1=130°,
故选:C.
二.填空题(共7小题)
8.【解答】解:从直线外一点到这条直线的垂线段的长度,叫做该点到直线的距离.
故答案为:垂线段的长度.
9.【解答】解:如图,与∠1是同旁内角的是∠5,与∠2是内错角的是∠3.
故答案为:∠5;∠3.
10.【解答】解:∵AH⊥BC,AH=1.2cm,
∴点A到直线BC的距离是1.2cm,
故答案为:1.2.
11.【解答】解:∵两直线交于点O,
∴∠1=∠2,
∵∠1+∠2=76°,
∴∠1=38°.
故答案为:38.
12.【解答】解:∵∠1=64°,
∴∠1的邻补角度数为:180°﹣64°=116°.
故答案为:116°.
13.【解答】解:如图:
∠CAG的同位角是∠DBG,∠EAG的同位角是∠FBG,
∴图中同位角有2对.
故答案为:2.
14.【解答】解:∵直线a、b相交,∠1=36°,
∴∠3=∠1=36°,∠2=180°﹣∠1=144°,
∴∠2﹣∠3=144°﹣36°=108°.
故答案为:108°.
三.解答题(共6小题)
15.【解答】解:如图,延长AO,先测量出∠BOC的度数,然后根据∠AOB与∠BOC是邻补角即可求解,
∠AOB=180°﹣∠BOC.
16.【解答】解:同位角是∠ADF与∠ABC,∠EDF与∠BCD,
内错角是∠EDB与∠DBC,∠ABC与∠BCD,
同旁内角是∠FDB与∠DBC,∠BCD与∠CDE.
17.【解答】解:同位角有∠4与∠8、∠4与∠7、∠2与∠3;
内错角有∠1与∠3、∠7与∠6、∠6与∠8;
同旁内角有∠1与∠4、∠3与∠8,∠1与∠7.
18.【解答】解:∵∠AOC+∠AOD=180°,∠AOC=28°,
∴∠AOD=152°.
∵OE平分∠AOD,
∴∠AOE=∠AOD=76°.
19.【解答】解:①②③④作图如图所示:
⑤根据两点之间距离即可得出P、Q两点间的距离是线段PQ的长度,
⑥根据点到直线的距离可得出点Q到直线AB的距离是线段QD的长度,
⑦根据点到直线的距离可得出点Q到直线AC的距离是线段QF的长度,
⑧根据点到直线的距离可得出点P到直线AB的距离是线段PE的长度,
故答案为PQ,QD,QF,PE.
20.【解答】解:如图所示
(1)沿AB走,两点之间线段最短;
(2)沿AC走,垂线段最短;
(3)沿BD走,垂线段最短.
_21?????????è?????(www.21cnjy.com)_
