五年级数学下册课件-探索图形 -人教版(共64张PPT)
文档属性
| 名称 | 五年级数学下册课件-探索图形 -人教版(共64张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 8.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-16 11:44:51 | ||
图片预览




文档简介
(共64张PPT)
探索图形
正方体
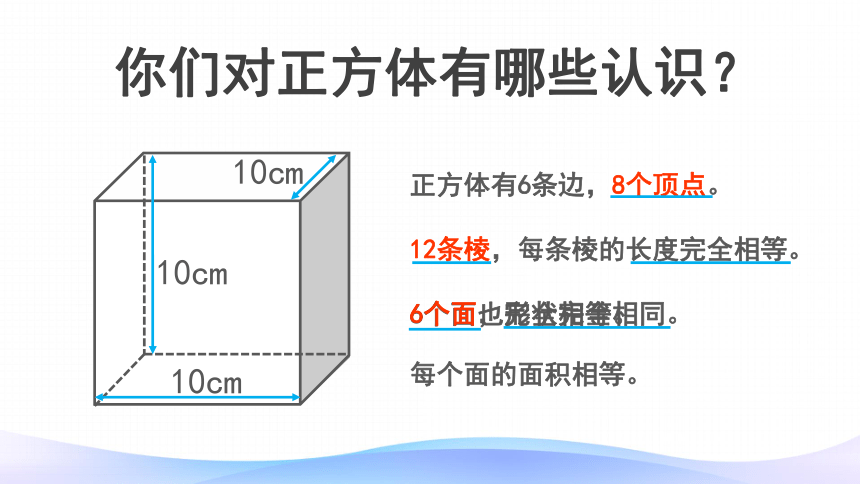
你们对正方体有哪些认识?
正方体有6条边,8个顶点。
12条棱,每条棱的长度完全相等。
6个面也完全相等。
6个面,形状完全相同。
每个面的面积相等。
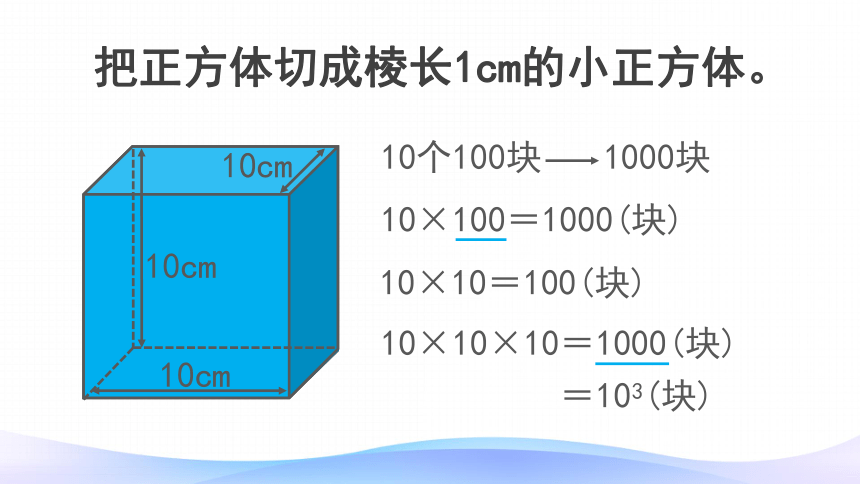
10cm
10cm
10cm
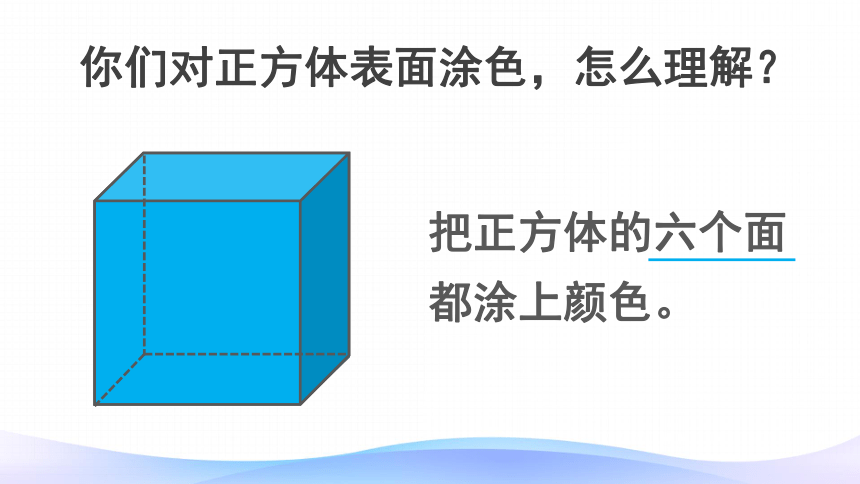
把正方体的六个面
都涂上颜色。
你们对正方体表面涂色,怎么理解?
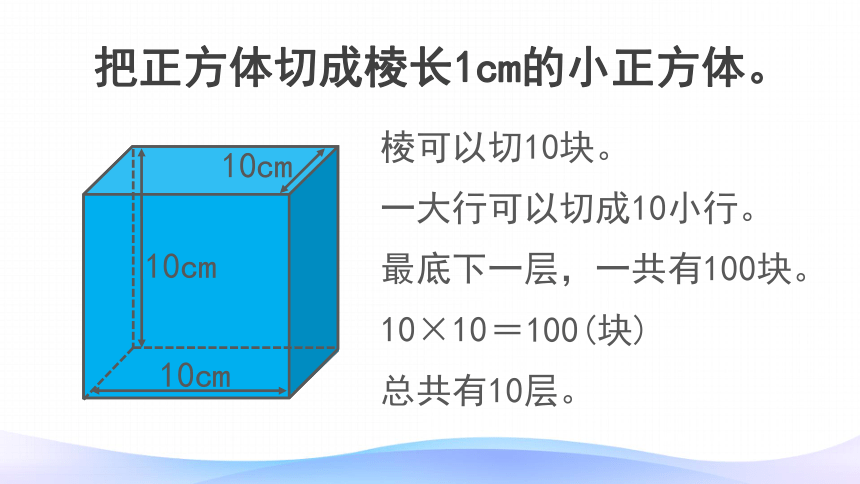
把正方体切成棱长1cm的小正方体。
10cm
10cm
10cm
棱可以切10块。
一大行可以切成10小行。
最底下一层,一共有100块。
10×10
=100(块)
总共有10层。
把正方体切成棱长1cm的小正方体。
10cm
10cm
10cm
10个100块
1000块
10×100=1000(块)
10×10×10=1000(块)
=103(块)
10×10=100(块)
1000块小正方体的涂色面数,相同吗?
分为四类:
第一类是没有涂颜色的;
第二类是只涂一面颜色的;
第三类是涂两面颜色的;
第四类是涂三面颜色的。
四类小正方体,各有多少块?
从简单的来探索,从简单的图形里面找到规律。
利用规律,解决
复杂问题。
探索图形
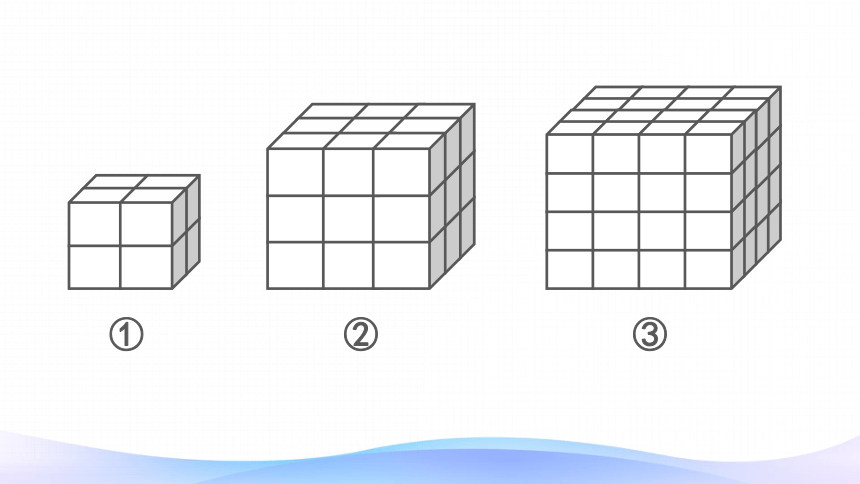
①
②
③
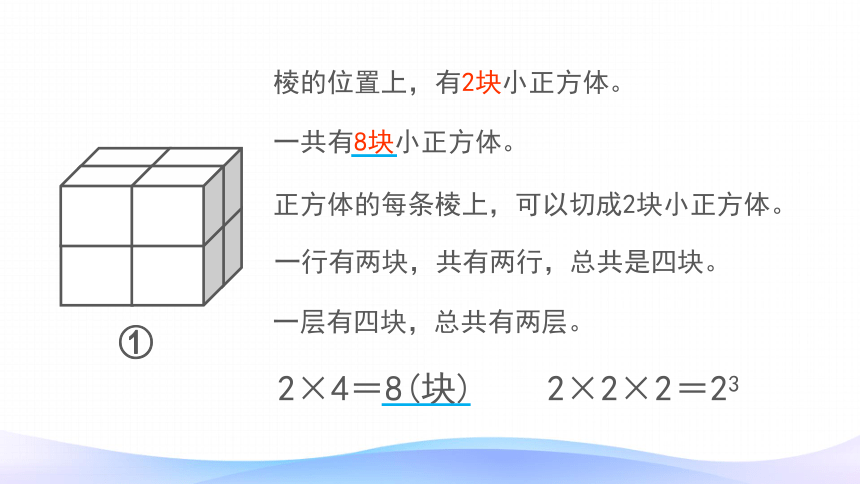
棱的位置上,有2块小正方体。
①
一共有8块小正方体。
正方体的每条棱上,可以切成2块小正方体。
一行有两块,共有两行,总共是四块。
一层有四块,总共有两层。
2×4=8(块)
2×2×2
=23
②
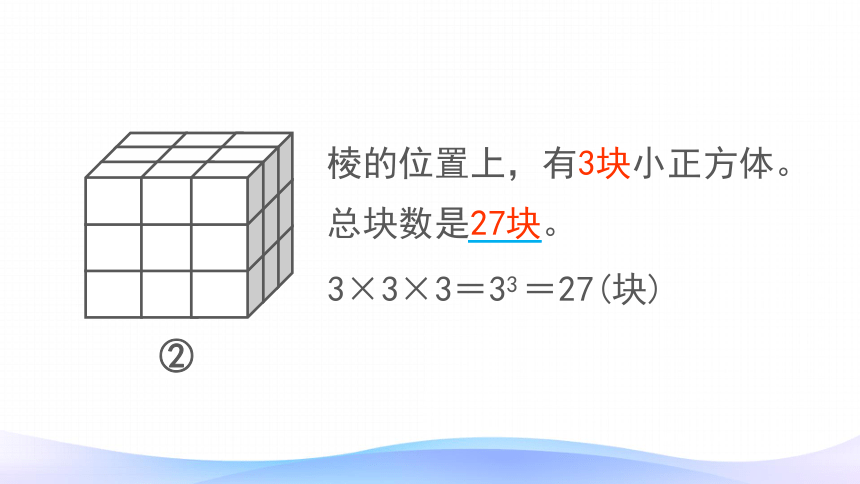
棱的位置上,有3块小正方体。
总块数是27块。
3×3×3=33
=27(块)
③
棱的位置上,有4块小正方体。
总块数是64块。
4×4×4=43=64(块)
涂红颜色的小正方体,有3个面涂上颜色。
棱的位置上,有3块小正方体。
因为其他的三个面,都在里面。
它们没有露在大正方体的表面。
所以,其他三个面没有涂上颜色。
三面涂色的小正方体,一共有8块。
①
②
③
④
三面涂色的小正方体,一共有8块。
⑥
⑤
⑧
⑦
涂黄颜色的小正方体,有2个面涂上颜色。
两面涂色的小正方体,一共有12块。
2
1
3
4
5
6
7
8
9
6
2
3
1
4
8
9
1
1
1
0
涂黄颜色的小正方体,有2个面涂上颜色。
两面涂色的小正方体,一共有12块。
2
3
1
4
1
1
1
0
12
7
涂黄颜色的小正方体,有2个面涂上颜色。
两面涂色的小正方体,一共有12块。
2
1
3
4
5
6
7
8
9
涂黄颜色的小正方体,有2个面涂上颜色。
两面涂色的小正方体,一共有12块。
6
2
3
1
4
8
9
1
1
1
0
涂黄颜色的小正方体,有2个面涂上颜色。
两面涂色的小正方体,一共有12块。
2
3
1
4
1
1
1
0
12
7
涂黄颜色的小正方体,有2个面涂上颜色。
两面涂色的小正方体,一共有12块。
因为每一个两面涂色的正方体它都在每一条个棱上。
这个正方体,一共有十二条棱,每条棱上有一个小正方体。
1×12=12(块)
两面涂色的小正方体,一共有12块。
一条棱上,有一块小正方体。
大正方体,一共12条棱。
涂蓝颜色的小正方体,有1个面涂上颜色。
一面涂色的小正方体,一共有6块。
1
2
3
3
4
5
涂蓝颜色的小正方体,有1个面涂上颜色。
一面涂色的小正方体,一共有6块。
6
4
5
涂蓝颜色的小正方体,有1个面涂上颜色。
一面涂色的小正方体,一共有6块。
三面涂色的8块,两面涂色的12块。
8+12
=20(块)
20+6
=26(块)
27块
我们算的只是表面涂色的正
方体的块数。实际上,大正
方体里面,还有一个,6个
面都没有露出来的正方体。
因为它的6个面,都有小正方体挡住了。
一个面都没有涂上颜色的小正方体,有一块。
①
②
③
活动要求
1、用小正方体学具,分别摆出上图中相应的大正方体。
2、如果在每个大正方体的表面涂上颜色,请把每类小正方体的块数,填在第一题的表格里。
3、观察每类小正方体,都在大正方体的什么位置?完成体验单上的第二题。
图形
棱上的
块数
总块数
三面涂色
的块数
二面涂色
的块数
一面涂色
的块数
没有面涂
色的块数
①
2
8
8
0
0
0
②
3
27
③
4
64
探索图形
8
12
6
1
8
24
(4-2)×12
4是每条棱上小正方体的块数。
减2,是减掉顶点处的两个三面涂色的小正方体。
因为一条棱上有两个小正方体,一个正方体一共有12条棱。
=24(块)
两面涂色的块数,是多少?
图形
棱上的
块数
总块数
三面涂色
的块数
二面涂色
的块数
一面涂色
的块数
没有面涂
色的块数
①
2
8
8
0
0
0
②
3
27
③
4
64
8
12
6
1
8
24
24
探索图形
(4-2)2×6
一面涂色的块数,是多少?
4表示的是一条棱上小正方体的块数。
减2,是这条棱上两面涂色的小正方体的块数。
平方是算出它这个面上一共有4个小正方体。
两层是4减2的差,相乘的。
(4-2)2×6
=24(块)
一面涂色的块数,是多少?
每个面上有四块一面涂色的小正方体。
图形
棱上的
块数
总块数
三面涂色
的块数
二面涂色
的块数
一面涂色
的块数
没有面涂
色的块数
①
②
③
4
64
8
24
24
8
探索图形
2
8
8
0
0
0
3
27
8
12
6
1
(4-2)3
=8(块)
没有面涂色的块数,是多少?
4减2,是每条棱上小正方体的块数。
2是一面涂色的小正方体的块数。
V=a3
小正方体的棱长是2。
没有面涂色的块数,是多少?
先算出,大正方体的总块数是64块。
然后,我们也知道了三面,两面,还有一
面的块数。拿总块数减去三面、两面和一
面的块数。最后,就等于没有涂色的块数。
没有面涂色的块数,是多少?
(4-2)3
=8(块)
64-8-24-24
=8(块)
你们发现有什么规律?
三面涂色的小正方体,都在大正方体的棱角的位置。
三条棱相会的顶点。
两面涂色的小正方体,都在大正方体的每条棱中间。
没有涂色的小正方体,都在大正方体的最中心位置。
没有涂色的小正方体,都在大正方体的核心位置。
你们发现有什么规律?
一面涂色的小正方体,都在大正方体每个面的中心。
12×2
数出每条棱总共有多少个小正方体,
减去两头是三面涂色的小正方体,剩下的
就是两面涂色的小正方体。
=24(块)
怎么计算两面涂色的块数?
用每条棱上的块数,减去两面涂色的块数,然后剩下的就是一面涂色的块数。
S=a×a
用每条棱上的块数,减去两面涂色的块数,算出差的平方,再乘每条棱上的块数。
因为正方体有6个面,再乘6。
怎么计算一面涂色的块数?
用每条棱上小正方体的块数,减2的差的平方,
再乘6。
怎么计算一面涂色的块数?
怎么计算没有面涂色的块数?
用总块数减去,三面涂色的块数、两面涂色的块数和一面涂色的块数。
怎么计算没有面涂色的块数?
用每条棱上的块数,减去它每条棱上的两面的块数,
再乘这个差的立方。
怎么计算没有面涂色的块数?
先用每条棱上小正方体的块数,减
去一面涂色的块数,就是组成的较小的
正方体的棱长。然后,用棱长的立方,
就算出来这个小正方体的块数。
④
探索图形
图形
棱上的
块数
总块数
三面涂色
的块数
二面涂色
的块数
一面涂色
的块数
没有面涂
色的块数
①
②
③
4
64
8
24
24
8
④
5
125
⑤
6
216
2
8
8
0
0
0
3
27
8
12
6
1
④
⑤
探索图形
图形
棱上的
块数
总块数
三面涂色
的块数
二面涂色
的块数
一面涂色
的块数
没有面涂
色的块数
①
②
③
4
64
8
24
24
8
④
5
125
8
36
54
27
⑤
6
216
8
48
96
64
2
8
8
0
0
0
3
27
8
12
6
1
(1)三面涂色的块数:
1×8
(2)二面涂色的块数:
(10-2)×12
(3)一面涂色的块数:
(10-2)2×6
10cm
10cm
10cm
=8(块)
=96(块)
=384(块)
(4)没有面涂色的块数:
(10-2)3
10cm
10cm
10cm
=512(块)
1000-8-96-384=512(块)
10×10×10=103
10cm
10cm
10cm
化繁为简
通过简单图形我们找到规律,再来解决问题。
探索图形
图形
棱上的
块数
总块数
三面涂色
的块数
二面涂色
的块数
一面涂色
的块数
没有面涂
色的块数
①
②
③
4
64
8
24
24
8
④
5
125
8
36
54
27
⑤
6
216
8
48
96
64
……
……
……
……
……
……
n
n3
(n-2)×12
(n-2)2×6
(n-2)3
8
2
8
8
0
0
0
3
27
8
12
6
1
怎么算正方体:
如果把正方体表面涂上颜色,怎么算它的总
块数,怎么算它的三面涂色的块数,怎么算它两
面涂色的块数,怎么算它一面涂色的块数,怎么
算它没有面涂色的块数。
化繁为简法。
无论是大或者是小的正方体,它的三面涂色
的块数,一定是8块。
三面涂色的是1乘8。每个正方体都是8块。因为它是在每个正方体的顶点位置,都有八个顶点。
通过分小组合作,共同探究,运用了化繁为简的方法。
发现了小正方体涂色块数的规律。
应用规律快速地解决了复杂的问题。
作业布置
如果摆成下面的几何体,你会数出小正方体的块数吗?
(
)块
(
)块
(
)块
再见!
探索图形
正方体
你们对正方体有哪些认识?
正方体有6条边,8个顶点。
12条棱,每条棱的长度完全相等。
6个面也完全相等。
6个面,形状完全相同。
每个面的面积相等。
10cm
10cm
10cm
把正方体的六个面
都涂上颜色。
你们对正方体表面涂色,怎么理解?
把正方体切成棱长1cm的小正方体。
10cm
10cm
10cm
棱可以切10块。
一大行可以切成10小行。
最底下一层,一共有100块。
10×10
=100(块)
总共有10层。
把正方体切成棱长1cm的小正方体。
10cm
10cm
10cm
10个100块
1000块
10×100=1000(块)
10×10×10=1000(块)
=103(块)
10×10=100(块)
1000块小正方体的涂色面数,相同吗?
分为四类:
第一类是没有涂颜色的;
第二类是只涂一面颜色的;
第三类是涂两面颜色的;
第四类是涂三面颜色的。
四类小正方体,各有多少块?
从简单的来探索,从简单的图形里面找到规律。
利用规律,解决
复杂问题。
探索图形
①
②
③
棱的位置上,有2块小正方体。
①
一共有8块小正方体。
正方体的每条棱上,可以切成2块小正方体。
一行有两块,共有两行,总共是四块。
一层有四块,总共有两层。
2×4=8(块)
2×2×2
=23
②
棱的位置上,有3块小正方体。
总块数是27块。
3×3×3=33
=27(块)
③
棱的位置上,有4块小正方体。
总块数是64块。
4×4×4=43=64(块)
涂红颜色的小正方体,有3个面涂上颜色。
棱的位置上,有3块小正方体。
因为其他的三个面,都在里面。
它们没有露在大正方体的表面。
所以,其他三个面没有涂上颜色。
三面涂色的小正方体,一共有8块。
①
②
③
④
三面涂色的小正方体,一共有8块。
⑥
⑤
⑧
⑦
涂黄颜色的小正方体,有2个面涂上颜色。
两面涂色的小正方体,一共有12块。
2
1
3
4
5
6
7
8
9
6
2
3
1
4
8
9
1
1
1
0
涂黄颜色的小正方体,有2个面涂上颜色。
两面涂色的小正方体,一共有12块。
2
3
1
4
1
1
1
0
12
7
涂黄颜色的小正方体,有2个面涂上颜色。
两面涂色的小正方体,一共有12块。
2
1
3
4
5
6
7
8
9
涂黄颜色的小正方体,有2个面涂上颜色。
两面涂色的小正方体,一共有12块。
6
2
3
1
4
8
9
1
1
1
0
涂黄颜色的小正方体,有2个面涂上颜色。
两面涂色的小正方体,一共有12块。
2
3
1
4
1
1
1
0
12
7
涂黄颜色的小正方体,有2个面涂上颜色。
两面涂色的小正方体,一共有12块。
因为每一个两面涂色的正方体它都在每一条个棱上。
这个正方体,一共有十二条棱,每条棱上有一个小正方体。
1×12=12(块)
两面涂色的小正方体,一共有12块。
一条棱上,有一块小正方体。
大正方体,一共12条棱。
涂蓝颜色的小正方体,有1个面涂上颜色。
一面涂色的小正方体,一共有6块。
1
2
3
3
4
5
涂蓝颜色的小正方体,有1个面涂上颜色。
一面涂色的小正方体,一共有6块。
6
4
5
涂蓝颜色的小正方体,有1个面涂上颜色。
一面涂色的小正方体,一共有6块。
三面涂色的8块,两面涂色的12块。
8+12
=20(块)
20+6
=26(块)
27块
我们算的只是表面涂色的正
方体的块数。实际上,大正
方体里面,还有一个,6个
面都没有露出来的正方体。
因为它的6个面,都有小正方体挡住了。
一个面都没有涂上颜色的小正方体,有一块。
①
②
③
活动要求
1、用小正方体学具,分别摆出上图中相应的大正方体。
2、如果在每个大正方体的表面涂上颜色,请把每类小正方体的块数,填在第一题的表格里。
3、观察每类小正方体,都在大正方体的什么位置?完成体验单上的第二题。
图形
棱上的
块数
总块数
三面涂色
的块数
二面涂色
的块数
一面涂色
的块数
没有面涂
色的块数
①
2
8
8
0
0
0
②
3
27
③
4
64
探索图形
8
12
6
1
8
24
(4-2)×12
4是每条棱上小正方体的块数。
减2,是减掉顶点处的两个三面涂色的小正方体。
因为一条棱上有两个小正方体,一个正方体一共有12条棱。
=24(块)
两面涂色的块数,是多少?
图形
棱上的
块数
总块数
三面涂色
的块数
二面涂色
的块数
一面涂色
的块数
没有面涂
色的块数
①
2
8
8
0
0
0
②
3
27
③
4
64
8
12
6
1
8
24
24
探索图形
(4-2)2×6
一面涂色的块数,是多少?
4表示的是一条棱上小正方体的块数。
减2,是这条棱上两面涂色的小正方体的块数。
平方是算出它这个面上一共有4个小正方体。
两层是4减2的差,相乘的。
(4-2)2×6
=24(块)
一面涂色的块数,是多少?
每个面上有四块一面涂色的小正方体。
图形
棱上的
块数
总块数
三面涂色
的块数
二面涂色
的块数
一面涂色
的块数
没有面涂
色的块数
①
②
③
4
64
8
24
24
8
探索图形
2
8
8
0
0
0
3
27
8
12
6
1
(4-2)3
=8(块)
没有面涂色的块数,是多少?
4减2,是每条棱上小正方体的块数。
2是一面涂色的小正方体的块数。
V=a3
小正方体的棱长是2。
没有面涂色的块数,是多少?
先算出,大正方体的总块数是64块。
然后,我们也知道了三面,两面,还有一
面的块数。拿总块数减去三面、两面和一
面的块数。最后,就等于没有涂色的块数。
没有面涂色的块数,是多少?
(4-2)3
=8(块)
64-8-24-24
=8(块)
你们发现有什么规律?
三面涂色的小正方体,都在大正方体的棱角的位置。
三条棱相会的顶点。
两面涂色的小正方体,都在大正方体的每条棱中间。
没有涂色的小正方体,都在大正方体的最中心位置。
没有涂色的小正方体,都在大正方体的核心位置。
你们发现有什么规律?
一面涂色的小正方体,都在大正方体每个面的中心。
12×2
数出每条棱总共有多少个小正方体,
减去两头是三面涂色的小正方体,剩下的
就是两面涂色的小正方体。
=24(块)
怎么计算两面涂色的块数?
用每条棱上的块数,减去两面涂色的块数,然后剩下的就是一面涂色的块数。
S=a×a
用每条棱上的块数,减去两面涂色的块数,算出差的平方,再乘每条棱上的块数。
因为正方体有6个面,再乘6。
怎么计算一面涂色的块数?
用每条棱上小正方体的块数,减2的差的平方,
再乘6。
怎么计算一面涂色的块数?
怎么计算没有面涂色的块数?
用总块数减去,三面涂色的块数、两面涂色的块数和一面涂色的块数。
怎么计算没有面涂色的块数?
用每条棱上的块数,减去它每条棱上的两面的块数,
再乘这个差的立方。
怎么计算没有面涂色的块数?
先用每条棱上小正方体的块数,减
去一面涂色的块数,就是组成的较小的
正方体的棱长。然后,用棱长的立方,
就算出来这个小正方体的块数。
④
探索图形
图形
棱上的
块数
总块数
三面涂色
的块数
二面涂色
的块数
一面涂色
的块数
没有面涂
色的块数
①
②
③
4
64
8
24
24
8
④
5
125
⑤
6
216
2
8
8
0
0
0
3
27
8
12
6
1
④
⑤
探索图形
图形
棱上的
块数
总块数
三面涂色
的块数
二面涂色
的块数
一面涂色
的块数
没有面涂
色的块数
①
②
③
4
64
8
24
24
8
④
5
125
8
36
54
27
⑤
6
216
8
48
96
64
2
8
8
0
0
0
3
27
8
12
6
1
(1)三面涂色的块数:
1×8
(2)二面涂色的块数:
(10-2)×12
(3)一面涂色的块数:
(10-2)2×6
10cm
10cm
10cm
=8(块)
=96(块)
=384(块)
(4)没有面涂色的块数:
(10-2)3
10cm
10cm
10cm
=512(块)
1000-8-96-384=512(块)
10×10×10=103
10cm
10cm
10cm
化繁为简
通过简单图形我们找到规律,再来解决问题。
探索图形
图形
棱上的
块数
总块数
三面涂色
的块数
二面涂色
的块数
一面涂色
的块数
没有面涂
色的块数
①
②
③
4
64
8
24
24
8
④
5
125
8
36
54
27
⑤
6
216
8
48
96
64
……
……
……
……
……
……
n
n3
(n-2)×12
(n-2)2×6
(n-2)3
8
2
8
8
0
0
0
3
27
8
12
6
1
怎么算正方体:
如果把正方体表面涂上颜色,怎么算它的总
块数,怎么算它的三面涂色的块数,怎么算它两
面涂色的块数,怎么算它一面涂色的块数,怎么
算它没有面涂色的块数。
化繁为简法。
无论是大或者是小的正方体,它的三面涂色
的块数,一定是8块。
三面涂色的是1乘8。每个正方体都是8块。因为它是在每个正方体的顶点位置,都有八个顶点。
通过分小组合作,共同探究,运用了化繁为简的方法。
发现了小正方体涂色块数的规律。
应用规律快速地解决了复杂的问题。
作业布置
如果摆成下面的几何体,你会数出小正方体的块数吗?
(
)块
(
)块
(
)块
再见!
