北师大版数学七年级下册1.2 幂的乘方与积的乘方——幂的乘方 课件(第一课时 20张)
文档属性
| 名称 | 北师大版数学七年级下册1.2 幂的乘方与积的乘方——幂的乘方 课件(第一课时 20张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 758.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-16 09:46:43 | ||
图片预览






文档简介
第一章 整式的乘除
2 幂的乘方与积的乘方
课时1 幂的乘方
1.了解幂的乘方的运算法则,熟练运用幂的乘方的运算法则进行实际计算.(重点)
2.掌握幂的乘方的运算法则的推导.(难点)
3.体会数式通性和从具体到抽象的思想方法在研究数学问题中的作用.
学习目标
新课导入
思 考
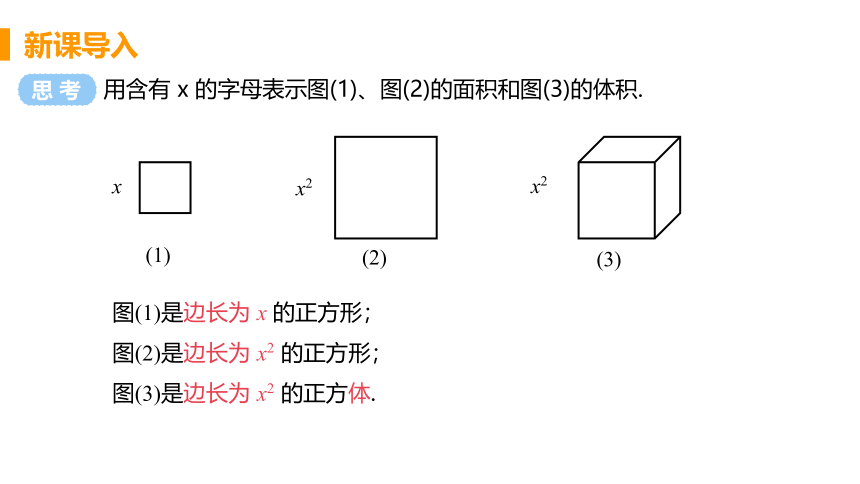
用含有 x 的字母表示图(1)、图(2)的面积和图(3)的体积.
图(1)是边长为 x 的正方形;
图(2)是边长为 x2 的正方形;
图(3)是边长为 x2 的正方体.
x
(1)
(2)
x2
x2
(3)
新课导入
思 考
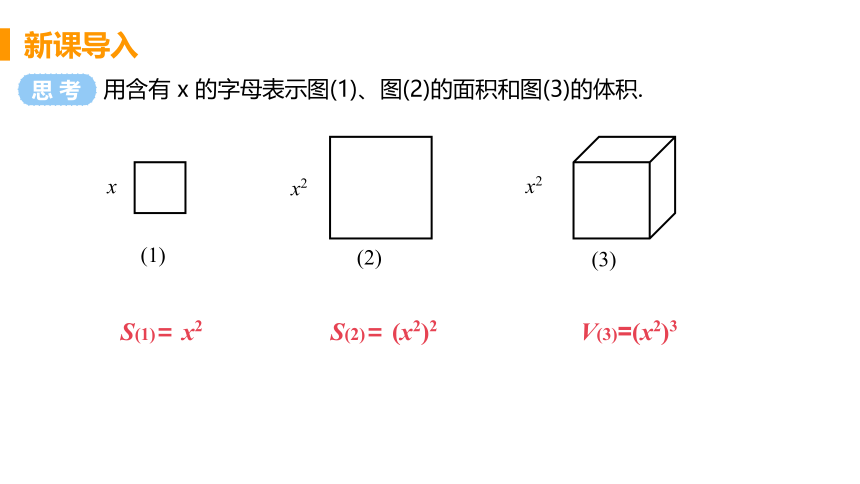
用含有 x 的字母表示图(1)、图(2)的面积和图(3)的体积.
S(1)= x2
x
(1)
(2)
x2
x2
(3)
S(2)= (x2)2
V(3)=(x2)3
新课导入
(1) (x2)2 = x2?2= x4 ;
(2) (x2)3 = x2?3= x6 .
观察计算结果,你能发现什么规律?
(1) (x2)2 = x2?x2 = x2+2= x4 ;
(2) (x2)3 = x2?x2?x2 = x2+2+2= x6 .
结 论
新课导入
观察计算结果,你能发现什么规律?(m,n为正整数)
(1) (32)3=32×32×32=36 ;
(2) (a2)3=a2×a2×a2=a6 ;
(3) (am)3=am×am×am=a3m (m是正整数);
(4) (am)n=am×am×???am=amn (m,n为正整数).
n个am
新课导入
规 律
以上4个式子都是幂的乘方的形式,根据已经学过的乘方的意义和同底数幂的乘法性质可以得出幂的乘方的结果中底数不变,指数为两个指数的乘积(其中指数均为正整数).
思考:你能总结出幂的乘方的运算法则吗?
新课讲解
知识点1 幂的乘方
性质:幂的乘方,底数不变,指数相乘.
n个m
n个am
符号表示:(am)n=amn(m,n都是正整数).
一般地,对于任意底数a与任意正整数m,n.
(am)n=am×am×???am=amn
=a(m+m+m+???+m)
新课讲解
知识点1 幂的乘方
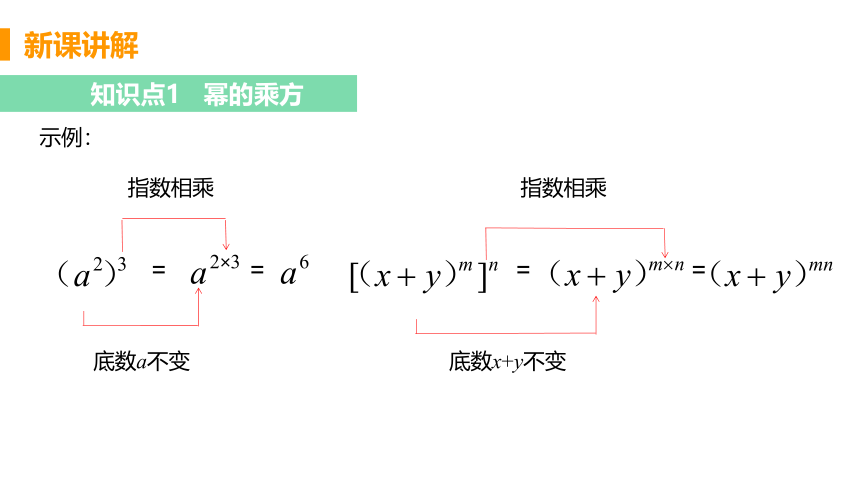
示例:
= = = =
底数a不变
指数相乘
底数x+y不变
指数相乘
新课讲解
(1) 幂的乘方的性质也可以推广为 [(am)n]p=amnp
(m,n,p都为正整数).
(2) 幂的乘方的性质可以逆用,即 amn=(am)n (m,n为正整数).
知识点1 幂的乘方
新课讲解
(1)在形式上,幂的乘方的底数本身就是一个幂,根据乘方的意义和同底数幂的乘法的性质可以推出幂的乘方的性质;
(2)在幂的乘方中,底数可以是单项式,也可以是多项式.
幂的乘方用性质,
底数不变指数乘,
推广指数一次幂,
逆用性质巧计算.
知识点1 幂的乘方
新课讲解
练一练
1
计算下列式子:
(1) (103)5 ; (2) (a4)4 ;
(3) (am)2 ; (4) -(x4)3 .
解:(1) (103)5=103×5=1015 ;
(2) (a4)4 =a4×4=a16 ;
(3) (am)2 = am×2= a2m ;
(4) -(x4)3=-x4×3=-x12 .
新课讲解
练一练
2
(3) -[(a-b)3 ]4 = -(a-b)3×4= -(a-b)12 .
计算:(1) (an+1)2 ; (2) [(-x)7]4 ; (3) -[(a-b)3 ]4 .
解:(1) (an+1)2 = a(n+1)×2 = a2n+2 ;
(2) [(-x)7]4 = (-x)7×4 = (-x)28= x28 ;
新课讲解
练一练
3
已知 a2n=3,求 a4n-a6n 的值.
解:a4n-a6n = (a2n)2- (a2n)3
= 32-33
= -18 .
把指数是积的形式的幂写成幂的乘方,amn=(am)n
(m,n都是正整数),然后整体代入,求出式子的值.
课堂小结
幂的乘方
(am)n=amn (m,n为正整数)
性质:幂的乘方,底数不变,指数相乘.
当堂小练
1.计算(x3)3的结果是( )
A. x5 B. x6 C. x8 D. x9
D
2. 下列运算正确的是( )
A. a2·a3=a6 B. (a2)3=a6
C. a5·a5=a25 D. (3x)3=3x3
B
a5
a10
27x3
当堂小练
3. (1)若2x+y=3,则4x·2y= .
(2)已知3m·9m·27m·81m=330,求m的值.
8
解:3m·32m·33m·34m=330
310m=330
m=3
拓展与延伸
已知16m=4×22n-2,27n=9×3m+3 ,求 m,n 的值.
解:因为16m=4×22n-2,所以24m =22×22n-2 .
所以24m=22n,即4m=2n,2m=n. ①
因为 27n=9×3m+3 ,所以(33)n=32×3m+3 .
所以33n=3m+5,即3n=m+5. ②
由①②得,m=1,n=2.
拓展与延伸
比较 355、444 、533 的大小.
解: 355 = (35)11 = 24311 , 444 = (44)11 = 25611 ,
533 = (53)11 = 12511 .
因为125<243<256,则12511<24311<25611 .
所以 533<355< 444 .
布置作业
请完成P68对应习题
2 幂的乘方与积的乘方
课时1 幂的乘方
1.了解幂的乘方的运算法则,熟练运用幂的乘方的运算法则进行实际计算.(重点)
2.掌握幂的乘方的运算法则的推导.(难点)
3.体会数式通性和从具体到抽象的思想方法在研究数学问题中的作用.
学习目标
新课导入
思 考
用含有 x 的字母表示图(1)、图(2)的面积和图(3)的体积.
图(1)是边长为 x 的正方形;
图(2)是边长为 x2 的正方形;
图(3)是边长为 x2 的正方体.
x
(1)
(2)
x2
x2
(3)
新课导入
思 考
用含有 x 的字母表示图(1)、图(2)的面积和图(3)的体积.
S(1)= x2
x
(1)
(2)
x2
x2
(3)
S(2)= (x2)2
V(3)=(x2)3
新课导入
(1) (x2)2 = x2?2= x4 ;
(2) (x2)3 = x2?3= x6 .
观察计算结果,你能发现什么规律?
(1) (x2)2 = x2?x2 = x2+2= x4 ;
(2) (x2)3 = x2?x2?x2 = x2+2+2= x6 .
结 论
新课导入
观察计算结果,你能发现什么规律?(m,n为正整数)
(1) (32)3=32×32×32=36 ;
(2) (a2)3=a2×a2×a2=a6 ;
(3) (am)3=am×am×am=a3m (m是正整数);
(4) (am)n=am×am×???am=amn (m,n为正整数).
n个am
新课导入
规 律
以上4个式子都是幂的乘方的形式,根据已经学过的乘方的意义和同底数幂的乘法性质可以得出幂的乘方的结果中底数不变,指数为两个指数的乘积(其中指数均为正整数).
思考:你能总结出幂的乘方的运算法则吗?
新课讲解
知识点1 幂的乘方
性质:幂的乘方,底数不变,指数相乘.
n个m
n个am
符号表示:(am)n=amn(m,n都是正整数).
一般地,对于任意底数a与任意正整数m,n.
(am)n=am×am×???am=amn
=a(m+m+m+???+m)
新课讲解
知识点1 幂的乘方
示例:
= = = =
底数a不变
指数相乘
底数x+y不变
指数相乘
新课讲解
(1) 幂的乘方的性质也可以推广为 [(am)n]p=amnp
(m,n,p都为正整数).
(2) 幂的乘方的性质可以逆用,即 amn=(am)n (m,n为正整数).
知识点1 幂的乘方
新课讲解
(1)在形式上,幂的乘方的底数本身就是一个幂,根据乘方的意义和同底数幂的乘法的性质可以推出幂的乘方的性质;
(2)在幂的乘方中,底数可以是单项式,也可以是多项式.
幂的乘方用性质,
底数不变指数乘,
推广指数一次幂,
逆用性质巧计算.
知识点1 幂的乘方
新课讲解
练一练
1
计算下列式子:
(1) (103)5 ; (2) (a4)4 ;
(3) (am)2 ; (4) -(x4)3 .
解:(1) (103)5=103×5=1015 ;
(2) (a4)4 =a4×4=a16 ;
(3) (am)2 = am×2= a2m ;
(4) -(x4)3=-x4×3=-x12 .
新课讲解
练一练
2
(3) -[(a-b)3 ]4 = -(a-b)3×4= -(a-b)12 .
计算:(1) (an+1)2 ; (2) [(-x)7]4 ; (3) -[(a-b)3 ]4 .
解:(1) (an+1)2 = a(n+1)×2 = a2n+2 ;
(2) [(-x)7]4 = (-x)7×4 = (-x)28= x28 ;
新课讲解
练一练
3
已知 a2n=3,求 a4n-a6n 的值.
解:a4n-a6n = (a2n)2- (a2n)3
= 32-33
= -18 .
把指数是积的形式的幂写成幂的乘方,amn=(am)n
(m,n都是正整数),然后整体代入,求出式子的值.
课堂小结
幂的乘方
(am)n=amn (m,n为正整数)
性质:幂的乘方,底数不变,指数相乘.
当堂小练
1.计算(x3)3的结果是( )
A. x5 B. x6 C. x8 D. x9
D
2. 下列运算正确的是( )
A. a2·a3=a6 B. (a2)3=a6
C. a5·a5=a25 D. (3x)3=3x3
B
a5
a10
27x3
当堂小练
3. (1)若2x+y=3,则4x·2y= .
(2)已知3m·9m·27m·81m=330,求m的值.
8
解:3m·32m·33m·34m=330
310m=330
m=3
拓展与延伸
已知16m=4×22n-2,27n=9×3m+3 ,求 m,n 的值.
解:因为16m=4×22n-2,所以24m =22×22n-2 .
所以24m=22n,即4m=2n,2m=n. ①
因为 27n=9×3m+3 ,所以(33)n=32×3m+3 .
所以33n=3m+5,即3n=m+5. ②
由①②得,m=1,n=2.
拓展与延伸
比较 355、444 、533 的大小.
解: 355 = (35)11 = 24311 , 444 = (44)11 = 25611 ,
533 = (53)11 = 12511 .
因为125<243<256,则12511<24311<25611 .
所以 533<355< 444 .
布置作业
请完成P68对应习题
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
