5.3 平行线的性质 课时训练(解析版)
文档属性
| 名称 | 5.3 平行线的性质 课时训练(解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 280.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-16 07:40:02 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2021年七年级数学下册课时训练:5.3《平行线的性质》
班级__________姓名__________学号__________
一.选择题(共7小题)
1.下列语句中,为真命题的是( )
A.过一点有且只有一条直线与已知直线平行
B.有理数与数轴上的点一一对应
C.互为邻补角的角的平分线所在的两条直线互相垂直
D.垂直于同一条直线的两条直线平行
2.有下列命题,其中假命题有( )
①对顶角相等:②垂直于同一条直线的两直线平行;③平行于同一条直线的两直线平行;
④内错角相等.
A.①② B.①③ C.②④ D.③④
3.若两条直线被第三条直线所截,有一对同位角相等,则其中一对同旁内角的角平分线( )
A.互相垂直 B.互相平行 C.相交或平行 D.不相等
4.以下判定中,正确的个数有( )
(1)若a∥b,b∥c,则a∥c (2)若a⊥b,b⊥c,则a⊥c
(3)若同旁内角相等,则两直线平行 (4)若同位角相等,则两直线平行.
A.1个 B.2个 C.3个 D.4个
5.如图,直线a,b被直线c所截,a∥b,∠1=50°,则∠2的度数是( )
A.40° B.50° C.60° D.70°
6.如图所示,已知a∥b,将含30°角的三角板如图所示放置,∠1=115°,则∠2的度数为( )
A.25° B.45° C.55° D.65°
7.如图,AB∥CD,EF⊥BD垂足为F,∠1=40°,则∠2的度数为( )
A.30° B.40° C.50° D.60°
二.填空题(共7小题)
8.命题“对顶角相等”的题设是 ,结论是这两个角相等.
9.如图,a∥b,若∠1=50°,则∠2= .
10.如图,已知AB∥CD,∠1=110°,则∠A的度数为 .
11.给出下列命题:
①若a2=b2,则a=b. ②内错角相等,两直线平行. ③若a,b是有理数,则|a+b|=|a|+|b|.
④如果∠A=∠B,那么∠A与∠B是对顶角. ⑤如果a<b,b<c,那么a<c.
其中真命题有 .
12.如图,a∥b,∠2=95°,∠3=150°,则∠1的度数是 .
13.在同一平面内,∠A与∠B的两边分别平行,若∠A=50°,则∠B的度数为 °.
14.如图,∠B=∠C,∠A=∠D,有下列结论:①AB∥CD;②AE∥DF;③AE⊥BC;④∠AMC=∠BND.其中正确的有 .(只填序号)
三.解答题(共6小题)
15.如图所示,AB∥CD,AC∥BD.分别找出与∠1相等或互补的角.
16.请结合图形完成下列推理过程:
(1)∵∠2+∠4=180°,
∴DE∥AC ( ).
(2)∵∠1=∠C,
∴DE∥ ( ).
(3)∵AB∥DF,
∴∠2=∠ ( ).
(4)∵ ∥ ,
∴∠B=∠3 ( ).
17.已知:如图,DB⊥AF于点G,EC⊥AF于点H,∠C=∠D.求证:∠A=∠F.
证明:∵DB⊥AF于点G,EC⊥AF于点H(已知),
∴∠DGH=∠EHF=90°( ).
∴DB∥EC( ).
∴∠C= ( ).
∵∠C=∠D(已知),
∴∠D= ( ).
∴DF∥AC( ).
∴∠A=∠F( ).
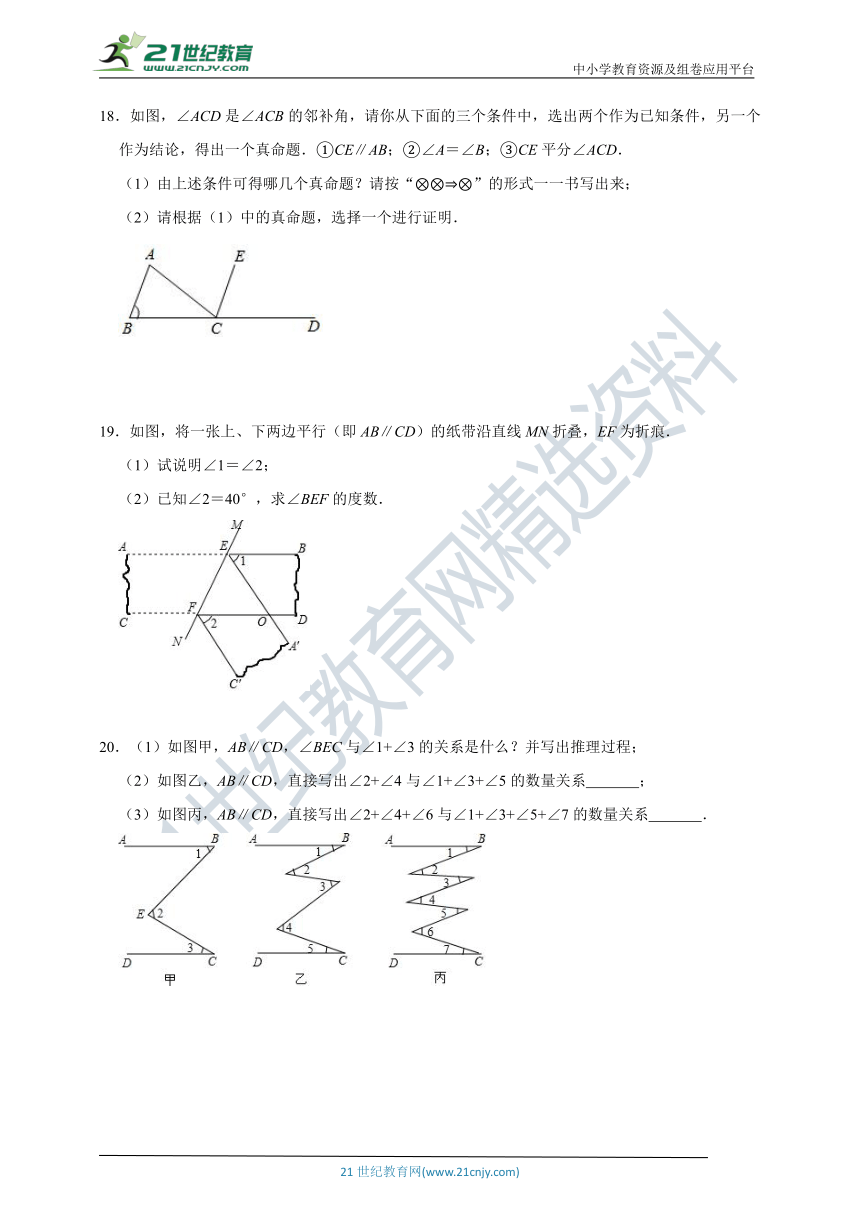
18.如图,∠ACD是∠ACB的邻补角,请你从下面的三个条件中,选出两个作为已知条件,另一个作为结论,得出一个真命题.①CE∥AB;②∠A=∠B;③CE平分∠ACD.
(1)由上述条件可得哪几个真命题?请按“????”的形式一一书写出来;
(2)请根据(1)中的真命题,选择一个进行证明.
19.如图,将一张上、下两边平行(即AB∥CD)的纸带沿直线MN折叠,EF为折痕.
(1)试说明∠1=∠2;
(2)已知∠2=40°,求∠BEF的度数.
20.(1)如图甲,AB∥CD,∠BEC与∠1+∠3的关系是什么?并写出推理过程;
(2)如图乙,AB∥CD,直接写出∠2+∠4与∠1+∠3+∠5的数量关系 ;
(3)如图丙,AB∥CD,直接写出∠2+∠4+∠6与∠1+∠3+∠5+∠7的数量关系 .
参考答案
一.选择题(共7小题)
1.【解答】解:A、过直线外一点有且只有一条直线与已知直线平行,故原命题错误,是假命题,不符合题意;
B、实数与数轴上的点一一对应,故原命题错误,是假命题,不符合题意;
C、互为邻补角的角的平分线所在的两条直线互相垂直,正确,是真命题,符合题意;
D、平面内垂直于同一直线的两条直线平行,故原命题错误,是假命题,不符合题意;
故选:C.
2.【解答】解:①对顶角相等,是真命题,不合题意:
②垂直于同一条直线的两直线平行,缺少在同一平面内,故原命题是假命题,符合题意;
③平行于同一条直线的两直线平行,故原命题是真命题,不符合题意;
④内错角相等,缺少两直线平行,故原命题是假命题,符合题意.
故选:C.
3.【解答】解:如图,
∵∠APE=∠CQE,
∴AB∥CD,
∴∠BPQ+∠DQP=180°,
∵PM平分∠BPQ,QN平分∠DQP,
∴∠BPQ=2∠MPQ,∠DQP=2∠NQP,
∴∠MPQ+∠NQP=90°,
∴∠POQ=90°,
即PM⊥QN,
故选:A.
4.【解答】解:(1)若a∥b,b∥c,则根据平行公理可得a∥c,故正确;
(2)若a⊥b,b⊥c,则a⊥c不一定成立,故错误;
(3)若同旁内角相等,则两直线不一定平行,故错误;
(4)若同位角相等,则两直线平行,故正确.
故选:B.
5.【解答】解:∵a∥b,
∴∠1=∠2,
∵∠1=50°,
∴∠2=50°,
故选:B.
6.【解答】解:∵直线a∥b,
∴∠3=∠1=115°.
又∵∠3=∠2+∠4,
∴∠2=∠3﹣∠4=115°﹣60°=55°.
故选:C.
7.【解答】解:∵AB∥CD,
∴∠D=∠1=40°.
∵EF⊥BD,
∴∠DFE=90°,
∴∠2=180°﹣∠DFE﹣∠D=50°.
故选:C.
二.填空题(共7小题)
8.【解答】解:命题“对顶角相等”可写成:如果两个角是对顶角,那么这两个角相等.
故命题“对顶角相等”的题设是“两个角是对顶角”.
故答案为:两个角是对顶角.
9.【解答】解:
∵a∥b,∠1=50°,
∴∠1=∠3=50°,
∴∠2=180°﹣∠3=130°,
故答案为:130°.
10.【解答】解:如图,∠1=∠2=110°,
∵AB∥CD,
∴∠A+∠2=180°,
∴∠A=180°﹣∠2=70°,
故答案为:70°.
11.【解答】解:①若a2=b2,则a=±b,故原命题错误,是假命题,不符合题意.
②内错角相等,两直线平行,正确,是真命题,符合题意.
③若a,b是有理数,则|a+b|=|a|+|b|,错误,是假命题,不符合题意.
④如果∠A=∠B,那么∠A与∠B是对顶角长,错误,是假命题,不符合题意.
⑤如果a<b,b<c,那么a<c,正确,是真命题,符合题意.
真命题有②⑤,
故答案为:②⑤.
12.【解答】解:过点C作CD∥a,
∵a∥b,
∴CD∥a∥b,
∴∠1+∠ECD=180°,∠3+∠DCF=180°,
∵∠2=95°,∠3=150°,
∴∠1+∠2+∠3=360°,
∴∠1=360°﹣∠2﹣∠3=360°﹣150°﹣95°=115°,
故答案为:115°.
13.【解答】解:∵∠A与∠B的两边分别平行,
∴∠A=∠B或∠A+∠B=180°,
∵∠A=50°,
∴∠B=50°,或∠B=180°﹣∠A=180°﹣50°=130°.
故答案为:50或130.
14.【解答】解:∵∠B=∠C,
∴AB∥CD,
∴∠A=∠AEC,
又∵∠A=∠D,
∴∠AEC=∠D,
∴AE∥DF,
∴∠AMC=∠FNM,
又∵∠BND=∠FNM,
∴∠AMC=∠BND,
故①②④正确,
由条件不能得出∠AMC=90°,故③不一定正确;
故答案为:①②④.
三.解答题(共6小题)
15.【解答】解:∵AB∥CD,AC∥BD,
∴∠GCQ=∠1=∠PAB=∠EAC,∠1+∠CAF=∠1+∠ACG=∠1+∠QCH=180°,
∠CDN=∠1=∠BDH=∠MBF=∠ABD,∠1+∠CDB=∠1+∠NDH=∠1+∠DBF=∠1+∠ABM=180°,
即与∠1相等的角为∠GCQ、∠PAB、∠EAC、∠CDN、∠BDH、∠MBF、∠ABD,
与∠1互补的角为∠CAF、∠ACG、∠QCH、∠CDB、∠NDH、∠DBF、∠ABM.
16.【解答】解:(1)∵∠2+∠4=180°,
∴DE∥AC (同旁内角互补,两直线平行 ).
(2)∵∠1=∠C,
∴DE∥AC(同位角相等,两直线平行).
(3)∵AB∥DF,
∴∠2=∠BED(两直线平行,内错角相等).
(4)∵AB∥DF,
∴∠B=∠3 (两直线平行,同位角相等).
故答案为:同旁内角互补,两直线平行;AC,同位角相等,两直线平行;
BED,两直线平行,内错角相等;AB,DF,两直线平行,同位角相等.
17.【解答】解:∵DB⊥AF于点G,EC⊥AF于点H(已知),
∴∠DGH=∠EHF=90°(垂直的定义),
∴DB∥EC(同位角相等,两直线平行),
∴∠C=∠DBA(两直线平行,同位角相等),
∵∠C=∠D(已知),
∴∠D=∠DBA(等量代换),
∴DF∥AC(内错角相等,两直线平行),
∴∠A=∠F(两直线平行,内错角相等).
故答案为:垂直的定义;同位角相等,两直线平行;∠DBA,两直线平行,同位角相等;∠DBA,等量代换;内错角相等,两直线平行;两直线平行,内错角相等.
18.【解答】解:(1)上述问题有三种正确命题,分别是:
命题1:①②?③;命题2:①③?②;命题3:②③?①.
(2)解:选择命题2:①③?②.
证明:∵CE∥AB,∴∠ACE=∠A,∠DCE=∠B.
∵CE平分∠ACD,∴∠ACE=∠DCE.
∴∠A=∠B.
19.【解答】解:(1)∵AB∥CD,∴∠MEB=∠MFD,
∵A′E∥C′F,
∴∠MEA′=∠MFC′,
∴∠MEA′﹣∠MEB=∠MFC′﹣∠MFD,
即∠1=∠2;
(2)由折叠知,∠C′FN==70°,
∵A′E∥C′F,
∴∠A′EN=∠C′FN=70°,
∵∠1=∠2,
∴∠BEF=70°+40°=110°.
20.【解答】解:(1)∠BEC=∠1+∠3.
证明:过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠BEF=∠1,∠CEF=∠3,
∴∠BEC=∠BEF+∠CEF=∠1+∠3;
(2)∠2+∠4=∠1+∠3+∠5.
理由:分别过点E,G,M,作EF∥AB,GH∥AB,MN∥AB,
∵AB∥CD,
∴AB∥CD∥EF∥GH∥MN,
∴∠1=∠BEF,∠FEG=∠EGH,∠HGM=∠GMN,∠CMN=∠5,
∴∠2+∠4=∠BEF+∠FEG+∠GMN+∠CMN=∠1+∠EGH+∠MGH+∠5=∠1+∠3+∠5;
(3)∠2+∠4+∠6=∠1+∠3+∠5+∠7.
理由:分别过点E,G,M,K,P,作EF∥AB,GH∥AB,MN∥AB,KL∥AB,PQ∥AB,
∵AB∥CD,
∴AB∥CD∥EF∥GH∥MN∥KL∥PQ,
∴∠1=∠BEF,∠FEG=∠EGH,∠HGM=∠GMN,∠KMN=∠LKM,∠LKP=∠KPQ,∠QPC=∠7,
∴∠2+∠4+∠6=∠1+∠3+∠5+∠7.
_21?????????è?????(www.21cnjy.com)_
2021年七年级数学下册课时训练:5.3《平行线的性质》
班级__________姓名__________学号__________
一.选择题(共7小题)
1.下列语句中,为真命题的是( )
A.过一点有且只有一条直线与已知直线平行
B.有理数与数轴上的点一一对应
C.互为邻补角的角的平分线所在的两条直线互相垂直
D.垂直于同一条直线的两条直线平行
2.有下列命题,其中假命题有( )
①对顶角相等:②垂直于同一条直线的两直线平行;③平行于同一条直线的两直线平行;
④内错角相等.
A.①② B.①③ C.②④ D.③④
3.若两条直线被第三条直线所截,有一对同位角相等,则其中一对同旁内角的角平分线( )
A.互相垂直 B.互相平行 C.相交或平行 D.不相等
4.以下判定中,正确的个数有( )
(1)若a∥b,b∥c,则a∥c (2)若a⊥b,b⊥c,则a⊥c
(3)若同旁内角相等,则两直线平行 (4)若同位角相等,则两直线平行.
A.1个 B.2个 C.3个 D.4个
5.如图,直线a,b被直线c所截,a∥b,∠1=50°,则∠2的度数是( )
A.40° B.50° C.60° D.70°
6.如图所示,已知a∥b,将含30°角的三角板如图所示放置,∠1=115°,则∠2的度数为( )
A.25° B.45° C.55° D.65°
7.如图,AB∥CD,EF⊥BD垂足为F,∠1=40°,则∠2的度数为( )
A.30° B.40° C.50° D.60°
二.填空题(共7小题)
8.命题“对顶角相等”的题设是 ,结论是这两个角相等.
9.如图,a∥b,若∠1=50°,则∠2= .
10.如图,已知AB∥CD,∠1=110°,则∠A的度数为 .
11.给出下列命题:
①若a2=b2,则a=b. ②内错角相等,两直线平行. ③若a,b是有理数,则|a+b|=|a|+|b|.
④如果∠A=∠B,那么∠A与∠B是对顶角. ⑤如果a<b,b<c,那么a<c.
其中真命题有 .
12.如图,a∥b,∠2=95°,∠3=150°,则∠1的度数是 .
13.在同一平面内,∠A与∠B的两边分别平行,若∠A=50°,则∠B的度数为 °.
14.如图,∠B=∠C,∠A=∠D,有下列结论:①AB∥CD;②AE∥DF;③AE⊥BC;④∠AMC=∠BND.其中正确的有 .(只填序号)
三.解答题(共6小题)
15.如图所示,AB∥CD,AC∥BD.分别找出与∠1相等或互补的角.
16.请结合图形完成下列推理过程:
(1)∵∠2+∠4=180°,
∴DE∥AC ( ).
(2)∵∠1=∠C,
∴DE∥ ( ).
(3)∵AB∥DF,
∴∠2=∠ ( ).
(4)∵ ∥ ,
∴∠B=∠3 ( ).
17.已知:如图,DB⊥AF于点G,EC⊥AF于点H,∠C=∠D.求证:∠A=∠F.
证明:∵DB⊥AF于点G,EC⊥AF于点H(已知),
∴∠DGH=∠EHF=90°( ).
∴DB∥EC( ).
∴∠C= ( ).
∵∠C=∠D(已知),
∴∠D= ( ).
∴DF∥AC( ).
∴∠A=∠F( ).
18.如图,∠ACD是∠ACB的邻补角,请你从下面的三个条件中,选出两个作为已知条件,另一个作为结论,得出一个真命题.①CE∥AB;②∠A=∠B;③CE平分∠ACD.
(1)由上述条件可得哪几个真命题?请按“????”的形式一一书写出来;
(2)请根据(1)中的真命题,选择一个进行证明.
19.如图,将一张上、下两边平行(即AB∥CD)的纸带沿直线MN折叠,EF为折痕.
(1)试说明∠1=∠2;
(2)已知∠2=40°,求∠BEF的度数.
20.(1)如图甲,AB∥CD,∠BEC与∠1+∠3的关系是什么?并写出推理过程;
(2)如图乙,AB∥CD,直接写出∠2+∠4与∠1+∠3+∠5的数量关系 ;
(3)如图丙,AB∥CD,直接写出∠2+∠4+∠6与∠1+∠3+∠5+∠7的数量关系 .
参考答案
一.选择题(共7小题)
1.【解答】解:A、过直线外一点有且只有一条直线与已知直线平行,故原命题错误,是假命题,不符合题意;
B、实数与数轴上的点一一对应,故原命题错误,是假命题,不符合题意;
C、互为邻补角的角的平分线所在的两条直线互相垂直,正确,是真命题,符合题意;
D、平面内垂直于同一直线的两条直线平行,故原命题错误,是假命题,不符合题意;
故选:C.
2.【解答】解:①对顶角相等,是真命题,不合题意:
②垂直于同一条直线的两直线平行,缺少在同一平面内,故原命题是假命题,符合题意;
③平行于同一条直线的两直线平行,故原命题是真命题,不符合题意;
④内错角相等,缺少两直线平行,故原命题是假命题,符合题意.
故选:C.
3.【解答】解:如图,
∵∠APE=∠CQE,
∴AB∥CD,
∴∠BPQ+∠DQP=180°,
∵PM平分∠BPQ,QN平分∠DQP,
∴∠BPQ=2∠MPQ,∠DQP=2∠NQP,
∴∠MPQ+∠NQP=90°,
∴∠POQ=90°,
即PM⊥QN,
故选:A.
4.【解答】解:(1)若a∥b,b∥c,则根据平行公理可得a∥c,故正确;
(2)若a⊥b,b⊥c,则a⊥c不一定成立,故错误;
(3)若同旁内角相等,则两直线不一定平行,故错误;
(4)若同位角相等,则两直线平行,故正确.
故选:B.
5.【解答】解:∵a∥b,
∴∠1=∠2,
∵∠1=50°,
∴∠2=50°,
故选:B.
6.【解答】解:∵直线a∥b,
∴∠3=∠1=115°.
又∵∠3=∠2+∠4,
∴∠2=∠3﹣∠4=115°﹣60°=55°.
故选:C.
7.【解答】解:∵AB∥CD,
∴∠D=∠1=40°.
∵EF⊥BD,
∴∠DFE=90°,
∴∠2=180°﹣∠DFE﹣∠D=50°.
故选:C.
二.填空题(共7小题)
8.【解答】解:命题“对顶角相等”可写成:如果两个角是对顶角,那么这两个角相等.
故命题“对顶角相等”的题设是“两个角是对顶角”.
故答案为:两个角是对顶角.
9.【解答】解:
∵a∥b,∠1=50°,
∴∠1=∠3=50°,
∴∠2=180°﹣∠3=130°,
故答案为:130°.
10.【解答】解:如图,∠1=∠2=110°,
∵AB∥CD,
∴∠A+∠2=180°,
∴∠A=180°﹣∠2=70°,
故答案为:70°.
11.【解答】解:①若a2=b2,则a=±b,故原命题错误,是假命题,不符合题意.
②内错角相等,两直线平行,正确,是真命题,符合题意.
③若a,b是有理数,则|a+b|=|a|+|b|,错误,是假命题,不符合题意.
④如果∠A=∠B,那么∠A与∠B是对顶角长,错误,是假命题,不符合题意.
⑤如果a<b,b<c,那么a<c,正确,是真命题,符合题意.
真命题有②⑤,
故答案为:②⑤.
12.【解答】解:过点C作CD∥a,
∵a∥b,
∴CD∥a∥b,
∴∠1+∠ECD=180°,∠3+∠DCF=180°,
∵∠2=95°,∠3=150°,
∴∠1+∠2+∠3=360°,
∴∠1=360°﹣∠2﹣∠3=360°﹣150°﹣95°=115°,
故答案为:115°.
13.【解答】解:∵∠A与∠B的两边分别平行,
∴∠A=∠B或∠A+∠B=180°,
∵∠A=50°,
∴∠B=50°,或∠B=180°﹣∠A=180°﹣50°=130°.
故答案为:50或130.
14.【解答】解:∵∠B=∠C,
∴AB∥CD,
∴∠A=∠AEC,
又∵∠A=∠D,
∴∠AEC=∠D,
∴AE∥DF,
∴∠AMC=∠FNM,
又∵∠BND=∠FNM,
∴∠AMC=∠BND,
故①②④正确,
由条件不能得出∠AMC=90°,故③不一定正确;
故答案为:①②④.
三.解答题(共6小题)
15.【解答】解:∵AB∥CD,AC∥BD,
∴∠GCQ=∠1=∠PAB=∠EAC,∠1+∠CAF=∠1+∠ACG=∠1+∠QCH=180°,
∠CDN=∠1=∠BDH=∠MBF=∠ABD,∠1+∠CDB=∠1+∠NDH=∠1+∠DBF=∠1+∠ABM=180°,
即与∠1相等的角为∠GCQ、∠PAB、∠EAC、∠CDN、∠BDH、∠MBF、∠ABD,
与∠1互补的角为∠CAF、∠ACG、∠QCH、∠CDB、∠NDH、∠DBF、∠ABM.
16.【解答】解:(1)∵∠2+∠4=180°,
∴DE∥AC (同旁内角互补,两直线平行 ).
(2)∵∠1=∠C,
∴DE∥AC(同位角相等,两直线平行).
(3)∵AB∥DF,
∴∠2=∠BED(两直线平行,内错角相等).
(4)∵AB∥DF,
∴∠B=∠3 (两直线平行,同位角相等).
故答案为:同旁内角互补,两直线平行;AC,同位角相等,两直线平行;
BED,两直线平行,内错角相等;AB,DF,两直线平行,同位角相等.
17.【解答】解:∵DB⊥AF于点G,EC⊥AF于点H(已知),
∴∠DGH=∠EHF=90°(垂直的定义),
∴DB∥EC(同位角相等,两直线平行),
∴∠C=∠DBA(两直线平行,同位角相等),
∵∠C=∠D(已知),
∴∠D=∠DBA(等量代换),
∴DF∥AC(内错角相等,两直线平行),
∴∠A=∠F(两直线平行,内错角相等).
故答案为:垂直的定义;同位角相等,两直线平行;∠DBA,两直线平行,同位角相等;∠DBA,等量代换;内错角相等,两直线平行;两直线平行,内错角相等.
18.【解答】解:(1)上述问题有三种正确命题,分别是:
命题1:①②?③;命题2:①③?②;命题3:②③?①.
(2)解:选择命题2:①③?②.
证明:∵CE∥AB,∴∠ACE=∠A,∠DCE=∠B.
∵CE平分∠ACD,∴∠ACE=∠DCE.
∴∠A=∠B.
19.【解答】解:(1)∵AB∥CD,∴∠MEB=∠MFD,
∵A′E∥C′F,
∴∠MEA′=∠MFC′,
∴∠MEA′﹣∠MEB=∠MFC′﹣∠MFD,
即∠1=∠2;
(2)由折叠知,∠C′FN==70°,
∵A′E∥C′F,
∴∠A′EN=∠C′FN=70°,
∵∠1=∠2,
∴∠BEF=70°+40°=110°.
20.【解答】解:(1)∠BEC=∠1+∠3.
证明:过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠BEF=∠1,∠CEF=∠3,
∴∠BEC=∠BEF+∠CEF=∠1+∠3;
(2)∠2+∠4=∠1+∠3+∠5.
理由:分别过点E,G,M,作EF∥AB,GH∥AB,MN∥AB,
∵AB∥CD,
∴AB∥CD∥EF∥GH∥MN,
∴∠1=∠BEF,∠FEG=∠EGH,∠HGM=∠GMN,∠CMN=∠5,
∴∠2+∠4=∠BEF+∠FEG+∠GMN+∠CMN=∠1+∠EGH+∠MGH+∠5=∠1+∠3+∠5;
(3)∠2+∠4+∠6=∠1+∠3+∠5+∠7.
理由:分别过点E,G,M,K,P,作EF∥AB,GH∥AB,MN∥AB,KL∥AB,PQ∥AB,
∵AB∥CD,
∴AB∥CD∥EF∥GH∥MN∥KL∥PQ,
∴∠1=∠BEF,∠FEG=∠EGH,∠HGM=∠GMN,∠KMN=∠LKM,∠LKP=∠KPQ,∠QPC=∠7,
∴∠2+∠4+∠6=∠1+∠3+∠5+∠7.
_21?????????è?????(www.21cnjy.com)_
