北师大版 八年级数学下册 1.2 直角三角形 同步练习 (Word版 含答案)
文档属性
| 名称 | 北师大版 八年级数学下册 1.2 直角三角形 同步练习 (Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 84.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-16 05:47:28 | ||
图片预览

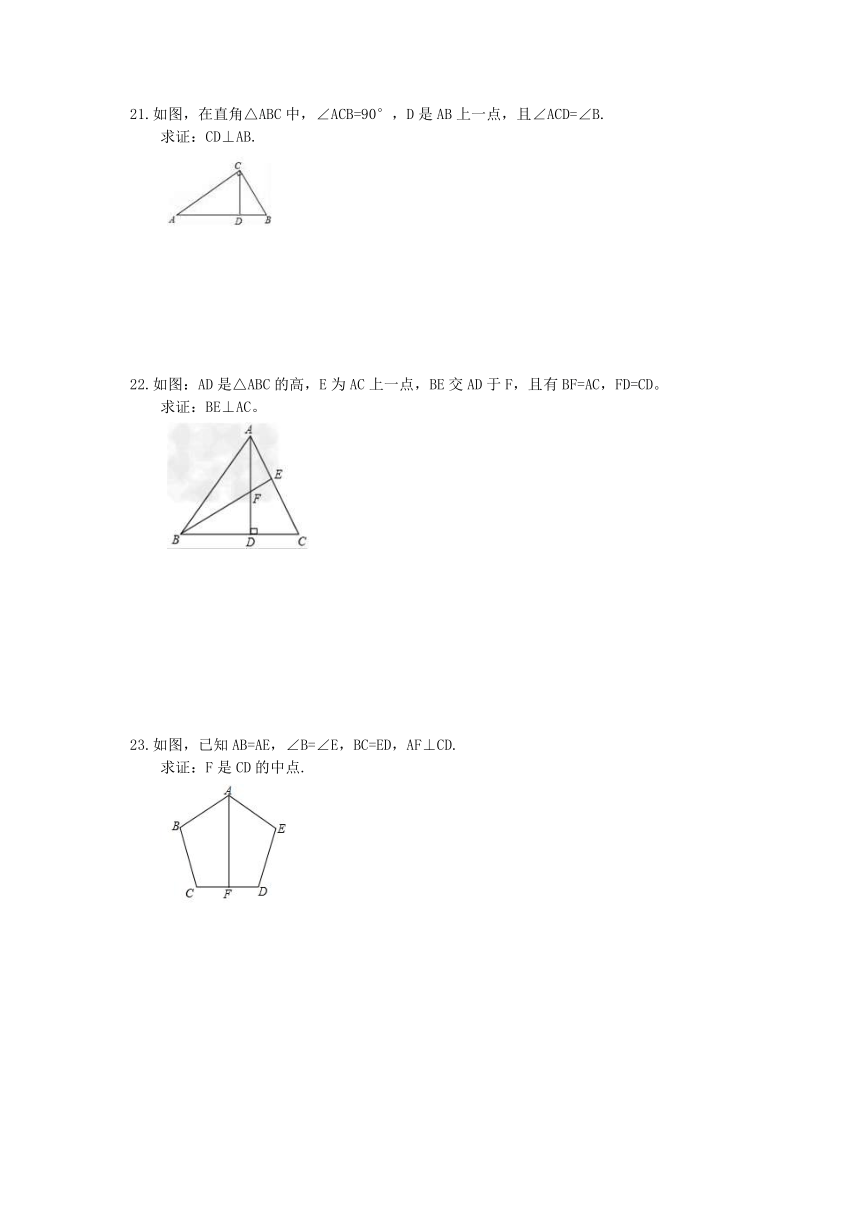
文档简介
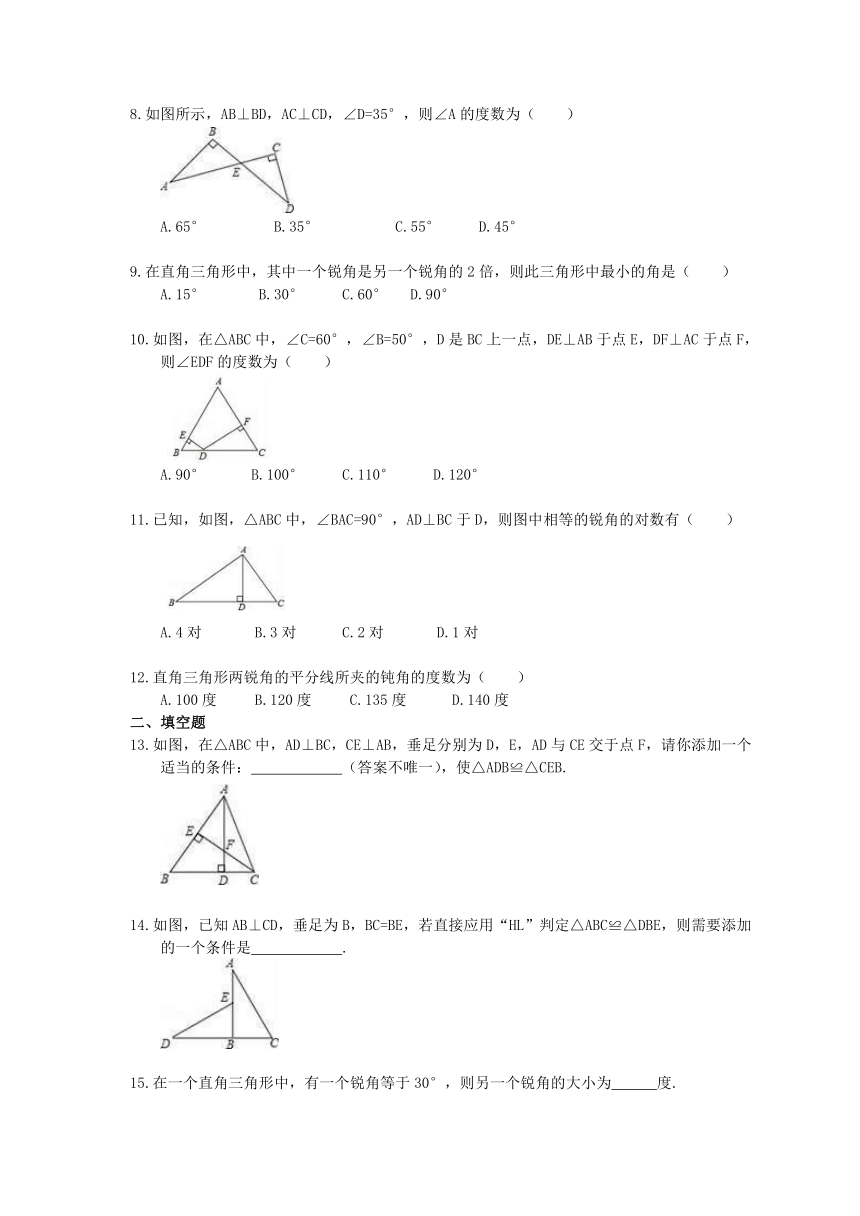
北师大版数学八年级下册1.2《直角三角形》
精选练习
一、选择题
1.如图,若要用“HL”证明Rt△ABC≌Rt△ABD,则还需补充条件( )
A.∠BAC=∠BAD B.AC=AD或BC=BD C.AC=AD且BC=BD D.以上都不正确
2.下列可使两个直角三角形全等的条件是( )
A.一条边对应相等
B.两条直角边对应相等
C.一个锐角对应相等
D.两个锐角对应相等
3.如图,O是∠BAC内一点,且点O到AB,AC的距离OE=OF,则△AEO≌△AFO的依据是( )
A.HL B.AAS C.SSS D.ASA
4.如果两个直角三角形的两条直角边对应相等,那么这两个直角三角形全等的依据是( )
A.SSS B.AAS C.SAS D.HL
5.将一副直角三角尺如图放置,若∠AOD=20°,则∠BOC的大小为( )
A.140° B.160° C.170° D.150°
6.Rt△ABC中,∠C=90°,∠B=46°,则∠A=( )
A.44° B.34° C.54° D.64°
7.如图,一个矩形纸片,剪去部分后得到一个三角形,则图中∠1+∠2的度数是( )
A.30° B.60° C.90° D.120°
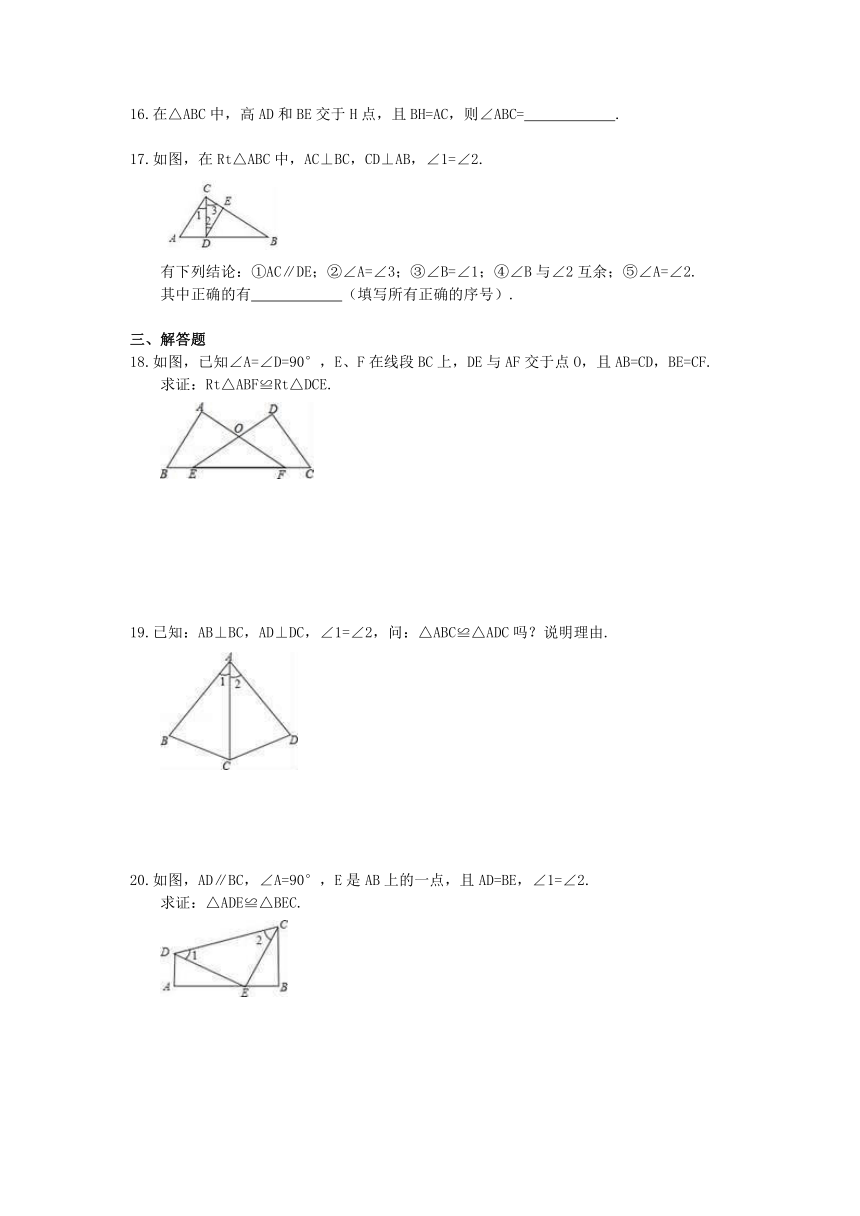
8.如图所示,AB⊥BD,AC⊥CD,∠D=35°,则∠A的度数为( )
A.65° B.35° C.55° D.45°
9.在直角三角形中,其中一个锐角是另一个锐角的2倍,则此三角形中最小的角是( )
A.15° B.30° C.60° D.90°
10.如图,在△ABC中,∠C=60°,∠B=50°,D是BC上一点,DE⊥AB于点E,DF⊥AC于点F,则∠EDF的度数为( )
A.90° B.100° C.110° D.120°
11.已知,如图,△ABC中,∠BAC=90°,AD⊥BC于D,则图中相等的锐角的对数有( )
A.4对 B.3对 C.2对 D.1对
12.直角三角形两锐角的平分线所夹的钝角的度数为( )
A.100度 B.120度 C.135度 D.140度
二、填空题
13.如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD与CE交于点F,请你添加一个适当的条件: (答案不唯一),使△ADB≌△CEB.
14.如图,已知AB⊥CD,垂足为B,BC=BE,若直接应用“HL”判定△ABC≌△DBE,则需要添加的一个条件是 .
15.在一个直角三角形中,有一个锐角等于30°,则另一个锐角的大小为 度.
16.在△ABC中,高AD和BE交于H点,且BH=AC,则∠ABC= .
17.如图,在Rt△ABC中,AC⊥BC,CD⊥AB,∠1=∠2.
有下列结论:①AC∥DE;②∠A=∠3;③∠B=∠1;④∠B与∠2互余;⑤∠A=∠2.
其中正确的有 (填写所有正确的序号).
三、解答题
18.如图,已知∠A=∠D=90°,E、F在线段BC上,DE与AF交于点O,且AB=CD,BE=CF.
求证:Rt△ABF≌Rt△DCE.
19.已知:AB⊥BC,AD⊥DC,∠1=∠2,问:△ABC≌△ADC吗?说明理由.
20.如图,AD∥BC,∠A=90°,E是AB上的一点,且AD=BE,∠1=∠2.
求证:△ADE≌△BEC.
21.如图,在直角△ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B.
求证:CD⊥AB.
22.如图:AD是△ABC的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD。
求证:BE⊥AC。
23.如图,已知AB=AE,∠B=∠E,BC=ED,AF⊥CD.
求证:F是CD的中点.
24.在△ABC中,OE⊥AB,OF⊥AC且OE=OF.
(1)如图,当点O在BC边中点时,试说明AB=AC;
(2)如图,当点O在△ABC内部时,且OB=OC,试说明AB与AC的关系;
(3)当点O在△ABC外部时,且OB=OC,试判断AB与AC的关系.(画出图形,写出结果即可,无须说明理由)
参考答案
答案为:B
答案为:B
答案为:A
答案为:C
答案为:B
答案为:A
答案为:C
答案为:B
答案为:B
答案为:C
答案为:C
答案为:C
答案为:AB=BC
答案为:AC=DE
答案为:60
答案为:45°或135°
答案为:①②③
证明:∵BE=CF,
∴BE+EF=CF+EF,即BF=CE,
∵∠A=∠D=90°,
∴△ABF与△DCE都为直角三角形,
在Rt△ABF和Rt△DCE中,
∴Rt△ABF≌Rt△DCE(HL).
解:△ABC≌△ADC.理由如下:
∵AB⊥BC,AD⊥DC,
∴∠B=∠D=90°.
在△ABC与△ADC中,
∴△ABC≌△ADC(AAS).
证明:∵∠1=∠2,
∴DE=CE.
∵AD∥BC,∠A=90°,
∴∠B=90°.
∴△ADE和△EBC是直角三角形,而AD=BE.
∴△ADE≌△BEC.
证明:∵∠ACB=90°,
∴∠A+∠B=90°,
∵∠ACD=∠B,
∴∠A+∠ACD=90°,
∴∠ADC=90°,
∴CD⊥AB.
证明:(1) AD为△ABC上的高,
∴BDA=ADC =90.
∵BF=AC,FD=CD.
∴Rt△BDF≌Rt△ADC.
(2)由①知∠C=∠BFD,∠CAD=∠DBF.
∠BFD= ∠AFE,又∠CBE=∠CAD,
∴∠AEF=∠BDF.
∠BDF= 90,
∴BE⊥AC.
证明:连接AC,AD.
在△ABC和△AED中,
∴△ABC≌△AED(SAS).
∴AC=AD.
在Rt△ACF和Rt△ADF中,
∴Rt△ACF≌Rt△ADF(HL).
∴CF=DF,
即F为CD的中点.
(1)证明:∵OE=OF,OB=OC,
∴Rt△OBE≌Rt△OCF(HL);
∴∠B=∠C,
∴AB=AC.
(2)AB=AC.
证明:同(1)可证得Rt△OBE≌Rt△OCF;
∴∠OBE=∠OCF;
∵OB=OC,
∴∠OBC=∠OCB;
∴∠ABC=∠ACB;
∴AB=AC.
(3)解:当BC的垂直平分线与∠A的平分线重合时,AB=AC成立,如图①;
当BC的垂直平分线与∠A的平分线不在一条直线上时,结论不成立,如图②.
精选练习
一、选择题
1.如图,若要用“HL”证明Rt△ABC≌Rt△ABD,则还需补充条件( )
A.∠BAC=∠BAD B.AC=AD或BC=BD C.AC=AD且BC=BD D.以上都不正确
2.下列可使两个直角三角形全等的条件是( )
A.一条边对应相等
B.两条直角边对应相等
C.一个锐角对应相等
D.两个锐角对应相等
3.如图,O是∠BAC内一点,且点O到AB,AC的距离OE=OF,则△AEO≌△AFO的依据是( )
A.HL B.AAS C.SSS D.ASA
4.如果两个直角三角形的两条直角边对应相等,那么这两个直角三角形全等的依据是( )
A.SSS B.AAS C.SAS D.HL
5.将一副直角三角尺如图放置,若∠AOD=20°,则∠BOC的大小为( )
A.140° B.160° C.170° D.150°
6.Rt△ABC中,∠C=90°,∠B=46°,则∠A=( )
A.44° B.34° C.54° D.64°
7.如图,一个矩形纸片,剪去部分后得到一个三角形,则图中∠1+∠2的度数是( )
A.30° B.60° C.90° D.120°
8.如图所示,AB⊥BD,AC⊥CD,∠D=35°,则∠A的度数为( )
A.65° B.35° C.55° D.45°
9.在直角三角形中,其中一个锐角是另一个锐角的2倍,则此三角形中最小的角是( )
A.15° B.30° C.60° D.90°
10.如图,在△ABC中,∠C=60°,∠B=50°,D是BC上一点,DE⊥AB于点E,DF⊥AC于点F,则∠EDF的度数为( )
A.90° B.100° C.110° D.120°
11.已知,如图,△ABC中,∠BAC=90°,AD⊥BC于D,则图中相等的锐角的对数有( )
A.4对 B.3对 C.2对 D.1对
12.直角三角形两锐角的平分线所夹的钝角的度数为( )
A.100度 B.120度 C.135度 D.140度
二、填空题
13.如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD与CE交于点F,请你添加一个适当的条件: (答案不唯一),使△ADB≌△CEB.
14.如图,已知AB⊥CD,垂足为B,BC=BE,若直接应用“HL”判定△ABC≌△DBE,则需要添加的一个条件是 .
15.在一个直角三角形中,有一个锐角等于30°,则另一个锐角的大小为 度.
16.在△ABC中,高AD和BE交于H点,且BH=AC,则∠ABC= .
17.如图,在Rt△ABC中,AC⊥BC,CD⊥AB,∠1=∠2.
有下列结论:①AC∥DE;②∠A=∠3;③∠B=∠1;④∠B与∠2互余;⑤∠A=∠2.
其中正确的有 (填写所有正确的序号).
三、解答题
18.如图,已知∠A=∠D=90°,E、F在线段BC上,DE与AF交于点O,且AB=CD,BE=CF.
求证:Rt△ABF≌Rt△DCE.
19.已知:AB⊥BC,AD⊥DC,∠1=∠2,问:△ABC≌△ADC吗?说明理由.
20.如图,AD∥BC,∠A=90°,E是AB上的一点,且AD=BE,∠1=∠2.
求证:△ADE≌△BEC.
21.如图,在直角△ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B.
求证:CD⊥AB.
22.如图:AD是△ABC的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD。
求证:BE⊥AC。
23.如图,已知AB=AE,∠B=∠E,BC=ED,AF⊥CD.
求证:F是CD的中点.
24.在△ABC中,OE⊥AB,OF⊥AC且OE=OF.
(1)如图,当点O在BC边中点时,试说明AB=AC;
(2)如图,当点O在△ABC内部时,且OB=OC,试说明AB与AC的关系;
(3)当点O在△ABC外部时,且OB=OC,试判断AB与AC的关系.(画出图形,写出结果即可,无须说明理由)
参考答案
答案为:B
答案为:B
答案为:A
答案为:C
答案为:B
答案为:A
答案为:C
答案为:B
答案为:B
答案为:C
答案为:C
答案为:C
答案为:AB=BC
答案为:AC=DE
答案为:60
答案为:45°或135°
答案为:①②③
证明:∵BE=CF,
∴BE+EF=CF+EF,即BF=CE,
∵∠A=∠D=90°,
∴△ABF与△DCE都为直角三角形,
在Rt△ABF和Rt△DCE中,
∴Rt△ABF≌Rt△DCE(HL).
解:△ABC≌△ADC.理由如下:
∵AB⊥BC,AD⊥DC,
∴∠B=∠D=90°.
在△ABC与△ADC中,
∴△ABC≌△ADC(AAS).
证明:∵∠1=∠2,
∴DE=CE.
∵AD∥BC,∠A=90°,
∴∠B=90°.
∴△ADE和△EBC是直角三角形,而AD=BE.
∴△ADE≌△BEC.
证明:∵∠ACB=90°,
∴∠A+∠B=90°,
∵∠ACD=∠B,
∴∠A+∠ACD=90°,
∴∠ADC=90°,
∴CD⊥AB.
证明:(1) AD为△ABC上的高,
∴BDA=ADC =90.
∵BF=AC,FD=CD.
∴Rt△BDF≌Rt△ADC.
(2)由①知∠C=∠BFD,∠CAD=∠DBF.
∠BFD= ∠AFE,又∠CBE=∠CAD,
∴∠AEF=∠BDF.
∠BDF= 90,
∴BE⊥AC.
证明:连接AC,AD.
在△ABC和△AED中,
∴△ABC≌△AED(SAS).
∴AC=AD.
在Rt△ACF和Rt△ADF中,
∴Rt△ACF≌Rt△ADF(HL).
∴CF=DF,
即F为CD的中点.
(1)证明:∵OE=OF,OB=OC,
∴Rt△OBE≌Rt△OCF(HL);
∴∠B=∠C,
∴AB=AC.
(2)AB=AC.
证明:同(1)可证得Rt△OBE≌Rt△OCF;
∴∠OBE=∠OCF;
∵OB=OC,
∴∠OBC=∠OCB;
∴∠ABC=∠ACB;
∴AB=AC.
(3)解:当BC的垂直平分线与∠A的平分线重合时,AB=AC成立,如图①;
当BC的垂直平分线与∠A的平分线不在一条直线上时,结论不成立,如图②.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
