2021春北师大版七下数学1.4整式的乘法教学课件(共19张PPT)
文档属性
| 名称 | 2021春北师大版七下数学1.4整式的乘法教学课件(共19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 564.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-16 10:19:32 | ||
图片预览



文档简介
1.4 整式的乘法
目标导引
掌握正整数幂的运算性质,并能应用性质 熟练地进行运算.
2. 掌握整式乘法的运算法则,并会运用法则
进行简单的整式乘法运算.
能灵活运用平方差公式与完全平方公式进 行计算.
4. 能运用整式的乘法解决一些数学问题和实
际问题.体验整式乘法在数学变形中的重
要作用.
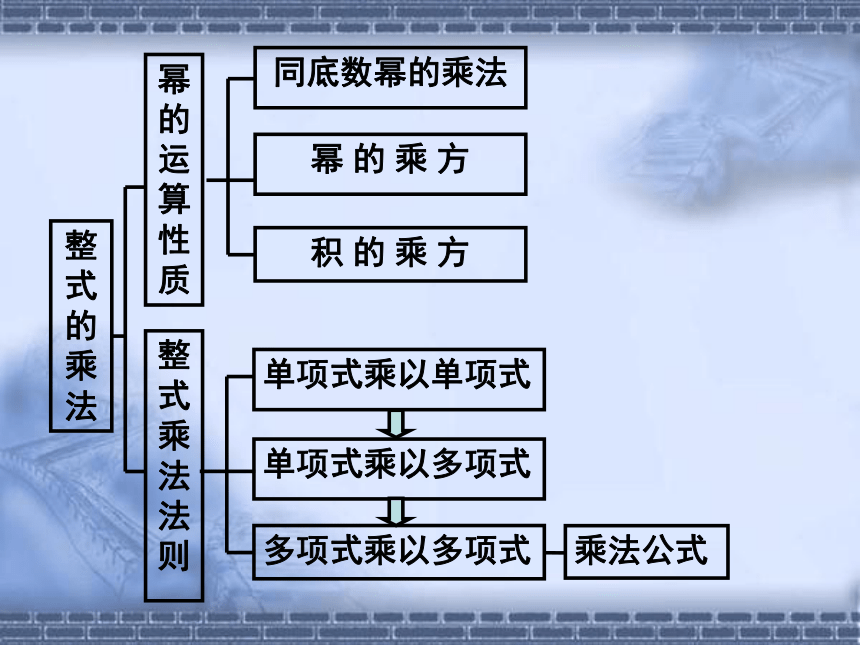
幂的运算性质
同底数幂的乘法
幂 的 乘 方
积 的 乘 方
乘法公式
整式的乘法
整式乘法法则
单项式乘以单项式
单项式乘以多项式
多项式乘以多项式
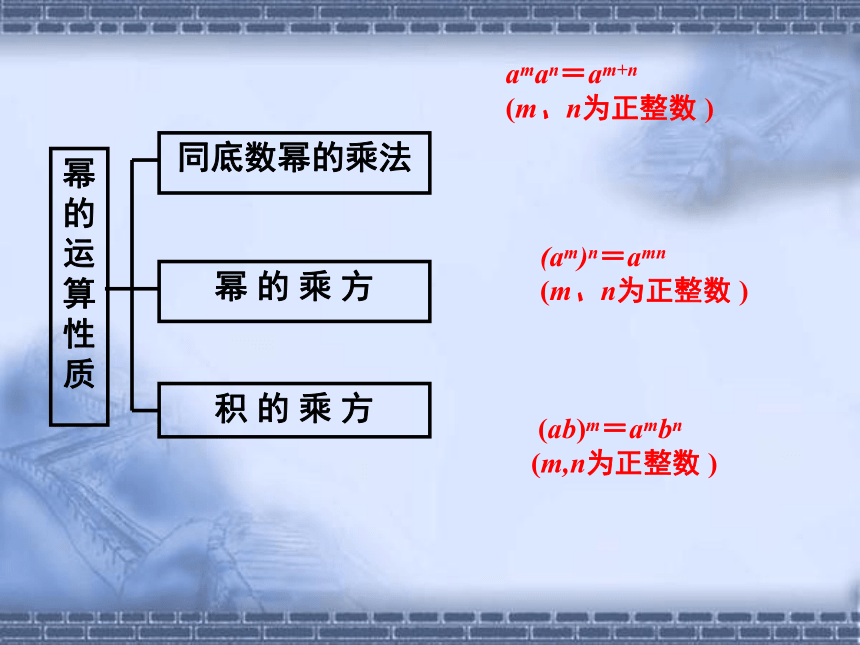
幂的运算性质
同底数幂的乘法
幂 的 乘 方
积 的 乘 方
aman=am+n
(m、n为正整数 )
(am)n=amn
(m、n为正整数 )
(ab)m=ambn
(m,n为正整数 )
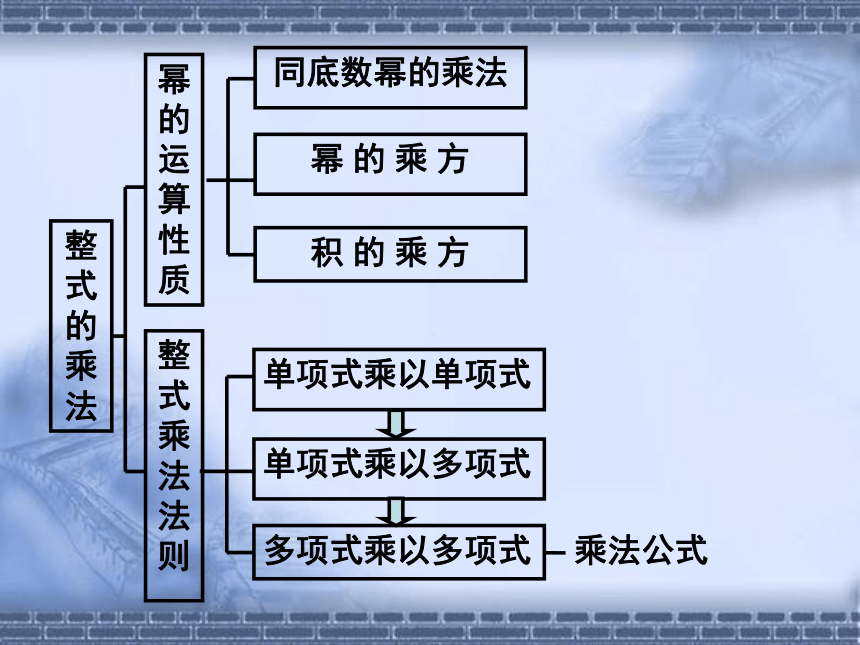
幂的运算性质
同底数幂的乘法
幂 的 乘 方
积 的 乘 方
乘法公式
整式的乘法
整式乘法法则
单项式乘以单项式
单项式乘以多项式
多项式乘以多项式
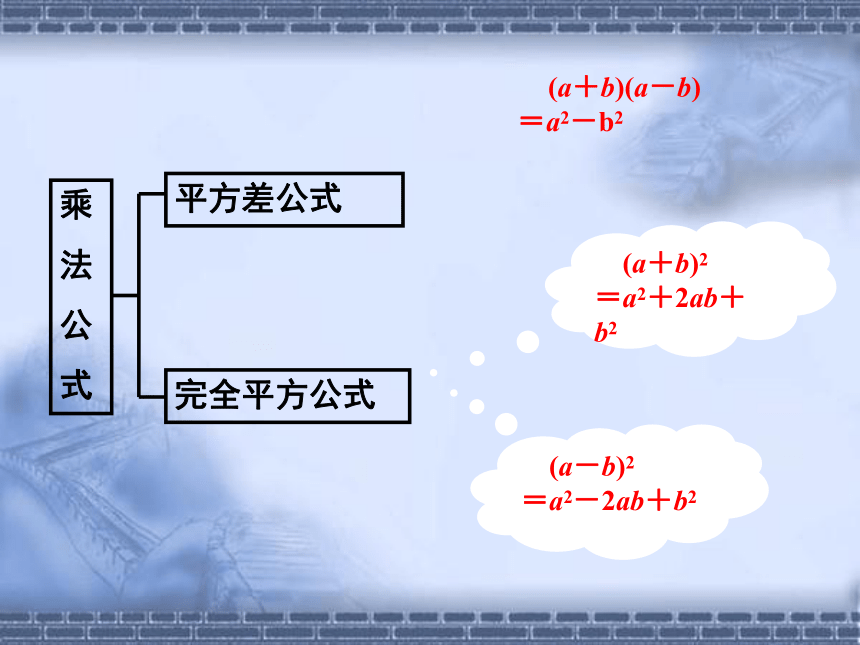
乘
法
公
式
平方差公式
完全平方公式
(a+b)(a-b)=a2-b2
(a+b)2
=a2+2ab+b2
(a-b)2
=a2-2ab+b2
① a2a3a =a5
② (m2)4=m
③ -( b)2 =2b2
④ (-5a2b2)(-3ab3 )=15a3b5
练习 辨析下面各式计算的对错.
1
错
正确答案: a6
6
6
错
正确答案: m8
错
-2
正确答案:- 4b2
c
c
错
正确答案:15a3b5c
-2
⑦ (-3x-2)(3x-2) =4-9x2
⑤ -m2(2m2 3mn )=-2m4-3m3n
⑥ 2n3 3n3=6n6
⑧ (2x-3y)2=4x2 xy + 9y2
-1
-
错
正确答案:-2m4+3m3n+m2
+
+
错
正确答案: 5n3
对
-6
-6
错
正确答案: 4x2-12xy + 9y2
-
-1
例1 ①已知:x2-4=0
求代数式 x(x+1)2-x(x2+x)-x-7的值.
②已知(2a+2b+1) (2a+2b-1)=63
求a+b的值.
x的值不必求出,把x2直接代入计算更简单
①解:原式=x(x2+2x+1 ) -x3-x2-x-7
=x3+2x2+x-x3-x2-x-7
=
∵ x2-4=0
∴ x2=4
∴ 原式=4-7=-3
x2-7
例1 ①已知:x2-4=0
求代数式 x(x+1)2-x(x2+x)-x-7的值.
②已知(2a+2b+1) (2a+2b-1)=63
求a+b的值.
②解:∵(2a+2b+1)(2a+2b-1)=63
∴ [(2a+2b)+1] [(2a+2b)-1]=63
∴ (2a+2b)2-1=63
∴ 4(a+b)2=64
∴ (a+b)2=16
由平方根的意义可得a+b=±4
本题由条件不能直接得出a、b的值,
把(a+b)看成一个整体来处理.
(x+100-3000 ) ( y-2 ) =(x-3000)y-1400
某商场将每台进价为3000元的彩电以x元的销售价售出,每天可售出y台.这种品牌的彩电如果每台降价100元,每天可多售出3台,多获利1800元.如果每台涨价100元,每天则少售出2台,少获利1400元.则原来每天的销售利润是多少?
例2
解:根据题意得:
(x-100-3000 ) ( y+3 ) =(x-3000)y+1800
(3900-3000)×6=5400
答:原来每天的销售利润是5400元.
解:根据题意得:
(x-100-3000 ) ( y+3 ) =(x-3000)y+1800
(x+100-3000 ) ( y-2 ) =(x-3000)y-1400
化简得:
3x-100y=11100
2x-100y=7200
解得:
x=3900
y=6
变形为:
xy + 3x -3100y - 9300=xy-3000y+1800
xy - 2x -2900y + 5800=xy-3000y-1400
例3 已知 xa=2,xb=3, 求xa+b的值.
解:∵ xa=2,xb=3
∴ xa+b= xa· xb=2×3 = 6.
变式:已知 xa+b =6, xb=3,求 xa 的值.
延伸:已知 xa=2,xb=3, 求x2a+3b的值.
解:∵ xa=2,xb=3
∴ x2a+3b= x2a· x3b
=(xa )2 ·(xb)3
=22×33
= 108.
xa+b=xa·xb
x2a+3b= x2a· x3b
(xa )2
(xb)3
拓展:已知am =2,bm =5,求 ( a3b2)m的值.
解:∵ am =2,bm =5,
∴ (a3b2)m
=a3m · b2m
= (am)3 · (bm)2
=23×52
=200
( a3b2)m
=a3mb2m
a3m=(am)3
b2m= (bm)2
如图所示的图形是用4个 相同的小矩形与1个小正方形镶嵌而成的正方形图案,用x,y表示小矩形的两边长(x>y).观察图形,思考代数式(x+y)2, (x-y)2, xy在图形中表示的意义.
例4
(x-y)2= (x+y)2 -4xy .
验证:运用所学知识验证关系式
(x-y)2= (x+y)2-4xy .
证明:∵ (x-y)2=x2-2xy+y2
(x+y)2-4xy=x2+2xy+y2 -4xy
=x2-2xy+y2
∴ (x-y)2= (x+y)2-4xy
根据上述关系,已知
x+y,x-y,xy这三个量中的任意两个量,可求出第三个量.
应用: 已知:x+y=7,xy=6
求:x2-y2的值.
分析:(x+y)(x-y) = x2-y2
已知
?
(x-y)2= (x+y)2 -4xy
解:∵ (x+y)2=(x-y)2+4xy
x+y=7, xy=6
∴ 72=(x-y)2+4×6
∴ (x-y)2=25
∴ x-y=±5
∵ x > y
∴ x-y=5
∴ x2-y2=7×5=35 .
应用: 已知:x+y=7,xy=6
求:x2-y2的值.
学法指导
在进行整式运算时,首先要正确把握运算顺序.在每一步的运算中,要看清运算类型,正确运用运算性质和法则.计算过程中,要时刻注意符号;
2. 乘法公式是本节的重点和难点,是计算和
化简求值的重要工具,对公式及其之间的
关系要清晰理解;
3. 各种运算性质和法则要能从正反两方面来
理解,会灵活运用;
4. 在解题时要注意结合题目条件和目标,从
整体上去考虑问题.
目标导引
掌握正整数幂的运算性质,并能应用性质 熟练地进行运算.
2. 掌握整式乘法的运算法则,并会运用法则
进行简单的整式乘法运算.
能灵活运用平方差公式与完全平方公式进 行计算.
4. 能运用整式的乘法解决一些数学问题和实
际问题.体验整式乘法在数学变形中的重
要作用.
幂的运算性质
同底数幂的乘法
幂 的 乘 方
积 的 乘 方
乘法公式
整式的乘法
整式乘法法则
单项式乘以单项式
单项式乘以多项式
多项式乘以多项式
幂的运算性质
同底数幂的乘法
幂 的 乘 方
积 的 乘 方
aman=am+n
(m、n为正整数 )
(am)n=amn
(m、n为正整数 )
(ab)m=ambn
(m,n为正整数 )
幂的运算性质
同底数幂的乘法
幂 的 乘 方
积 的 乘 方
乘法公式
整式的乘法
整式乘法法则
单项式乘以单项式
单项式乘以多项式
多项式乘以多项式
乘
法
公
式
平方差公式
完全平方公式
(a+b)(a-b)=a2-b2
(a+b)2
=a2+2ab+b2
(a-b)2
=a2-2ab+b2
① a2a3a =a5
② (m2)4=m
③ -( b)2 =2b2
④ (-5a2b2)(-3ab3 )=15a3b5
练习 辨析下面各式计算的对错.
1
错
正确答案: a6
6
6
错
正确答案: m8
错
-2
正确答案:- 4b2
c
c
错
正确答案:15a3b5c
-2
⑦ (-3x-2)(3x-2) =4-9x2
⑤ -m2(2m2 3mn )=-2m4-3m3n
⑥ 2n3 3n3=6n6
⑧ (2x-3y)2=4x2 xy + 9y2
-1
-
错
正确答案:-2m4+3m3n+m2
+
+
错
正确答案: 5n3
对
-6
-6
错
正确答案: 4x2-12xy + 9y2
-
-1
例1 ①已知:x2-4=0
求代数式 x(x+1)2-x(x2+x)-x-7的值.
②已知(2a+2b+1) (2a+2b-1)=63
求a+b的值.
x的值不必求出,把x2直接代入计算更简单
①解:原式=x(x2+2x+1 ) -x3-x2-x-7
=x3+2x2+x-x3-x2-x-7
=
∵ x2-4=0
∴ x2=4
∴ 原式=4-7=-3
x2-7
例1 ①已知:x2-4=0
求代数式 x(x+1)2-x(x2+x)-x-7的值.
②已知(2a+2b+1) (2a+2b-1)=63
求a+b的值.
②解:∵(2a+2b+1)(2a+2b-1)=63
∴ [(2a+2b)+1] [(2a+2b)-1]=63
∴ (2a+2b)2-1=63
∴ 4(a+b)2=64
∴ (a+b)2=16
由平方根的意义可得a+b=±4
本题由条件不能直接得出a、b的值,
把(a+b)看成一个整体来处理.
(x+100-3000 ) ( y-2 ) =(x-3000)y-1400
某商场将每台进价为3000元的彩电以x元的销售价售出,每天可售出y台.这种品牌的彩电如果每台降价100元,每天可多售出3台,多获利1800元.如果每台涨价100元,每天则少售出2台,少获利1400元.则原来每天的销售利润是多少?
例2
解:根据题意得:
(x-100-3000 ) ( y+3 ) =(x-3000)y+1800
(3900-3000)×6=5400
答:原来每天的销售利润是5400元.
解:根据题意得:
(x-100-3000 ) ( y+3 ) =(x-3000)y+1800
(x+100-3000 ) ( y-2 ) =(x-3000)y-1400
化简得:
3x-100y=11100
2x-100y=7200
解得:
x=3900
y=6
变形为:
xy + 3x -3100y - 9300=xy-3000y+1800
xy - 2x -2900y + 5800=xy-3000y-1400
例3 已知 xa=2,xb=3, 求xa+b的值.
解:∵ xa=2,xb=3
∴ xa+b= xa· xb=2×3 = 6.
变式:已知 xa+b =6, xb=3,求 xa 的值.
延伸:已知 xa=2,xb=3, 求x2a+3b的值.
解:∵ xa=2,xb=3
∴ x2a+3b= x2a· x3b
=(xa )2 ·(xb)3
=22×33
= 108.
xa+b=xa·xb
x2a+3b= x2a· x3b
(xa )2
(xb)3
拓展:已知am =2,bm =5,求 ( a3b2)m的值.
解:∵ am =2,bm =5,
∴ (a3b2)m
=a3m · b2m
= (am)3 · (bm)2
=23×52
=200
( a3b2)m
=a3mb2m
a3m=(am)3
b2m= (bm)2
如图所示的图形是用4个 相同的小矩形与1个小正方形镶嵌而成的正方形图案,用x,y表示小矩形的两边长(x>y).观察图形,思考代数式(x+y)2, (x-y)2, xy在图形中表示的意义.
例4
(x-y)2= (x+y)2 -4xy .
验证:运用所学知识验证关系式
(x-y)2= (x+y)2-4xy .
证明:∵ (x-y)2=x2-2xy+y2
(x+y)2-4xy=x2+2xy+y2 -4xy
=x2-2xy+y2
∴ (x-y)2= (x+y)2-4xy
根据上述关系,已知
x+y,x-y,xy这三个量中的任意两个量,可求出第三个量.
应用: 已知:x+y=7,xy=6
求:x2-y2的值.
分析:(x+y)(x-y) = x2-y2
已知
?
(x-y)2= (x+y)2 -4xy
解:∵ (x+y)2=(x-y)2+4xy
x+y=7, xy=6
∴ 72=(x-y)2+4×6
∴ (x-y)2=25
∴ x-y=±5
∵ x > y
∴ x-y=5
∴ x2-y2=7×5=35 .
应用: 已知:x+y=7,xy=6
求:x2-y2的值.
学法指导
在进行整式运算时,首先要正确把握运算顺序.在每一步的运算中,要看清运算类型,正确运用运算性质和法则.计算过程中,要时刻注意符号;
2. 乘法公式是本节的重点和难点,是计算和
化简求值的重要工具,对公式及其之间的
关系要清晰理解;
3. 各种运算性质和法则要能从正反两方面来
理解,会灵活运用;
4. 在解题时要注意结合题目条件和目标,从
整体上去考虑问题.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
