北师大版八年级数学下册2.1不等关系 (1)(共25张PPT)
文档属性
| 名称 | 北师大版八年级数学下册2.1不等关系 (1)(共25张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 915.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-16 10:49:01 | ||
图片预览






文档简介
第二章 一元一次不等式与 一元一次不等式组
2.1 不等关系
温故知新:
我们学过等式,请问什么是等式?
表示相等关系的式子叫等式。
我们知道相等关系的量可以利用等式来描述;同时,现实生活中还存在许多反映不等关系的量。比如,研究表明同学们每天睡觉的时间要不少于9小时;体育考试中合格的分数要不低于60分。请同学们也举一些不等关系的例子。
警告!为了你的生命安全,燃放时请及时转移至5米之外.
不相等 处处可见
从今天起,我们开始学习一类新的数学知识-----不等式和不等式组.
地球上海洋的面积大于陆地的面积,铅球的质量比篮球的质量大… …
利用相等关系可以解决许多问题,利用不等关系同样可以解决许多问题.在我们的生活中,不等关系更为普遍.
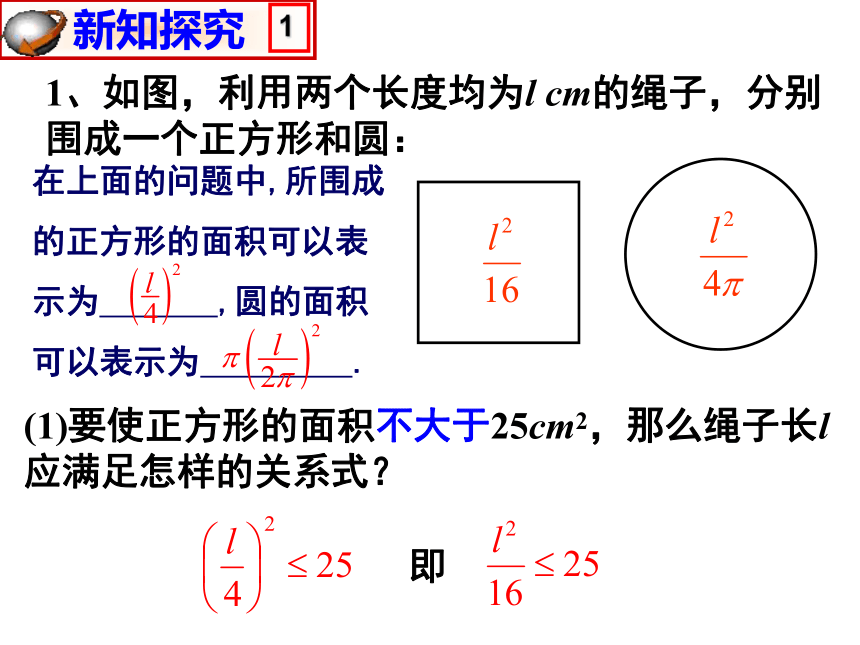
1、如图,利用两个长度均为l cm的绳子,分别围成一个正方形和圆:
(1)要使正方形的面积不大于25cm2,那么绳子长l应满足怎样的关系式?
在上面的问题中,所围成的正方形的面积可以表示为 ,圆的面积可以表示为 .
即
1
新知探究
1、如图,利用两个长度均为lcm的绳子,分别围成一个正方形和圆:
(2)如果要使圆的面积不小于100cm2,那么绳子长l应满足怎样的关系式?
即
1
新知探究
1、如图,利用两个长度均为lcm的绳子,分别围成一个正方形和圆:
(3)当l=8时,正方形和圆的面积哪个大?
∵4< 5.1
∴S正方形<S圆
1
新知探究
Ⅰ、如图,利用两个长度均为lcm的绳子,分别围
成一个正方形和圆:
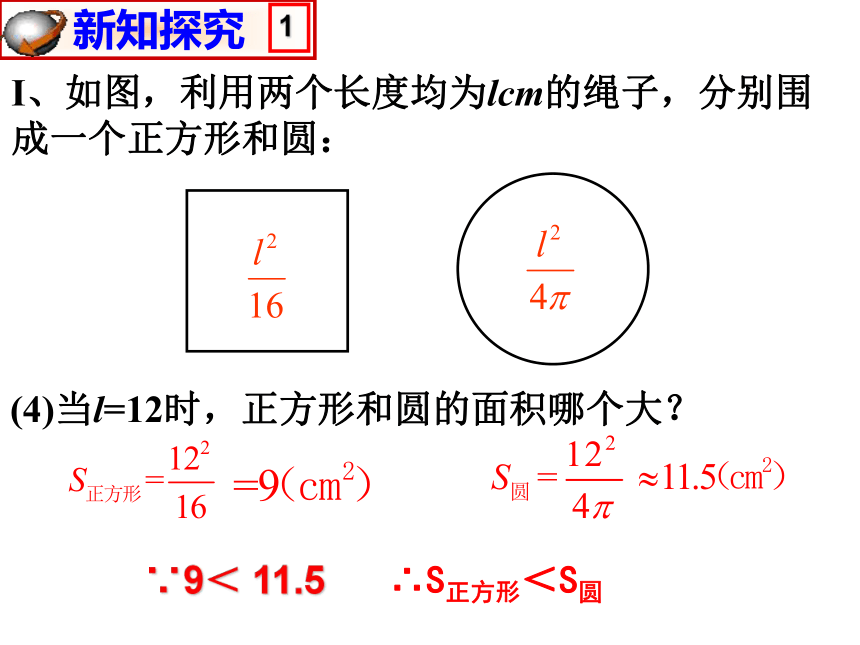
(4)当l=12时,正方形和圆的面积哪个大?
∵9< 11.5
∴S正方形<S圆
1
新知探究
Ⅰ、如图,利用两个长度均为lcm的绳子,分别围
成一个正方形和圆:
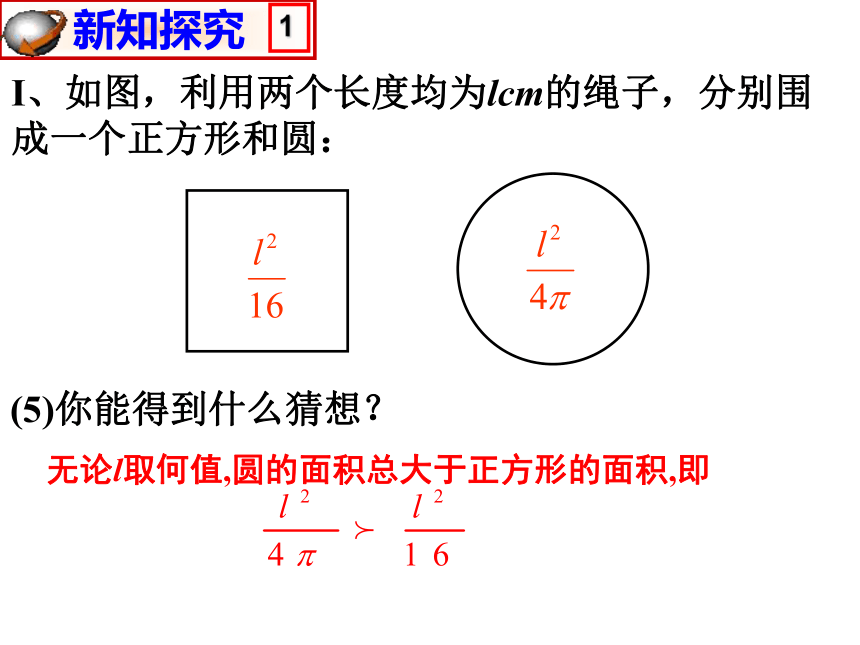
(5)你能得到什么猜想?
无论l取何值,圆的面积总大于正方形的面积,即
1
新知探究
2、通过测量一棵树的树围(树干的周长)可以计算它的树龄。通常以树干离地面1.5m的地方作为测量部位。某棵树栽种时的树围为5cm,以后树围每年约增加3cm,这棵树至少生长多少年其树围才能超过2.4m?(只列关系式)
2
新知探究
解:设这棵树生长x年其树围才能超过2.4m, 根据题意得:
5+3x>240
(1)、观察下列关系式,你有什么发现?
它们都是用不等号连接而成的式子
5+3x>240
1
合作交流
一 般地,用符号“<”(或“≤”),“>”(或“≥”) 连接的式子叫做不等式。
注意:
1、不等式表示代数式之间的不等关系;
2、判断一个式子是否是不等式,关键看所给式子是否含有不等号;
3、不等号有>、≥、<、≤、≠五种;
1
归纳新知
5+3x>240
1
例题解析
【例1】判断下列各式哪些是等式,哪些是不等式,哪些既不是等式又不是不等式.
①x+y ②3x>7 ③5=2x+3 ④x2≥0
⑤2x=3y=1 ⑥41 ⑦x=3 ⑧3>0
⑨x≠y-2
解:等式有③⑤⑦,
不等式有②④⑧⑨,
既不是等式又不是不等式的有①⑥。
【例2】用适当的符号表示下列关系:
(1)x的3倍与8的和比x的5倍小;
(2)x2是非负数;
(3)地球上海洋的面积大于陆地面积;
(4)老师的年龄不超过你的年龄的2倍。
解:
2
例题解析
(1) 3x+8<5x
(2) x2≥0
(3) 设地球上海洋面积为S海,陆地面积为S陆,
则S海>S陆
(4) 设老师的年龄为x, 你的年龄为y,
则x≤2y
关键词语
表明数量的不等关系
不等号
①大于
②比…大
③超过
①小于
②比…小
③低于
①不大于
②不超过
③至多
④最多
①不小于
②不低于
③至少
④最少
≥
>
<
≤
文字语言
表明数量的范围特征
符号 语言
a是正数
a是负数
a是非负数
a是非正数
a≤0
a>0
a<0
a≥0
【例3】甲、乙两种原料配制成某种饮料,已知这两种原料的维生素C含量及购买这两种原料的价如下表:
甲种原料
乙种原料
维生素C/(单位/千克)
600
100
原料价格/(元/千克)
8
4
现配制这种饮料10千克,要求至少含有4200单位
的维生素C,试写出所需甲种原料的质量x(千克)
应满足的不等式.
原料
维生素及价格
3
例题解析
600x+100(10-x) ≥4200
如果要求购买甲、乙两种原料的费用不超过72元,那么你能写出所需甲种原料的质量x(千克)应满足的另一个不等式吗?
8x+4(10-x) ≤72
随堂练习
1、用适当的符号表示下列关系:
(1)a是非负数;
(2)直角三角形斜边c比它的两直角边a,b都长;
(3)x与17的和比它的5倍小。
(4)两数的平方和不小于这两数积的2倍。
a≥0
c>a且c>b
x+17<5x
x2+y2≥2xy
2、表达式①x2≥0;②2a+4b≠3;③5m+2n;④x+y<0;⑤3x+2=9中的不等式有______________
(填序号)。
3、801班班长拿了56元钱去给班内20名优秀学生买奖品,奖品有两种:钢笔和笔记本。已知钢笔每支5元,笔记本每本3元,如果买x支钢笔,则列出关于x的不等式是 。
4、某厂今年的产值为100万元,预计明后两年平均每年增长率为x%,如果按此速度发展,后年该厂产值将超过a万元,请用不等式表示a与x的关系式是____
① ② ④
5x+3(20-x)≤56
100(1+x%)2>a
1、不等式的定义:
一般地,用符号“<”(或“≤”),“>”(或“≥”) 连接的式子叫做不等式。
2、“≥、≤”的意义:
(1)“≥”:a不小于(不低过)b,表示为a≥b ,
a为非负数表示为a≥0 ;
(2)“≤”:a不大于(不高过)b,表示为a≤b ,
a为非正数表示为a≤0 。
1
归纳总结
1. “不大于” 指的是 “ ”,
通常用符号 “ ” 表示。
“不小于”指的是“ ”,通常用符号
“ ”表示, 读作:“ ”.
小于或等于
≤
2. x 不大于10 可以表示为 ,
读作: .
x≤10
“x小于或等于10”
大于或等于
≥
大于或等于
1
反馈练习
4.从1、3、5、7、9中任取两个数就组成一组数,写出其中两数之和小于10的所有数组 .
1与3,1与5,1与7,3与5
1、用“<”或“>”号填空:
(1) -7____-5; (2) (-3)4____34;
(3) (-4)2____(-3)2; (4) |-0.5|____|-1000|;
(5) 3+4____1+4; (6) 5+3____12-5;
(7) 6×3____4×3; (8) 6×(-3)____4×(-3)
<
=
>
<
>
>
>
<
2
反馈练习
2、用适当的符号表示下列关系:
(1) a是负数;
(2) a是非负数;
(3) a与b的和小于5;
(4) a与b的平方和比a大;
(5) x的4倍不大于7;
(6) y的一半不小于3.
(7)直角三角形斜边c比它的两直角边a、b都长;
a<0
a≥0
a+b<5
4x≤7
y ≥3
c>a,c>b
a2+b2>a
2
反馈练习
2、在通过桥洞时,我们往往会看到如图(1)所示
的标志,这是限制车高的标志。你知道通过该桥
洞的车高x(m)的范围吗?在通过桥面时,我们往
往会看到如图(2)所示的标志,这是限制车重的标
志。你知道通过该桥面的车重y(t)的范围吗?
(1)
(2)
10t
5m
1
联系拓广
1、请你设计不同的实际背景来表示下列不等式:
(1) (2)
x<5,
y<10
x≤5,
y≤10
0
a
b
1.a 、b两个实数在数轴上的对应点如图所示:
请找出图中的不等关系,并用不等式表示.
2
联系拓广
B
A
A
C
2.图中A 、B、C的大小关系为 .
B<A<C
2.1 不等关系
温故知新:
我们学过等式,请问什么是等式?
表示相等关系的式子叫等式。
我们知道相等关系的量可以利用等式来描述;同时,现实生活中还存在许多反映不等关系的量。比如,研究表明同学们每天睡觉的时间要不少于9小时;体育考试中合格的分数要不低于60分。请同学们也举一些不等关系的例子。
警告!为了你的生命安全,燃放时请及时转移至5米之外.
不相等 处处可见
从今天起,我们开始学习一类新的数学知识-----不等式和不等式组.
地球上海洋的面积大于陆地的面积,铅球的质量比篮球的质量大… …
利用相等关系可以解决许多问题,利用不等关系同样可以解决许多问题.在我们的生活中,不等关系更为普遍.
1、如图,利用两个长度均为l cm的绳子,分别围成一个正方形和圆:
(1)要使正方形的面积不大于25cm2,那么绳子长l应满足怎样的关系式?
在上面的问题中,所围成的正方形的面积可以表示为 ,圆的面积可以表示为 .
即
1
新知探究
1、如图,利用两个长度均为lcm的绳子,分别围成一个正方形和圆:
(2)如果要使圆的面积不小于100cm2,那么绳子长l应满足怎样的关系式?
即
1
新知探究
1、如图,利用两个长度均为lcm的绳子,分别围成一个正方形和圆:
(3)当l=8时,正方形和圆的面积哪个大?
∵4< 5.1
∴S正方形<S圆
1
新知探究
Ⅰ、如图,利用两个长度均为lcm的绳子,分别围
成一个正方形和圆:
(4)当l=12时,正方形和圆的面积哪个大?
∵9< 11.5
∴S正方形<S圆
1
新知探究
Ⅰ、如图,利用两个长度均为lcm的绳子,分别围
成一个正方形和圆:
(5)你能得到什么猜想?
无论l取何值,圆的面积总大于正方形的面积,即
1
新知探究
2、通过测量一棵树的树围(树干的周长)可以计算它的树龄。通常以树干离地面1.5m的地方作为测量部位。某棵树栽种时的树围为5cm,以后树围每年约增加3cm,这棵树至少生长多少年其树围才能超过2.4m?(只列关系式)
2
新知探究
解:设这棵树生长x年其树围才能超过2.4m, 根据题意得:
5+3x>240
(1)、观察下列关系式,你有什么发现?
它们都是用不等号连接而成的式子
5+3x>240
1
合作交流
一 般地,用符号“<”(或“≤”),“>”(或“≥”) 连接的式子叫做不等式。
注意:
1、不等式表示代数式之间的不等关系;
2、判断一个式子是否是不等式,关键看所给式子是否含有不等号;
3、不等号有>、≥、<、≤、≠五种;
1
归纳新知
5+3x>240
1
例题解析
【例1】判断下列各式哪些是等式,哪些是不等式,哪些既不是等式又不是不等式.
①x+y ②3x>7 ③5=2x+3 ④x2≥0
⑤2x=3y=1 ⑥41 ⑦x=3 ⑧3>0
⑨x≠y-2
解:等式有③⑤⑦,
不等式有②④⑧⑨,
既不是等式又不是不等式的有①⑥。
【例2】用适当的符号表示下列关系:
(1)x的3倍与8的和比x的5倍小;
(2)x2是非负数;
(3)地球上海洋的面积大于陆地面积;
(4)老师的年龄不超过你的年龄的2倍。
解:
2
例题解析
(1) 3x+8<5x
(2) x2≥0
(3) 设地球上海洋面积为S海,陆地面积为S陆,
则S海>S陆
(4) 设老师的年龄为x, 你的年龄为y,
则x≤2y
关键词语
表明数量的不等关系
不等号
①大于
②比…大
③超过
①小于
②比…小
③低于
①不大于
②不超过
③至多
④最多
①不小于
②不低于
③至少
④最少
≥
>
<
≤
文字语言
表明数量的范围特征
符号 语言
a是正数
a是负数
a是非负数
a是非正数
a≤0
a>0
a<0
a≥0
【例3】甲、乙两种原料配制成某种饮料,已知这两种原料的维生素C含量及购买这两种原料的价如下表:
甲种原料
乙种原料
维生素C/(单位/千克)
600
100
原料价格/(元/千克)
8
4
现配制这种饮料10千克,要求至少含有4200单位
的维生素C,试写出所需甲种原料的质量x(千克)
应满足的不等式.
原料
维生素及价格
3
例题解析
600x+100(10-x) ≥4200
如果要求购买甲、乙两种原料的费用不超过72元,那么你能写出所需甲种原料的质量x(千克)应满足的另一个不等式吗?
8x+4(10-x) ≤72
随堂练习
1、用适当的符号表示下列关系:
(1)a是非负数;
(2)直角三角形斜边c比它的两直角边a,b都长;
(3)x与17的和比它的5倍小。
(4)两数的平方和不小于这两数积的2倍。
a≥0
c>a且c>b
x+17<5x
x2+y2≥2xy
2、表达式①x2≥0;②2a+4b≠3;③5m+2n;④x+y<0;⑤3x+2=9中的不等式有______________
(填序号)。
3、801班班长拿了56元钱去给班内20名优秀学生买奖品,奖品有两种:钢笔和笔记本。已知钢笔每支5元,笔记本每本3元,如果买x支钢笔,则列出关于x的不等式是 。
4、某厂今年的产值为100万元,预计明后两年平均每年增长率为x%,如果按此速度发展,后年该厂产值将超过a万元,请用不等式表示a与x的关系式是____
① ② ④
5x+3(20-x)≤56
100(1+x%)2>a
1、不等式的定义:
一般地,用符号“<”(或“≤”),“>”(或“≥”) 连接的式子叫做不等式。
2、“≥、≤”的意义:
(1)“≥”:a不小于(不低过)b,表示为a≥b ,
a为非负数表示为a≥0 ;
(2)“≤”:a不大于(不高过)b,表示为a≤b ,
a为非正数表示为a≤0 。
1
归纳总结
1. “不大于” 指的是 “ ”,
通常用符号 “ ” 表示。
“不小于”指的是“ ”,通常用符号
“ ”表示, 读作:“ ”.
小于或等于
≤
2. x 不大于10 可以表示为 ,
读作: .
x≤10
“x小于或等于10”
大于或等于
≥
大于或等于
1
反馈练习
4.从1、3、5、7、9中任取两个数就组成一组数,写出其中两数之和小于10的所有数组 .
1与3,1与5,1与7,3与5
1、用“<”或“>”号填空:
(1) -7____-5; (2) (-3)4____34;
(3) (-4)2____(-3)2; (4) |-0.5|____|-1000|;
(5) 3+4____1+4; (6) 5+3____12-5;
(7) 6×3____4×3; (8) 6×(-3)____4×(-3)
<
=
>
<
>
>
>
<
2
反馈练习
2、用适当的符号表示下列关系:
(1) a是负数;
(2) a是非负数;
(3) a与b的和小于5;
(4) a与b的平方和比a大;
(5) x的4倍不大于7;
(6) y的一半不小于3.
(7)直角三角形斜边c比它的两直角边a、b都长;
a<0
a≥0
a+b<5
4x≤7
y ≥3
c>a,c>b
a2+b2>a
2
反馈练习
2、在通过桥洞时,我们往往会看到如图(1)所示
的标志,这是限制车高的标志。你知道通过该桥
洞的车高x(m)的范围吗?在通过桥面时,我们往
往会看到如图(2)所示的标志,这是限制车重的标
志。你知道通过该桥面的车重y(t)的范围吗?
(1)
(2)
10t
5m
1
联系拓广
1、请你设计不同的实际背景来表示下列不等式:
(1) (2)
x<5,
y<10
x≤5,
y≤10
0
a
b
1.a 、b两个实数在数轴上的对应点如图所示:
请找出图中的不等关系,并用不等式表示.
2
联系拓广
B
A
A
C
2.图中A 、B、C的大小关系为 .
B<A<C
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
